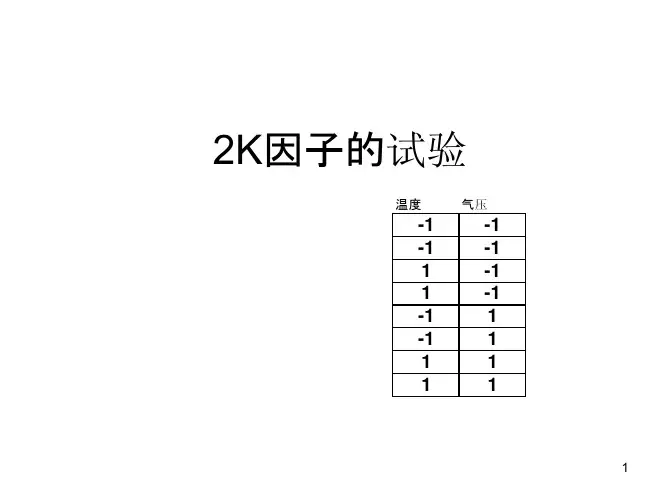
2K因子实验设计
- 格式:ppt
- 大小:1.77 MB
- 文档页数:58


2k因子实验设计简介一、引言2k因子实验设计是一种常用的实验设计方法,用于研究多个影响因素对实验结果的影响。
其中的2表示每个因素有两个水平,k表示有k个因素。
本文将对2k因子实验设计进行简要介绍。
二、2k因子实验设计的基本思想2k因子实验设计的基本思想是通过系统地改变若干个因素的水平,观察实验结果的变化,从而分析各个因素对结果的影响,并确定最优的因素组合。
其中,每个因素的水平通常选取两个,即高水平和低水平。
通过对所有可能的因素组合进行实验,可以得到全面而准确的数据,从而进行因素分析和优化。
三、2k因子实验设计的步骤1. 确定影响因素:首先需要确定影响实验结果的各个因素,这些因素可以是实验条件、操作参数或其他相关变量。
2. 确定因素水平:确定每个因素的水平,通常选取两个水平,即高水平和低水平。
3. 构建试验设计表:根据因素个数确定试验设计表的大小,并按照2k因子实验设计的原则填写试验设计表。
试验设计表中的每一行代表一个试验,列代表各个因素及其水平。
4. 进行实验:根据试验设计表进行实验,记录各个因素水平下的实验结果。
5. 分析数据:对实验结果进行统计分析,包括方差分析、回归分析等,以确定各个因素对结果的影响程度。
6. 优化因素组合:根据分析结果确定最优的因素组合,以达到最佳的实验效果。
四、2k因子实验设计的优点1. 高效性:2k因子实验设计可以同时研究多个因素,通过少量试验即可获取全面的数据。
2. 灵活性:可以根据实际需求选择不同的因素和水平进行设计,适用于各种不同的实验场景。
3. 可靠性:通过统计分析方法,可以准确地评估各个因素对结果的影响程度,提高实验结果的可靠性。
4. 可解释性:2k因子实验设计的结果可以直观地展示各个因素对结果的影响,便于解释和理解。
五、2k因子实验设计的应用领域2k因子实验设计广泛应用于工程、制造、医药、化工等领域。
例如,在工程领域中,可以利用2k因子实验设计来研究各个因素对产品性能的影响,以优化产品设计;在医药领域中,可以利用2k因子实验设计来研究药物各个因素对治疗效果的影响,以优化药物配方。

当有必要研究多因子对一反应变量的综合效果时,因子设计(Factorial Design)大量且普遍地应用于多因子的实验。
一最重要的情况是k个因子且各有2水准的状况(2k, Level Factor),此设计的完整反复需要2⨯2⨯…⨯2= 2k个观测值,且称之为2k因子设计(2k Factorial Design)。
本章重点将聚于此设计,另整章假设(1) 因子是固定的,(2) 设计是完全随机的,与(3) 一般的常态假设是满足的。
2k设计在实验工作的初期阶段,即当似乎有很多因子要研究时,是特别有效。
它提供了在一次完整因子设计里可以研究k个因子的最小次数。
因此,此种设计是大量应用于因子筛选实验(Factor Screening Experiments)。
因为每个因子只有2个水准,假设反应在选定的因子水准范围里是近似线性的,在很多因子筛选实验中,刚开始研究过(制)程或系统时,此假设是合理的。
6-22k设计(The 2k Design)在2k系列中首先讨论2个因子(22),A与B,各有2水准,此称之为22因子设计,因子水准可称之为”低”与”高”。
如,有一反应浓度和触媒量对化学反应过(制)程合格率效果的研究,令反应浓度为因子A,且有兴趣的2水准为15%与20%;另触媒量为因子B,且高水平为2 lbs与低水准为1 lb,实验反复3次,资料如下,图6-1 22设计之处理组合设计中的4个处理组合通常以小写字母表示,由上图知,在处理组合中任何因子的高水平以对应小写字母表示;处理组合中任何因子的低水准以对应字母的不出现表示。
依传统,(1)表示2因子都是在低水准,这个记号在整个2k系统都适用。
在22因子设计中,定义一个因子的平均效果为该因子水准改变所带来的反应改变。
同时,符号(1)、a、b、ab表示在处理组合下n次反复的总和,则在B为低水准时A的效果为[a-(1)]/n与在B为高水平时A的效果为[ab-b]/n,将此两者取平均即为A的主效果(Main Effect):A = {[a-(1)] + [ab-b]}/2nA = [ab + a - b - (1)]/2n (6-1)同理,B的主效果,即在A为低水准时B的效果为[b-(1)]/n 与在A为高水平时B的效果为[ab-a]/n,将此两者取平均,则为B = {[b-(1)] + [ab-a]}/2nB = [ab + b - a - (1)]/2n (6-2)定义交互作用(Interaction Effect) AB为B在高水平时A 的效果与B在低水准时A的效果间的平均差异,AB = {[ab-b]-[a-(1)]}/2n= [ab+ (1) - a - b]/2n (6-3)亦可定义AB 为A 在高水平时B 的效果与A 在低水准时B 的效果间的平均差异,其结果与式(6-3)同。