高考试题分类——集合 04-07

圆学子梦想铸金字品牌1.（ 2013 ·重庆高考文科·Ｔ 1）已知全集U1,2,3,4 ，集合 A1,2 ,B2,3 ，则 C U A B()A ．1,3,4 B.3,4 C.3 D.42、（ 2013 ·四川高考文科·Ｔ 1）设集合A{1,2,3} ，集合 B {2,2} ，则A I B（）A. B. {2} C. {2,2} D. {2,1,2,3}3.(2013 ·福建高考文科·T3) 若集合A=1,2,3 ，B= 1,3,4 ，,则A∩B的子集个数为()A.2B.3C.4D.164.（ 2013 ·湖北高考文科·Ｔ 1）已知全集U{1,2,3,4,5} ，集合A{1,2} ， B{2,3,4}，则 B C u A （）A． {2} B ． {3,4}C． {1,4,5} D ． {2,3,4,5}5.（ 2013 ·新课标Ⅰ高考文科·Ｔ 1）已知集合A{1,2,3,4} ， B{ x | x n2 , n A} ,则A∩B=A. {1,4}B. { 2,3}C.{ 9,16}D. {1,2}6.（ 2013 ·大纲版全国卷高考文科·Ｔ 1）设集合U1,2,3,4,5,集合A1,2 ,e u A（）则C U AA.1,2B.3,4,5C.1,2,3,4,5D.7.（ 2013 ·湖南高考文科）已知集合 U{2,3,6,8},A{2,3}, B{2,6,8},则(C U A)B________8.设集合A1,2,3 , B4,5, M x | x a b, a A, b B, 则 M 中元素的个数为（）A.3B.4C.5D.69. (2013 江·苏高考数学科·T4) 集合 {-1,0,1} 共有个子集 .10.（ 2013 ·四川高考理科·Ｔ 1）设集合A{ x | x20} ，集合 B { x | x240} ，则AI B（）A. {2}B. {2}C. { 2,2}D.11.(2013 浙·江高考文科·T1) 设集合 S={x|x>-2},T={x|- 4≤ x≤ 1},则 S∩ T= ()A.[- 4,+ ∞)B.(- 2,+ ∞ )C.[ -4,1]D.(-2,1]12.（ 2013 ·安徽高考文科·Ｔ2）已知A= ｛ x|x+1>0 ｝， B= ｛ -2， -1， 0， 1｝，则（ C 错误!未找到引用源。

2023年高考数学试题分类解析【第一章集合与常用逻辑用语】第一节集合1.（2023全国甲卷理科1）设集合{}31,A x x k k ==+∈Z ，{}32,B x x k k ==+∈Z ，U 为整数集，则()U A B = ð（）A.{}3,x x k k =∈Z B.{}31,x x k k =-∈Z C.{}32,x x k k =-∈Z D.∅【分析】根据整数集的分类，以及补集的运算即可解出．【解析】因为整数集{}{}{}3,3+1,3+2,x x k k x x k k x x k k ==∈=∈=∈Z Z Z Z ，=U Z ，所以(){}3,U A B x x k k ==∈Z ð．故选A．2.（2023全国甲卷文科1）设全集{}1,2,3,4,5U =，集合{}1,4M =，{}2,5N =，则U N M = ð（）A.{}2,3,5 B.{}1,3,4 C.{}1,2,4,5 D.{}2,3,4,5【分析】利用集合的交并补运算即可得解.【解析】因为全集{1,2,3,4,5}U =，集合{1,4}M =，所以{}2,3,5U M =ð，又{2,5}N =，所以{2,3,5}U N M = ð.故选A.3.（2023全国乙卷理科2）设集合U =R ，集合{}1M x x =<，{}12N x x =-<<，则{}2x x = （）A.()U M N ð B.U N Mð C.()U M N ð D.U M Nð【分析】由题意逐一考查所给的选项运算结果是否为{}2x x 即可.【解析】由题意可得{}2M N x x =< ，则(){}2U M N x x = ð ，选项A 正确；{}1U M x x =ð ，则{}1U N M x x =>- ð，选项B 错误；{}11M N x x =-<< ，则(){}11U M N x x x =- 或ð ，选项C 错误；{}12U N x x x =-或ð ，则{}12U M N x x x =< 或ð ，选项D 错误；故选A.4.（2023全国乙卷文科2）设全集{}0,1,2,4,6,8U =，集合{}0,4,6M =，{}0,1,6N =，则U M N = ð（）A.{}0,2,4,6,8 B.{}0,1,4,6,8 C.{}1,2,4,6,8 D.U【分析】由题意可得U N ð的值，然后计算U M N ð即可.【解析】由题意可得{}2,4,8U N =ð，则{}0,2,4,6,8U M N = ð.故选A.5.（2023新高考I 卷1）已知集合{}2,1,0,1,2M =--，{}260N x x x =--≥，则M N = （）A.{}2,1,0,1--B.{}0,1,2 C.{}2- D.{}2【解析】{}(][)260,23,N x x x =--≥=-∞-+∞ ，所以{}2M N =- ，故选C.6.（2023新高考II 卷2）2.设集合{}{}0,,1,2,22A a B a a =-=--，若A B ⊆，则a =（）A.2 B.1 C.23D.1-【解析】因为A B ⊆，所以必有20a -=或220a -=，解得2a =或1a =.当2a =时，{}{}0,2,1,0,2A B =-=，不满足A B ⊆；当1a =时，{}{}0,1,1,1,0A B =-=-，符合题意.所以1a =.故选B.7.（2023北京卷1）已知集合{}20M x x =+ ，{}10N x x =-<，则M N = （）A.{}21x x -<B.{}21x x -<C.{}2x x - D.{}1x x <【分析】先化简集合,M N ，然后根据交集的定义计算.【解析】由题意，{20}{|2}M xx x x =+≥=≥-∣，{10}{|1}N x x x x =-<=<∣，根据交集的运算可知，{|21}M N x x =-≤< .故选A.8.（2023天津卷1）已知集合{}{}{}1,2,3,4,5,1,3,1,2,4U A B ===，则U B A = ð（）A．{}1,3,5B．{}1,3C．{}1,2,4D．{}1,2,4,5【分析】对集合B 求补集，应用集合的并运算求结果；【解析】由{3,5}U B =ð，而{1,3}A =，所以{1,3,5}U B A = ð.故选A.第二节充分条件与必要条件、全称量词与存在量词1.（2023全国甲卷理科7）“22sin sin 1αβ+=”是“sin cos 0αβ+=”的（）A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【分析】根据充分条件、必要条件概念及同角三角函数的基本关系得解.【解析】当2απ=，0β=时，有22sin sin 1αβ+=，但sin cos 0αβ+≠，即22sin sin 1αβ+=推不出sin cos 0αβ+=；当sin cos 0αβ+=时，()2222sin sin cos sin 1αβββ+=-+=，即sin cos 0αβ+=能推出22sin sin 1αβ+=.综上可知，22sin sin 1αβ+=是sin cos 0αβ+=成立的必要不充分条件.故选B.2.（2023新高考I 卷7）已记n S 为数列{}n a 的前n 项和，设甲：{}n a 为等差数列；乙：n S n ⎧⎫⎨⎬⎩⎭为等差数列，则（）A.甲是乙的充分条件但不是必要条件B.甲是乙的必要条件但不是充分条件C.甲是乙的充要条件D.甲既不是乙的充分条件也不是乙的必要条件【解析】{}n a 为等差数列，设首项为1a 公差为d ，则()112n n n S na d -=+，111222n S n d d a d n a n -=+=+-，所以n S n ⎧⎫⎨⎬⎩⎭为等差数列，所以甲是乙的充分条件.n S n ⎧⎫⎨⎬⎩⎭为等差数列，即()()()1111111n n n n n n nS n S S S na S n n n n n n +++-+--==+++为常数，设为t ，即()11n nna S t n n +-=+，故()11n n S na tn n +=-+，()()()1112n n S n a t n n n -=---≥，两式相减得()1112n n n n n a S S na n a tn -+=-=---，12n n a a t +-=为常数，对1n =也成立，所以{}n a 为等差数列，所以甲是乙的必要条件.所以，甲是乙的充要条件，故选C.3.（2023北京卷8）若0xy ≠，则“0x y +=”是“2x yy x+=-”的（）A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【分析】解法一：证明充分性可由0x y +=得到x y =-，代入x yy x+化简即可，证明必要性可由2x y y x +=-去分母，再用完全平方公式即可；解法二：由x yy x+通分后用配凑法得到完全平方公式，证明充分性可把0x y +=代入即可；证明必要性把2x yy x+=-代入，解方程即可.【解析】解法一：充分性：因为0xy ≠，且0x y +=，所以x y =-，所以112x y y y y x y y-+=+=--=--，所以充分性成立；必要性：因为0xy ≠，且2x yy x+=-，所以222x y xy +=-，即2220x y xy ++=，即()20x y +=，所以0x y +=.所以必要性成立.所以“0x y +=”是“2x yy x+=-”的充要条件.故选C.解法二：充分性：因为0xy ≠，且0x y +=，所以()2222222222x y xy x y x y x y xy xy xy y x xy xy xy xy+-+++--+=====-，所以充分性成立；必要性：因为0xy ≠，且2x yy x+=-，所以()()22222222222x y xy x y x y x y x y xy xy y x xy xy xy xy+-++++-+====-=-，所以()20x y xy+=，所以()20x y +=，所以0x y +=，所以必要性成立.所以“0x y +=”是“2x yy x+=-”的充要条件.故选C.4.（2023天津卷2）“22a b =”是“222a b ab +=”的（）A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分又不必要条件【分析】根据充分、必要性定义判断条件的推出关系，即可得答案.【解析】由22a b =，则a b =±，当0a b =-≠时222a b ab +=不成立，充分性不成立；由222a b ab +=，则2()0a b -=，即a b =，显然22a b =成立，必要性成立；所以22a b =是222a b ab +=的必要不充分条件.故选B.。

新课标全国高考数学试题分类汇编一(集合、复数)(word版可编辑修改) 编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（新课标全国高考数学试题分类汇编一(集合、复数)(word版可编辑修改)）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为新课标全国高考数学试题分类汇编一(集合、复数)(word版可编辑修改)的全部内容。

新课标全国高考文科数学试题分类汇编一（集合、复数）2015—11．已知集合{32,},{6,8,10,12,14}A x x n n N B ==+∈=，则集合A B 中的元素个数为( ）（A) 5 （B)4 （C ）3 （D ）23．已知复数z 满足(1)1z i i -=+，则z =（ ）（A ） 2i -- （B ）2i -+ (C ）2i - （D)2i +2015—21．已知集合{}|12A x x =-<<，{}|03B x x =<<，则A B =( ）A ．()1,3-B ．()1,0-C ．()0,2D ．()2,32．若为a 实数,且231aii i +=++，则a =（ ）A ．4-B ．3-C ．3D ．42016-1(1)设集合{1,3,5,7}A =，{|25}B x x =≤≤，则A B =（ ）(A ）{1，3}（B ）{3，5}(C ）{5,7｝（D ）{1，7｝(2）设(12i)(i)a ++的实部与虚部相等，其中a 为实数,则a=（ ）(A)－3（B ）－2(C ）2（D ）32016-21、已知集合A={1,2,3}，B=｛x ｜x 2〈9}，则A∩B= （ )A ．{–2,–1，0，1,2，3}B ．{–2,–1,0,1,2｝C ．{1,2，3}D ．{1,2｝ 2、设复数z 满足z+i+3–i,则错误!=( ）A ．–1+2iB ．1–2iC ．3+2iD ．3–2i2016—3（1）设集合{0,2,4,6,8,10},{4,8}A B ==，则B C A =（ )（A ）{48}， （B ）{026}，， (C ）{02610}，，， （D ）{0246810}，，，，，（2)若43i z =+，则||zz =（ ）新课标全国高考数学试题分类汇编一(集合、复数)(word 版可编辑修改) (A ）1（B)1- (C ）43+i 55 （D ）43i 55-2017—1 1、已知集合A=｛x|x<2}，B={x|3–2x>0｝，则（ )A ．A ∩B={x|x<错误!｝B ．A ∩B =ΦC ．A ∪B={x|x 〈错误!}D ．A ∪B=R3、下列各式的运算结果为纯虚数的是（ )A ．i （1+i ）2B ．i 2(1–i)C ．(1+i ）2D ．i （1+i ）2017—21、设集合A=｛1,2,3}，B={2,3,4},则A∪B=( )A ．{1，2，3，4}B ．｛1,2，3｝C ．｛2，3,4｝D ．｛1,3，4｝2、（1+i)(2+i ）=（ )A ．1–iB ．1+3iC ．3+iD ．3+3i2017-31．已知集合A={1，2,3,4}，B={2，4,6，8}，则A ⋂B 中元素的个数为（ ）A ．1B ．2C ．3D ．4 2．复平面内表示复数z=i(–2+i)的点位于( ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限2018-11．已知集合{}02A =，，{}21012B =--，，，，，则A B =( ） A ．{}02，B ．{}12，C ．{}0D ．{}21012--，，，， 2．设1i 2i 1i z -=++，则z =（ ) A ．0B ．12 C ．1 D 2018-2 1．i(2+3i)=（ )A ．32i -B ．32i +C ．32i --D ．32i -+2．已知集合{}1,3,5,7A =，{}2,3,4,5B =则A B =( ）A ．{}3B ．{}5C ．{}3,5D ．{}1,2,3,4,5,72018-31．已知集合{|10}A x x =-≥，{0,1,2}B =,则A B =（ )新课标全国高考数学试题分类汇编一(集合、复数)(word版可编辑修改) A．{0}B．{1}C．{1,2}D．{0,1,2} 2．(1i)(2i)+-=( )A．3i-+C．3i-D．3i+ --B．3i。

高考集合考试题及答案第一部分：语文一、阅读理解高考人数增多，如何保证考试的公平性？面对这个问题，一种解决方案出现了：高考集合考试。

集合考试是指在全国范围内，所有考生在同一天同时进行考试，试卷内容完全相同。

通过这种方式，可以避免考生之间的信息传递和答案泄露，确保考试的公平性和公正性。

下面是一篇关于集合考试的报道，请仔细阅读并回答问题。

今年高考将首次进行全国范围内的集合考试，以下是部分考题和答案，供大家参考。

题目一：下列哪个选项与集合考试的目的最相符？A. 提高参与考试的学生数量B. 保证考试的难度与往年相同C. 确保考试过程的公平性D. 降低高考的难度，增加录取人数答案：C题目二：以下哪项是集合考试的优势？A. 跨区域竞争B. 高校录取数量增加C. 考生之间答案交流D. 杜绝作弊行为答案：D题目三：集合考试对考生和学校来说有哪些影响？A. 考生压力增大，学校录取难度增加B. 考生无压力，学校录取过程更加公平C. 考生无变化，学校录取数量增加D. 考生数量减少，学校选择余地增大答案：B题目四：集合考试的实施对教育改革有何作用？A. 促进教育公平B. 提高高校竞争力C. 减少考试压力D. 缩短教育周期答案：A二、写作请你根据以下提示，用不少于800字的篇幅，写一篇关于集合考试的短文。

提示：1. 简要描述集合考试的概念和目的；2. 分析集合考试对考生和学校的影响；3. 探讨集合考试对教育公平的促进作用；4. 你对集合考试的看法和建议。

（文章内容略，仅供参考）第二部分：数学一、选择题1. 已知a、b是两个正实数，且满足a/b=2，则下列哪个等式成立？A. 2a/b = 4B. a + b = 3a - bC. a - b = a/bD. (a+b)/(2a) = 1答案：C2. 已知正实数a、b满足2a = 3b，则下列哪个选项为真？A. a > bB. a < bC. a = bD. a + b = 0答案：A3. 下列哪个等式成立？A. (x+2)(x-2) = x^2 - 4B. x^2 + 4 = (x+2)(x-2)C. (x+2)(x-2) = x^2 + 4D. x^2 - 4 = 0答案：A二、解答题1. 解方程组：2x - y = 3x + y = 7解答：将第二个方程两边乘以2得：2x + 2y = 14将第一个方程与上述等式相加，消去y得：4x = 17因此，x = 17/4将x的值带入任意一个方程，求得y的值：17/4 + y = 7解得y = -1/4答案：x = 17/4，y = -1/42. 计算下列方程的解：2x^2 + 3x - 5 = 0解答：使用求根公式，即x = (-b ± √(b^2 - 4ac)) / 2a带入a = 2，b = 3，c = -5计算得两个解：x = 1，x = -2.5答案：x = 1，x = -2.5第三部分：英语一、完形填空（略）二、阅读理解阅读下面的短文，然后选择正确答案。

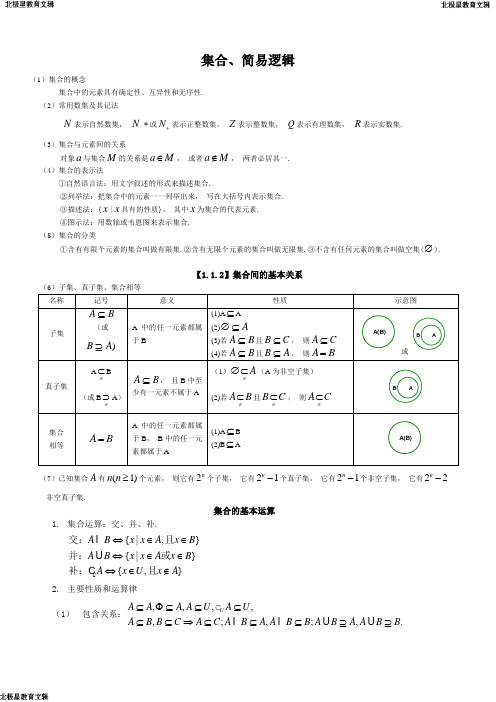
集合、简易逻辑（1）集合的概念集合中的元素具有确定性、互异性和无序性. （2）常用数集及其记法N 表示自然数集， N *或N +表示正整数集， Z 表示整数集， Q 表示有理数集， R 表示实数集.（3）集合与元素间的关系对象a 与集合M 的关系是a M ∈， 或者a M ∉， 两者必居其一. （4）集合的表示法①自然语言法：用文字叙述的形式来描述集合.②列举法：把集合中的元素一一列举出来， 写在大括号内表示集合. ③描述法：{x |x 具有的性质}， 其中x 为集合的代表元素. ④图示法：用数轴或韦恩图来表示集合. （5）集合的分类①含有有限个元素的集合叫做有限集.②含有无限个元素的集合叫做无限集.③不含有任何元素的集合叫做空集(∅).【1.1.2】集合间的基本关系（6）子集、真子集、集合相等 名称记号意义性质示意图子集B A ⊆（或)A B ⊇A 中的任一元素都属于B(1)A ⊆A(2)A ∅⊆(3)若B A ⊆且B C ⊆， 则A C ⊆ (4)若B A ⊆且B A ⊆， 则A B =A(B)或B A真子集A ≠⊂B（或B ≠⊃A ）B A ⊆， 且B 中至少有一元素不属于A（1）A ≠∅⊂（A 为非空子集）(2)若A B ≠⊂且B C ≠⊂， 则A C ≠⊂B A集合 相等A B =A 中的任一元素都属于B ， B 中的任一元素都属于A(1)A ⊆B (2)B ⊆AA(B)（7）已知集合A 有(1)n n ≥个元素， 则它有2n 个子集， 它有21n -个真子集， 它有21n -个非空子集， 它有22n -非空真子集.集合的基本运算1. 集合运算：交、并、补.{|,}{|}{,}A B x x A x B A B x x A x B A x U x A ⇔∈∈⇔∈∈⇔∈∉I U U 交：且并：或补：且C 2. 主要性质和运算律 （1） 包含关系：,,,,,;,;,.U A A A A U A U A B B C A C A B A A B B A B A A B B ⊆Φ⊆⊆⊆⊆⊆⇒⊆⊆⊆⊇⊇I I U U C原命题若p 则q 否命题若┐p 则┐q 逆命题若q 则p 逆否命题若┐q 则┐p 互为逆否互逆否互为逆否互互逆否互（2） 等价关系：U A B A B A A B B A B U ⊆⇔=⇔=⇔=I U U C （3） 集合的运算律：交换律：.;A B B A A B B A Y Y I I ==结合律:)()();()(C B A C B A C B A C B A Y Y Y Y I I I I == 分配律:.)()()();()()(C A B A C B A C A B A C B A Y I Y I Y I Y I Y I == 0-1律：,,,A A A U A A U A U Φ=ΦΦ===I U I U 等幂律：.,A A A A A A ==Y I求补律：A ∩C U A =φ A ∪C U A =U C U U =φ C U φ=U 反演律：C U (A ∩B)= (C U A )∪(C U B ) C U (A ∪B)= (C U A )∩(C U B )简易逻辑1、命题的定义：可以判断真假的语句叫做命题。

历年(2020-2024)全国高考数学真题分类(集合与常用逻辑用语)汇编考点01 集合间的基本关系1．（2023∙全国新Ⅱ卷∙高考真题）设集合{}0,A a =-，{}1,2,22B a a =--，若A B ⊆，则=a （ ）． A ．2 B ．1 C ．23 D ．1-2．（2020全国新Ⅰ卷∙高考真题）已知a ∈R ，若集合{}1,M a =，{}1,0,1N =-，则“0a =”是“M N ⊆”的（ ） A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件考点02 交集1．（2024∙全国新Ⅰ卷高考真题）已知集合{}355,{3,1,0,2,3}A xx B =-<<=--∣，则A B = （ ） A ．{1,0}- B ．{2,3} C ．{3,1,0}-- D ．{1,0,2}-2．（2024年全国甲卷高考真题）若集合{}1,2,3,4,5,9A =，{}1B x x A =+∈，则A B = （ ） A ．{}1,3,4 B ．{}2,3,4 C ．{}1,2,3,4 D ．{}0,1,2,3,4,93．（2023∙北京∙高考真题）已知集合{20},{10}M xx N x x =+≥=-<∣∣，则M N ⋂=（ ） A ．{21}x x -≤<∣ B ．{21}xx -<≤∣ C ．{2}xx ≥-∣ D ．{1}x x <∣ 4．（2023全国新Ⅰ卷高考真题）已知集合{}2,1,0,1,2M =--，{}260N x x x =--≥，则M N ⋂=（ ） A ．{}2,1,0,1-- B ．{}0,1,2 C ．{}2- D ．{}25．（2022∙全国新Ⅱ卷高考真题）已知集合{}{}1,1,2,4,11A B x x =-=-≤，则A B = （ ） A ．{1,2}- B ．{1,2} C ．{1,4} D ．{1,4}- 6．（2022年全国乙卷∙高考真题）集合{}{}2,4,6,8,10,16M N x x ==-<<，则M N ⋂=（ ） A ．{2,4} B ．{2,4,6} C ．{2,4,6,8} D ．{2,4,6,8,10}7．（2022年全国甲卷∙高考真题）设集合5{2,1,0,1,2},02A B x x ⎧⎫=--=≤<⎨⎬⎩⎭∣，则A B = （ ） A ．{}0,1,2 B ．{2,1,0}-- C ．{0,1} D ．{1,2}8．（2022全国新Ⅰ卷∙高考真题）若集合{4},{31}M x N x x =<=≥∣，则M N ⋂=（ ） A ．{}02x x ≤< B ．123x x ⎧⎫≤<⎨⎬⎩⎭ C ．{}316x x ≤< D ．1163x x ⎧⎫≤<⎨⎬⎩⎭9．（2021年全国乙卷∙高考真题）已知集合{}21,S s s n n ==+∈Z ，{}41,T t t n n ==+∈Z ，则S T?（ ）A ．∅B ．SC ．TD ．Z10．（2021年全国甲卷∙高考真题）设集合{}{}1,3,5,7,9,27M N x x ==>，则M N ⋂=（ ）A ．{}7,9B ．{}5,7,9C ．{}3,5,7,9D ．{}1,3,5,7,911．（2021年全国甲卷∙高考真题）设集合{}104,53M x x N x x ⎧⎫=<<=≤≤⎨⎬⎩⎭，则M N ⋂=（ ）A ．103x x ⎧⎫<≤⎨⎬⎩⎭ B ．143x x ⎧⎫≤<⎨⎬⎩⎭C ．{}45x x ≤<D ．{}05x x <≤12．（2021全国新Ⅰ卷∙高考真题）设集合{}24A x x =-<<，{}2,3,4,5B =，则A B = （ ）A ．{}2B ．{}2,3C ．{}3,4D ．{}2,3,4考点03 并集1．（2024∙北京∙高考真题）已知集合{|31}M x x =-<<，{|14}N x x =-≤<，则M N ⋃=（ ） A ．{}11x x -≤< B ．{}3x x >-C ．{}|34x x -<<D ．{}4x x <2．（2022∙浙江∙高考真题）设集合{1,2},{2,4,6}A B ==，则A B ⋃=（ ）A ．{2}B ．{1,2}C ．{2,4,6}D ．{1,2,4,6}3．（2021∙北京∙高考真题）已知集合{}|11A x x =-<<，{}|02B x x =≤≤，则A B ⋃=（ ）A ．{}|12x x -<<B ．{}|12x x -<≤C ．{}|01x x ≤<D ．{}|02x x ≤≤4．（2020∙山东∙高考真题）设集合A ={x |1≤x ≤3}，B ={x |2<x <4}，则A ∪B =（ ）A ．{x |2<x ≤3}B ．{x |2≤x ≤3}C ．{x |1≤x <4}D ．{x |1<x <4}考点04 补集1．（2024年全国甲卷∙高考真题）已知集合{}{}1,2,3,4,5,9,A B A ==，则()A A B ⋂=ð（ ） A ．{}1,4,9 B ．{}3,4,9 C ．{}1,2,3 D ．{}2,3,52．（2023年全国乙卷∙高考真题）设全集{}0,1,2,4,6,8U =，集合{}{}0,4,6,0,1,6M N ==，则U M N ⋃=ð（ ） A ．{}0,2,4,6,8 B ．{}0,1,4,6,8 C ．{}1,2,4,6,8 D ．U3．（2023年全国乙卷∙高考真题）设集合U =R ，集合{}1M x x =<，{}12N x x =-<<，则{}2x x ≥=（ ）A ．()U M N ðB ．U N M ðC ．()U M N ðD ．U M N ⋃ð4．（2022∙全国乙卷∙高考真题）设全集{1,2,3,4,5}U =，集合M 满足{1,3}U M =ð，则（ ）A ．2M ∈B ．3M ∈C ．4M ∉D ．5M ∉5．（2022∙北京∙高考真题）已知全集{33}U x x =-<<，集合{21}A x x =-<≤，则U A =ð（ ） A ．(2,1]- B ．(3,2)[1,3)-- C ．[2,1)- D ．(3,2](1,3)--6．（2021全国新Ⅱ卷∙高考真题）设集合{1,2,3,4,5,6},{1,3,6},{2,3,4}U A B ===，则()U A B = ð（ ）A ．{3}B ．{1,6}C ．{5,6}D ．{1,3}7．（2020全国新Ⅰ卷∙高考真题）已知全集{},,,U a b c d =，集合{},M a c =，则U M ð等于（ ） A ．∅ B ．{},a c C ．{},b d D ．{},,,a b c d考点05 充分条件与必要条件1．（2024∙全国甲卷∙高考真题）设向量()()1,,,2a x x b x =+= ，则（ ）A ．“3x =-”是“a b ⊥ ”的必要条件B ．“3x =-”是“//a b ”的必要条件C ．“0x =”是“a b ⊥ ”的充分条件D ．“1x =-”是“//a b ”的充分条件2．（2024∙天津∙高考真题）设,a b ∈R ，则“33a b =”是“33a b =”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件3．（2024∙北京∙高考真题）设 a ，b 是向量，则“()()ꞏ0a b a b +-= ”是“a b =- 或a b = ”的（ ）． A ．充分不必要条件 B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件4．（2023∙北京∙高考真题）若0xy ≠，则“0x y +=”是“2yxx y +=-”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件5．（2023∙全国甲卷∙高考真题）设甲：22sin sin 1αβ+=，乙：sin cos 0αβ+=，则（ ）A ．甲是乙的充分条件但不是必要条件B ．甲是乙的必要条件但不是充分条件C ．甲是乙的充要条件D ．甲既不是乙的充分条件也不是乙的必要条件6．（2023∙天津∙高考真题）已知,R a b ∈，“22a b =”是“222a b ab +=”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分又不必要条件7．（2023∙全国新Ⅰ卷∙高考真题）记n S 为数列{}n a 的前n 项和，设甲：{}n a 为等差数列；乙：{}n S n为等差数列，则（ ）A ．甲是乙的充分条件但不是必要条件B ．甲是乙的必要条件但不是充分条件C ．甲是乙的充要条件D ．甲既不是乙的充分条件也不是乙的必要条件8．（2022∙浙江∙高考真题）设x ∈R ，则“sin 1x =”是“cos 0x =”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件9．（2022∙北京∙高考真题）设{}n a 是公差不为0的无穷等差数列，则“{}n a 为递增数列”是“存在正整数0N ，当0n N >时，0n a >”的（ ）A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件10．（2021∙全国甲卷∙高考真题）等比数列{}n a 的公比为q ，前n 项和为n S ，设甲：0q >，乙：{}n S 是递增数列，则（ ）A ．甲是乙的充分条件但不是必要条件B ．甲是乙的必要条件但不是充分条件C ．甲是乙的充要条件D ．甲既不是乙的充分条件也不是乙的必要条件考点06 全称量词与存在量词1．（2024∙全国新Ⅱ卷∙高考真题）已知命题p ：x ∀∈R ，|1|1x +>；命题q ：0x ∃>，3x x =，则（ ） A ．p 和q 都是真命题B ．p ⌝和q 都是真命题C ．p 和q ⌝都是真命题D ．p ⌝和q ⌝都是真命题2．（2020∙全国新Ⅰ卷∙高考真题）下列命题为真命题的是（ ）A ．10>且34>B ．12>或45>C ．x R ∃∈，cos 1x >D ．x ∀∈R ，20x ≥参考答案考点01 集合间的基本关系1．（2023∙全国新Ⅱ卷∙高考真题）设集合{}0,A a =-，{}1,2,22B a a =--，若A B ⊆，则=a （ ）． A ．2 B ．1 C ．23 D ．1-【答案】B【详细分析】根据包含关系分20a -=和220a -=两种情况讨论，运算求解即可.【答案详解】因为A B ⊆，则有：若20a -=，解得2a =，此时{}0,2A =-，{}1,0,2B =，不符合题意；若220a -=，解得1a =，此时{}0,1A =-，{}1,1,0B =-，符合题意；综上所述：1a =.故选：B.2．（2020全国新Ⅰ卷∙高考真题）已知a ∈R ，若集合{}1,M a =，{}1,0,1N =-，则“0a =”是“M N ⊆”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件【答案】A【详细分析】根据充分条件和必要条件的定义即可求解.【答案详解】当0a =时，集合{}1,0M =，{}1,0,1N =-，可得M N ⊆，满足充分性，若M N ⊆，则0a =或1a =-，不满足必要性，所以“0a =”是“M N ⊆”的充分不必要条件，故选：A.考点02 交集1．（2024∙全国新Ⅰ卷高考真题）已知集合{}355,{3,1,0,2,3}A x x B =-<<=--∣，则A B = （ ） A ．{1,0}- B ．{2,3} C ．{3,1,0}-- D ．{1,0,2}-【答案】A【详细分析】化简集合A ，由交集的概念即可得解.【答案详解】因为{{}|,3,1,0,2,3A x x B =<<=--，且注意到12<<，从而A B = {}1,0-.故选：A.2．（2024年全国甲卷高考真题）若集合{}1,2,3,4,5,9A =，{}1B x x A =+∈，则A B = （ ）A ．{}1,3,4B ．{}2,3,4C ．{}1,2,3,4D ．{}0,1,2,3,4,9【答案】C 【详细分析】根据集合B 的定义先算出具体含有的元素，然后根据交集的定义计算.【答案详解】依题意得，对于集合B 中的元素x ，满足11,2,3,4,5,9x +=，则x 可能的取值为0,1,2,3,4,8，即{0,1,2,3,4,8}B =，于是{1,2,3,4}A B ⋂=.故选：C3．（2023∙北京∙高考真题）已知集合{20},{10}M xx N x x =+≥=-<∣∣，则M N ⋂=（ ） A ．{21}x x -≤<∣ B ．{21}xx -<≤∣ C ．{2}xx ≥-∣ D ．{1}x x <∣ 【答案】A【详细分析】先化简集合,M N ，然后根据交集的定义计算.【答案详解】由题意，{20}{|2}M xx x x =+≥=≥-∣，{10}{|1}N x x x x =-<=<∣， 根据交集的运算可知，{|21}M N x x =-≤< .故选：A4．（2023全国新Ⅰ卷高考真题）已知集合{}2,1,0,1,2M =--，{}260N x x x =--≥，则M N ⋂=（ ） A ．{}2,1,0,1--B ．{}0,1,2C ．{}2-D ．{}2【答案】C 【详细分析】方法一：由一元二次不等式的解法求出集合N ，即可根据交集的运算解出．方法二：将集合M 中的元素逐个代入不等式验证，即可解出． 【答案详解】方法一：因为{}(][)260,23,N x x x ∞∞=--≥=--⋃+，而{}2,1,0,1,2M =--， 所以M N ⋂={}2-．故选：C ．方法二：因为{}2,1,0,1,2M =--，将2,1,0,1,2--代入不等式260x x --≥，只有2-使不等式成立，所以M N ⋂={}2-．故选：C ．5．（2022∙全国新Ⅱ卷高考真题）已知集合{}{}1,1,2,4,11A B x x =-=-≤，则A B = （ ）A ．{1,2}-B ．{1,2}C ．{1,4}D ．{1,4}- 【答案】B【详细分析】方法一：求出集合B 后可求A B ⋂.【答案详解】[方法一]：直接法因为{}|02B x x =≤≤，故{}1,2A B = ，故选：B.[方法二]：【最优解】代入排除法=1x -代入集合{}11B x x =-≤，可得21≤，不满足，排除A 、D ；4x =代入集合{}11B x x =-≤，可得31≤，不满足，排除C.故选：B.【整体点评】方法一：直接解不等式，利用交集运算求出，是通性通法；方法二：根据选择题特征，利用特殊值代入验证，是该题的最优解．6．（2022年全国乙卷∙高考真题）集合{}{}2,4,6,8,10,16M N x x ==-<<，则M N ⋂=（ ） A ．{2,4} B ．{2,4,6} C ．{2,4,6,8} D ．{2,4,6,8,10}【答案】A【详细分析】根据集合的交集运算即可解出．【答案详解】因为{}2,4,6,8,10M =，{}|16N x x =-<<，所以{}2,4M N = ．故选：A.7．（2022年全国甲卷∙高考真题）设集合5{2,1,0,1,2},02A B x x ⎧⎫=--=≤<⎨⎬⎩⎭∣，则A B = （ ）A ．{}0,1,2B ．{2,1,0}--C ．{0,1}D ．{1,2}【答案】A【详细分析】根据集合的交集运算即可解出．【答案详解】因为{}2,1,0,1,2A =--，502B x x ⎧⎫=≤<⎨⎬⎩⎭∣，所以{}0,1,2A B = ．故选：A.8．（2022全国新Ⅰ卷∙高考真题）若集合{4},{31}M x N x x =<=≥∣，则M N ⋂=（ ）A ．{}02x x ≤<B ．123x x ⎧⎫≤<⎨⎬⎩⎭ C ．{}316x x ≤< D ．1163x x ⎧⎫≤<⎨⎬⎩⎭【答案】D【详细分析】求出集合,M N 后可求M N ⋂. 【答案详解】1{16},{}3M x x N x x =≤<=≥∣0∣，故1163M N x x ⎧⎫⋂=≤<⎨⎬⎩⎭，故选：D9．（2021年全国乙卷∙高考真题）已知集合{}21,S s s n n ==+∈Z ，{}41,T t t n n ==+∈Z ，则S T ?（ ）A ．∅B ．SC ．TD ．Z【答案】C【详细分析】详细分析可得T S ⊆，由此可得出结论.【答案详解】任取t T ∈，则()41221t n n =+=⋅+，其中Z n ∈，所以，t S ∈，故T S ⊆，因此，S T T = .故选：C.10．（2021年全国甲卷∙高考真题）设集合{}{}1,3,5,7,9,27M N x x ==>，则M N ⋂=（ ）A ．{}7,9B ．{}5,7,9C ．{}3,5,7,9D ．{}1,3,5,7,9【答案】B【详细分析】求出集合N 后可求M N ⋂. 【答案详解】7,2N ⎛⎫=+∞ ⎪⎝⎭，故{}5,7,9M N ⋂=， 故选：B.11．（2021年全国甲卷∙高考真题）设集合{}104,53M x x N x x ⎧⎫=<<=≤≤⎨⎬⎩⎭，则M N ⋂=（ ） A ．103x x ⎧⎫<≤⎨⎬⎩⎭ B ．143x x ⎧⎫≤<⎨⎬⎩⎭ C ．{}45x x ≤<D ．{}05x x <≤【答案】B【详细分析】根据交集定义运算即可 【答案详解】因为1{|04},{|5}3M x x N x x =<<=≤≤，所以1|43M N x x ⎧⎫⋂=≤<⎨⎬⎩⎭, 故选：B.【名师点评】本题考查集合的运算，属基础题，在高考中要求不高，掌握集合的交并补的基本概念即可求解.12．（2021全国新Ⅰ卷∙高考真题）设集合{}24A x x =-<<，{}2,3,4,5B =，则A B = （ ）A ．{}2B ．{}2,3C ．{}3,4D ．{}2,3,4 【答案】B【详细分析】利用交集的定义可求A B ⋂.【答案详解】由题设有{}2,3A B ⋂=，故选：B .考点03 并集1．（2024∙北京∙高考真题）已知集合{|31}M x x =-<<，{|14}N x x =-≤<，则M N ⋃=（ ） A ．{}11x x -≤< B ．{}3x x >-C ．{}|34x x -<<D ．{}4x x <【答案】C【详细分析】直接根据并集含义即可得到答案.【答案详解】由题意得{}|34M x x N ⋃=-<<.故选：C.2．（2022∙浙江∙高考真题）设集合{1,2},{2,4,6}A B ==，则A B ⋃=（ ）A ．{2}B ．{1,2}C ．{2,4,6}D ．{1,2,4,6}【答案】D【详细分析】利用并集的定义可得正确的选项.【答案详解】{}1,2,4,6A B = ，故选：D.3．（2021∙北京∙高考真题）已知集合{}|11A x x =-<<，{}|02B x x =≤≤，则A B ⋃=（ ） A ．{}|12x x -<< B ．{}|12x x -<≤C ．{}|01x x ≤<D ．{}|02x x ≤≤【答案】B【详细分析】结合题意利用并集的定义计算即可.【答案详解】由题意可得：{}|12A B x x =-<≤ .故选：B.4．（2020∙山东∙高考真题）设集合A ={x |1≤x ≤3}，B ={x |2<x <4}，则A ∪B =（ ） A ．{x |2<x ≤3} B ．{x |2≤x ≤3}C ．{x |1≤x <4}D ．{x |1<x <4}【答案】C【详细分析】根据集合并集概念求解.【答案详解】[1,3](2,4)[1,4)A B ==U U故选：C【名师点评】本题考查集合并集，考查基本详细分析求解能力，属基础题.考点04 补集1．（2024年全国甲卷∙高考真题）已知集合{}{}1,2,3,4,5,9,A B A ==，则()A A B ⋂=ð（ ）A ．{}1,4,9B ．{}3,4,9C ．{}1,2,3D ．{}2,3,5【答案】D【详细分析】由集合B 的定义求出B ，结合交集与补集运算即可求解.【答案详解】因为{}{}1,2,3,4,5,9,A B A ==，所以{}1,4,9,16,25,81B =， 则{}1,4,9A B = ，(){}2,3,5A A B = ð故选：D 2．（2023年全国乙卷∙高考真题）设全集{}0,1,2,4,6,8U =，集合{}{}0,4,6,0,1,6M N ==，则U M N ⋃=ð（ ） A ．{}0,2,4,6,8 B ．{}0,1,4,6,8 C ．{}1,2,4,6,8 D ．U【答案】A【详细分析】由题意可得U N ð的值，然后计算U M N ⋃ð即可.【答案详解】由题意可得{}2,4,8U N =ð，则{}0,2,4,6,8U M N = ð.故选：A.3．（2023年全国乙卷∙高考真题）设集合U =R ，集合{}1M x x =<，{}12N x x =-<<，则{}2x x ≥=（ ） A ．()U M N ð B ．U N M ðC ．()U M N ðD ．U M N ⋃ð【答案】A【详细分析】由题意逐一考查所给的选项运算结果是否为{}|2x x ≥即可.【答案详解】由题意可得{}|2M N x x =< ，则(){}|2U M N x x =≥ ð，选项A 正确； {}|1U M x x =≥ð，则{}|1U N M x x =>- ð，选项B 错误；{}|11M N x x =-<< ，则(){|1U M N x x ⋂=≤-ð或}1x ≥，选项C 错误；{|1U N x x =≤-ð或}2x ≥，则U M N = ð{|1x x <或}2x ≥，选项D 错误；故选：A.4．（2022∙全国乙卷∙高考真题）设全集{1,2,3,4,5}U =，集合M 满足{1,3}U M =ð，则（ ） A ．2M ∈ B ．3M ∈ C ．4M ∉ D ．5M ∉【答案】A【详细分析】先写出集合M ,然后逐项验证即可【答案详解】由题知{2,4,5}M =,对比选项知，A 正确,BCD 错误故选:A5．（2022∙北京∙高考真题）已知全集{33}U x x =-<<，集合{21}A x x =-<≤，则U A =ð（ ） A ．(2,1]- B ．(3,2)[1,3)-- C ．[2,1)- D ．(3,2](1,3)--【答案】D【详细分析】利用补集的定义可得正确的选项．【答案详解】由补集定义可知：{|32U A x x =-<≤-ð或13}x <<，即(3,2](1,3)U A =-- ð，故选：D ．6．（2021全国新Ⅱ卷∙高考真题）设集合{1,2,3,4,5,6},{1,3,6},{2,3,4}U A B ===，则()U A B = ð（ ） A ．{3} B ．{1,6}C ．{5,6}D ．{1,3}【答案】B【详细分析】根据交集、补集的定义可求()U A B ⋂ð.【答案详解】由题设可得{}U 1,5,6B =ð，故(){}U 1,6A B ⋂=ð， 故选：B.7．（2020全国新Ⅰ卷∙高考真题）已知全集{},,,U a b c d =，集合{},M a c =，则U M ð等于（ ） A ．∅ B ．{},a cC ．{},b dD ．{},,,a b c d【答案】C【详细分析】利用补集概念求解即可. 【答案详解】{},U M b d =ð. 故选：C考点05 充分条件与必要条件1．（2024∙全国甲卷∙高考真题）设向量()()1,,,2a x x b x =+= ，则（ ）A ．“3x =-”是“a b ⊥”的必要条件B ．“3x =-”是“//a b ”的必要条件C ．“0x =”是“a b ⊥”的充分条件 D ．“1x =-”是“//a b ”的充分条件 【答案】C【详细分析】根据向量垂直和平行的坐标表示即可得到方程，解出即可.【答案详解】对A ，当a b ⊥ 时，则0a b ⋅=，所以(1)20x x x ⋅++=，解得0x =或3-，即必要性不成立，故A 错误；对C ，当0x =时，()()1,0,0,2a b == ，故0a b ⋅=，所以a b ⊥，即充分性成立，故C 正确；对B ，当//a b时，则22(1)x x +=，解得1x =±B 错误；对D ，当1x =-时，不满足22(1)x x +=，所以//a b不成立，即充分性不立，故D 错误. 故选：C.2．（2024∙天津∙高考真题）设,a b ∈R ，则“33a b =”是“33a b =”的（ ） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件 D ．既不充分也不必要条件【答案】C【详细分析】说明二者与同一个命题等价，再得到二者等价，即是充分必要条件.【答案详解】根据立方的性质和指数函数的性质，33a b =和33a b =都当且仅当a b =，所以二者互为充要条件. 故选：C.3．（2024∙北京∙高考真题）设 a ，b 是向量，则“()()ꞏ0a b a b +-=”是“a b =- 或a b = ”的（ ）． A ．充分不必要条件 B ．必要不充分条件 C ．充要条件 D ．既不充分也不必要条件【答案】B【详细分析】根据向量数量积详细分析可知()()0a b a b +⋅-= 等价于a b =，结合充分、必要条件详细分析判断.【答案详解】因为()()220a b a b a b +⋅-=-= ，可得22a b = ，即a b = ，可知()()0a b a b +⋅-= 等价于a b = ， 若a b = 或a b =- ，可得a b = ，即()()0a b a b +⋅-=，可知必要性成立；若()()0a b a b +⋅-= ，即a b =，无法得出a b = 或a b =- ， 例如()()1,0,0,1a b ==，满足a b = ，但a b ≠ 且a b ≠- ，可知充分性不成立；综上所述，“()()0a b a b +⋅-=”是“a b ≠ 且a b ≠- ”的必要不充分条件.故选：B.4．（2023∙北京∙高考真题）若0xy ≠，则“0x y +=”是“2y xx y+=-”的（ ） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件 D ．既不充分也不必要条件【答案】C【详细分析】解法一：由2xyy x +=-化简得到0x y +=即可判断；解法二：证明充分性可由0x y +=得到x y =-，代入x y y x+化简即可，证明必要性可由2x yy x +=-去分母，再用完全平方公式即可；解法三：证明充分性可由x y y x +通分后用配凑法得到完全平方公式，再把0x y +=代入即可，证明必要性可由x yy x+通分后用配凑法得到完全平方公式，再把0x y +=代入，解方程即可. 【答案详解】解法一： 因为0xy ≠，且2x yy x +=-，所以222x y xy +=-，即2220x y xy ++=，即()20x y +=，所以0x y +=.所以“0x y +=”是“2x yy x +=-”的充要条件. 解法二：充分性：因为0xy ≠，且0x y +=，所以x y =-， 所以112x y y yy x y y -+=+=--=--， 所以充分性成立；必要性：因为0xy ≠，且2x yy x +=-，所以222x y xy +=-，即2220x y xy ++=，即()20x y +=，所以0x y +=. 所以必要性成立.所以“0x y +=”是“2x yy x +=-”的充要条件. 解法三：充分性：因为0xy ≠，且0x y +=，所以()2222222222x y xy x y x y x y xy xy xyy x xy xy xy xy+-+++--+=====-， 所以充分性成立；必要性：因为0xy ≠，且2x yy x +=-，所以()()22222222222x y xy x y x y x y x y xy xy y x xy xy xy xy+-++++-+====-=-， 所以()20x y xy+=，所以()20x y +=，所以0x y +=，所以必要性成立.所以“0x y +=”是“2xyy x +=-”的充要条件. 故选：C5．（2023∙全国甲卷∙高考真题）设甲：22sin sin 1αβ+=，乙：sin cos 0αβ+=，则（ ） A ．甲是乙的充分条件但不是必要条件 B ．甲是乙的必要条件但不是充分条件C ．甲是乙的充要条件D ．甲既不是乙的充分条件也不是乙的必要条件【答案】B【详细分析】根据充分条件、必要条件的概念及同角三角函数的基本关系得解. 【答案详解】当22sin sin 1αβ+=时，例如π,02αβ==但sin cos 0αβ+≠， 即22sin sin 1αβ+=推不出sin cos 0αβ+=；当sin cos 0αβ+=时，2222sin sin (cos )sin 1αβββ+=-+=，即sin cos 0αβ+=能推出22sin sin 1αβ+=. 综上可知，甲是乙的必要不充分条件. 故选：B6．（2023∙天津∙高考真题）已知,R a b ∈，“22a b =”是“222a b ab +=”的（ ） A ．充分不必要条件 B ．必要不充分条件 C ．充分必要条件 D ．既不充分又不必要条件【答案】B【详细分析】根据充分、必要性定义判断条件的推出关系，即可得答案.【答案详解】由22a b =，则a b =±，当0a b =-≠时222a b ab +=不成立，充分性不成立； 由222a b ab +=，则2()0a b -=，即a b =，显然22a b =成立，必要性成立； 所以22a b =是222a b ab +=的必要不充分条件. 故选：B7．（2023∙全国新Ⅰ卷∙高考真题）记n S 为数列{}n a 的前n 项和，设甲：{}n a 为等差数列；乙：{}nS n为等差数列，则（ ）A ．甲是乙的充分条件但不是必要条件B ．甲是乙的必要条件但不是充分条件C ．甲是乙的充要条件D ．甲既不是乙的充分条件也不是乙的必要条件 【答案】C【详细分析】利用充分条件、必要条件的定义及等差数列的定义，再结合数列前n 项和与第n 项的关系推理判断作答.，【答案详解】方法1，甲：{}n a 为等差数列，设其首项为1a ，公差为d ， 则1111(1)1,,222212n n n n S S S n n n d d dS na d a d n a n n n +--=+=+=+--=+， 因此{}nS n为等差数列，则甲是乙的充分条件； 反之，乙：{}nS n为等差数列，即111(1)1(1)(1)n n n n n n S S nS n S na S n n n n n n +++-+--==+++为常数，设为t ，即1(1)n nna S t n n +-=+，则1(1)n n S na t n n +=-⋅+，有1(1)(1),2n n S n a t n n n -=--⋅-≥，两式相减得：1(1)2n n n a na n a tn +=---，即12n n a a t +-=，对1n =也成立， 因此{}n a 为等差数列，则甲是乙的必要条件， 所以甲是乙的充要条件，C 正确.方法2，甲：{}n a 为等差数列，设数列{}n a 的首项1a ，公差为d ，即1(1)2n n n S na d -=+， 则11(1)222n S n d d a d n a n-=+=+-，因此{}n S n 为等差数列，即甲是乙的充分条件；反之，乙：{}nS n 为等差数列，即11,(1)1n n n S S S D S n D n n n+-==+-+， 即1(1)n S nS n n D =+-，11(1)(1)(2)n S n S n n D -=-+--，当2n ≥时，上两式相减得：112(1)n n S S S n D --=+-，当1n =时，上式成立， 于是12(1)n a a n D =+-，又111[22(1)]2n n a a a nD a n D D +-=+-+-=为常数， 因此{}n a 为等差数列，则甲是乙的必要条件， 所以甲是乙的充要条件. 故选：C8．（2022∙浙江∙高考真题）设x ∈R ，则“sin 1x =”是“cos 0x =”的（ ） A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件 【答案】A【详细分析】由三角函数的性质结合充分条件、必要条件的定义即可得解. 【答案详解】因为22sin cos 1x x +=可得： 当sin 1x =时，cos 0x =，充分性成立； 当cos 0x =时，sin 1x =±，必要性不成立； 所以当x ∈R ，sin 1x =是cos 0x =的充分不必要条件. 故选：A.9．（2022∙北京∙高考真题）设{}n a 是公差不为0的无穷等差数列，则“{}n a 为递增数列”是“存在正整数0N ，当0n N >时，0n a >”的（ ） A ．充分而不必要条件 B ．必要而不充分条件 C ．充分必要条件 D ．既不充分也不必要条件【答案】C【详细分析】设等差数列{}n a 的公差为d ，则0d ≠，利用等差数列的通项公式结合充分条件、必要条件的定义判断可得出结论.【答案详解】设等差数列{}n a 的公差为d ，则0d ≠，记[]x 为不超过x 的最大整数. 若{}n a 为单调递增数列，则0d >，若10a ≥，则当2n ≥时，10n a a >≥；若10a <，则()11n a a n d +-=， 由()110n a a n d =+->可得11a n d >-，取1011a N d ⎡⎤=-+⎢⎥⎣⎦，则当0n N >时，0n a >，所以，“{}n a 是递增数列”⇒“存在正整数0N ，当0n N >时，0n a >”； 若存在正整数0N ，当0n N >时，0n a >，取N k *∈且0k N >，0k a >， 假设0d <，令()0n k a a n k d =+-<可得k a n k d >-，且k ak k d->， 当1k a n k d ⎡⎤>-+⎢⎥⎣⎦时，0n a <，与题设矛盾，假设不成立，则0d >，即数列{}n a 是递增数列.所以，“{}n a 是递增数列”⇐“存在正整数0N ，当0n N >时，0n a >”.所以，“{}n a 是递增数列”是“存在正整数0N ，当0n N >时，0n a >”的充分必要条件. 故选：C.10．（2021∙全国甲卷∙高考真题）等比数列{}n a 的公比为q ，前n 项和为n S ，设甲：0q >，乙：{}n S 是递增数列，则（ ）A ．甲是乙的充分条件但不是必要条件B ．甲是乙的必要条件但不是充分条件C ．甲是乙的充要条件D ．甲既不是乙的充分条件也不是乙的必要条件 【答案】B【详细分析】当0q >时，通过举反例说明甲不是乙的充分条件；当{}n S 是递增数列时，必有0n a >成立即可说明0q >成立，则甲是乙的必要条件，即可选出答案． 【答案详解】由题，当数列为2,4,8,--- 时，满足0q >， 但是{}n S 不是递增数列，所以甲不是乙的充分条件．若{}n S 是递增数列，则必有0n a >成立，若0q >不成立，则会出现一正一负的情况，是矛盾的，则0q >成立，所以甲是乙的必要条件． 故选：B ．【名师点评】在不成立的情况下，我们可以通过举反例说明，但是在成立的情况下，我们必须要给予其证明过程．考点06 全称量词与存在量词1．（2024∙全国新Ⅱ卷∙高考真题）已知命题p ：x ∀∈R ，|1|1x +>；命题q ：0x ∃>，3x x =，则（ ） A ．p 和q 都是真命题 B ．p ⌝和q 都是真命题 C ．p 和q ⌝都是真命题 D ．p ⌝和q ⌝都是真命题【答案】B【详细分析】对于两个命题而言，可分别取=1x -、1x =，再结合命题及其否定的真假性相反即可得解. 【答案详解】对于p 而言，取=1x -，则有101x +=<，故p 是假命题，p ⌝是真命题，对于q 而言，取1x =，则有3311x x ===，故q 是真命题，q ⌝是假命题， 综上，p ⌝和q 都是真命题. 故选：B.2．（2020∙全国新Ⅰ卷∙高考真题）下列命题为真命题的是（ ） A ．10>且34> B ．12>或45> C ．x R ∃∈，cos 1x > D ．x ∀∈R ，20x ≥【答案】D【详细分析】本题可通过43>、12<、45<、cos 1≤x 、20x ≥得出结果. 【答案详解】A 项：因为43>，所以10>且34>是假命题，A 错误； B 项：根据12<、45<易知B 错误； C 项：由余弦函数性质易知cos 1≤x ，C 错误； D 项：2x 恒大于等于0，D 正确， 故选：D.。

《集合高考试题汇编》1.已知{(,)|20},{(,)|0}A x y ax y B x y x y b =++>=-+<,M 点的坐标为(1,1),若 ,M A M B ∈∉且,,a b 则应满足A.30a b >->且B.30a b >-<且C.30a b >-≤且D.30a b >-≥且 【参考答案】D.2.已知集合,{|21},{|x U R M x N y y ==>==则A.MN N = B.M N N = C.()U M N R =ð D.(){0}U M N =ð【参考答案】D.3.设全集U 是实数集R ,={|20},M x x -≥{|3},N x x =<则()U M N =ðA.{|23}x x ≤<B.{|2}x x <C.{|2}x x ≤D.{|3}x x ≥ 【参考答案】B.4.设集合{|11},{|02}A x x B x x =-<<=<<,则A B =A.(0,1)B.(1,2)-C.(1,2)D.(1,0)- 【参考答案】B.5.已知集合{1,2,3},{2,3,4},M N ==则A.M N ⊆B.N M ⊆C.{2,3}M N =D.{1,4}M N = 【参考答案】C.6.设集合2{1,0,1},{|},M N x x x =-=≤则M N =A.{0}B.{0,1}C.{1,1}-D.{1,0,1}- 【参考答案】B.7.已知集合{|123},{|24},A x x x B x x =<-≤<=-≤<或则_________.A B = 【参考答案】(,4)-∞8.若集合{|2},{|}A x x B x x a =≤=≥满足{2},A B =则实数_____.a = 【参考答案】29.已知集合{|1},{|},A x x B x x a =≤=≥且,A B R =则实数a 的取值范围是_________. 【参考答案】(,2]-∞ 10.若集合{|1},{|02},A x x B x x =>=<<则_______.A B = 【参考答案】(1,2)11.已知集合1{|2},{|0},1A x xB x x =<=>+则_______.A B =【参考答案】(1,2)-12.若全集,U R =集合{|1}{|0},A x x x x =≥≤则_____.U A =ð 【参考答案】(0,1)13.若集合2{|1},{|4},A x x B x x =≥=≤则_______.A B = 【参考答案】[1,2]14.若集合{|210},{|12},A x x B x x =+>=-<则_______.A B =【参考答案】1(,3)2- 15.若集合{1,2,},{2,5}.A k B ==若{1,2,3,5}A B =,则____.k = 【参考答案】316.已知集合3{|0},{|3},1x M x N x x x +=<=≤--则集合{|1}x x ≥= A.M N B.M N C.()R C M N D.()R C M N 【参考答案】D.17.已知集合{|35},{|55},M x x N x x =-<≤=-<<则M N = A.{|55}x x -<< B.{|35}x x -<< C.{|55}x x -<≤ D.{|35}x x -<≤ 【参考答案】B.18.已知,A B 均为集合{1,3,5,7,9}U =的子集,且{3},(){9},U A B B A ==ð则A = A.{1,3} B.{3,7,9} C.{3,5,9} D.{3,9} 【参考答案】D.19.已知,M N 为集合I 的非空真子集,且,M N 不相等,若,I N M =∅ð则M N = A.M B.N C.I D.∅ 【参考答案】A.20.已知全集{0,1,2,3,4,5,6,7,8,9}U =,集合{0,1,3,5,8}A =,集合{2,4,5,6,8}B =,则 ()()U U A B =痧 A.{5,8} B.{7,9} C.{0,1,3} D.{2,4,6} 【参考答案】B.21.已知集合4{|0log 1},{|2},A x x B x x =<<=≤则A B =A.(0,1)B.(0,2]C.(1,2)D.(1,2] 【参考答案】D.22.已知全集,U R ={|0},{|1},A x x B x x =≤=≥则()U AB =ð A.{|0}x x ≥ B.{|1}x x ≤ C.{|01}x x ≤≤ D.{|01}x x << 【参考答案】D.23.设集合{|23},{|8},,S x x T x a x a S T R =->=<<+=则a 的取值范围是A.(3,1)--B.[3,1]--C.(,3][1,)-∞--+∞D.(,3)(1,-∞--+∞ 【参考答案】A.24.设集合{|1},{|2},A x R x a T x R x b =∈-<=∈->若,A B ⊆则实数,a b 必满足A.3a b +≤B.3a b +≥C.3a b -≤D.3a b -≥ 【参考答案】D.25.已知集合1{|349},{|46,(0,)},A x R x x B x R x t t t=∈++-≤=∈=+-∈+∞则集合_______.A B = 【参考答案】[2,5]-26.已知集合{|23},{|()(2)0},A x R x B x R x m x =∈+<=∈--<且(1,),A B n =- 则____,_____.m n == 【参考答案】1,1m n =-=27..已知集合{|2},{|1},A x R x B x R x =∈≤=∈≤则AB =A.(,2]-∞B.[1,2]C.[2,2]-D.[2,1]- 【参考答案】D.28.已知全集,U R =集合2{|20},A x x x =->则U A =ðA.[0,2]B.(0,2)C.(,0)(2,)-∞+∞D.(,0][2,)-∞+∞ 【参考答案】A.29.若集合{,,,}{1,2,3,4},a b c d =且下列四个关系：①1;a =②1;b ≠③2;c =④4d ≠有且仅有一个是正确的,则符合条件的有序数组(,,,)a b c d 的个数是_____________. 【参考答案】630.满足1234{,,,},M a a a a ⊆且12312{,,}{,}Ma a a a a =的集合M 的个数是A.1B.2C.3D.4 【参考答案】B.31.集合2{0,2,},{1,},A a B a ==若{0,1,2,4,16},A B =则a 的值为 A.0 B.1 C.2 D.4 【参考答案】D.32.已知全集,U R =集合{|12},M x x =-<则U M =ðA.{|13}x x -<<B.{|13}x x -≤≤C.{|13}x x x <->或D.{|13}x x x ≤-≥或 【参考答案】D.33.设集合2{|60},M x x x =+-<{|13},N x x =≤≤则M N =A.[1,2)B.[1,2]C.(2,3]D.[2,3] 【参考答案】A.34.已知全集{0,1,2,3,4}U =,集合{1,2,3}A =,集合{2,4}B =,则()U A B =ð A.{1,2,4} B.{2,3,4} C.{0,2,4} D.{0,2,3,4 35.已知集合{0,1,2}A =,集合{|,}B x y x A y A =-∈∈中元素的个数是 A.1 B.3 C.5 D.9 【参考答案】C.36.设集合{|12},A x x =-<集合{|2,[0,2]}xB y y x ==∈,则A B = A.[0,2] B.(1,3) C.[1,3) D.(1,4) 【参考答案】C.37.设集合2{|(1)37,},A x x x x R =-<+∈则集合A Z 中有______个元素. 【参考答案】638.已知集合2{|log 2},A x x =≤(,)B a =-∞,若,A B ⊆则实数a 的取值范围是(,)c +∞,其中_____.c = 【参考答案】439.设集合{1,1,3},A =-2{2,4},{3},B a a A B =++=则实数a 的值为________. 【参考答案】140.已知集合{1,1,2,4},A =-{1,0,2},B =-则_____.A B = 【参考答案】{1,2}-41.设集合222{(,)|(2),,},2m A x y x y m x y R =≤-+≤∈{(,)|2B x y m x y =≤+≤21,m +,}x y R ∈.若,A B ≠∅则实数m 的取值范围是__________.【参考答案】1[,2242.已知集合{1,2,4},A ={2,4,6},B =则_____.A B = 【参考答案】{1,2,4,6}43.已知集合{2,1,3,4},A =--{1,2,3},B =-则_____.A B = 【参考答案】{1,3}-44.定义集合运算：{|,,}.A B z z xy x A y B *==∈∈设{1,2},{0,2},A B ==则集合A B *的所有元素之和为A.0B.2C.3D.6 【参考答案】C.45.已知全集U A B =中有m 个元素,()()U U A B 痧中有n 个元素.若A B 非空,则A B 的元素个数为A.mnB.m n +C.n m -D.m n - 【参考答案】D.46.若集合{|1,},A x x x R =≤∈2{|,},B y y x x R ==∈则A B =A.{|11}x x -≤≤B.{|0}x x ≥C.{|01}x x ≤≤D.∅ 【参考答案】C.47.若集合{|1213},A x x =-≤+≤2{|0},x B x x-=≤则A B =A.{|10}x x -≤<B.{|01}x x <≤C.{|02}x x ≤≤D.{|01}x x ≤≤ 【参考答案】B.48.若集合{1,1},A =-{0,2},B =则集合{|,,}z z x y x A y B =+∈∈中的元素个数为 A.5 B.4 C.3 D.2 【参考答案】C.49.已知全集{1,2,3,4,5}U =,集合2{|320},A x x x =-+={|2,},B x x a a A ==∈则集合 ()U A B ð中元素的个数为A.1B.2C.3D.4 【参考答案】B.50.若不等式20x x -≤的解集为M ,函数()ln(1)f x x =-的定义域为N ,则M N = A.[0,1) B.(0,1) C.[0,1] D.(1,0]- 【参考答案】A.51.集合{|12},A x x =-≤≤{|1},B x x =<则()R A B =ðA.{|1}x x >B.{|1}x x ≥C.{|12}x x <≤D.{|12}x x ≤≤ 【参考答案】D.52.设集合22{|cos sin ,},M y y x x x R ==-∈1{|N x x i=-<,i x 为虚数单位},R ∈则M N =A.(0,1)B.(0,1]C.[0,1)D.[0,1] 【参考答案】C.53.集合{|lg 0},M x x =>集合2{|4},N x x =≤则M N =A.(1,2)B.[1,2)C.(1,2]D.[1,2] 【参考答案】C.54.设全集为,R 函数()f x =M ,则R M =ðA.[1,1]-B.(1,1)-C.(,1][1,-∞-+∞D.(,1)(1,)-∞-+∞【参考答案】D.55.设集合{|0,},M x x x R =≥∈2{|1,},N x x x R =<∈则M N =A.[0,1]B.[0,1)C.(0,1]D.(0,1) 【参考答案】B.56.已知集合{|23},A x x =-≤≤{|14},B x x x =<->或那么集合()R A B =ðA.{|24}x x -≤<B.{|34}x x x ≤≥或 C.{|21}x x -≤<- D.{|13}x x -≤≤ 【参考答案】D.57.集合2{|03},{|9}P x Z x M x R x =∈≤<=∈≤,则PM =A.{1,2}B.{0,1,2}C.{|03}x x ≤<D.{|03}x x ≤≤ 【参考答案】B.58.已知集合2{|1},{}.P x x M a =≤=若,P M P =则a 的取值范围是A.(,1]-∞-B.[1,)+∞C.[1,1]-D.(,1][1,)-∞-+∞ 【参考答案】C.59.已知集合{|320},{|(1)(3)0}.A x R x B x R x x =∈+>=∈+->则A B =A.(,1)-∞-B.2(1,)3--C.2(,2)3- D.(3,)+∞【参考答案】D.60.已知集合{1,0,1},{|11},A B x x =-=-≤<则A B =A.{0}B.{1,0}-C.{0,1}D.{1,0,1}- 【参考答案】B.61.已知集合2{|20},{0,1,2},A x x x B =-==则A B =A.{0}B.{0,1}C.{0,2}D.{0,1,2} 【参考答案】C.62.已知{|(1,0)(0,1),},{|(1,1)(1,1),P m m R Q n n R ==+∈==+-∈a a b b 是两个向量集合,则P Q =A.{(1,1)}B.{(1,1)}-C.{(1,0)}D.{(0,1)} 【参考答案】A.63.集合22{(,)|1},{(,)|3},416x x y A x y B x y y =+===则A B 的子集的个数是 A.4 B.3 C.2 D.1 【参考答案】A.64.已知21{|log ,1},{|,2},U y y x x P y y x x==>==>则U P =ðA.1[,)2+∞B.1(0,)2C.(0,)+∞D.1(,0][,)2-∞+∞ 【参考答案】A.65.已知集合21{|()1},{|680},2x A x B x x x =≤=-+≤则()R A B =ðA.{|0}x x ≤B.{|24}x x ≤≤C.{|024}x x x ≤<>或D.{|024}x x x <≤≥或 【参考答案】C.66.设U 为全集,,A B 是集合,则“存在集合C 使得,U A C B C ⊆⊆ð”是“A B =∅”的 A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分也不必要条件 【参考答案】C.67．已知集合{|212}M x x =-≤-≤和{|21,1,2,}N x x k k ==-=⋅⋅⋅的关系的韦恩图如图所示,则阴影部分所示的集合的元素共有A.3个B.2个C.1个D.无穷多个 【参考答案】A.68.若集合{|21},A x x =-<<{|02},B x x =<<则集合AB =A.{|11}x x -<<B.{|21}x x -<<C.{|22}x x -<< D.{|01}x x << 【参考答案】D.69.集合22{(,)|,1},{(,)|,},A x y x y x y B x y x y y x =+===为实数且为实数且则A B的元素个数是A.4B.3C.2D.1 【参考答案】C. 70.设集合={12,3,4,5,6},{1,2,4},U M =，则U M =ðA.UB.{1,3,5}C.{3,5,6}D.{2,4,6} 【参考答案】C. 71.设集合={12,3},{4,5},{|,,}A B M x x a b a A b B ===+∈∈，,则M 中元素的个数为 A.3 B.4 C.5 D.6 【参考答案】B.72.设集合22={|20,},{|20,},M x x x x R N x x x x R +=∈=-=∈则M N = A.{0} B.{0,2} C.{2,0}- D.{2,0,2}- 【参考答案】D.73.已知集合={1,0,1},{0,1,2},M N -=则M N =A.{0,1}B.{1,0,2}-C.{1,0,1,2}-D.{1,0,1}- 【参考答案】C.74.已知集合={|lg ,1},{2,1,1,2},A y R y x x B ∈=>=--则下列结论中正确的是A.{2,1}A B =--B.()(,0)R A B =-∞ð C.(0,)A B =+∞ D.(){2,1}R A B =--ð 【参考答案】D.75.若集合21={|213},{|0},3x A x x B x x+-<=<-则A B =A.1{|123}2x x x -<<-<<或 B. {|23}x x <<C. 1{|2}2x x -<<D.1{|1}2x x -<<-【参考答案】D.76.若集合121={|log },2A x x ≥则R A =ðA.2(,0](,)2-∞+∞ B.,)2+∞ C.2(,0][,)2-∞+∞ D.,)2+∞ 【参考答案】A.77.已知集合={1,2,3,4,5,6},{4,5,6,7,8},A B =则满足S A S B ⊆≠∅且的集合S 的个数是A.57B.56C.49D.8 【参考答案】B.78.设集合={|32},{|13},M m Z m N n Z n ∈-<<=∈-≤≤则M N =A.{0,1}B.{1,0,1}-C.{0,1,2}D.{1,0,1,2}- 【参考答案】B.79.已知集合={1,3,5,7,9},{0,3,6,9,12},A B =则N A B =ðA.{1,5,7}B.{3,5,7}C.{1,3,9}D.{1,2,3}【参考答案】A.80.集合={4,5,7,9},{3,4,7,8,9},A B =全集U AB =,则集合()U A B ð中的元素共有A.3个B.4个C.5个D.6个 【参考答案】A.81.设集合{|3},A x x =>1{|0},4x B x x -=<-则A B =A.∅B.(3,4)C.(2,1)-D.(4,)+∞ 【参考答案】B.82.已知集合{|2,},A x x x R =≤∈{4,},B x x Z =∈则A B = A.(0,2) B.[0,2] C.{0,2} D.{0,1,2} 【参考答案】D.83.若集合{1,2,3,4,5},A ={(,)|,,},B x y x A y A x y A =∈∈-∈则集合B 中所含元素的个数为A.3B.6C.8D.10 【参考答案】D.84.已知集合{A ={1,},,B m A B A ==则m =A.0B.03或C.1D.13或 【参考答案】B.85.已知集合2{|20},{|A x x x B x x =->=<<则A.A B =∅B.A B R =C.B A ⊆D.A B ⊆ 【参考答案】B.86.已知集合2{|(1)4,}M x x x R =-<∈,{1,0,1,2,3}N =-,则M N =A.{0,1,2}B.{1,0,1,2- C.{1,0,2,3}- D.{0,1,2,3} 【参考答案】A.87.已知集合2{|230},{|22},A x x x B x x =--≥=-≤<则A B =A.[2,1]--B.[1,2)-C.[1,1]-D.[1,2) 【参考答案】A.88.设集合{0,1,2}M =,2{|320},N x x x =-+≤则M N =A.{1}B.{2}C.{0,1}D.{1,2} 【参考答案】D.89.设集合2{|340},M x x x =--<{|05},N x x =≤≤则M N =A.(0,4]B.[0,4)C.[1,0)-D.(1,0]- 【参考答案】B.90.设集合{1,2,3,4,5},{2,4},{3,4,5},{3,4},U A B C ====则()()___.U A B C =ð 【参考答案】{2,5}91.若{|3},{|21},xA x R xB x R =∈<=∈>则A B =_______. 【参考答案】(0,3)92.设2{0,1,2,3},{|0},U A x U x mx ==∈+=若{1,2},U A =ð则实数_____.m = 【参考答案】3-93.已知全集{1,2,3,4},U =集合{1,2},{2,3},A B ==则()U AB =ð A.{1,3,4} B.{3,4}C.{3}D.{4} 【参考答案】D.94.设全集{|110},{1,2,3,5,8},{1,3,5,7,9}U n N n A B =∈≤≤==,则()__.U A B =ð【参考答案】{7,9}95.已知,{|0},{|1},U R A x x B x x ==>=≤-则()()U UAB B A =痧A.∅B.{|0}x x ≤C.{|1}x x >-D.{|01}x x x >≤-或 【参考答案】D.96.设,{|0},{|1},U R A x x B x x ==>=>则U A B =ðA.{|01}x x ≤<B.{|01}x x <≤C.{|0}x x <D.{|1}x x > 【参考答案】B.97.设2{|4},{|4},P x x Q x x =<=<则A.P Q ⊆B.Q P ⊆C.R P Q ⊆ðD.R Q P ⊆ð 【参考答案】B.98.设集合2{|14},{|230},A x x B x x x =<<=--≤则R A B =ðA.(1,4)B.(3,4)C.(1,3)D.(1,2)(3,4) 【参考答案】B.99.设集合2{|2},{|340},S x x T x x x =>-=+-≤则()R S T = ?A.(2,1]-B.(,4]-∞-C.(,1]-∞D.[1,)+∞ 【参考答案】C.100.设全集{|2},U x N x =∈≥集合2{|5},A x N x =∈≥则U A =ð A.∅ B.{2} C.{5} D.{2,5} 【参考答案】B.101.设整数4,n ≥集合{1,2,3,,}.X n =⋅⋅⋅令集合{(,,)|,,,S x y z x y z X =∈且三条件xy <,z <,y z x <<}z x y <<恰好一个成立.若()x,y,z 和(,,)z w x 都在S 中,则下列选项中正确的是A.(),(,,)y,z,w S x y w S ∈∉B.(),(,,)y,z,w S x y w S ∈∈C.(),(,,)y,z,w S x y w S ∉∈D.(),(,,)y,z,w S x y w S ∉∉ 【参考答案】B.102.设S 是整数集Z 的非空子集,如果,,a b S ∀∈有,ab S ∈则称S 关于数的乘法是封闭的.若,T V 是Z 的两个不相交的非空子集,,T V Z =且,,,a b c T ∀∈有;abc T ∈,,,x y z V ∀∈ ,xyz T ∈则下列结论恒成立的是A.,T V 中至少有一个关于乘法是封闭的B.,T V 中至多有一个关于乘法是封闭的C.,T V 中有且只有一个关于乘法是封闭的D.,T V 中每一个关于乘法都是封闭的 【参考答案】A.103.已知{2,3,4,5,6,7},{3,4,5,7},{2,4,5,6}U M N ===,则 A.{4,6}M N = B.M N U = C.()U N M U =ð D.()U M N N =ð 【参考答案】B.104.某班共30人,其中15人喜爱篮球运动,10人喜爱乒乓球运动,8人对这两项运动都不喜爱,则喜爱篮球运动但不喜爱乒乓球运动的人数为__________. 【参考答案】12.105.已知集合{1,2,3},{2,,4},{2,3},A B m A B ===则____.m = 【参考答案】3106.设全集{1,2,3,4,5},{2,4},U U MN M N ===ð则N =A.{1,2,3}B.{1,3,5}C.{1,4,5}D.{2,3,4} 【参考答案】B.107.设集合2{1,0,1},{}},M N x x x =-==则M N =A.{1,0,1}-B.{0,1}C.{1}D.{0} 【参考答案】B.108.已知集合{2,3,6,8},{2,3},{2,6,8},U A B ===则()U A B =ð____________. 【参考答案】{6,8}109.已知集合{|2},{|13},A x x B x x A B =>=<<=则A.{|2}x x >B.{|1}x x > C.{|23}x x << D.{|13}x x << 【参考答案】C.110.已知集合{|(2)(1)0},{|10},M x x x N x x M N =+-<=+<=则A.(1,1)-B.(2,1)-C.(2,1)--D.(1,2) 【参考答案】C.111.已知全集{1,2,3,4,5,6,7,8},{1,3,5,7},{5,6,7},U M N ===则()U MN =ð A.{5,7} B.{2,4}C.{2,4,8}D.{1,3,5,6,7} 【参考答案】C.。

一、集合的概念及运算1. 集合的概念：集合是由确定的、互不相同的对象组成的整体。

其中，对象称为元素。

2. 集合的表示方法：集合可以用列举法、描述法和图示法来表示。

（1）列举法：将集合中的元素一一列举出来，用花括号{}括起来。

例如：A={1, 2, 3, 4}，表示集合A由元素1、2、3、4组成。

（2）描述法：用语言描述集合中元素的性质。

例如：B={x | x是2的倍数，且x小于10}，表示集合B由所有小于10的2的倍数组成。

（3）图示法：用Venn图或韦恩图表示集合之间的关系。

3. 集合的运算：（1）并集：将两个集合中的元素合并在一起，组成一个新的集合。

例如：C={5, 6, 7}，D={6, 7, 8}，则C∪D={5, 6, 7, 8}。

（2）交集：找出两个集合中共有的元素，组成一个新的集合。

例如：C={5, 6, 7}，D={6, 7, 8}，则C∩D={6, 7}。

（3）补集：在全集U中，不属于集合A的元素组成的集合称为A的补集，记作A'。

例如：A={1, 2, 3}，全集U={1, 2, 3, 4, 5}，则A'={4, 5}。

（4）差集：找出两个集合中属于第一个集合但不属于第二个集合的元素，组成一个新的集合。

例如：C={5, 6, 7}，D={6, 7, 8}，则C-D={5}。

二、集合的应用1. 集合在数列中的应用：集合可以用来表示数列，研究数列的性质。

例如：数列{an}的通项公式为an=n^2，则数列{an}可以表示为集合A={n^2 | n为正整数}。

2. 集合在函数中的应用：集合可以用来表示函数的定义域和值域。

例如：函数f(x)=x^2的定义域为R（实数集），值域为[0，+∞）。

3. 集合在几何中的应用：集合可以用来表示几何图形中的点、线、面等元素。

例如：直线l上的所有点组成的集合记作L。

三、高考数学试卷中集合的常见题型1. 集合的概念及运算：考察对集合概念的理解，以及集合运算的掌握。

高考考到集合的题目可以分为三大类：
①函数性质填空题，考察函数基本性质（单调性、奇偶性），一般是二次函数或指对数函数；
②解答题：函数应用题，需要根据题意列出函数关系求最值或其他值的题目，可能涉及到二次函数、指对数函数、三角函数等；
③解答题：函数性质综合题，函数性质的综合应用，可能涉及到二次函数、指对数函数、三角函数等，并且6年中有4年都是和导数求最值有关.都会涉及到对参数的分类讨论.
后两类综合性较强，可能大家目前能力还解决不了，可以重点关注第一部分，填空基本和期中考试难度类似.。

2016年高考数学试题分类汇编——集合1000字2016年高考数学试题分类汇编——集合本文将对2016年高考数学试题中与集合相关的题型进行汇编和分类，以供参考。

一、集合的概念与表示命题：若A＝{a1，a2，a3，a4，a5}，B＝{a2，a4，a6}，则A∩B＝（）．分析：本题考查集合的交集运算，交集的定义是同时属于两个集合的元素组成的集合。

根据A和B的定义，交集应该是A和B中共有的元素a2和a4。

故答案为{a2，a4}。

二、常用集合命题：下列说法正确的是（）。

A. ϕ∈{ϕ}，B. {ϕ}∈{ϕ}，C. ϕ∈{∅}，D. {∅}∈{∅}分析：本题考查对集合的理解和应用。

首先，空集ϕ不是任何集合的元素，所以A选项是错误的；其次，{ϕ}中唯一的元素是空集ϕ，所以B选项正确；再次，∅是包含0个元素的集合，所以C选项错误，最后，{∅}包含一个元素∅，所以D选项错误。

综上，正确答案为选项B。

三、集合的运算命题：已知集合A＝{1，2，3，4}，B＝{3，4，5，6}，则A∩B和A∪B的并集是（）．分析：本题考查集合的并集和交集的运算，先求出它们的值：A∩B＝{3，4}，A∪B＝{1，2，3，4，5，6}。

由于集合间的交集和并集也是集合，因此它们的并集为{1，2，3，4，5，6}，答案为选项D。

四、集合的运算律命题：已知集合S＝{x|x＜0}，T＝{x|x²-4x＋4≥0}，则S-T＝（）．分析：本题考查集合的补集运算，集合S包含所有小于0的实数，而集合T满足x²-4x＋4≥0，化简可得（x-2）²≥0，因此T包含所有实数。

因此，S和T的补集分别是{ x | x ≥ 0}和ϕ。

所以，S-T＝S∩Tc＝{ x | x < 0 }∩{ x | x ≥ 0 }c＝{ x | x < 0 }，选项A为正确答案。

五、应用题命题：一某餐厅启动了一次优惠活动，现有5000张100元代金券、4000张50元代金券及3000张20元代金券，若张三要使用3000元代金券，而这些代金券不可兑换成现金，求他最少需要换取几张代金券？分析：本题考查实际问题中集合的应用。