第八章常用试验设计的方差分析
- 格式:doc
- 大小:116.50 KB
- 文档页数:3


实验设计的方差分析与正交试验一、实验设计中的方差分析方差分析(analysis of variance,ANOVA)是一种统计方法,用于比较不同组之间的均值差异是否具有统计学上的显著性。
在实验设计中,方差分析主要被用来分析因变量(dependent variable)在不同水平的自变量(independent variable)中的变化情况。
通过比较不同组之间的方差,判断是否存在显著差异,并进一步分析差异的原因。
1. 单因素方差分析单因素方差分析是最简单的方差分析方法,适用于只有一个自变量的实验设计。
该方法通过比较不同组之间的方差来判断各组均值是否有差异。
步骤如下:(1)确定研究目的,选择合适的因变量和自变量。
(2)设计实验,确定各组的样本个数。
(3)进行实验,并收集数据。
(4)计算各组的平均值和总平均值。
(5)计算组内方差和组间方差。
(6)计算F值,通过计算F值来判断各组均值是否有显著差异。
2. 多因素方差分析多因素方差分析是在单因素方差分析的基础上,增加了一个或多个自变量的情况下进行的。
这种方法可以用来分析多个因素对因变量的影响,并判断各因素的主效应和交互效应。
步骤如下:(1)确定研究目的,选择合适的因变量和多个自变量。
(2)设计实验,确定各组的样本个数。
(3)进行实验,并收集数据。
(4)计算各组的平均值和总平均值。
(5)计算组内方差、组间方差和交互方差。
(6)计算F值,通过计算F值来判断各组均值是否有显著差异。
二、正交试验设计正交试验设计是一种设计高效实验的方法,可以同时考虑多个因素和各个因素之间的交互作用,并通过较少的试验次数得到较准确的结果。
1. 正交表的基本原理正交表的设计是基于正交原理,即每个因素和其他所有因素的交互效应都是独立的。
通过正交表设计实验,可以确保各因素和交互作用在样本中能够均匀地出现,从而减少误差来源,提高实验结果的可靠性。
2. 正交试验设计的步骤(1)确定要研究的因素和水平。

方差分析与试验设计方差分析是一种通过比较不同组之间的变差来判断均值差异是否显著的统计方法。
它通常用于试验设计中,用于分析不同处理组间的均值差异是否显著,从而评估不同处理的效果。
试验设计是科学研究中的一项重要工作,旨在通过科学的方法来验证研究假设。
试验设计涉及确定适当的样本大小、确定控制组和实验组、识别并控制潜在的影响因素等。
好的试验设计能够最大程度地减少偏差,提高实验的可靠性和准确性。
在方差分析中,我们通常将变量分为因素变量和响应变量。
因素变量是试验设置的处理组,例如不同的药物剂量或不同的施肥量。
响应变量是实验结果,可以是连续变量(如体重、收益等)或分类变量(如治疗成功与否)。
方差分析的基本原理是计算组内变差与组间变差之比,通过比较比值与理论的F分布来判断差异是否显著。
如果比值较大,则表明组间差异显著,即不同处理组的均值差异明显。
在进行方差分析时,我们需要满足一些前提条件,如独立性、正态性和方差齐性。
如果数据不符合这些条件,我们可以应用一些转换方法或进行非参数检验来处理。
完全随机设计是最简单的试验设计方法之一,它将实验对象随机分配到不同的处理组中。
这种设计方法适用于研究变量之间没有任何关系的情况,其优点是简单易行,但缺点是可能存在一些潜在的影响因素未被控制。
随机区组设计是一种常用的试验设计方法,它将实验对象分组后再随机分配到不同的处理组中。
这种设计方法能够控制部分潜在因素的影响,并提高实验的可靠性和准确性。
Latin square设计是一种更加复杂的试验设计方法,它在随机区组设计的基础上增加了均衡性。
Latin square设计通过交叉安排处理组和区块,使得每个处理出现在每个区块中,从而进一步控制潜在因素的影响。
除了上述常见的试验设计方法外,还有其他一些高级试验设计方法,如因子分析设计、回归分析设计等。
这些方法可以根据实验的具体要求来选择和应用。
综上所述,方差分析和试验设计是统计学中重要的概念和方法。


第八章一般线性模型――General Linear Model菜单详解请注意,本章的标题用了一些修辞手法,一般线性模型可不是用一章就可以说清楚的,因为它包括的内容实在太多了。
那么,究竟我们用到的哪些分析会包含在其中呢?简而言之:凡是和方差分析粘边的都可以用他来做。
比如成组设计的方差分析(即单因素方差分析)、配伍设计的方差分析(即两因素方差分析)、交叉设计的方差分析、析因设计的方差分析、重复测量的方差分析、协方差分析等等。
因此,能真正掌握GLM菜单的用法,会使大家的统计分析能力有极大地提高。
实际上一般线性模型包括的统计模型还不止这些,我这里举出来的只是从用SPSS作统计分析的角度而言的一些。
好了,既然一般线性模型的能力如此强大,那么下属的四个子菜单各自的功能是什么呢?请看:∙Univariate子菜单:四个菜单中的大哥大,绝大部分的方法分析都在这里面进行。
∙Multivariate子菜单:当结果变量(应变量)不止一个时,当然要用他来分析啦!∙Repeted Measures子菜单:顾名思义,重复测量的数据就要用他来分析,这一点我可能要强调一下,用前两个菜单似乎都可以分析出来结果,但在许多情况下该结果是不正确的,应该用重复测量的分析方法才对(不能再讲了,再讲下去就会扯到多水平模型去了)。
∙Variance Components子菜单:用于作方差成份模型的,这个模型实在太深,不是一时半会说的请的,所以我在这里就干脆不讲了。
出于模型复杂性、篇幅、应用范围及乱七八糟一系列的理由,当然主要是我懒得一一解释,我决定本章采用举例讲解的方式,及讲解一些常见的分析实例,通过这种方法来熟悉那些最为常用的分析方法。
对统计分析的数据格式不太熟悉的朋友,请一定先去看看统计软件第一课:论统计软件中的数据录入格式,会大有帮助的。
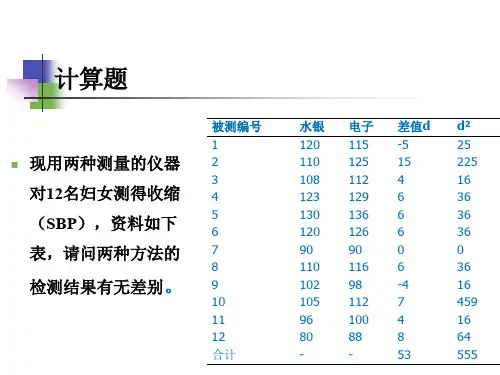
§8.1两因素方差分析下面的这个例子来自《卫生统计学》第四版,书还没有出来,大家先尝尝鲜。




方差分析与实验设计方差分析(Analysis of Variance,简称ANOVA)是一种统计方法,用于比较两个或多个样本均值之间的差异是否显著。
它是实验设计中常用的一种方法,可以帮助研究者确定实验结果是否受到不同因素的影响,并进一步分析这些因素对实验结果的贡献程度。
实验设计是科学研究中的重要环节,它涉及到如何选择实验对象、确定实验因素、设计实验方案等问题。
合理的实验设计可以提高实验的可靠性和有效性,减少误差的影响,从而得到更准确的结论。
方差分析与实验设计密切相关,下面将介绍方差分析的基本原理和实验设计的常用方法。
一、方差分析的基本原理方差分析的基本原理是通过比较组间变异与组内变异的大小来判断不同组别之间的均值是否存在显著差异。
具体步骤如下:1. 建立假设:首先,我们需要建立原假设和备择假设。
原假设通常是假设各组别之间的均值没有显著差异,备择假设则是假设各组别之间的均值存在显著差异。
2. 计算总平方和:总平方和是各观测值与总均值之差的平方和,表示了所有数据的总变异程度。
3. 计算组间平方和:组间平方和是各组均值与总均值之差的平方和,表示了不同组别之间的差异程度。
4. 计算组内平方和:组内平方和是各观测值与各组均值之差的平方和,表示了同一组别内部的差异程度。
5. 计算F值:F值是组间平方和与组内平方和的比值,用于判断组间差异是否显著。
如果F值大于临界值,则拒绝原假设,认为各组别之间的均值存在显著差异。
6. 进行事后比较:如果F值显著,我们可以进行事后比较,确定哪些组别之间存在显著差异。
二、实验设计的常用方法1. 完全随机设计:完全随机设计是最简单的实验设计方法,它要求实验对象随机分配到不同的处理组中。
这种设计方法适用于实验对象之间没有明显差异的情况。
2. 随机区组设计:随机区组设计是在完全随机设计的基础上引入区组因素,将实验对象分为若干个区组,然后在每个区组内进行随机分配。
这种设计方法可以减少误差的影响,提高实验的可靠性。
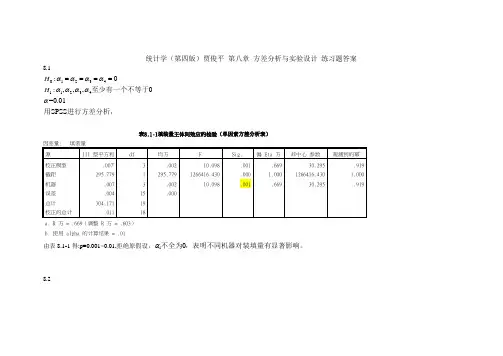
统计学(第四版)贾俊平 第八章 方差分析与实验设计 练习题答案8.10123411234:0:,,,0=0.01SPSS H H ααααααααα====至少有一个不等于用进行方差分析,表8.1-1填装量主体间效应的检验(单因素方差分析表)因变量: 填装量 源 III 型平方和df均方F Sig.偏 Eta 方非中心 参数观测到的幂b校正模型 .007a3 .002 10.098 .001 .669 30.295 .919 截距 295.7791 295.7791266416.430.000 1.000 1266416.4301.000 机器 .007 3 .002 10.098.001.66930.295.919误差 .004 15 .000总计 304.17119 校正的总计.01118a. R 方 = .669(调整 R 方 = .603)b. 使用 alpha 的计算结果 = .01由表8.1-1得:p=0.001<0.01,拒绝原假设,i 0α不全为,表明不同机器对装填量有显著影响。
8.201231123:0:,,0=0.05SPSS H H ααααααα===至少有一个不等于用进行方差分析,表8.2-1满意度评分主体间效应的检验(单因素方差分析表)因变量: 评分 源III 型平方和df 均方 F Sig.校正模型 29.610a2 14.805 11.756 .001 截距 975.156 1 975.156 774.324 .000 管理者 29.610 2 14.805 11.756.001误差 18.890 15 1.259总计 1061.000 18 校正的总计48.50017a. R 方 = .611(调整 R 方 = .559)由表8.2-1得:p=0.001<0.05,拒绝原假设,i 0α不全为,表明管理者水平不同会导致评分的显著差异。
8.301231123:0:,,0=0.05SPSS H H ααααααα===至少有一个不等于用进行方差分析,表8.3-1电池寿命主体间效应的检验(单因素方差分析表)因变量: 电池寿命 源III 型平方和df 均方 F Sig. 偏 Eta 方 非中心 参数 观测到的幂b校正模型 615.600a2 307.800 17.068 .000 .740 34.137 .997 截距 22815.000 1 22815.000 1265.157 .000 .991 1265.157 1.000 企业 615.600 2 307.800 17.068.000.74034.137.997误差 216.400 12 18.033总计 23647.000 15 校正的总计832.00014a. R 方 = .740(调整 R 方 = .697)b. 使用 alpha 的计算结果 = .05由表8.2-1得:p=0.001<0.05,拒绝原假设,i 0α不全为,表明3个企业生产的电池平均寿命之间存在显著差异。
统计学(第四版)贾俊平 第八章 方差分析与实验设计 练习题答案8.10123411234:0:,,,0=0.01SPSS H H ααααααααα====至少有一个不等于用进行方差分析,表8.1-1填装量主体间效应的检验(单因素方差分析表)因变量: 填装量 源 III 型平方和df均方F Sig.偏 Eta 方非中心 参数观测到的幂b校正模型 .007a3 .002 10.098 .001 .669 30.295 .919 截距 295.7791 295.7791266416.430.000 1.000 1266416.4301.000 机器 .007 3 .002 10.098.001.66930.295.919误差 .004 15 .000总计 304.17119 校正的总计.01118a. R 方 = .669(调整 R 方 = .603)b. 使用 alpha 的计算结果 = .01由表8.1-1得:p=0.001<0.01,拒绝原假设,i 0α不全为,表明不同机器对装填量有显著影响。
8.201231123:0:,,0=0.05SPSS H H ααααααα===至少有一个不等于用进行方差分析,表8.2-1满意度评分主体间效应的检验(单因素方差分析表)因变量: 评分 源III 型平方和df 均方 F Sig.校正模型 29.610a2 14.805 11.756 .001 截距 975.156 1 975.156 774.324 .000 管理者 29.610 2 14.805 11.756.001误差 18.890 15 1.259总计 1061.000 18 校正的总计48.50017a. R 方 = .611(调整 R 方 = .559)由表8.2-1得:p=0.001<0.05,拒绝原假设,i 0α不全为,表明管理者水平不同会导致评分的显著差异。
8.301231123:0:,,0=0.05SPSS H H ααααααα===至少有一个不等于用进行方差分析,表8.3-1电池寿命主体间效应的检验(单因素方差分析表)因变量: 电池寿命 源III 型平方和df 均方 F Sig. 偏 Eta 方 非中心 参数 观测到的幂b校正模型 615.600a2 307.800 17.068 .000 .740 34.137 .997 截距 22815.000 1 22815.000 1265.157 .000 .991 1265.157 1.000 企业 615.600 2 307.800 17.068.000.74034.137.997误差 216.400 12 18.033总计 23647.000 15 校正的总计832.00014a. R 方 = .740(调整 R 方 = .697)b. 使用 alpha 的计算结果 = .05由表8.2-1得:p=0.001<0.05,拒绝原假设,i 0α不全为,表明3个企业生产的电池平均寿命之间存在显著差异。
第八章 常用试验设计的方差分析
8.1 多因素随机区组试验和单因素随机区组试验的分析方法有何异同?多因素随机区组试验处理项的自由度和平方和如何分解?怎样计算和测验因素效应和互作的显著性,正确地进行水平选优和组合选优?
8.2 裂区试验和多因素随机区组试验的统计分析方法有何异同?在裂区试验中误差E a 和E b 是如何计算的,各具什么意义?如何估计裂区试验中的缺区?裂区试验的线性模型是什么?
8.3 有一大豆试验,A 因素为品种,有A 1、A 2、A 3、A 4 4个水平,B 因素为播期,有B 1、B 2、B 3 3个水平,随机区组设计,重复3次,小区计产面积25平方米,其田间排列和产量(kg )如下图,试作分析。
区组Ⅰ
区组Ⅱ
区组Ⅲ [答案:
e
MS
0.31,F 测验:品种、播期极显著,品种×播期不显著]
8.4 有一小麦裂区试验,主区因素A ,分A1(深耕)、A2(浅)两水平,副区因素B ,分B1(多肥)、B2(少肥)两水平,重复3次,小区计产面积15平方米,其田间排列和产量(假设数字)如下图,试作分析。
区组Ⅰ
区组Ⅱ
区组Ⅲ
[答案:
a
E MS
=0.58,
b
E MS
=2.50,F 测验:A 和B 皆显著,A ×B 不显著]
8.5 设若上题小麦耕深与施肥量试验为条区设计,田间排列和产量将相应如下图,试作分
析,并与裂区设计结果相比较)。
B 1 B 1B 2 B 2
B 2B 1
[答案:
A
E MS
=0.58,
B
E MS
=1.75,
c
E MS
=3.25,F 测验A 、B 均显著,A ×B 不显著]
8.6 江苏省淮南地区夏大豆区域试验部分资料摘录如下:
试点 年份 区组 CK 19—15 31—15 4—1 21—16 试点1 1977年
Ⅰ 134 160 168 226 196 Ⅱ 146 180 156 170 190 Ⅲ 148 206 188 216 200 1978年
Ⅰ 220 264 280 212 168 Ⅱ 228 260 276 208 156 Ⅲ 208 220 300 260 148 试点2 1977年
Ⅰ 137 236 197 196 155
Ⅱ 173 207 178 192 179 Ⅲ 110 171 223 208 125 1978年
Ⅰ 179 201 150 195 186
Ⅱ 182 224 189 203 191
Ⅲ
207
262
187
210
183
各年各点均为随机区组设计,试分析此试验结果。
[答案:
2
=3.67,e MS =406.06,Fv=12.89,Fvs=1.88,Fvy=5.18,Fvsy=10.35]
8.7 在药物处理大豆种子试验中,使用了大中小三种类型种子,分别用五种浓度、两种处理时间进行试验处理,播种后45天对每种各取两个样本,每个样本取10株测定其干物重,求其平均数,结果如下表。
试进行方差分析。
处理时间A 种子类型C 浓度B
B 1(0×10-6)
B 2(10×10-6) B 3(20×10-6) B 4(30×10-6) B 5(40×10-6)
A 1(12小时) C 1(小粒)
7.0 12.8 22.0 21.3 24.4
6.5 11.4 21.8 20.3 23.2 C 2(中粒)
13.5 13.2 20.4 19.0 24.6 13.8 14.2 21.4 19.6 23.8 C 3(大粒)
10.7 12.4 22.6 21.3 24.5
10.3 13.2 21.8 22.4 24.2 A 2(24小时) C 1(小粒)
3.6
10.7 4.7 12.4 13.6
1.5
8.8
3.4
10.5
13.7
C2(中粒) 4.7 9.8 2.7 12.4 14.0
4.9 10.5 4.2 13.2 14.2
C3(大粒) 8.7 9.6 3.4 13.0 14.8
3.5 9.7
4.2 12.7 12.6
[答案:B因素显著]
8.8 为了研究湿度和温度对粘虫卵发育历期的影响,用3种湿度、4种温度处理粘虫卵,采用随机区组设计,重复4次,结果如下表,试进行方差分析。
相对湿度(%) 温度(℃)
历期
1 2 3 4
100 26 93.2 91.2 90.7 92.2
28 87.6 85.7 84.2 82.4
30 79.2 74.5 79.3 70.4
32 67.7 69.3 67.6 68.1
70 26 89.4 88.7 86.3 88.5
28 86.4 85.3 86.7 84.2
30 77.2 76.3 74.5 75.7
32 70.1 72.1 70.3 69.5
40 26 99.9 99.2 93.3 94.5
28 91.3 94.6 92.3 91.4
30 82.7 81.3 84.5 86.8
32 75.3 74.1 72.3 71.4
[答案:湿度、温度间差异显著,湿度与温度互作显著,误差均方3.86]
8.9 有一施肥试验,N素4个水平,P、K肥料均为时施肥与不施肥(O)两种水平采用正交表为L8(4×24)的正交设计,小区面积20m2,重复3次,随机区组排列,试验结果如下。
试作分析。