全等三角形判定(一)

全等三角形的判定一1．理解和掌握全等三角形判定方法1——“边边边”，和判定方法2——“边角边”；2．能把证明一对角或线段相等的问题，转化为证明它们所在的两个三角形全等.一、全等三角形判定1——“边边边”三边对应相等的两个三角形全等.（可以简写成“边边边”或“SSS”）.要点诠释：如图，如果''A B＝AB，''A C＝AC，''B C＝BC，则△ABC△△'''A B C.二、全等三角形判定2——“边角边”1.全等三角形判定2——“边角边”两边和它们的夹角对应相等的两个三角形全等（可以简写成“边角边”或“SAS”）.要点诠释：如图，如果AB ＝''A B，△A＝△'A，AC ＝''A C，则△ABC△△'''A B C. 注意：这里的角，指的是两组对应边的夹角.2. 有两边和其中一边的对角对应相等，两个三角形不一定全等.如图，△ABC与△ABD中，AB＝AB，AC＝AD，△B＝△B，但△ABC与△ABD不完全重合，故不全等，也就是有两边和其中一边的对角对应相等，两个三角形不一定全等.教学目标学习内容知识梳理类型一、全等三角形的判定1——“边边边”例1、如图，在△ABC 和△ADE 中，AB ＝AC ，AD ＝AE ，BD ＝CE ，求证：△BAD ＝△CAE.【答案与解析】证明：在△ABD 和△ACE 中，AB AC AD AE BD CE =⎧⎪=⎨⎪=⎩△△ABD△△ACE （SSS ）△△BAD ＝△CAE （全等三角形对应角相等）.【变式】已知：如图，AD ＝BC ，AC ＝BD.试证明：△CAD ＝△DBC.证明：连接DC ，在△ACD 与△BDC 中()AD BC AC BDCD DC ⎧=⎪=⎨⎪=⎩公共边 △△ACD△△BDC （SSS ）△△CAD ＝△DBC （全等三角形对应角相等）类型二、全等三角形的判定2——“边角边”例2、如图，AD 是△ABC 的中线，求证：AB ＋AC ＞2AD ．证明：如图，延长AD 到点E ，使AD ＝DE ，连接CE ．在△ABD 和△ECD 中，AD ＝DE ，△ADB ＝△EDC ，BD ＝CD ．△△ABD△△ECD ．△AB ＝CE ．△AC ＋CE ＞AE ，△AC ＋AB ＞AE ＝2AD ．即AC ＋AB ＞2AD ．例3、已知，如图：在△ABC 中，△B ＝2△C ，AD△BC ，求证：AB ＝CD －BD ． 证明：在DC 上取一点E ，使BD ＝DE例题讲解△ AD△BC ，△△ADB ＝△ADE在△ABD 和△AED 中， BD ＝DE ，AD ＝AD ．△△ABD△△AED （SAS ）．△AB ＝AE ，△B ＝△AED ．又△△B ＝2△C ＝△AED ＝△C ＋△EAC ．△△C ＝△EAC ．△AE ＝EC ．△AB ＝AE ＝EC ＝CD—DE ＝CD—BD ． 【变式】已知，如图，在四边形ABCD 中，AC 平分△BAD ，CE△AB 于E ，并且AE ＝21（AB ＋AD ），求证：△B ＋△D ＝180°.证明：在线段AE 上，截取EF ＝EB ，连接FC ，△CE△AB ，△△CEB ＝△CEF ＝90°在△CBE 和△CFE 中，CEB CEF EC =EC EB EF =⎧⎪∠=∠⎨⎪⎩△△CBE△△CFE （SAS ）△△B ＝△CFE△AE ＝21（AB ＋AD ），△2AE ＝ AB ＋AD △AD ＝2AE －AB△AE ＝AF ＋EF ，△AD ＝2（AF ＋EF ）－AB ＝2AF ＋2EF －AB ＝AF ＋AF ＋EF ＋EB －AB ＝AF ＋AB －AB ，即AD ＝AF在△AFC 和△ADC 中(AF AD FAC DAC AC AC =⎧⎪∠=∠⎨⎪=⎩角平分线定义）△△AFC△△ADC （SAS ）△△AFC ＝△D△△AFC ＋△CFE ＝180°，△B ＝△CFE.A E D CB△△AFC ＋△B ＝180°，△B ＋△D ＝180°.类型三、全等三角形判定的实际应用例4、如图，公园里有一条“Z 字形道路ABCD ，其中AB△CD ，在AB ，BC ，CD 三段路旁各有一个小石凳E ，M ，F ，且BE ＝CF ，M 在BC 的中点.试判断三个石凳E ，M ，F 是否恰好在一条直线上？为什么？证明：△AB 平行CD （已知）∴∠B ＝∠C （两直线平行，内错角相等）∵M 在BC 的中点（已知）∴BM ＝CM （中点定义）在△BME 和△CMF 中BE CF B C BM CM =⎧⎪∠=∠⎨⎪=⎩∴△BME ≌△CMF （SAS ）∴∠EMB ＝∠FMC （全等三角形的对应角相等）∴∠EMF ＝∠EMB ＋∠BMF ＝∠FMC ＋∠BMF ＝∠BMC ＝180°（等式的性质）∴E ，M ，F 在同一直线上 一、选择题 1. 如图，已知AB ＝AC ，D 为BC 的中点，结论：△AD△BC ；△AD 平分△BAC ；△△B ＝△C ；△△ABC 是等边三角形.其中正确的是（ ）.A.△△B. △△C. △△△D. △△2．如图，是的中线，、分别是和延长线上的点，且，连接、，下列说法：△；△ 和的面积相等；△；△ △，其中正确的有（ ）．A.1个B.2个AD ABC ∆E F AD AD DE DF =BF CE CE BF =ABD ∆ACD ∆//BF CE BDF ∆CDE ∆综合题库C.3个D.4个3. AD为△ABC中BC边上的中线, 若AB＝2, AC＝4, 则AD的范围是( )A .AD＜6 B. AD＞2 C. 2＜AD＜6 D. 1＜AD＜34．如图，AB＝DC，AD＝BC，E、F是DB上两点，且BF＝DE，若△AEB＝120°，△ADB＝30°，则△BCF ＝（）．A.150°B.40°C.80°D.90°5. 根据下列条件能唯一画出△ABC的是（）A.AB＝3，BC＝4，AC＝8B.AB＝4，BC＝3，△A＝30°C.AB＝5，AC＝6，△A＝45°D. △A＝30°，△B＝60°，△C＝90°6. 如图，在△ABC中，△A＝50°，△B＝△C，点D，E，F分别在AB，BC，AC上，并且BD＝CE，BE＝CF，则△DEF等于（）A.50°B.60°C. 65°D. 70°二、填空题7. 如图，AB＝CD，AC＝DB，△ABD＝25°，△AOB＝82°，则△DCB＝_________.8. 如图，△ABC是三边均不等的三角形，DE＝BC，以D、E为两个顶点画位置不同的三角形，使所作的三角形与△ABC全等，这样的三角形最多可以画个.9. 如图，已知AE＝AF，AB＝AC，若用“SAS”证明△AEC△AFB，还需要条件.10. 如图，在四边形ABCD中，对角线AC、BD互相平分，则图中全等三角形共有_____对.11. 如图所示，BE△AC于点D，且AD＝CD，BD＝ED，若△ABC＝54°，则△E＝°.AA BB的中点连在一起，可以做成一个测量工件内槽宽的工具（卡钳），如图，若测得12. 把两根钢条','AB＝5厘米，则槽宽为厘米．三、解答题13. 如图，将两个一大、一小的等腰直角三角尺拼接（A、B、D三点共线，AB＝CB，EB＝DB，△ABC＝△EBD＝90°），连接AE、CD，试确定AE与CD的位置与数量关系，并证明你的结论．14. 如图, ∠B ＝∠C, BD ＝CE, CD ＝BF 。

1.2 直角三角形全等的判定（一）
学习目标
1、用“斜边、直角边”法判定两个直角三角形全等.
2、证明直角三角形全等的HL 判定定理. 学习重点
直角三角形HL 全等判定定理. 学习难点
通过HL 全等判定定理来解决实际问题，体会数学的应用. 学习过程 一、自学质疑：
操作与思考：如图Rt △ABC,画Rt △A ，B ，C ，，使斜边AB= A ，B ，，直角边AC= A ，C ，，这两个三角形全等吗？
二、互动交流： HL 定理： 已知： 求证： 证明：
三、精讲点拨：
1、证明:在直角三角形中，300所对的直角边等于斜边的一半。

2、如图，CD ⊥AB,BE ⊥AC,垂足分别是D 、E, BE 、CD 相交于点O ，如果AB=AC ，哪么图中有几对全等的直角三角形？取其中的一对予以证明。

四、巩固迁移
1、已知：如图，AB=CD,AE⊥BD,CF ⊥BD,垂足分别为E、F，且BF=DE. 求证：∠ABD= ∠CDB.。

授课时间： 年 月 日 课题：三角形全等的判定（一） 备课教师： 杨国林 授课教师： 姓名： 审批人： 导学案编号：2016 8ss11010013一、导 课：在学生已经学习了全等三角形的概念和性质的基础上，探究三角形全等的条件设计意图及调整改明确教学目标、重难点二、课堂目标： 1．三角形全等的“边边边”的条件．2．了解三角形的稳定性．3．经历探索三角形全等条件的过程，体会利用操作、•归纳获得数学结论的过程．开始上课： 三、共同探索(一)．回顾思考： 1．（1）三角形中已知三个元素，包括哪几种情况？ 三个角、三个边、两边一角、两角一边． (二)、新课1. 回忆前面研究过的全等三角形． 已知△ABC ≌△A ′B ′C ′，找出其中相等的边与角． 图中相等的边是：AB=A ′B 、BC=B ′C ′、AC=A ′C ． 相等的角是：∠A=∠A ′、∠B=∠B ′、∠C=∠C ′．2.已知三角形△ABC 你能画一个三角形与它全等吗？怎样画？阅读教材P35-36归纳：三边对应相等的两个三角形全等，简写为“边边边”或“SSS ”．书写格式: 在△ABC 和△A 1B 1C 1中____________________________________________________________________ ∴ △ABC ≌△A 1B 1C 1（SSS ）C 1B 1CABA 13. 小组合作学习（1）如图，△ABC 是一个钢架，AB=AC ，AD 是连结点A 与BC 中点D 的支架．求证：△ABD ≌△ACD ． 证明：∵D 是BC 的中点∴__________________________ 在△ABD 和△ACD 中(AB ACBD CD AD AD =⎧⎪=⎨⎪=⎩公共边)∴△___________≌△_____________ ( ) 4、用尺规作一个角等于已知角已知：∠AOB ．求作： ∠A ′O ′B ′=∠AOB ．D CB A五、强化训练【A】组1．三边对应相等的两个三角形________(可简写成“________”或“________”)．2．三角形的三边的长度确定了，这个三角形的________和________就完全确定了．知识点1：用“SSS”判定三角形全等1．如图，已知AB＝AD，AC＝AE，BC＝DE，则下列结论正确的是()A．△AEF≌△ACD B．△ADF≌△ADBC．△ABC≌△ADE D．△AEF≌△CDF2．如图，在△ABC中，AB＝AC，BE＝CE，则由“SSS”可以直接判定()A．△ABD≌△ACD B．△BDE≌△CDEC．△ABE≌△ACE D．以上都不对3．如图，AD＝BC，AC＝BD，用三角形全等的判定“边边边”可证明________≌________或________≌________. 【B】组4．如图，AF＝CD，AB＝ED，EF＝BC，那么△ABC≌△DEF的理由是________．5．如图，已知AB＝CD，若根据“SSS”证得△ABC≌△CDA，需要添加一个条件是________．6．如图，AB＝AC，DB＝DC，EB＝EC.(1)图中有几对全等三角形？请一一写出来；(2)选择(1)中的一对全等三角形加以证明．【C】组7．如图，已知AB＝AC，DB＝EC，AD＝AE，∠1＝25°，则∠2＝________.。

《三角形全等的判定（一）》磨课计划磨课计划讨论记录：合作学习中如何做到：1、提高“小组合作学习”的时效性。

2、解决教学过程中存在的许多不足，如后进生在小组合作学习的热情不高，优生吃不饱现象，部分学生在小组合作时浮于表面、流于形式等。

3、把握好教师的主导作用，既不能过于干预学生思考讨论，又不能游离于学生之外。

张俊芳：课堂上营造一个宽松和谐的学习氛围，充分调动学生学习的积极性、主动性。

让全体同学在感觉说错了也不要紧的情况下大胆发言。

张新华：得关注后进生，多鼓励、多表扬。

同时充分调动学生的学习积极性，激发学生学习兴趣，还要培养学生善于发现、分析、解决和运用数学的能力。

崔宝卫：发现后进生的优点就把优点放大，增加后进生的信心。

多给后进生一些关爱，让他们觉得老师和同学们都关注真自己。

赵庆山：在小组合作探讨的问题选择上需要关注学生之间存在的差异，关注学困生，提供不同的学生都可以发挥的空间，有不同的要求和指导。

利光辉：可以用较为简单的问题，让后进生来回答，增强自信。

发动全班同学多帮助后进生。

李芹：在教学活动中，我们要明确学生是课堂的主角，是活动的参与者，在一定程度上还是活动的组织者和设计者，在小组合作学习中，学生为主体教师为辅。

秦成娟：教师要大胆放手给学生，让他们多说、多练、多发表意见和建议，要多鼓励基础薄弱、参与不积极、思维不敏捷的学生多发言黄学利：为了使合作学习收到实效，而不是“形式化”，“合作时间”的安排也很关键。

然而在教学和研究中，我们经常发现有的教师为了完成教学内容，担心时间不够，结果刚开始的小组合作讨论，学生刚进入角色，便让学生汇报，成了简单的教师“导”，学生“演”，当然结果也就成了“导”不明，“演”不精。

每次合作学习，教师都一定要留给学生充足的时间，让每个小组的成员都有独立思考的余地，有交流的尝试。

张俊芳：自主学习的中心在学生，在于学生之间的互动和交往，教师在教学中应发挥主导作用，要敢于放手给学生。

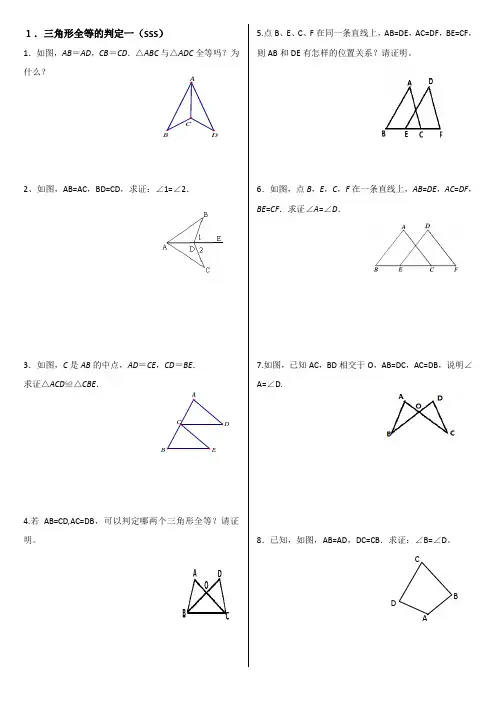
１．三角形全等的判定一（SSS ）1．如图，AB ＝AD ，CB ＝CD ．△ABC 与△ADC 全等吗？为什么？2、如图，AB=AC ，BD=CD ，求证：∠1=∠2．3．如图，C 是AB 的中点，AD ＝CE ，CD ＝BE ． 求证△ACD ≌△CBE ．4.若AB=CD,AC=DB ，可以判定哪两个三角形全等？请证明。

5.点B 、E 、C 、F 在同一条直线上，AB=DE ，AC=DF ，BE=CF ，则AB 和DE 有怎样的位置关系？请证明。

6．如图，点B ，E ，C ，F 在一条直线上，AB =DE ，AC =DF ，BE =CF ．求证∠A =∠D ．7.如图，已知AC ，BD 相交于O ，AB=DC ，AC=DB ，说明∠A=∠D.8．已知，如图，AB=AD ，DC=CB ．求证：∠B=∠D 。

ADCBFED BA9．如图, AD ＝BC, AB ＝DC, DE ＝BF. 求证：BE ＝DF.10.已知如图，A 、E 、F 、C 四点共线，BF=DE ，AB=CD. ⑴请你添加一个条件，使△DEC ≌△BFA ； ⑵在⑴的基础上，求证：DE ∥BF.11.如图，△ABC 中，AD=AE ， BE=CD ，AB=AC ，说明△ABD ≌△ACE12.如图，AC 与BD 交于点O ，AD=CB ，E 、F 是BD 上两点，且AE=CF ，DE=BF.请推导下列结论：⑴∠D=∠B ；⑵AE ∥CF ．13.如图,ABC ∆≌△ADE ，BC 的延长线交DA 于F ，交DE于G, ∠AED=105°∠CAD=10°∠B=25°求∠DFB 、∠DGB 的度数.14.．证明：如果两个三角形有两条边和第三边上的中线对应相等，那么这两个三角形全等．２．三角形全等的判定二（SAS ）1．如图，AC 和BD 相交于点O ，OA =OC ，OB =OD ．求证DC ∥AB ．2．如图，△ABC ≌△A B C '''，AD ，A D ''分别是△ABC ，△A B C '''的对应边上的中线，AD 与A D ''有什么关系？证明你的结论．3．如图，已知AC ⊥AB ，DB ⊥AB ，AC ＝BE ，AE ＝BD ，试猜想线段CE 与DE 的大小与位置关系，并证明你的结论．4．已知：如图，AD ∥BC ，AD=CB ，求证：△ADC ≌△CBA ．5．已知：如图AD ∥BC ，AD=CB ，AE=CF 。

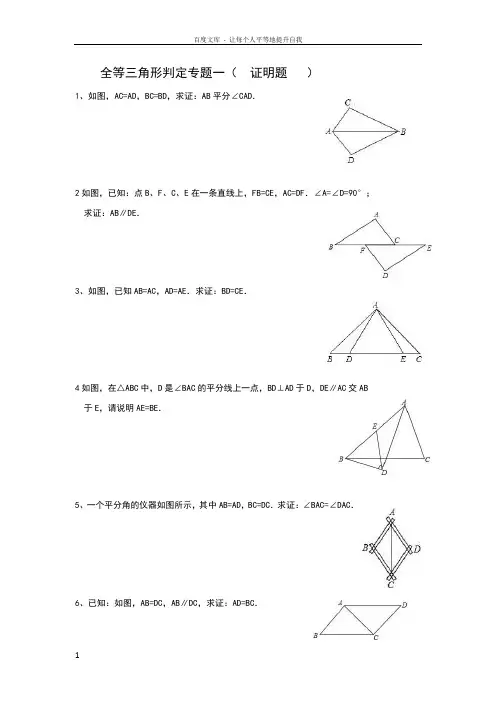
全等三角形判定专题一（证明题）1、如图，AC=AD，BC=BD，求证：AB平分∠CAD．2如图，已知：点B、F、C、E在一条直线上，FB=CE，AC=DF．∠A=∠D=90°；求证：AB∥DE．3、如图，已知AB=AC，AD=AE．求证：BD=CE．4如图，在△ABC中，D是∠BAC的平分线上一点，BD⊥AD于D，DE∥AC交AB 于E，请说明AE=BE．5、一个平分角的仪器如图所示，其中AB=AD，BC=DC．求证：∠BAC=∠DAC．6、已知：如图，AB=DC，AB∥DC，求证：AD=BC．7、如图：点C是AE的中点，∠A=∠ECD，AB=CD，求证：∠B=∠D．8、如图，BD⊥AC于点D，CE⊥AB于点E，AD=AE．求证：BE=CD．9、如图所示，已知AE⊥AB，AF⊥AC，AE=AB，AF=AC．求证：EC=BF．10、已知：如图，点E、F在AD上，且AF=DE，∠B=∠C，AB∥DC．求证：AB=DC．11已知：如图，CB⊥AD，AE⊥DC，垂足分别B、E，AE、BC相交于点F，且AB=BC．求证：△ABF≌△CBD．12、如图，已知，△ABC和△ADE均为等边三角形，BD、CE交于点F．（1）求证：BD=CE；（2）求锐角∠BFC的度数．、13、如图，在△ABC中，AB=AC，点D、E、F分别在BC、AB、AC边上，且BE=CF，BD=CE．（1）求证：△DEF是等腰三角形；（2）当∠A=40°时，求∠DEF的度数；（3）△DEF可能是等腰直角三角形吗？为什么？14、已知：如图，AB∥CD，AB=CD，点B、E、F、D在同一直线上，∠A=∠C．求证：（1）AE=CF；（2）AE∥CF．15、如图所示，已知AE⊥AB，AF⊥AC，AE=AB，AF=AC．求证：（1）EC=BF；（2）EC⊥BF．16：已知：AB=4，AC=2，D 是BC 中点， AD 是整数，求AD 长。

八年级上册数学《第十二章 全等三角形》1.2.2 三角形全等的判定（一）“边边边”与“边角边”◆利用“SSS ”判定两个三角形全等文字语言：三边分别相等的两个三角形全等，简写为“边边边”或“SSS”.几何语言：在△ABC 和△DEF 中，AB =DE BC =EF CA =FD∴△ABC ≌△DEF (SSS).◆利用“SAS ”判定两个三角形全等1、文字语言：两边和它们的夹角分别相等的两个三角形全等，简写成“边角边”或“SAS”.2、几何语言：在△ABC 和△DEF 中，AB =DE ∠B =∠E BC =EF∴△ABC ≌△DEF (SSS).3、方法：（1）已知两边，可以找“夹角”；（2）已知一角和这角的一夹边，可找这角的另一夹边【注意】1. 有两边和其中一边的对角对应相等的两个三角形不一定全等.2. 说明两三角形全等所需的条件应按对应边的顺序书写.3. 结论中所出现的边必须在所证明的两个三角形中.【例题1】如图，△ABC 中，AB ＝AC ，EB ＝EC ，则由“SSS ”可以判定（ ）A．△ABE≌△ACE B．△ABD≌△ACDC．△BDE≌△CDE D．以上答案都不对【变式1-1】如图，在△ACE和△BDF中，AE＝BF，CE＝DF，要利用“SSS”证明△ACE≌△BDF，需添加的一个条件可以是（ ）A．AB＝BC B．DC＝BC C．AB＝CD D．以上都不对【变式1-2】下列四个三角形中，与图中的△ABC全等的是（ ）A．B．C ．D ．【变式1-3】如图，已知点A 、D 、B 、F 在一条直线上，AC ＝EF ，AD ＝FB ，要使△ABC ≌△FDE ，还需添加一个条件，这个条件可以是（ ）A ．AC ∥EFB ．∠E ＝∠C C ．∠ABC ＝∠FDED ．AB ＝DF【变式1-4】如图，已知∠1＝∠2，若用“SAS ”证明△BDA ≌△ACB ，还需加上条件（ ）A ．AD ＝BCB ．BD ＝AC C ．∠D ＝∠C D ．OA ＝OB【例题2】如图，已知点B ，C ，D ，E 在同一直线上，且AB ＝AE ，AC ＝AD ，BD ＝CE ．求证：△ABC ≌△AED．【变式2-1】（2023•云南）如图，C是BD的中点，AB＝ED，AC＝EC．求证：△ABC≌△EDC．【变式2-2】如图，AB＝DE，AC＝DF，BF＝EC，△ABC和△DEF全等吗？请说明理由．【变式2-3】（2023•永善县三模）如图，AB＝DE，AC＝DF，BE＝CF，求证：△ABC≌△DEF．【例题3】11．（2018秋•庆云县校级月考）请仔细观察用直尺和圆规作一个角等于已知角的示意图，请你根据所学的三角形全等有关的知识，说明画出∠A ′O ′B ′＝∠AOB 的依据是 ．【变式3-1】小聪在用直尺和圆规作一个角等于已知角时，具体过程是这样的：已知：∠AOB ．求作：∠A ′O ′B ′，使∠A ′O ′B ′＝∠AOB ．作法：（1）如图，以点O 为圆心，任意长为半径画弧，分别交OA ，OB 于点C ，D ；（2）画一条射线O ′A ′，以点O ′为圆心，OC 长为半径画弧，交O ′A ′于点C ′；（3）以点C '为圆心，CD 长为半径画弧，与第（2）步中所画的弧相交于点D ′；（4）过点D '画射线O ′B ′，则∠A ′O ′B ′＝∠AOB ．小聪作法正确的理由是（ ）A ．由SSS 可得△O ′C ′D′≌△OCD ，进而可证∠A ′O ′B ′＝∠AOBB ．由SAS 可得△O ′C ′D ′≌△OCD ，进而可证∠A ′O ′B ′＝∠AOBC ．由ASA 可得△O ′C ′D ′≌△OCD ，进而可证∠A ′O ′B ′＝∠AOBD ．由“等边对等角”可得∠A ′O ′B ′＝∠AOB【变式3-2】（2023春•白银期中）已知∠AOB ，点C 是OB 边上的一点．用尺规作图画出经过点C 与OA 平行的直线．【变式3-3】如图，以△ABC 的顶点A 为圆心，以BC 长为半径作弧，再以顶点C 为圆心，以AB 长为半径作弧，两弧交于点D ；连接AD 、CD ，若∠B ＝56°，则∠ADC 的大小为 度．【例题4】（2023•官渡区一模）如图，点A ，B ，C ，D 在同一直线上，AF ＝DE ，∠A ＝∠D ，AC ＝DB ．求证：△ABF ≌△DCE．【变式4-1】（2023•从化区二模）为了制作燕子风筝，燕子风筝的骨架图如图所示，AB＝AE，AC＝AD，∠BAD＝∠EAC，证明：△ABC≌△AED．【变式4-2】（2023•祥云县模拟）已知：如图，点F、C在线段BE上，AB＝DE，∠B＝∠E，BF＝EC，求证：△ABC≌△DEF．【变式4-3】（2023•乾安县四模）已知：如图，BA＝BD，BE＝BC，∠ABD＝∠CBE，求证：△ABE≌△DBC．【变式4-4】（2023•宁江区二模）如图，△ABC 中，D 是BC 延长线上一点，满足CD ＝AB ，过点C 作CE ∥AB 且CE ＝BC ，连接DE 并延长，分别交AC 、AB 于点F 、G ，求证：△ABC ≌△DCE ．【变式4-5】（2023•五华区校级模拟）如图，已知AB ∥DE ，AB ＝DE ，AF ＝DC ．求证：△ABC ≌△DEF ．【例题5】如图，点D 在AB 上，点E 在AC 上，CD 与BE 相交于点O ，且AD ＝AE ，∠B ＝∠C ，若BE ＝4，则CD ＝　　．【变式5-1】（2022春•成华区期末）如图，在等腰△ABC 中，∠ACB ＝90°，点D 是AC 的中点，过点A 作直线BD 的垂线交BC 的延长线于点E ，若BC ＝4，则CE 的长为 ．【变式5-2】茗茗用同种材料制成的金属框架如图所示，已知∠B ＝∠E ，AB ＝DE ，BF ＝EC ，其中△ABC 的周长为24cm ，CF ＝3cm ，则制成整个金属框架所需这种材料的长度为 cm ．【变式5-3】（2023•青海一模）在△ABC 中，D 是BC 边的中点，若AB ＝9，AC ＝5，则△ABC 的中线AD 长的取值范围是（ ）A ．5＜AD ＜9B ．4＜AD ＜9C ．2＜AD ＜14D ．2＜AD ＜7【例题6】如图，已知OA ＝OB ，OC ＝OD ，∠O ＝50°，∠D＝35°，则∠OBC ＝（ ）A．95°B．120°C．50°D．105°【变式6-1】（2022春•福山区期中）如图，AC是四边形ABCD的对角线，∠1＝∠B，点E、F分别在AB、BC上，BE＝CD，BF＝CA，连接EF．（1）求证：∠D＝∠2；（2）若EF∥AC，∠D＝76°，求∠BAC的度数．【变式6-2】（2023春•青羊区期末）如图在△ABC中，D是BC边上的一点，AB＝DB，BE平分∠ABC，交AC边于点E，连接DE．（1）求证：△ABE≌△DBE；（2）若∠A＝100°，∠C＝40°，求∠DEC的度数．【变式6-3】（2022秋•湟中区校级期末）如图，在△ABC中，D为AB上一点，E为AC中点，连接DE 并延长至点F，使得EF＝ED，连CF．（1）求证：CF∥AB（2）若∠ABC＝50°，连接BE，BE平分∠ABC，AC平分∠BCF，求∠A的度数．【例题7】（2022秋•甘井子区校级月考）如图，点C、E、B、F在同一直线上，AC∥DF，AC＝DF，BF ＝CE，试判断AB和DE的关系，并说明理由．【变式7-1】（2023春•罗湖区校级期末）已知：如图，点A、F、C、D在同一直线上，AF＝DC，AB＝DE，AB∥DE，连接BC，BF，CE．求证：（1）△ABC≌△DEF；（2）BC∥EF．【变式7-2】（2023春•萍乡期末）如图，已知：AB⊥BD，ED⊥BD，AB＝CD，BC＝DE，那么AC与CE 有什么关系？写出你的猜想并说明理由．【变式7-3】如图，在△ABC中，D为AB的中点，F为BC上一点，DF∥AC，延长FD至E，且DE＝DF，联结AE、AF．（1）求证：∠E＝∠C；（2）如果DF平分∠AFB，求证：AC⊥AB．【例题8】如图，AC ＝DC ，BC ＝EC ，请你添加一个适当的条件： ，使得△ABC ≌△DEC ．【变式8-1】如图，已知在△ABC 和△DEF 中，∠B ＝∠E ，BF ＝CE ，点B 、F 、C 、E 在同一条直线上，若使△ABC ≌△DEF ，则还需添加的一个条件是 （只填一个即可）．【变式8-2】如图，AB ＝AE ，AC＝AD，要使△ABC ≌△AED ，应添加一个条件是 ．【变式8-3】问题：如图，在△ABC 和△DEF 中，B ，E ，C ，F 在同一条直线上，AB ＝DE ，若 ．求证：△ABC ≌△DEF ．在①AC ＝DF ，②∠ABC ＝∠DEF ，③BE ＝CF 这三个条件中选择其中两个，补充在上面的问题中，并完成解答．【例题9】（2022春•包头期末）如图，已知点A ，C 在线段BD 两侧，AB ＝AD ，CB ＝CD ，线段AC ，BD 相交A 于点O ．下列结论：①∠ABC ＝∠ADC ；②AC ⊥BD ；③AC 平分∠BAD ；④OB ＝OD ．其中正确的是 　（填写所有正确结论的序号）．【变式9-1】（2023•禅城区校级一模）如图，已知AB＝AC，AD＝AE，∠BAC＝∠DAE，且B、D、E三点共线，（1）证明：△ABD≌△ACE；（2）证明：∠3＝∠1+∠2．【变式9-2】（2022春•沙坪坝区校级期中）如图，点C在线段AB上，AD∥BE，AC＝BE，AD＝BC，CF 平分∠DCE．求证：△DCF≌△ECF【变式9-3】（2023春•浦东新区校级期末）如图，已知AB＝AE，AC＝AD，∠BAD＝∠EAC，AD∥BC．（1）△ADE与△ACB是否全等？说明理由；（2）如果∠B＝30°，∠D＝40°，求∠BAE的度数．【变式9-4】（2022秋•自流井区校级期末）如图，在△ABC和△ADE中，AB＝AD，AC＝AE，∠1＝∠2，AD、BC相交于点F．（1）求证：∠B＝∠D；（2）若AB∥DE，AE＝3，DE＝4，求△ACF的周长．【变式9-5】如图，AD＝CB，E、F是AC上两动点，且有DE＝BF．（1）若点E、F运动至如图（1）所示的位置，且有AF＝CE，求证：△ADE≌△CBF；（2）若点E、F运动至如图（2）所示的位置，仍有AF＝CE，则△ADE≌△CBF还成立吗？为什么？（3）若点E、F不重合，则AD和CB平行吗？请说明理由．。

三角形全等的判定1课题：全等三角形的判定（一）教学目标：1、知识目标：（1）熟记边角边公理的内容；（2）能应用边角边公理证明两个三角形全等.2、能力目标：(1) 通过“边角边”公理的运用，提高学生的逻辑思维能力；(2) 通过观察几何图形，培养学生的识图能力.教学重点：学会运用公理证明两个三角形全等.教学难点：在较复杂的图形中，找出证明两个三角形全等的条件.教学过程：1、公理的发现（1）画图：（投影显示）教师点拨，学生边学边画图.（2）实验让学生把所画的剪下，放在原三角形上，发现什么情况？（两个三角形重合）这里一定要让学生动手操作.（3）公理启发学生发现、总结边角边公理：有两边和它们的夹角对应相等的两个三角形全等（简写成“边角边”或“SAS”）作用：是证明两个三角形全等的依据之一.应用格式：强调：1、格式要求：先指出在哪两个三角形中证全等；再按公理顺序列出三个条件，并用括号把它们括在一起；写出结论.2、在应用时，怎样寻找已知条件：已知条件包含两部分，一是已知中给出的，二时图形中隐含的（如公共边，公共角、对顶角、邻补角、外角、平角等）所以找条件归结成两句话：已知中找，图形中看.3、平面几何中常要证明角相等和线段相等，其证明常用方法：证角相等――对顶角相等；同角（或等角）的余角（或补角）相等；两直线平行，同位角相等，内错角相等；角平分线定义；等式性质；全等三角形的对应角相等地.证线段相等的方法――中点定义；全等三角形的对应边相等；等式性质.2、公理的应用（1）讲解例1.学生分析完成，教师注重完成后的总结.分析：（设问程序）“SAS”的三个条件是什么？已知条件给出了几个？由图形可以得到几个条件？解：（略）（2）讲解例2投影例2：例2如图2，AE＝CF，AD∥BC，AD＝CB，求证：学生思考、分析，适当点拨，找学生代表口述证明思路让学生在练习本上定出证明，一名学生板书.教师强调证明格式：用大括号写出公理的三个条件，最后写出结论. （3）讲解例3（投影）证明：（略）学生分析思路，写出证明过程.（投影展示学生的作业，教师点评）（4）讲解例4（投影）证明：（略）学生口述过程.投影展示证明过程.教师强调证明线段相等的几种常见方法.（5）讲解例5（投影）证明：（略）学生思考、分析、讨论，教师巡视，适当参与讨论.师生共同讨论后，让学生口述证明思路.教师强调解题格式：在“证明”二字的后面，先将所作的辅助线写出，再证明. 3、课堂小结：(1)判定三角形全等的方法：SAS(2)公理应用的书写格式(3)证明线段、角相等常见的方法有哪些？让学生自由表述，其它学生补充，自己将知识系统化，以自己的方式进行建构。

三角形全等的判定（1）主备： 邢通 审核： 课型：新授 总第 课时 时间：一、学习目标1、掌握三角形全等的判定（SSS ）2、初步体会尺规作图3、掌握简单的证明格式二、自学指导认真阅读课本，完成下列要求：1、小组讨论探究1。

（1）满足一个或两个条件的两个三角形是否全等。

（2）满足3个条件时，两个三角形是否全等。

注意分类。

2、小组讨论探究2，交流合作，初步体会尺规作图（具体按第7页画图步骤）3、掌握三角形全等的判定之一（SSS ）4、自主学习例1，初步体会证明的基本过程，并会利用判定（SSS ）进行简单的推理，注意过程格式。

5、利用判定（SSS ）作一个角等于已知角，具体按第8页作法的具体步骤。

6、自学后完成展示的内容，20分钟后，进行展示。

三、展示内容：1、P8，练习2、如图 ，AB ＝AD ，CB ＝CD ，求证：△ABC ≌△ADC3、如图C 是AB 的中点，AD ＝CE ，CD ＝BE ，求证：△ACD ≌△CBE4、如图，AD ＝BC ，AC ＝BD ， 求证：（1）∠DAB ＝∠CBA （2）∠ACD ＝∠BDC_3 _2_ B_ DA DBC （第2题） A F E CD B （第3题） A B C （第4题）54DD5、如图，已知点B 、E 、C 、F 在同一条直线上，AB ＝DE ，AC ＝DF ，BE ＝CF ，求证： （1）△ABC ≌△DEF（2）AB ∥DE四、课后作业1． 如果△ABC 的三边长分别为3，5，7，△DEF 的三边长分别为3，3x －2，2x －1，若这两个三角形全等，则x 等于（ ）A ．73B ．3C ．4D ．5 2．如图，已知AC=DB ，要使△ABC ≌△DCB ，还需知道的一个条件是________．3．已知AC=FD ，BC=ED ，点B ，D ，C ，E 在一条直线上，要利用“SSS”，还需添加条件___________，得△ACB ≌△_______．4．如图△ABC 中，AB=AC ，现想利用证三角形全等证明∠B=∠C ，若证三角形全等所用的公理是SSS 公理，则图中所添加的辅助线应是_____________________．5． 如图，A ，E ，C ，F 在同一条直线上，AB=FD ，BC =DE ，AE=FC ．求证：△ABC ≌△FDE ．6．如图，AB=AC ，BD=CD ，那么∠B 与∠C 是否相等？为什么？D CE B A （第5题） （第6题） AB C D全等三角形的判定（2）主备： 邢通 审核： 课型：新授 总第 课时 时间：一、自学目标：1、会画一个三角形与已知三角形全等（根据两边与夹角对应相等）2、理解并掌握边角边的判定方法3、利用边角边判定方法解决实际问题4、探究具备“SSA ”条件的两个三角形是否全等？二、自学指导认真阅读课本，完成下列要求：1、小组合作学习探究2，注意画图时的规范，用尺规作图注意画法。