江苏省南京市上元中学2015届九年级一轮主题复习学案(专题5_图形与证明)

【基础过关】1.已知｜x ｜=3，｜y ｜=2，且xy ＜0,则x+y 的值为多少？2.若等腰三角形的内角为40º，则其他两个内角为多少度？3.若☉A 与☉B 相切，且☉A 的半径为5cm ，两圆的圆心距为12cm ，则☉B 的半径为多少？【典型例题】例1.已知直角三角形两边x 、y的长满足240x -=，则第三边长为多少？例2.如图2-4-2，正方形ABCD 的边长是2，BE=CE ，MN=1，线段MN 的两端在CD 、AD 上滑动。

当DM 是多少时，△ABE 与以D 、M 、N 为顶点的三角形相似？例3.在直角坐标系中，一次函数2y +的图象与x 轴交于点A ，与y 轴交于点B 。

（1）以原点O 为圆心的圆与直线AB 切于点C ，求切点C 的坐标。

（2）在x 轴上是否存在点P ，使△PAB 为等腰三角形？若存在，请直接写出点P 的坐标；若不存在，请说明理由。

图2-4-2E N MD C B A【课后练习】1．已知等腰△ABC的周长为18㎝，BC=8㎝．若△ABC≌△A´B´C´，则△A ´B´C´中一定有条边等于（）A．7㎝ B．2㎝或7㎝ C．5㎝ D．2㎝或7㎝2．已知⊙O的半径为2，点P是⊙O外一点，OP的长为3，那么以P这圆心，且与⊙O相切的圆的半径一定是（）A．1或5 B．1 C．5 D．1或43．A、B两地相距450千米，甲、乙两车分别从A、B两地同时出发，相向而行．已知甲车速度为120千米/时，乙车速度为80千米/时，以过小时两车相距50千米，则的值是（）A．2或2.5 B．2或10 C．10或12.5 D．2或12.54．已知点Ｐ是半径为２的⊙Ｏ外一点，PA是⊙O的切线，切点为A，且PA=2，在⊙O内作了长为的弦AB，连续PB，则PB的长为。

【基础过关】1．已知一个等腰三角形有两边的长分别为2和5，则它的周长为（ ）A ．7B ．9C ．12D ．9或122．如图，在△ABC 中，点D 、E 分别在AB 、AC 边上，DE//BC ，若AD ：AB =3：4， DE=6，则BC= ________．3．已知△ABC 中，D 、E 分别是两边AB 和AC 的中点，若△ABC 的面积是8cm 2，则四边形BCED 的面积是 cm 2．【典型例题】例1． 如图，△ABC 中，AB ＝AC ，AD 是△ABC 的角平分线，点O 为AB 的中点，连结DO 并延长到点E ，使OE ＝OD ，连结AE ，BE .（1）求证：四边形AEBD 是矩形；（2）当△ABC 满足什么条件时，矩形AEBD 是正方形，并说明理由．例2． 如图1，在△ABC 中，AB=AC ，点D 是BC 的中点，点E 在AD 上． （1）求证：BE=CE ；（2）如图2，若BE 的延长线交AC 于点F ，且BF ⊥AC ，垂足为F ，∠BAC=45°，原题设其它条件不变．求证：△AEF ≌△BCF ．ABC DE【课后作业】1．如图，已知AB ∥CD ，∠C =35°，BC 平分∠ABE ，则∠ABE 的度数是（ ） A ．17.5° B．35° C．70° D ．105°2．如图，在矩形ABCD 中，O 是对角线AC 、BD 的交点，点E 、F 分别是OD 、OC 的中点． 如果AC=10，BC=8，那么EF 的长为（ ）A ．6B ．5C ．4D ．33．如图，在梯形ABCD 中，AB∥CD，∠A=60°，∠B=30°， 若AD=CD=6，则AB 的长等于（ ）．A ．9B ．12C．6D ．185．如图，已知正方形ABCD 的边长为4，对称中心为点P ，点F 为BC 边上一个动点，点E 在AB 边上，且满足条件∠EPF=45°，图中两块阴影部分图形关于直线AC 成轴对称，设它们的面积和为S 1．（1）求证：∠APE=∠CFP ；（2）设四边形CMPF 的面积为S 2，CF=x ，y ＝12s s ． ①求y 关于x 的函数解析式和自变量x 的取值范围，并求出y 的最大值； ②当图中两块阴影部分图形关于点P 成中心对称时，求y 的值．FODCBAE （第1题）（第2题）（第3题）。

【基础过关】1、下列运算正确的是 ( )A ．a 3·a 2＝a 6B ．(x 3)3＝x 6C ．x 5＋x 5＝x 10D ．(－ab )5÷(－ab )2＝－a 3b 32、把x 2y －2y 2x ＋y 3分解因式正确的是( )A ．y (x 2－2xy ＋y 2)B ．x 2y －y 2(2x －y )C ．y (x －y )2D ．y (x ＋y )23、写出一个比－4大的负无理数_______．4、()0106022112cos ---+⎪⎭⎫ ⎝⎛ =______． 5、对于任意不相等的两个实数a ，b ，定义运算※如下：a ※b如3※2=那么8※12＝_______．【典型例题】例1、先化简，再求值：22121124x x x x ++⎛⎫-÷ ⎪+-⎝⎭，其中x ＝t a n 260°－1．例2、《中考指导书》p25 例题4例3、若干块如图长方形、正方形硬纸板，（1）如果要拼一个长为（2a+b ），宽为（a+b ）的矩形，需要A 类卡片_____张，B 类卡片_____张，C 类卡片_____张。

（2）现用A 类卡片3张，B 类卡片1张，C 类卡片2张，拼成一个矩形，请画出矩形；并结合拼图，将a 2+3ab+2b 2分解因式。

例4、计算11111111111111111111234523456234562345⎛⎫⎛⎫⎛⎫⎛⎫----++++------+++ ⎪⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭的结果是 。

A B C【课后作业】1、某市2013年参加中考的考生人数约为85000人，将85000用科学记数法表示为2、如果代数式1x -有意义，那么x 的取值范围是 3、计算10013tan30132π-⎛⎫+--- ⎪⎝⎭（）= ；））（（）（1323213212+---= 4、若x 、y 为实数,03=-+y 3-x 则,)(2013=xy 5、先化简，再求值：()2x 11x 1⎛⎫-÷-⎪+⎝⎭，其中ｘ为方程2x 3x 20++=的根。

备课时间 第 课时 授课时间 姓名【基础过关】1. 如图，在四边形ABCD 中，顺次连接四边中点E ，F ，G ，H ，构成一个新的四边形，请你对四边形ABCD 添加一个条件，使四边形EFGH第1题 第2题 第3题2. 如图，海边立有两座灯塔A 、B ，暗礁分布在经过A 、B 两点的弓形（弓形的弧是⊙O 的一部分）区域内，∠AOB=80°．为了避免触礁，轮船P 与A 、B 的张角∠APB 的最大值为 ．3. 如图，在矩形ABCD 中，AB ＝m （m 是大于0的常数），BC ＝8，E 为线段BC 上的动点（不与B 、C 重合）．连结DE ，作EF ⊥DE ，EF 与射线BA 交于点F ，设CE ＝x ，BF ＝y ．（1）求y 关于x 的函数关系式；（2）若m ＝8，求x 为何值时，y 的值最大，最大值是多少？（3）若12y m，要使△DEF 为等腰三角形，m 的值应为多少？【典型例题】例1：如图①，A 、B 是直线a 上的两个定点，点C 、D 在直线b 上运动（点C 在点D 的左侧），AB ＝CD ＝6cm ．已知a ∥b ，连接AC 、BD 、BC ，把△ABC 沿直线BC 翻折得△A 1BC ．（1）当A 1、D 两点重合时，则AC ＝ cm ．（2）当A 1、D 两点不重合时，连接A 1D ．求证：A 1D ∥BC ．（3）当A 1、D 两点不重合时，若a 、b 间的距离为5cm ，且以点A 1、C 、B 、D 为顶点的四边形是矩形，求AC的长．AB CDE F例2：如图①，在等腰梯形ABCD中，AD∥BC，E是AB的中点，过点E作EF∥BC交CD于点F．AB ＝4，BC＝6，∠B＝60°.（1）求点E到BC的距离.（2）点P为线段EF上的一个动点，过P作PM⊥EF交BC于点M，过M作MN∥AB交折线ADC 于点N，连结PN，设EP＝x.【课后作业】练习第2、4、5题。

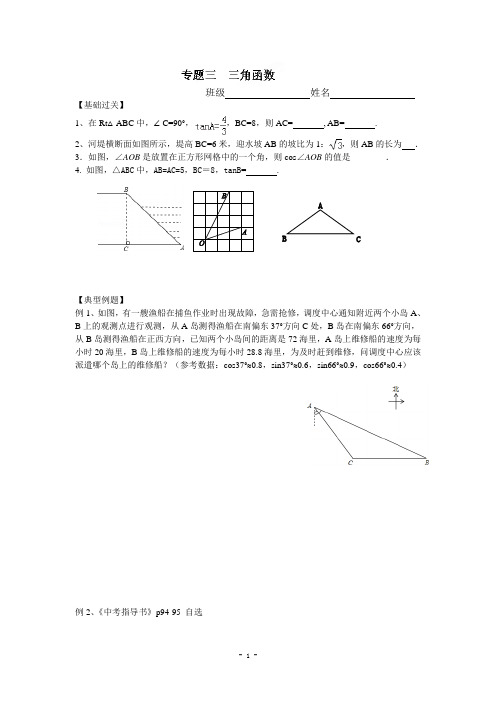
班级 姓名【基础过关】1、在Rt △ABC 中，∠C=90°，，BC=8，则AC= , AB= .2、河堤横断面如图所示，堤高BC=6米，迎水坡AB 的坡比为1：，则AB 的长为 ．3．如图，∠AOB 是放置在正方形网格中的一个角，则cos ∠AOB 的值是________．4. 如图，△ABC 中，AB=AC=5，BC ＝8，tanB = .【典型例题】例1、如图，有一艘渔船在捕鱼作业时出现故障，急需抢修，调度中心通知附近两个小岛A 、B 上的观测点进行观测，从A 岛测得渔船在南偏东37°方向C 处，B 岛在南偏东66°方向，从B 岛测得渔船在正西方向，已知两个小岛间的距离是72海里，A 岛上维修船的速度为每小时20海里，B 岛上维修船的速度为每小时28.8海里，为及时赶到维修，问调度中心应该派遣哪个岛上的维修船？（参考数据：cos37°≈0.8，sin37°≈0.6，sin66°≈0.9，cos66°≈0.4）例2、《中考指导书》p94-95 自选C【课后作业】1.计算：tan60°＋2sin45°－2cos30°的结果是() A．2 B. 3 C. 2 D．12．已知a为锐角，且sin(a－10°)＝32，则a等于()A．50°B．60°C．70°D．80°5．已知：如图，有一块含︒30的直角三角板OAB的直角边长BO的长恰与另一块等腰直角三角板ODC的斜边OC的长相等，把该套三角板放置在平面直角坐标系中，且AB=3.(1)若双曲线的一个分支恰好经过点A，求双曲线的解析式；(2)若把含︒30的直角三角板绕点O按顺时针方向旋转后，斜边OA恰好与x轴重叠，点A 落在点A'，试求图中阴影部分的面积(结果保留π).。

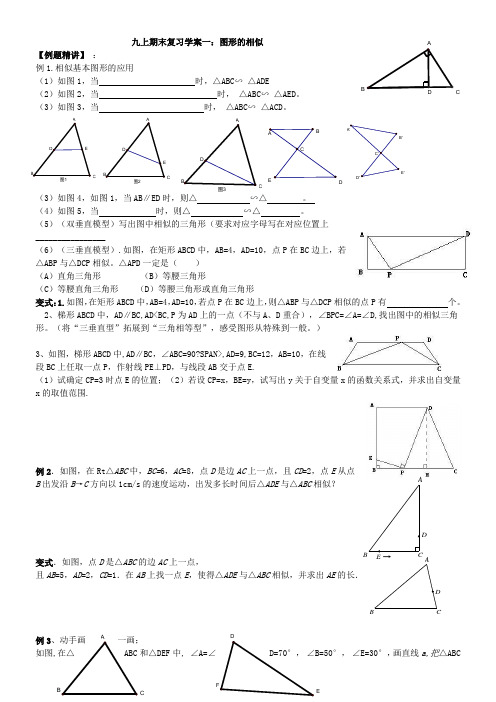
CCCDBCC E九上期末复习学案一：图形的相似【例题精讲】：例1.相似基本图形的应用（1）如图1，当时，△ABC∽△ADE（2）如图2，当时，△ABC∽△AED。

（3）如图3，当时，△ABC∽△ACD。

（3）如图4，如图1，当AB∥ED时，则△∽△。

（4）如图5，当时，则△∽△。

（5）（双垂直模型）写出图中相似的三角形（要求对应字母写在对应位置上________________（6）（三垂直模型）.如图，在矩形ABCD中，AB=4，AD=10，点P在BC边上，若△ABP与△DCP相似。

△APD一定是（）（A）直角三角形（B）等腰三角形（C）等腰直角三角形（D）等腰三角形或直角三角形变式：1.如图，在矩形ABCD中，AB=4，AD=10，若点P在BC边上，则△ABP与△DCP相似的点P有个。

2、梯形ABCD中，AD∥BC,AD<BC,P为AD上的一点（不与A、D重合），∠BPC=∠A=∠D,找出图中的相似三角形。

（将“三垂直型”拓展到“三角相等型”，感受图形从特殊到一般。

）3、如图，梯形ABCD中,AD∥BC，∠ABC=90?SPAN>,AD=9,BC=12，AB=10，在线段BC上任取一点P，作射线PE⊥PD，与线段AB交于点E.（1）试确定CP=3时点E的位置；（2）若设CP=x，BE=y，试写出y关于自变量x的函数关系式，并求出自变量x的取值范围.例2．如图，在Rt△ABC中，BC=6，AC=8，点D是边AC上一点，且CD=2，点E从点B出发沿B→C方向以1cm/s的速度运动，出发多长时间后△ADE与△ABC相似？变式．如图，点D是△ABC的边AC上一点，且AB=5，AD=2，CD=1．在AB上找一点E，使得△ADE与△ABC相似，并求出AE的长．例3如图,和△DEF中, ∠A=∠°，∠E=30°，画直线a,把△ABCC分成两个三角形，画直线b ，把△DEF 分成两个三角形，使△ABC 分成的两个三角形和△DEF 分成的两个三角形分别相似.(要求标注数据)例4. 如图，点D 在△ABC 内，点E 在△ABC 外，∠1＝∠2 ，∠3＝∠4． 求证：△DBE ∽△ABC ．例5：如图，在四边形ABCD 中，AC 、BD 相交于F ，点E 在BD 上，且 判断△ABE 与△ACD 是否相似，并说明理由。

【基础过关】1.南京地区七、八月份天气较为炎热，小华对其中连续十天每天的最高气温进行统计，依次得到以下一组数据：34，35，36，34，36，37，37，36，37，37（单位℃）．则这组数据的众数是 ，中位数是 ．2．甲、乙两人在相同的情况下各打靶107环，则 s 2甲 ．s 2乙(填“＞”、“＜”或“＝”)．3.某校学生在电脑培训前后各参加了一次水平相同的考试，考分都以同一标准划分成“不合格”、“合格”、“优秀”三个等级．为了了解电脑培训的效果，随机抽取其中32名学生两次考试考分等级制成统计图（如图），试回答下列问题：（1）这32名学生经过培训，考分等级“不合格”的百分比由 下降到 ； （2）估计该校640名学生，培训后考分等级为“合格”与“优秀”的学生共有多少名． 【典型例题】例1．小亮与小明做投骰子（质地均匀的正方体）的实验与游戏． （1）在实验中他们共做了50次试验，试验结果如下：① 填空：此次实验中，“1点朝上”的频率是 ；② 小亮说：“根据实验，出现1点朝上的概率最大．”他的说法正确吗？为什么？（2）在游戏时两人约定：每次同时掷两枚骰子，如果两枚骰子的点数之和超过6，则小亮获胜，否则小明获胜．则小亮与小明谁获胜的可能性大？试说明理由例2．在城关中学开展的“我为四川地震灾区献爱心”捐书活动中，校团委为了了解九年级同学的捐书情况，用简单的随机抽样方法从九年级的10个班中抽取50名同学，对这50名同学所捐的书进行分类统计后，绘制了如下统计表：捐书情况统计表（1）在下图中，补全这50名同学捐书情况的频数分布直方图；（2）若九年级共有475名同学，请你估计九年级同学的捐书总册数及学辅类书的册数．朝上的点数 1 2 3 4 5 6 出现的次数1096988不合合优例3、如图,有两个可以自由转动的均匀转盘A、B，转盘A被均匀地分成4等份，每份分别标上1、2、3、4四个数字；转盘B被均匀地分成6等份，每份分别标上1、2、3、4、5、6六个数字．有人为甲、乙两人设计了一个游戏，其规则如下：（1）同时自由转动转盘A、B；（2）转盘停止后，指针各指向一个数字（如指针恰好指在分格线上，那么重转一次，直到指针指向某一数字为止），用所指的两个数字相乘，如果得到的积是偶数，那么甲胜；如果得到的积是奇数，那么乙胜．你认为这样的规则是否公平？请说明理由；如果不公平，请你设计一个公平的规则，并说明理由．【课后作业】1．在一个不透明的盒子中，放入2个白球和1个红球，这些球除颜色外都相同．（1）搅匀后从中任意摸出2个球，请通过列表或树状图求摸出2个球都是白球的概率；（2）搅匀后从中任意摸出1个球，记录下颜色后放回袋中，再次搅匀后从中任意摸出1个球，则2次摸出的球都是白色的概率为；（3）现有一个可以自由转动的转盘，转盘被等分成60个相等的扇形，这些扇形除颜色外完全相同，其中40个扇形涂上白色，20个扇形涂上红色，转动转盘2次，指针2次都指向白色区域的概率为．。

班级姓名【基础过关】1、在Rt△ABC中，∠C=90°，，BC=8，则AC= , AB= .2、河堤横断面如图所示，堤高BC=6米，迎水坡AB的坡比为1：，则AB的长为．3．如图，∠AOB是放置在正方形网格中的一个角，则cos∠AOB的值是________．4.如图，△ABC中，AB=AC=5，BC＝8，tanB= .【典型例题】例1、如图，有一艘渔船在捕鱼作业时出现故障，急需抢修，调度中心通知附近两个小岛A、B上的观测点进行观测，从A岛测得渔船在南偏东37°方向C处，B岛在南偏东66°方向，从B岛测得渔船在正西方向，已知两个小岛间的距离是72海里，A岛上维修船的速度为每小时20海里，B岛上维修船的速度为每小时28.8海里，为及时赶到维修，问调度中心应该派遣哪个岛上的维修船？（参考数据：cos37°≈0.8，sin37°≈0.6，sin66°≈0.9，cos66°≈0.4）例2、《中考指导书》p94-95 自选AC【课后作业】1.计算：tan60°＋2sin45°－2cos30°的结果是 ( )A ．2 B. 3 C. 2 D ．12．已知a 为锐角，且sin(a －10°)＝32，则a 等于 ( ) A ．50° B ．60° C ．70° D ．80°5．已知：如图，有一块含︒30的直角三角板OAB 的直角边长BO 的长恰与另一块等腰直角三角板ODC 的斜边OC 的长相等，把该套三角板放置在平面直角坐标系中，且AB=3.(1)若双曲线的一个分支恰好经过点A ，求双曲线的解析式；(2)若把含︒30的直角三角板绕点O 按顺时针方向旋转后，斜边OA 恰好与x 轴重叠，点A 落在点A '，试求图中阴影部分的面积(结果保留π). AO B C DA’ xy。

苏教版九上数学第一章图形与证明教案1.1等腰三角形的性质和判定(1）新课讲授:1、合作与讨论证明：等腰三角形的两个底角相等.2、思考与讨论怎样证明：等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合。

3、通过上面两个问题的证明，我们得到了等腰三角形的性质定理。

定理:＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿，（简称：＿＿＿＿＿＿）定理：＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿,（简称：＿＿＿＿＿＿)4、你能写出上面两个定理的符号语言吗？（请完成下表）5、思考与探索如何证明“等腰三角形的两个底角相等”的逆命题是正确的？要求：（1)写出它的逆命题：＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿。

（2)画出图形，写出已知、求证，并进行证明.6、通过上面的证明，我们又得到了等腰三角形的判定定理：＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿。

四、新课总结：1、在本节课中,我们用基本事实又证明了哪些定理。

（1）＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿； （2）＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿; （3）＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿。

2、实际上,我们以前曾学习过很多图形的知识，（如：直角三角形全等,平行四边形、矩形、菱形、正方形、梯形等）.对于这些图形，我们通过动手操作也得到了它们的性质和判定，在今后的学习中，我们将进一步证明它们的正确性.1.1等腰三角形的性质和判定（2）一、知识回顾上节课中，我们对等腰三角形的性质定理和判定定理进行了证明，请你写出 等腰三角形性质定理:（1)＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿；（2）＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿。

二、新课讲授1、已知：如图∠EAC 是△ABC 的外角，AD 平分∠EAC ，且AD ∥BC 。

求证：AB ＝AC（1） (2）2、在上图中，如果AB ＝AC ，AD ∥BC ，那么AD 平分∠EAC 吗？如果结论成立,你能证明这个结论吗？三、思考与交流1、证明：（1）等边三角形的每个内角都等于60°。

【基础过关】1．实数a ，ba 的化简结果为________．2．已知直线y 1＝2x －1和y 2＝－x －1的图象如图所示，根据图象填空．(1)当x ______时，y 1＞y 2；当x ______时，y 1＝y 2；当x ______时，y 1＜y 2；(2)方程组21,1y x y x =-⎧⎨=--⎩的解集是____________．3．某村办工厂今年前5个月生产某种产品的总量 c （件）关于时间t （月）的图象如图所示，该厂对这种产品来说（ ）A ．1月至3月每月生产总量逐月增加，4、5两月生产总量逐月减少；B ．1月至3月每月生产总量逐月增加，4、5两月生产总量与3月持平；C 、1月至3月每月生产总量逐月增加，4、5两月均停止生产；D 、1月至 3月每月生产总量不变，4、5两月均停止生产。

4．已知二次函数y 1＝ax 2＋bx ＋c (a ≠0)与一次函数y 2＝kx ＋m (k ≠0)的图象相交于点A (－2,4)，B (8,2)(如图所示)，则能使y 1＞y 2成立的x 的取值范围是____________．5．若直线y =mx +4，x =l ，x =4和x 轴围成的直角梯形的面积是7，则m 的值是（ ）A ．－12B ．－ 23C ．－32D ．－2 6．如图，正三角形ABC 的边长为3 cm ，动点P 从点A 出发，以每秒1 cm 的速度，沿A →B →C 的方向运动，到达点C 时停止．设运动时间为x (单位：秒)，y ＝PC 2，则y 关于x 的函数的图象大致为( )A B C D 7．如图所示，在反比例函数y = k x(k ＞0）的图象上有三点A 、B 、C ，过这三点分别向x 轴、y 轴作垂线，过每一点所作的两条垂线与x 轴，y 轴围成的面积分别为S 1，S 2，S 3，则（ ） A ．S 1＞S 2＞S 3 B ．S 1＜S 2 ＜S 3 C ．S 1＜S 3＜S 2 D ．S 1=S 2 =S 3（第1题）（第2题） （第3题） （第4题）（第6题）【典型例题】例1．某公司推销一种产品，设x(单位：件)是推销产品的数量，y(单位：元)是推销费，如图表示该公司每月付给推销员推销费的两种方案，看图解答下列问题：例2．在直径为AB的半圆内，画出一块三角形区域，使三角形的一边为AB，顶点C在半圆周上，其他两边分别为6和8．现要建造一个内接于△ABC的矩形水池DEFN，其中，DE 在AB上，如图所示的设计方案是使AC=8，BC=6．⑴ 求△ABC中AB边上的高h；⑵ 设DN=x，当x取何值时，水池DEFN的面积最大？⑶ 实际施工时，发现在AB上距B点l．85处有一棵大树．问：这棵大树是否位于最大矩形水池的边上？如果在，为保护大树，请设计出另外的方案，使内接于满足条件的三角形中欲建的最大矩形水池能避开大树．【课后作业】1．不等式组114x x ->⎧⎨≤⎩的解集在数轴上，如图所表示应是（ ）2．如图所示，阴影部分是一个正方形，则此正方形的面积为（ ）A ．8B ．64C ．16D ．323．某人从A 地向B 地打长途电话6分钟，按通话时间收费，3分钟以内收费2．4元，每加 1分钟加收 1元，则表示电话费y （元）与通话时间(分）之间的关系的图像如图所示，正确的是（ ）4．如图所示，在Rt △ABC 中，∠C ＝90○，AB =13，BC =5，则以AC 为直径的半圆的面积为（ ） A ．6π B ．12π C ．36π D ．18π5．a ，b ，c 是三角形的三条边，则关于x 的一次函数222()2y a b c x a b c ab =+-++--的图象不经过第_______限．6．若一次函数(2)y m x m =-+的图象经过第一、二、四象限时，m 的取值范围是_______.7．若点P （1，a ）和Q （－1，,b ）都在抛物线21y x =-+上，则线段PQ 的长是_______。