飞机结构力学第四章

结构力学 第四章习题 参考答案2005级4－1 图示抛物线拱的轴线方程24(fy x l l=−)x ，试求截面K 的内力。

解：（1） 求支座反力801155 kN 16AV AV F F ×=== 0805(5580)0.351500.93625 kN 16BV BV F F ×==−×+×== 0Mc 55880350 kN 4H F f ×−×===（2） 把及代入拱轴方程有:16m l =4m f =(16)16xy =−x （1）由此可得:(8)tan '8x y θ−==（2） 把截面K 的横坐标 ,代入（1），（2）两式可求得: 5m x ==＞, 3.44m y =tan 0.375θ= 由此可得:20.56θ= 则有sin 0.351θ=,cos 0.936θ=最后得出截面k 处的内力为: (上标L 表示截面K 在作用力左边，R 则表示截面在作用力右边)055550 3.44103 kN m K H M M F y =−=×−×=i0cos sin 550.936500.35133.93 kN L sK s H F F F θθ=−=×−×= (5580)0.936500.35140.95 kN R sK F =−×−×==40.95 KN 0sin cos 550.351500.93666.1 kN L NK s H F F F θθ=+=×+×= (5580)0.351500.93638.03 kN R NK F =−×+×=4－2 试求拉杆的半圆三铰拱截面K 的内力。

解：（1）以水平方向为X 轴,竖直方向为Y 轴取直角坐标系，可得K 点的坐标为：2m6mK K x y =⎧⎪⎨==⎪⎩ （2）三铰拱整体分别对A ，B 两点取矩，由平衡方程可解得支座反力：0 20210500 20210500 2100A By B Ay x Ax M F M F F F ⎧=×−××⎪⎪=×+××⎨⎪=−×=⎪⎩∑∑∑=== =＞ 5 kN ()20 kN () 5 kN ()Ay Ax By F F F =−⎧⎪=−⎨⎪=⎩向下向上向左（3）把拱的右半部分隔离，对中间铰取矩，列平衡方程可求得横拉杆轴力为：CN 0 105100MF =×−×∑=＞N 5 kN F =（4）去如图所示的α角，则有：=＞cos 0.6sin 0.8θθ=⎧⎨=⎩于是可得出K 截面的内力，其中：22(6)206525644 kN m 2K M ×=−+×−×−×=isK F (20265)sin 5cos 0.6 kN θθ=−×−×−×=− NK F (20265)cos 5sin 5.8 kN θθ=−−×−×−×=−13K M F r Fr ==（内侧受拉） K 截面作用有力，剪力有突变 且有01sin3032LSK 2F F F F =−=−×=− （2） 22R SK F FF F =−=（3）011sin30(326NKF F F F ==×=拉力）（4）4-4 试求图示三铰拱在均布荷载作用下的合理拱轴线方程。

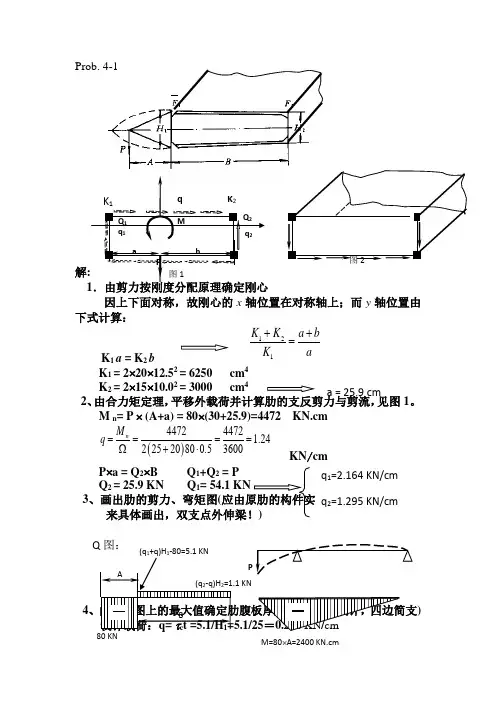
Prob. 4-1解: 1．由剪力按刚度分配原理确定刚心因上下面对称，故刚心的x 轴位置在对称轴上；而y 轴位置由下式计算：K 1 a = K 2 bK 1 = 2⨯20⨯12.52 = 6250 cm 4K 2 = 2⨯15⨯10.02 = 3000 cm 4 2、由合力矩定理，平移外载荷并计算肋的支反剪力与剪流，见图1。

M n = P ⨯ (A+a) = 80⨯(30+25.9)=4472 KN.cmKN /cmP ⨯a = Q 2⨯B Q 1+Q 2 = P Q 2 = 25.9 KN Q 13、画出肋的剪力、弯矩图(应由原肋的构件实际作用力图＋支反力来具体画出，双支点外伸梁！)4、由剪力图上的最大值确定肋腹板厚度(抗剪型板设计，四边简支) 设计载荷：q= τc t =5.1/H 1=5.1/25＝0.204 KN /cm121K K a bK a ++=()44724472 1.2422520800.53600n M q ====Ω+⋅q K 2 K 1 Q 2 Q 1 M q 2q 1 b a 图2 图1Pa = 25.9 cm q 1=2.164 KN/cm q 2=1.295 KN/cmQ 图：80 KN(q 2-q)H 2=1.1 KN M=80⨯A=2400 KN.cmAB公式： ，K=5.6+a /b =B/H 1=80/25=3.24 K= 5.97, E=70000 MPaδ = 3.3.899=3.4 mm5、由弯矩的最大值确定肋上下缘条的面积(上缘条受拉、下缘条受压，且力大小相等、方向相反)：最大弯矩处的缘条内力： N = M max /H 1 = 2400/25=96 KN 上缘条面积由强度计算确定:A * σb = NA *=96000(N)/420 (MPa)=228.57 mm 2，应取 A *＝228.57/0.9=253.97 mm 2 下缘条面积由压杆总体稳定性公式确定：(两端固支，K=4，注失稳的弯曲方向)(正方形) A * =A * == 516.78 mm 2 如按题目给出的受压失稳临界应力值(偏危险)，可得： A * = 96000/280 = 342.86 mm 2 6、前梁腹板的厚度确定：前梁腹板的剪流：q q = q 1+q = 3.404 KN/cm 由公式粗算（不考虑立柱，a 很大）K= 5.6 + = 5.6mm (因厚度合适，可不考虑安装立柱)如考虑立柱，其间距取a = b =250 mm , 则 K=9.38mm7、后梁腹板的厚度确定：后梁腹板的剪流：q h = q 2 - q = 1.295-1.24= 0.055 KN/cmδ=()23.78/a b =22cr K EI P N l π==32**111212I ab A ==*cr A Nσ=δ=()23.78/a b 3.3δ== 2.8δ==＝1 mm可不再考虑立柱设计 。

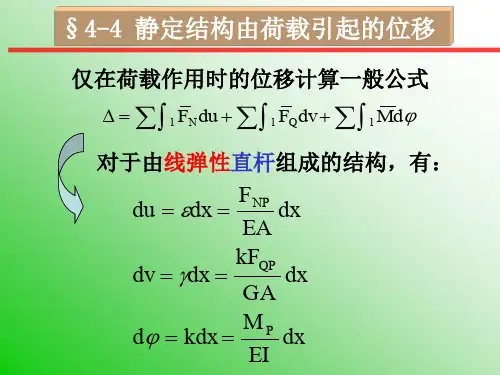
结构力学 第四章习题 参考答案2005级4－1 图示抛物线拱的轴线方程24(fy x l l=−)x ，试求截面K 的内力。

解：（1） 求支座反力801155 kN 16AV AV F F ×=== 0805(5580)0.351500.93625 kN 16BV BV F F ×==−×+×== 0Mc 55880350 kN 4H F f ×−×===（2） 把及代入拱轴方程有:16m l =4m f =(16)16xy =−x （1）由此可得:(8)tan '8x y θ−==（2） 把截面K 的横坐标 ,代入（1），（2）两式可求得: 5m x ==＞, 3.44m y =tan 0.375θ= 由此可得:20.56θ= 则有sin 0.351θ=,cos 0.936θ=最后得出截面k 处的内力为: (上标L 表示截面K 在作用力左边，R 则表示截面在作用力右边)055550 3.44103 kN m K H M M F y =−=×−×=i0cos sin 550.936500.35133.93 kN L sK s H F F F θθ=−=×−×= (5580)0.936500.35140.95 kN R sK F =−×−×==40.95 KN 0sin cos 550.351500.93666.1 kN L NK s H F F F θθ=+=×+×= (5580)0.351500.93638.03 kN R NK F =−×+×=4－2 试求拉杆的半圆三铰拱截面K 的内力。

解：（1）以水平方向为X 轴,竖直方向为Y 轴取直角坐标系，可得K 点的坐标为：2m6mK K x y =⎧⎪⎨==⎪⎩ （2）三铰拱整体分别对A ，B 两点取矩，由平衡方程可解得支座反力：0 20210500 20210500 2100A By B Ay x Ax M F M F F F ⎧=×−××⎪⎪=×+××⎨⎪=−×=⎪⎩∑∑∑=== =＞ 5 kN ()20 kN () 5 kN ()Ay Ax By F F F =−⎧⎪=−⎨⎪=⎩向下向上向左（3）把拱的右半部分隔离，对中间铰取矩，列平衡方程可求得横拉杆轴力为：CN 0 105100MF =×−×∑=＞N 5 kN F =（4）去如图所示的α角，则有：=＞cos 0.6sin 0.8θθ=⎧⎨=⎩于是可得出K 截面的内力，其中：22(6)206525644 kN m 2K M ×=−+×−×−×=isK F (20265)sin 5cos 0.6 kN θθ=−×−×−×=− NK F (20265)cos 5sin 5.8 kN θθ=−−×−×−×=−13K M F r Fr ==（内侧受拉） K 截面作用有力，剪力有突变 且有01sin3032LSK 2F F F F =−=−×=− （2） 22R SK F FF F =−=（3）011sin30(326NKF F F F ==×=拉力）（4）4-4 试求图示三铰拱在均布荷载作用下的合理拱轴线方程。

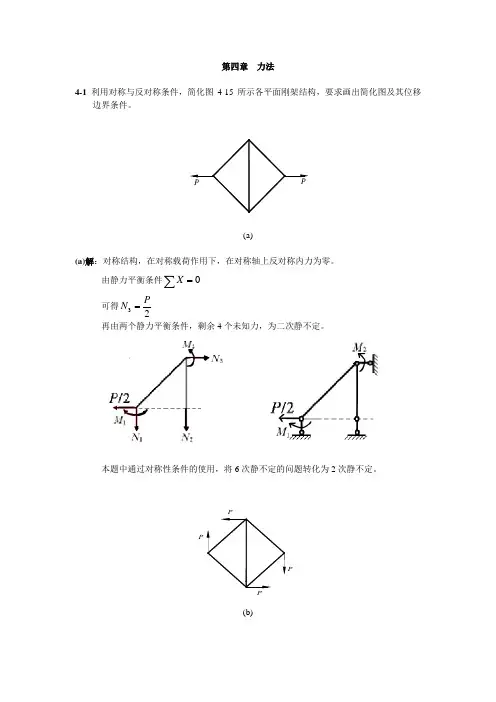
第四章 力法4-1 利用对称与反对称条件，简化图4-15所示各平面刚架结构，要求画出简化图及其位移边界条件。

P P(a)(a)解：对称结构，在对称载荷作用下，在对称轴上反对称内力为零。

由静力平衡条件∑=0X可得23P N =再由两个静力平衡条件，剩余4个未知力，为二次静不定。

本题中通过对称性条件的使用，将6次静不定的问题转化为2次静不定。

1PP(b)(b)解：对称结构，在反对称载荷作用下，在对称轴上对称的内力为零。

受力分析如图所示有2根对称轴，结合平衡方程，剩下三个未知数，为3次静不定。

本题中通过对称性条件的使用，将6次静不定问题转化为3次静不定。

(c)(c)解：对称结构，在对称载荷作用下，在对称轴上反对称内力为零。

有一根对称轴，减少了两个静不定度本题中通过对称性条件的使用，将3次静不定问题转化为1次静不定。

4-2图4-16所示桁架各杆的EA均相同，求桁架各杆的内力。

(a)(a)解：1、分析结构静不定次数。

结构有4个结点8个自由度，6根杆6个约束，3个外部约束。

因此结构静不定次数为1，f=1。

2、取基本状态。

切开2-4杆，取<P>,<1>状态，各杆内力如图。

1234P-P √2P<P>1234P<1>11√22√22√22√22计算影响系数∑=∆EAl N N i p P 11()2422222+=⎪⎪⎭⎫ ⎝⎛⨯+⨯=EA Pa P P EA a ∑=EAl N i1211δ()22222142222+=⎪⎪⎭⎫ ⎝⎛⨯⨯+⨯⨯=EA a EA a 列正则方程：()()02242221=+++P X解之()P X 42321-=3、由11N X N N P +=，得()P X N 423220112-=⎪⎪⎭⎫ ⎝⎛-⋅+= ()P X P N 42212113+=⋅+=()P X N 423220114-=⎪⎪⎭⎫ ⎝⎛-⋅+=()P X N 423220123-=⎪⎪⎭⎫ ⎝⎛-⋅+=()P X N 423210124-=⋅+=()P X P N 42122134+-=⎪⎪⎭⎫ ⎝⎛-⋅+-=4、校核。

飞行器结构力学基础李亚智航空学院·航空结构工程系第4章力法4.1 概述静不定（超静定）结构具有“多余”未知力。

多余未知力（内力或支反力）是由多余约束引起的，也叫做多余约束力。

静不定结构中的多余未知力不能仅由平衡条件求出，而必须引入变形协调条件后才能求解。

力法是计算静不定结构内力和位移的一种基本方法。

力法的基本未知量是力—多余未知力。

4.2 力法原理及力法典型方程力法计算的基本思路：把静不定结构的计算问题转化为静定结构的计算问题，即利用静定结构的计算方法来达到求解静不定结构的目的。

P例1、图示三支点梁A B C一次静不定，有一个多余约束。

B AC P X（2）把多余约束对梁的作用（约束力）用集中力X 表示。

（1）先去掉一个多余约束（譬如可动铰支座B ）。

材料力学的求解方法：去掉多余约束后所得到的静定结构称为力法的基本系统。

本例的基本系统就是一根简支梁。

X 就是多余未知力（多余约束力），只要知道它的大小，就可以应用平衡条件求出原结构系统的支反力和内力（剪力和弯矩）的大小与分布。

A C PB 原系统基本系统A B C PAC X BX∆（3）借助变形几何关系求解多余未知力上式即为力法求解的典型方程（正则方程）。

变形几何关系：0=∆+∆=∆X P B 令为仅在X = 1作用下其作用点的位移，则1δX X ⋅=∆1δ变形几何关系成为：1=⋅+∆X P δA C PB P∆0=∆BP 1P 212例2、二次静不定桁架，共11根杆。

基本系统以两个斜杆1和2的内力作为多余未知力。

解：将两杆切开，等于去掉了两个多余约束，变成静定结构，也就是构成一个基本系统。

12原系统=++P 1P 212原状态P 1P 2载荷状态X 1多余未知力状态1X 2多余未知力状态2外载荷和多余未知力均可看作是作用于基本系统上的外力。

上页图中有以下几层含义：•原结构中多余未知力X1和X2是被动力（由外力引起），而在基本系统中是以主动力（外力）的形式出现的。

静定结构的位移计算习题4—1 (a)用单位荷载法求图示结构B 点的水平位移解：1. 设置虚拟状态选取坐标如图。

2. M P 图和 如图示3. 虚拟状态中各杆弯矩方程为实际状态中各杆弯矩方程为M P =F P x4. 代入公式（4—6）得 △BH =l实际状态1虚拟状态5F P l 15l M P 图图M 图M xM =141012118111EI F EI x F x EI x F x EI dx M M P l l P l P P =⨯⨯+⨯⨯=∑⎰⎰⎰(←)4—1 (b)单位荷载法求图示刚架B 点的水平位移 解：1. 设置虚拟状态选取坐标如图。

2. M P 图和 如图示3. 虚拟状态中各杆弯矩方程为 BD: DC: CA: 实际状态中各杆弯矩方程为 BD: M P =0 DC: M P =40x CA: M P =160+5x 24. 代入公式（4—6）得图M x M =3=M xM-=3△BH =4—2试求图示桁架结点B 的竖向位移，已知桁架各杆的EA =21×104KN 。

1M P 图M 3KN •m340KN •m3KN •m3KN •m)(833.05160)3(40306012401301←=+⨯-+⨯+*=∑⎰⎰⎰⎰cm EI x x x EI x EI x EI dxM M P实际状态虚拟状态解：虚拟状态如图示。

实际状态和虚拟状态所产生的杆件内力均列在表4—1中，根据式4—7可得结点B的竖向位移为表4—1中)(768.010215.16124↓=⨯∙=∆cm KNm KN BV4—3 （a）、（b）试用图乘法求图示结构B 处的转角和C 处的竖向位移。

EI=常数。

M=ql 2M P 图ql 2/81M=1（a ）解：M P 图、单位力偶下作用于B 点的1M 图、单位力下作用于C 点的2M 图EIql ql l ql l EI B 3)21223232221(1222=⨯⨯⨯-⨯⨯⨯=ϕ（ ）（b ）解：M P 图、单位力偶下作用于B 点的1M 图、单位力作用于C 点的2M 图)2183232421(122⨯⨯⨯-⨯⨯⨯=ql l l ql EI B ϕ=ql 3/24EI( ))23242212832232421(1222ql ql l ql ql l ql l ql EI cv ⨯⨯⨯⨯+⨯⨯⨯-⨯⨯⨯⨯=∆)(24)2852232322213221(14222↑-=⨯⨯⨯⨯⨯+⨯⨯⨯-⨯⨯⨯-=∆EI qll ql l ql l l ql l l EI CV= ql4/24EI(↓)（b）ql/2ql2/4l/2（C ）解：M P 图、单位力偶作用于B 点的1M 图、单位力作用于C 点时的2M 图EIl F lF ll EI P P B 12231211322121(12=⨯⨯⨯⨯+⨯⨯⨯⨯-=ϕ( )ll)(12231212232221(12↓=⨯⨯⨯⨯+⨯⨯⨯⨯⨯-=∆EIl F lF l l l F l l EI P P P cv 4—4 （a ）试求图示结构C 点的竖向位移。