下载文档原格式
飞行器结构力学基础电子教学教案第一章：飞行器结构力学概述1.1 教学目标让学生了解飞行器结构力学的定义和研究对象。
让学生理解飞行器结构力学在航空航天工程中的重要性。
让学生掌握飞行器结构力学的基本概念和原理。
1.2 教学内容飞行器结构力学的定义和研究对象。
飞行器结构力学的重要性。
飞行器结构力学的基本概念和原理。
1.3 教学方法采用讲解和案例分析相结合的方式进行教学。
通过多媒体演示和动画视频帮助学生形象理解飞行器结构力学的基本概念和原理。
1.4 教学评估进行课堂讨论和提问，检查学生对飞行器结构力学的基本概念和原理的理解程度。
布置课后作业，要求学生运用所学的知识分析和解决实际问题。
第二章：飞行器结构元件2.1 教学目标让学生了解飞行器结构元件的分类和特点。
让学生掌握梁、板、壳等基本结构元件的受力分析和设计方法。
2.2 教学内容飞行器结构元件的分类和特点。
梁的受力分析和设计方法。
板的受力分析和设计方法。
壳的受力分析和设计方法。
2.3 教学方法采用讲解和案例分析相结合的方式进行教学。
通过多媒体演示和动画视频帮助学生形象理解飞行器结构元件的受力分析和设计方法。
2.4 教学评估进行课堂讨论和提问，检查学生对飞行器结构元件的受力分析和设计方法的理解程度。
布置课后作业，要求学生运用所学的知识分析和解决实际问题。
第三章：飞行器结构力学分析方法3.1 教学目标让学生了解飞行器结构力学分析方法的分类和特点。
让学生掌握静态分析和动态分析的方法和应用。
3.2 教学内容飞行器结构力学分析方法的分类和特点。
静态分析的方法和应用。
动态分析的方法和应用。
3.3 教学方法采用讲解和案例分析相结合的方式进行教学。
通过多媒体演示和动画视频帮助学生形象理解飞行器结构力学分析方法的特点和应用。
3.4 教学评估进行课堂讨论和提问，检查学生对飞行器结构力学分析方法的特点和应用的理解程度。
布置课后作业，要求学生运用所学的知识分析和解决实际问题。
第四章：飞行器结构强度和稳定性分析4.1 教学目标让学生了解飞行器结构强度和稳定性分析的定义和目的。
第二章 静定结构的内力计算一、平面杆系结构2-1、（例题）已知：平面桁架结构的形状尺寸及受载情况如图1-11所示。
试求结构内力。
解：（1）分析结构组成：结构可以看成是以三角形桁架567为基本系统，分别用两根不在同一直线上的双铰杆逐次连接4、3、2、1节点组成的简单桁架。
结构本身是静定的。
现将结构用一平面铰5和一双铰杆3与基础相连，约束正好够，双铰杆不通过平面铰5，分布合理。
（2）根据判断零力杆的原则，可知1-2、1-6、2-3、2-7、5-6、6-7杆轴力均为零。
（3）用节点法求其余各杆内力。
取节点4为分离体得：∑=0XN 34=N 45∑=0Y P N=47取节点7为分离体得： ∑=0X 3757N N =∑=0Y02222475737=++N N N ∴P N N 225737-== 取节点3为分离体得：∑=0X 0223437=+N N∑=0Y33722R N = ∴234PN =23P R -= （R 3为负值，表示3点支反力R 3方向与所设方向相反。
）（4）将求得的各杆轴力标在图上或列于表中。
2-2、判断图2-4中所示个桁架结构的静定性，并指出零力杆。
解：(1)结构静定。
杆1-2、1-3、2-3、3-5、6-4、6-5、2-4是零力杆。
(2)结构静定。
杆1-2、1-4是零力杆。
(3)结构静定。
杆2-3、3-4、1-4是零力杆。
(4)结构静定。
杆2-4、3-4是零力杆。
2-3、平面桁架的几何尺寸和载荷情况如图2-5中所示，用节点法计算桁架结构各杆的内力。
解：（1）0,2,0,,0,,0,06857564536252312=-====-===N P N N P N N P N N N （2）（3）N N P N N P N N P N N P N P N 3,0,2,0,3,0,2,0,3,257474645352524231312-====-====-==P N N 3,05747-==（4）P N N P N N P N N P N 22,0,22,0,,0,2245352523241412==-====-= （5）P N P N P N P N P N -=====3989384734,22,22,22,22，其余为零力杆。
【大学课件】飞机结构力学电子教学教案第一章：课程介绍与基本概念1.1 课程背景与意义介绍飞机结构力学的发展历程及其在航空航天领域的重要性。
强调本课程的目标和意义，即培养学生对飞机结构力学的理解和应用能力。
1.2 课程内容概述概述课程的主要内容，包括飞机结构的基本类型、受力分析、材料力学性质等。
1.3 教学方法与要求介绍本课程的教学方法，包括课堂讲解、案例分析、实验实践等。
对学生的学习要求进行说明，包括课堂参与、作业完成、期末考试等。
第二章：飞机结构的基本类型与特点2.1 飞机结构的基本类型介绍飞机结构的主要类型，包括梁、板、壳、框架等。
2.2 飞机结构的特点分析飞机结构的特点，包括轻质、高强、耐腐蚀、可制造性等。
2.3 实际案例分析通过实际案例分析，让学生更好地理解飞机结构的基本类型和特点。
第三章：飞机结构的受力分析3.1 飞机结构的受力类型介绍飞机结构所受的各种力，包括重力、气动力、惯性力等。
3.2 飞机结构的受力分析方法介绍飞机结构的受力分析方法，包括静态分析、动态分析等。
通过实际案例分析，让学生更好地理解飞机结构的受力分析方法和过程。
第四章：飞机结构的材料力学性质4.1 材料的应力与应变介绍材料的应力与应变概念，包括应力应变关系、弹性模量等。
4.2 材料的屈服与破坏分析材料的屈服条件、破坏形式及其影响因素。
4.3 材料的选用与匹配介绍飞机结构材料的选择原则，包括强度、刚度、耐腐蚀性等。
第五章：飞机结构的设计与优化5.1 飞机结构设计的基本原则介绍飞机结构设计的基本原则，包括安全性、可靠性、经济性等。
5.2 飞机结构设计的步骤与方法详细介绍飞机结构设计的步骤与方法，包括需求分析、方案设计、详细设计等。
5.3 飞机结构的优化方法介绍飞机结构的优化方法，包括拓扑优化、尺寸优化等。
第六章：飞机结构的连接与接头设计6.1 飞机结构连接的类型介绍飞机结构连接的类型，包括螺栓连接、焊接连接、粘接连接等。
第二章 薄板的弯曲（习题解答）2-1 写出2-1图所示矩形薄板的边界条件。
OA 为简支边，并作用有分布的弯矩M 。
BC 边为固支边，OC 边为简支边。
AB 边为自由边。
解：OA 边：M x w D y w u x w D M w x x x x x -=∂∂-=∂∂+∂∂-======0220222200)(0；OC 边：0)(00220222200=∂∂-=∂∂+∂∂-======y y y y y y wD x w u y w D M w ；BC 边：00=∂∂===ax a x xww ；AB 边：0)(2222=∂∂+∂∂-===b y by yx wu y w D M0])2([)(2333=∂∂∂-+∂∂-=∂∂+==by by yx y y x w u y w D xM Q2-2 如图2-2所示，矩形薄板OA 边和OC 边为简支边，AB 和BC 为自由边，在点B 受向下的横向集中力P 。
试证w mxy =可作为该薄板的解答，并确定常数m 、内力及边界处反力。
解：mxy w =满足平衡微分方程0/4==∇D q wOC 边上：0)(0022220＝；==∂∂+∂∂-=y y x wu y w D wOA 边上：0)(0022220＝；==∂∂+∂∂-=x x y wu x w D wAB 边上：0])2([0)(23332222=∂∂∂-+∂∂-=∂∂+∂∂-==by b y y x wu y w D x w u y w D ；BC 边上：0])2([0)(23332222=∂∂∂-+∂∂-=∂∂+∂∂-==ax a x y x wu x w D y w u x w D ；在B 点上：P m u D y x wu D by a x -=--=∂∂∂--==)1(2)()1(2,2)1(2u D Pm -=⇒所以)1(2u D Pxyw -=0)(2222=∂∂+∂∂-=y wu x w D M x ；0)(2222=∂∂+∂∂-=x w u y w D M y ；2)1(2P y x w u D M xy-=∂∂∂--= ；02=∇∂∂-=w xD Q x ；02=∇∂∂-=w y D Q y P R R P y x wu D R O C AA ==-=∂∂∂--=；)()1(222-3 如图2-3所示，半椭圆形薄板，直线边界为简支边，曲线边界ACB 为固支边，承受横向载荷0q=q xa 。
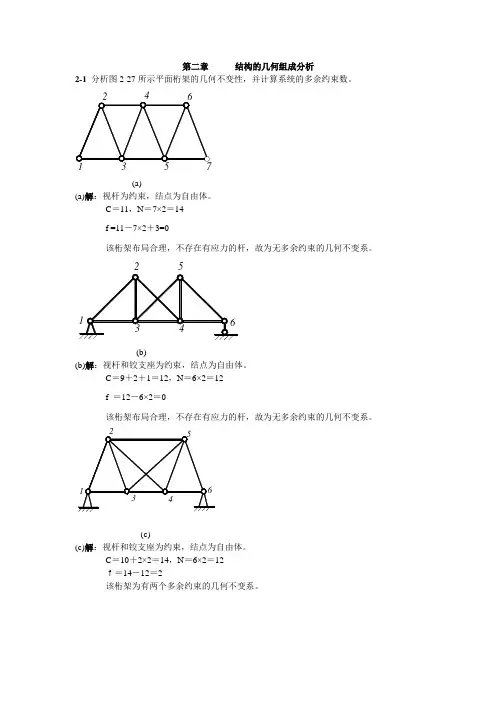
第二章 结构的几何组成分析2-1 分析图2-27所示平面桁架的几何不变性，并计算系统的多余约束数。
3571(a)(a)解：视杆为约束，结点为自由体。
C ＝11，N ＝7×2＝14f =11－7×2＋3=0该桁架布局合理，不存在有应力的杆，故为无多余约束的几何不变系。
(b)(b)解：视杆和铰支座为约束，结点为自由体。
C ＝9＋2＋1＝12，N ＝6×2＝12f ＝12－6×2＝0该桁架布局合理，不存在有应力的杆，故为无多余约束的几何不变系。
(c)(c)解：视杆和铰支座为约束，结点为自由体。
C ＝10＋2×2＝14，N ＝6×2＝12ｆ＝14－12＝2该桁架为有两个多余约束的几何不变系。
1217(d)(d)解：视杆和铰支座为约束，结点为自由体。
C ＝30＋3＝33，N ＝17×2＝34ｆ＝33－34＝-1故该桁架为几何可变系。
8(e)(e)解：视杆为约束，结点为自由体。
C ＝13，N ＝8×2＝16ｆ＝13－16＋3＝0将1-2-3-4、5-6-7-8看作两刚片，杆3-6、杆2-7、杆4-5相互平行，由两刚片原则知，为瞬时可变系统。
6(f)(f)解：视杆和固定铰支座为约束，结点为自由体。
C ＝22＋3×2＝28，N ＝14×2＝28ｆ＝28－28＝0将12-13-14、7-11-12、1-2-3-4-5-6-7-8-9-10看作三刚片，三刚片由铰7、铰12、铰14连结，三铰共线，故该桁架为瞬时可变系统。
(g)(g)解：视杆和固定铰支座为约束，结点为自由体。
C＝24＋4×2＝32，N＝16×2＝32ｆ＝32－32＝0由于杆15-14-3、杆12-11-4、杆9-5相交于一点，故该桁架为瞬时可变系。
(h)(h)解：视杆和固定铰支座为约束，结点为自由体。
C＝12＋2×2＝16，N＝8×2＝16ｆ＝16－16＝0该桁架布局合理，加减二元体之后，无有应力的杆，故该桁架为无多余约束的几何不变系。
