当前位置：文档之家 › 飞行器结构力学课后习题答案第2章

飞行器结构力学课后习题答案第2章

  • 格式：pdf
  • 大小：1.05 MB
  • 文档页数：10

下载文档原格式

  / 10

合集下载

飞行器结构力学课后答案

飞行器结构力学课后答案

F2 1 P 3
3-3 平面刚架的形状、尺寸及受载情况如图所示，求刚架的弯矩和图（ｄ）的扭矩，并作出弯 矩（扭矩）图。
8
l
1 2
4 P
3
(a) (a)解：该结构为无多余约束的几何不变结构。
Px1 0 x1 l M Pl 0 x 2 l P(l x )0 x l 3 3
1
2 4 6 7 5
3 8
(f) (f)解：分别视阴影区为三个刚片。由二刚片规则，铰 2、铰 4、铰 5 与右侧刚片组成一刚片， 再由二刚片规则该刚片与左侧刚片组成一刚片， 可知为无多余约束的几何不变系， 再与下侧 刚片组成刚片，可知该系统为无多余约束的几何不变系。
1
3
2 4
(g) (g)解：该结构为 1 次封闭刚架，外部有一多余约束。 ｆ＝3＋1＝4 该结构为有 4 个多余约束的几何不变系统。
N 24 2Q
N 21 N 24 2
杆件 内力 1-2
N 21 Q
2-3 0 2-4 3-4 0
Q
2Q
3
a
45°
45°
4
Q
2 1
(f)
6
(f)解： （1） f 5 3 4 2 0 故该结构为无多余约束的几何不变结构。 （2）零力杆：杆 2-3，杆 3-4，杆 1-2。
N13 3P
3
N12 3
2
N13 0
对于结点 3：
N3-4
N3-1
N 34 N 31 3P
4
对于结点 4：
N4-6
N4-3
N 46 N 43 3P
2
对于结点 2：

结构力学章节习题及参考答案

结构力学章节习题及参考答案
第3章静定梁与静定刚架习题解答
习题3.1是非判断题
(1) 在使用内力图特征绘制某受弯杆段的弯矩图时，必须先求出该杆段两端的端弯矩。（ ）
(2) 区段叠加法仅适用于弯矩图的绘制，不适用于剪力图的绘制。（ ）
(3) 多跨静定梁在附属部分受竖向荷载作用时，必会引起基本部分的内力。（ ）
(4)习题3.1(4)图所示多跨静定梁中，CDE和EF部分均为附属部分。（ ）
(7) 习题2.1(6)(a)图所示体系去掉二元体EDF后，成为习题2.1(6) (c)图，故原体系是几何可变体系。( )
习题 2.1(6)图
习题2.2填空
(1) 习题2.2(1)图所示体系为_________体系。
习题2.2(1)图
(2) 习题2.2(2)图所示体系为__________体系。
习题 2-2(2)图
（4）习题5.1(3)图(a)和(b)所示两结构的变形相同。（ ）
习题7.2填空题
（1）习题5.2(1)图(a)所示超静定梁的支座A发生转角，若选图(b)所示力法基本结构，则力法方程为_____________，代表的位移条件是______________，其中1c=_________；若选图(c)所示力法基本结构时，力法方程为____________，代表的位移条件是______________，其中1c=_________。
(3) 习题7.2(3)图所示刚架各杆的线刚度为i，欲使结点B产生顺时针的单位转角，应在结点B施加的力矩MB=______。
习题 7.2(1)图习题 7.2(2)图 习题 7.2(3)图
(4) 用力矩分配法计算习题7.2(4)图所示结构（EI=常数）时，传递系数CBA=________，CBC=________。

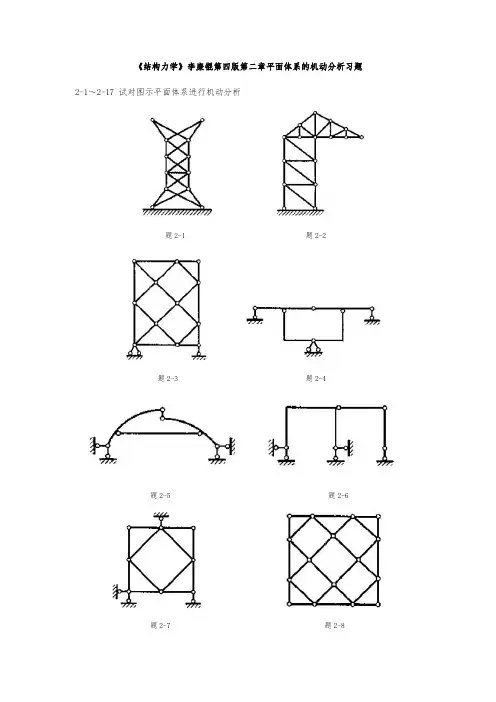
李廉锟第四版《结构力学》第2章平面体系的机动分析习题+参考答案

李廉锟第四版《结构力学》第2章平面体系的机动分析习题+参考答案

《结构力学》李廉锟第四版第二章平面体系的机动分析习题2-1～2-17试对图示平面体系进行机动分析题2-1题2-2题2-3题2-4题2-5题2-6题2-7题2-8题2-9（a、b处非结点）题2-10（k处非结点）题2-11题2-12题2-13题2-14题2-15（k处非结点）题2-16题2-172-18、2-19添加最少数目的链杆和支承链杆，使体系成为几何不变，而且无多余约束。

题2-18题2-19《结构力学》李廉锟第四版第二章平面体系的机动分析参考答案题2-1说明：自上往下依次拆除二元体，或者自下往上依次添加二元体，故体系为有一个多余约束的几何不变体系（多余约束：中间的横杆或者也可以看成支座上多了一根水平杆）。

题2-2说明：如图所示取刚片1和刚片2，采用二刚片规则（两刚片用一个铰和一根不通过此铰的链杆相联），为几何不变体系，而且没有多余联系。

刚片1由二元体组成，刚片2从大地向上组装二元体组成。

题2-3说明：先不考虑支座的三根链杆，考虑上部几何构造，去掉二元体简化分析，取如上图所示刚片1、刚片2和刚片3。

刚片1和刚片2通过一个实铰联结；刚片1和刚片3通过两根平行链杆联结，交于无穷远处；刚片2和刚片3通过两根平行链杆联结，交于无穷远处；三铰不共线，故上部无多余约束且几何不变。

最后上部与大地通过一个铰和一根不通过此铰的链杆相联，故整个体系为无多余约束的几何不变体系。

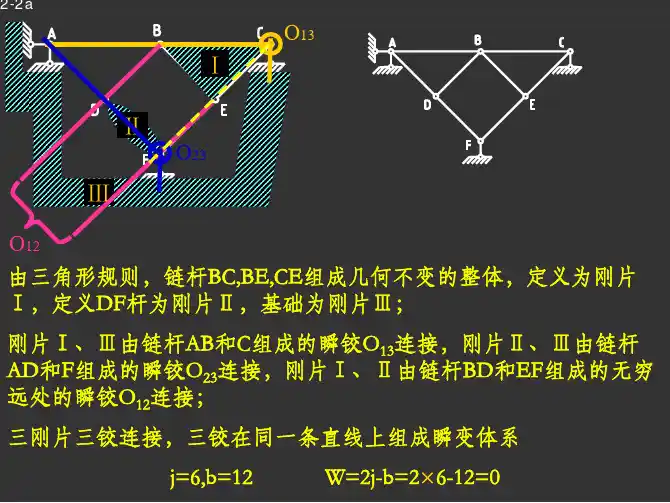
题2-4说明：如上图所示取刚片1、刚片2和刚片3，刚片1和刚片2交于铰12O ，刚片1和刚片3交于铰13O ，刚片2和刚片3交于铰23O ，三铰不共线，故原体系为无多余约束的几何不变体系。

题2-5说明：将大地等效成一根链杆，取如图所示刚片1和刚片2，显然两刚片通过三根链杆相联，且三根链杆既不相互平行也不相交于一点，故原体系为无多余约束的几何不变体系。

题2-6说明：先拆除二元体以简化分析，可知右部分为常变部分；左部分为有一个多余约束的几何不变体系，故体系为几何常变体系。

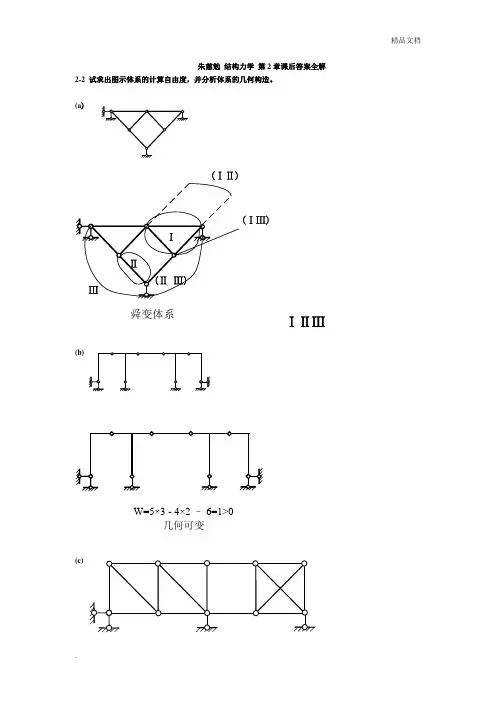
结构力学课后习题答案

结构力学课后习题答案

朱慈勉 结构力学 第2章课后答案全解2-2 试求出图示体系的计算自由度，并分析体系的几何构造。

(a)ⅠⅡⅢ(ⅠⅡ)(ⅠⅢ)(Ⅱ Ⅲ)舜变体系`ⅠⅡⅢ(b)W=5×3 - 4×2 – 6=1>0几何可变(c)有一个多余约束的几何不变体系(d)2-3 试分析图示体系的几何构造。

(a)(ⅠⅢ)ⅠⅡⅢ(ⅠⅡ)(Ⅱ Ⅲ)几何不变W=3×3 - 2×2 – 4=1>0可变体系ⅠⅡⅢ（ⅠⅡ）（ⅠⅢ）（ⅡⅢ）几何不变2-4 试分析图示体系的几何构造。

(a)（ⅠⅢ）（ⅠⅡ）（ⅡⅢ）ⅠⅡⅢ几何不变(b)W=4×3 -3×2 -5=1>0几何可变体系ⅢⅠⅡ（ⅠⅢ）（ⅡⅢ）（ⅠⅡ）几何不变(d)（ⅠⅡ）ⅢⅠⅡ（ⅡⅢ）（ⅠⅢ）二元杆有一个多余约束的几何不变体ⅠⅡⅢ（ⅠⅢ）（ⅡⅢ）（ⅠⅡ）舜变体系(f)ⅠⅡⅢ（ⅠⅢ）（ⅡⅢ）（ⅠⅡ）无多余约束内部几何不变ⅠⅡⅢ（ⅠⅢ）（ⅠⅡ）（ⅡⅢ）二元体(h)ⅠⅡⅢ（ⅠⅢ）（ⅠⅡ）（ⅡⅢ）二元体多余约束W=3×8 - 9×2 – 7= -1, 有1个多余约束2-5 试从两种不同的角度分析图示体系的几何构造。

(a)（ⅠⅢ）ⅠⅡⅢ（ⅠⅡ）（ⅡⅢ）舜变体系(b)ⅠⅡⅢ（ⅠⅡ）（ⅡⅢ）（ⅠⅢ）几何不变同济大学朱慈勉 结构力学 第3章习题答案3-2 试作图示多跨静定梁的弯矩图和剪力图。

(a)4P F a2P F a 2P F a Ｍ4P F Ｑ34P F 2P F(b)ABCaa aaaF P a DEFF P2m6m2m4m2mABCD10kN2kN/m４2020M Q10/326/3４10(c)21018018040M1560704040Q(d)3m2m2mA B CEF15kN 3m3m4m20kN/mD 3m2m2m2mA2m 2m2mABCD E FG H 6kN ·m4kN ·m 4kN2m7.5514482.524MQ3-3 试作图示刚架的内力图。

飞机结构力学_第2章

飞机结构力学_第2章

2.4.1 虚功原理


力学中最基本而且最普遍的原理之一。 用途：

求解平衡问题最一般的方法。 处在平衡状态中的任何系统，包括刚体、弹性体以及 塑性体。

适用范围：

2.4.1 虚功原理

虚位移与虚功

实位移（u）

由外力引起的、与外力紧密相关的、客观存在着的位移。

实功（W）

外力在相应实位移上所做的功、弹性体内力在相应变形上所做 的功。

扭转应变能
MT r J

dU T
f
2 2 1 1 M T dL 2 1 M T dL dfdL fr df 2 GJ 2 2 GJ
2 1 M T dL UT 2 L GJ
2.2.2 几种基本变形的应变能

组合变形下的应变能



在外载荷作用下，刚架结构杆件的内力有轴力、剪力 、弯矩和扭矩（对空间刚架），杆件产生的变形有拉 压、转角、杆截面在水平方向、垂直方向剪切变形， 和绕中心扭转产生的剪切变形。 当杆件变形很微小时，每一种内力仅在和自己相应的 变形上做功。 整个结构的应变能：
h1
q
1
L
h2
常 用 元 件 的 广 义 力 和 广 义 位 移
第2章
能量原理及其在结构分析中的应用



2.1 2.2 2.3 2.4 2.5 2.6 2.7
弹性力学问题及基本方程 功和能的概念 广义力与广义位移 虚功原理和最小位能原理 余虚功原理和最小余能原理 叠加原理与位移互等定理 能量原理在结构分析中的应用
假想的、满足约束条件的、任意的、微小的连续位移。 对于弹性体，凡是在内部满足变形连续条件、在边界上满足几 何约束条件的任何一种微小位移都可选作为虚位移。 在发生虚位移的瞬间，弹性系统原外力和内力均保持不变。

结构力学第2章习题及参考答案

结构力学第2章习题及参考答案

8 kN 20 kN
HI
J ⅠK
L
2 1
AC
D
E ⅠF
G
B
2.5m6 15m
2.5 m
（a）
K
LD
FNJK D
FN2
FNEF FD
G
B
FBy （b
）
解：（1）判断零杆。如图（a）所示。
（2）求支座反力
F x 0 ， FAx 0
M A 0 ， FB y 12.67 kN
F y 0 ， FA y 15.33 kN
5 29
MK
M
0 K
FH yK
510 130 3 120
kN
m
FQK FQ0K cosK FH sinK 52
5 130 29
2 0 29
FNK FN0K sinK FH cosK 52
2 130 29
5 140 kN 29
2-12 图示圆弧三饺拱，求支座反力及截面 D 的 M 、FQ 、FN 值。 20kN/m
D
C
5m
5m
FH
30
A 5m
B 5m
FH
FAy
FBy
习题 2-12 图
解 （1）求支座反力。
FB y 100 kN ， FA y 100 kN ， FH 50 kN
（2）求等代梁 D 截面内力
M
0 D
FAy
2.5
1 2
20 2.52
187.5kNm
FQ0D FAy 20 2.5 50 kN
30 kN A 4 B 30 kN
3×2m
N 1
N
D
N
CN 2 E
N3

飞行力学部分作业答案(1)



+
Lga
−D
C

−L
+
0 0 mg

cosθ cosψ
Lgb
=

cosθ
sinψ
− sinθ
sinθ sinφ cosψ − cosφ sinψ sinθ sinφ sinψ + cosφ cosψ
sinφ cosθ
sinθ cosφ cosψ + sinφ sinψ
补充：试解释飞行包线的形状？ 最大平飞速度：
Vmax =
2Ta CD ρ S
Ta 、 ρ 、 CD 都随高度变化
航空飞行器飞行动力学
对于跨音速飞机：可用推力随高度的增加而降低，其主导作用，这样组合参
数
Ta CD ρ
随高度的增加而降低，因而Vmax
随高度的增加一直减小；
对于超音速飞机：通常在对流层内Vmax 随高度的增加而增大，在平流层中则 随高度的增加而减小。原因：对流层中，音速降低，使同一速度所对应的 M
Ta
=
D
=
CD
1 2
ρV
2S
= 13133N
航空飞行器飞行动力学
补充：跃升时间的计算：
dH = V sin γ dt
dt
=
V
dH sin
γ
∫ 积分： ∆t = H1 dH 通过数值积分求
H0 V sin γ
sin θ
cosφ
sinψ
− sinφ
cosψ

cosφ cosθ

Lga
=
ccoossθθaa
cosψ a sinψ a
− sinθa

结构力学课后习题答案

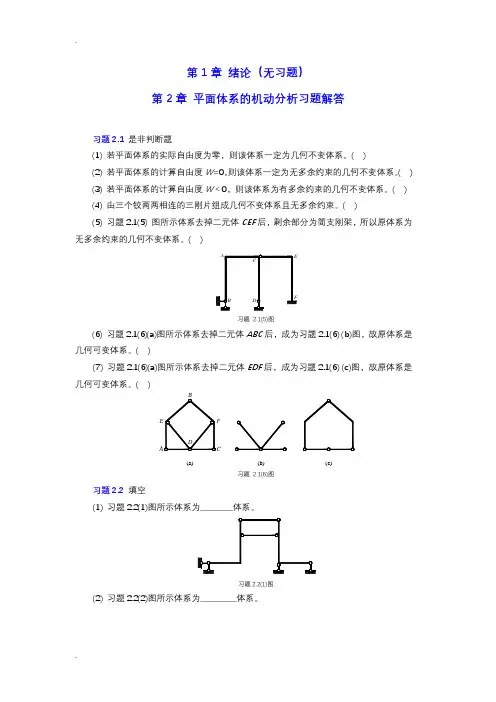
习题及参考答案【习题2】【习题3】【习题4】【习题5】【习题6】【习题8】【习题9】【习题10】【习题11】【习题12】【习题13】【习题14】【参考答案】习题22-1～2-14试对图示体系进行几何组成分析，如果是具有多余联系的几何不变体系，则应指出多余联系的数目。

题2-1图题2-2图题2-3图题2-4图题2-5图题2-6图题2-7图题2-8图题2-9图题2-10图题2-11图题2-12图 题2-13图 题2-14图习题33-1 试作图示多跨静定梁的M 及Q 图。

(b)(a)20kN40kN20kN/m40kN题3-1图3-2 试不计算反力而绘出梁的M 图。

(b)5kN/m40kN(a)题3-2图习题44-1 作图示刚架的M 、Q 、N 图。

(c)(b)(a)20kN /m2kN /m题4-1图4-2 作图示刚架的M 图。

P(e)(d)(a)(b)(c)20k N /m4kN题4-2图4-3 作图示三铰刚架的M 图。

(b)(a)题4-3图4-4 作图示刚架的M 图。

(a)题4-4图4-5 已知结构的M 图，试绘出荷载。

(b)(a)题4-5图4-6 检查下列刚架的M 图，并予以改正。

(e)(g)(h)P(d)(c)(a)(b)(f)题4-6图习题55-1 图示抛物线三铰拱轴线方程x x l lfy )(42-=，试求D 截面的内力。

题5-1图5-2 带拉杆拱，拱轴线方程x x l lfy )(42-=，求截面K 的弯矩。

C题5-2图 题5-3图5-3 试求图示带拉杆的半圆三铰拱截面K 的内力。

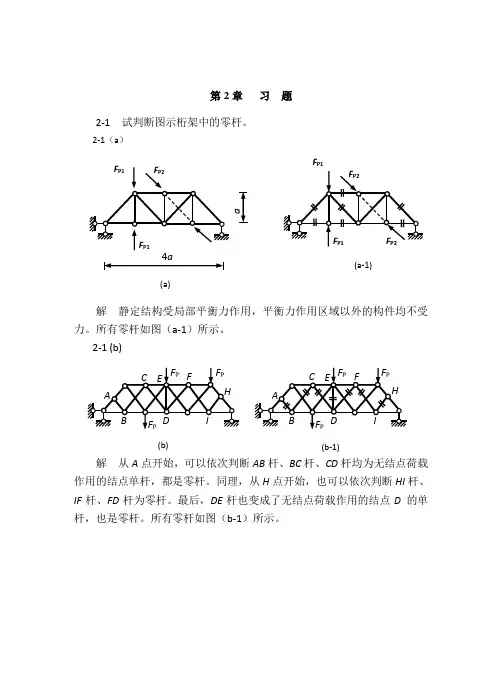
习题66-1 判定图示桁架中的零杆。

(c)(b)题6-1图6-2 用结点法计算图示桁架中各杆内力。

(b)题6-2 图6-3 用截面法计算图示桁架中指定各杆的内力。

(b)题6-3图6-4 试求图示组合结构中各链杆的轴力并作受弯杆件的M 、Q 图。

(a)题6-4图6-5 用适宜方法求桁架中指定杆内力。

(c)(b)(a)题6-6图习题88-1 试作图示悬臂梁的反力V B 、M B 及内力Q C 、M C 的影响线。

南京航空航天大学 结构力学 课后习题答案 第2章

第二章 薄板的弯曲（习题解答）2-1 写出2-1图所示矩形薄板的边界条件。

OA 为简支边，并作用有分布的弯矩M 。

BC 边为固支边，OC 边为简支边。

AB 边为自由边。

解：OA 边：M x w D y w u x w D M w x x x x x -=∂∂-=∂∂+∂∂-======0220222200)(0；OC 边：0)(00220222200=∂∂-=∂∂+∂∂-======y y y y y y wD x w u y w D M w ；BC 边：00=∂∂===ax a x xww ；AB 边：0)(2222=∂∂+∂∂-===b y by yx wu y w D M0])2([)(2333=∂∂∂-+∂∂-=∂∂+==by by yx y y x w u y w D xM Q2-2 如图2-2所示，矩形薄板OA 边和OC 边为简支边，AB 和BC 为自由边，在点B 受向下的横向集中力P 。

试证w mxy =可作为该薄板的解答，并确定常数m 、内力及边界处反力。

解：mxy w =满足平衡微分方程0/4==∇D q wOC 边上：0)(0022220＝；==∂∂+∂∂-=y y x wu y w D wOA 边上：0)(0022220＝；==∂∂+∂∂-=x x y wu x w D wAB 边上：0])2([0)(23332222=∂∂∂-+∂∂-=∂∂+∂∂-==by b y y x wu y w D x w u y w D ；BC 边上：0])2([0)(23332222=∂∂∂-+∂∂-=∂∂+∂∂-==ax a x y x wu x w D y w u x w D ；在B 点上：P m u D y x wu D by a x -=--=∂∂∂--==)1(2)()1(2,2)1(2u D Pm -=⇒所以)1(2u D Pxyw -=0)(2222=∂∂+∂∂-=y wu x w D M x ；0)(2222=∂∂+∂∂-=x w u y w D M y ；2)1(2P y x w u D M xy-=∂∂∂--= ；02=∇∂∂-=w xD Q x ；02=∇∂∂-=w y D Q y P R R P y x wu D R O C AA ==-=∂∂∂--=；)()1(222-3 如图2-3所示，半椭圆形薄板，直线边界为简支边，曲线边界ACB 为固支边，承受横向载荷0q=q xa 。

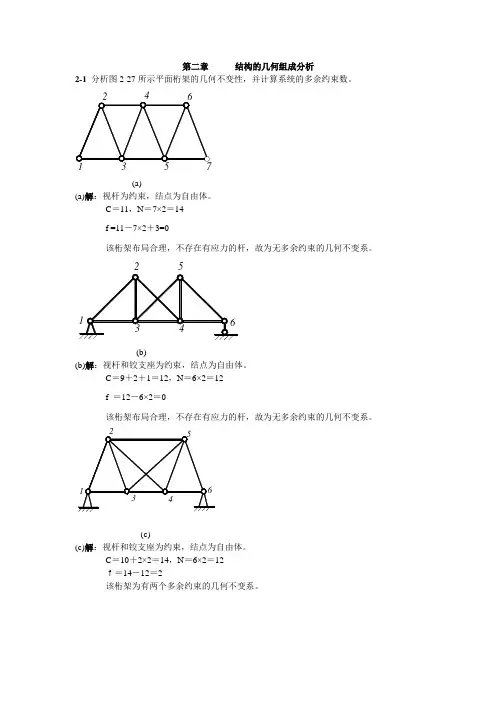
西北工业大学航空学院结构力学课后题答案第二章结构的几何组成分析

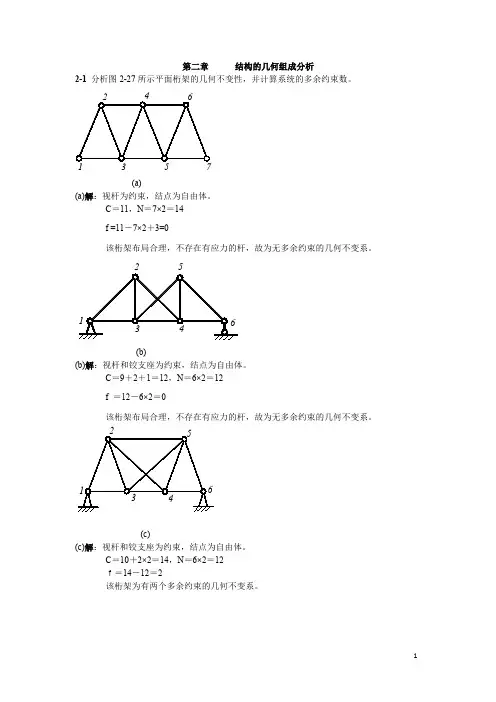
第二章 结构的几何组成分析2-1 分析图2-27所示平面桁架的几何不变性，并计算系统的多余约束数。

3571(a)(a)解：视杆为约束，结点为自由体。

C ＝11，N ＝7×2＝14f =11－7×2＋3=0该桁架布局合理，不存在有应力的杆，故为无多余约束的几何不变系。

(b)(b)解：视杆和铰支座为约束，结点为自由体。

C ＝9＋2＋1＝12，N ＝6×2＝12f ＝12－6×2＝0该桁架布局合理，不存在有应力的杆，故为无多余约束的几何不变系。

(c)(c)解：视杆和铰支座为约束，结点为自由体。

C ＝10＋2×2＝14，N ＝6×2＝12ｆ＝14－12＝2该桁架为有两个多余约束的几何不变系。

1217(d)(d)解：视杆和铰支座为约束，结点为自由体。

C ＝30＋3＝33，N ＝17×2＝34ｆ＝33－34＝-1故该桁架为几何可变系。

8(e)(e)解：视杆为约束，结点为自由体。

C ＝13，N ＝8×2＝16ｆ＝13－16＋3＝0将1-2-3-4、5-6-7-8看作两刚片，杆3-6、杆2-7、杆4-5相互平行，由两刚片原则知，为瞬时可变系统。

6(f)(f)解：视杆和固定铰支座为约束，结点为自由体。

C ＝22＋3×2＝28，N ＝14×2＝28ｆ＝28－28＝0将12-13-14、7-11-12、1-2-3-4-5-6-7-8-9-10看作三刚片，三刚片由铰7、铰12、铰14连结，三铰共线，故该桁架为瞬时可变系统。

(g)(g)解：视杆和固定铰支座为约束，结点为自由体。

C＝24＋4×2＝32，N＝16×2＝32ｆ＝32－32＝0由于杆15-14-3、杆12-11-4、杆9-5相交于一点，故该桁架为瞬时可变系。

(h)(h)解：视杆和固定铰支座为约束，结点为自由体。

C＝12＋2×2＝16，N＝8×2＝16ｆ＝16－16＝0该桁架布局合理，加减二元体之后，无有应力的杆，故该桁架为无多余约束的几何不变系。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。