下载文档原格式
西工大飞行器结构力学电子教案第一章：绪论1.1 课程简介1.2 飞行器结构力学的研究对象和内容1.3 飞行器结构力学的应用领域1.4 学习方法和教学要求第二章：飞行器结构的基本受力分析2.1 概述2.2 飞行器结构的受力分析方法2.3 飞行器结构的受力类型及特点2.4 飞行器结构的基本受力分析实例第三章：飞行器结构的弹性稳定性分析3.1 概述3.2 弹性稳定性的判别准则3.3 飞行器结构弹性稳定性分析方法3.4 飞行器结构弹性稳定性分析实例第四章：飞行器结构的强度分析4.1 概述4.2 飞行器结构强度计算方法4.3 飞行器结构材料的力学性能4.4 飞行器结构强度分析实例第五章：飞行器结构的刚度分析5.1 概述5.2 飞行器结构刚度计算方法5.3 飞行器结构刚度分析实例5.4 飞行器结构刚度优化设计第六章：飞行器结构的疲劳分析6.1 概述6.2 疲劳寿命的计算方法6.3 疲劳裂纹扩展规律6.4 飞行器结构疲劳分析实例第七章：飞行器结构的断裂力学分析7.1 概述7.2 断裂力学的基本概念7.3 断裂判据和裂纹扩展规律7.4 飞行器结构断裂力学分析实例第八章：飞行器结构的动力学分析8.1 概述8.2 飞行器结构动力学的基本方程8.3 飞行器结构的动力响应分析8.4 飞行器结构动力学分析实例第九章：飞行器结构复合材料分析9.1 概述9.2 复合材料的力学性能9.3 复合材料结构分析方法9.4 飞行器结构复合材料分析实例第十章：飞行器结构力学工程应用案例分析10.1 概述10.2 飞行器结构力学在飞机设计中的应用10.3 飞行器结构力学在航天器设计中的应用10.4 飞行器结构力学在其他工程领域的应用重点和难点解析重点环节一：飞行器结构的基本受力分析补充和说明：飞行器结构的基本受力分析是理解飞行器结构力学的基础，需要掌握各种受力类型的特点和分析方法，并通过实例加深理解。
重点环节二：飞行器结构的弹性稳定性分析补充和说明：弹性稳定性是飞行器结构设计中的关键问题，需要理解判别准则，掌握分析方法，并通过实例了解实际应用。
【大学课件】飞机结构力学电子教学教案第一章：课程介绍与基本概念1.1 课程背景与意义介绍飞机结构力学的发展历程及其在航空航天领域的重要性。
强调本课程的目标和意义，即培养学生对飞机结构力学的理解和应用能力。
1.2 课程内容概述概述课程的主要内容，包括飞机结构的基本类型、受力分析、材料力学性质等。
1.3 教学方法与要求介绍本课程的教学方法，包括课堂讲解、案例分析、实验实践等。
对学生的学习要求进行说明，包括课堂参与、作业完成、期末考试等。
第二章：飞机结构的基本类型与特点2.1 飞机结构的基本类型介绍飞机结构的主要类型，包括梁、板、壳、框架等。
2.2 飞机结构的特点分析飞机结构的特点，包括轻质、高强、耐腐蚀、可制造性等。
2.3 实际案例分析通过实际案例分析，让学生更好地理解飞机结构的基本类型和特点。
第三章：飞机结构的受力分析3.1 飞机结构的受力类型介绍飞机结构所受的各种力，包括重力、气动力、惯性力等。
3.2 飞机结构的受力分析方法介绍飞机结构的受力分析方法，包括静态分析、动态分析等。
通过实际案例分析，让学生更好地理解飞机结构的受力分析方法和过程。
第四章：飞机结构的材料力学性质4.1 材料的应力与应变介绍材料的应力与应变概念，包括应力应变关系、弹性模量等。
4.2 材料的屈服与破坏分析材料的屈服条件、破坏形式及其影响因素。
4.3 材料的选用与匹配介绍飞机结构材料的选择原则，包括强度、刚度、耐腐蚀性等。
第五章：飞机结构的设计与优化5.1 飞机结构设计的基本原则介绍飞机结构设计的基本原则，包括安全性、可靠性、经济性等。
5.2 飞机结构设计的步骤与方法详细介绍飞机结构设计的步骤与方法，包括需求分析、方案设计、详细设计等。
5.3 飞机结构的优化方法介绍飞机结构的优化方法，包括拓扑优化、尺寸优化等。
第六章：飞机结构的连接与接头设计6.1 飞机结构连接的类型介绍飞机结构连接的类型，包括螺栓连接、焊接连接、粘接连接等。
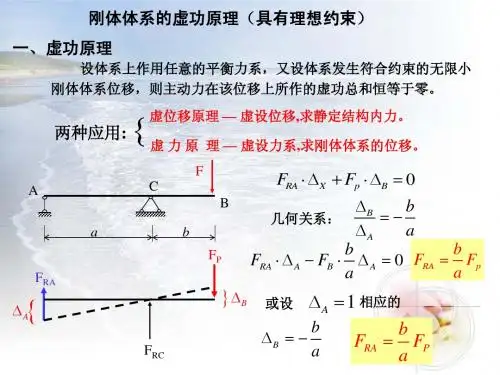
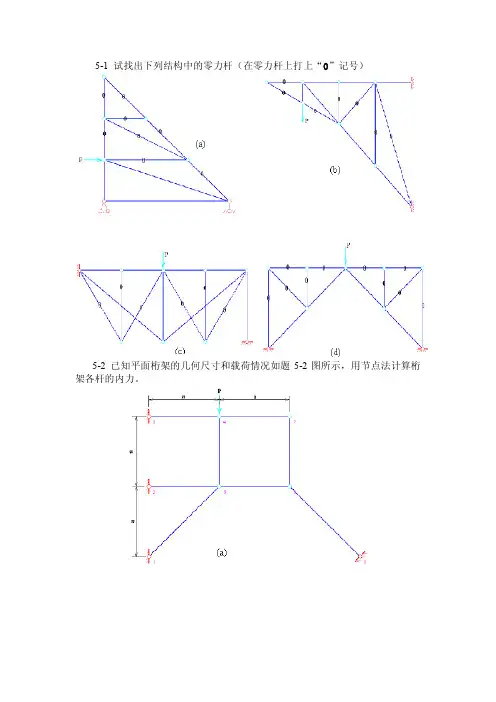
5-1试找出下列结构中的零力杆（在零力杆上打上“0”记号）5-2 已知平面桁架的几何尺寸和载荷情况如题5-2图所示，用节点法计算桁架各杆的内力。
解：(a)、零力杆：74，76，65，68，43分析节点4，得P N -=45分析节点5，得 ２－ １P N P N ==552,(b)、零力杆：26，61，63，48，83，85，37，71分析节点7：P N -=75 分析节点5：5254P N =1221233234434554N N N N N N N N =======(c)、支座反力：均为0分析节点1： P N P N 2,31512-== 分析节点2： P N P N 2,32523== 分析节点3： P N 235-= 分析节点4： 04543==N N (d)、零力杆：12，15，52，83，43，49支座反力：P R P R P R y x y 3.1,8.0,3.2223=-==分析节点5： P N 8.056-=分析节点6： P N P N -=-=6267,8.0 分析节点9： P N P N 6.0,26.09893=-= 分析节点8： P N 6.087=分析节点3： P N P N 1.1,27.13237=-= 分析节点7： P N 23.072-=5-3 用分解成平面桁架的方法求如题5-3图所示空间桁架各杆的内力。
解：零力杆：26，48，34，24，28122152316213337317383N P a N P P cN P N P N P N P NP ==-=-=-===-３ 5-4 已知平面桁架的几何尺寸和受载情况如题5-4图所示。
求图中用粗线所示的杆件①，②，③的内力。
解：(a)、零力杆如图所示1340,3P M N ==∑由得 3210,M N P ==-∑由得310,3y F N P ==∑由得 (b)、2140,2M N P ==∑由得230,x F N P ==-∑由得250,y F N ==∑由得(c)、支座反力：均为0，结构简化为：PN F P N F PN M x y 31,032,032,03213====-==∑∑∑得由得由得由5-5 求如题5-5图所示平面桁架的内力。
飞机结构力学课程辅导提纲军区空军自考办第一章结构的组成原理一、内容提要1、飞机结构力学的任务飞机结构力学是研究飞机结构组成规律以及在给定外荷载作用下计算结构内力与变形的一门学科。
结构元件之间无相对刚体位移的性质叫几何不变性；结构能维持其与坐标系统位置的关系，即系统具有足够的支座连接，以保证其位置固定不变的性质叫不可移动性。
飞机结构受力系统显然应具有几何不变性和不可移动性。
2、飞机结构力学的基本假设（1）小变形假设：认为结构在载荷作用下变形很小，可以认为它不影响结构的几何形状。
（2）线性弹性假设：认为结构为线弹性系统。
线性：结构或元件的内力与变形的关系为线性关系（直线变化）。
弹性：结构或元件在载荷作用下产生内力与变形，在载荷卸去后结构或元件恢复到原始状态，不留残余变形。
3、实际受力系统按照其几何形状的变化可分为三种情况（1）几何可变系统：在外力作用下不能保持原来的几何形状的结构。
（2）几何不变系统：无论在何种外力作用下，都能保持原有几何形状的结构。
（3）瞬时几何可变系统：在受力的瞬间会发生变形，但随着变形的出现，结构又转化成几何不变系统而使形变不能再继续下去。
由以上的分析看出，对于一个承力结构来说，只有几何不变的结构才能承担任意形式的外载荷。
几何可变和瞬时可变系统都是绝不允许的。
4、自由度与约束（1）自由度：决定某物体在坐标系中位置所需的独立变量数。
故平面内一点有两个自由度；平面内的一根杆子或平面几何不变系统只需要三个独立变量数：x,y与夹角α就能确定它的位置,故一根杆子或一个几何不变系统具有三个自由度。
同理，空间一点有三个自由度，一个刚体或空间几何不变系统有六个自由度。
（2）约束：减少自由度的装置。
在结构力学中，为分析的方便，通常把节点看作为自由体，把杆子看作为约束。
无论是平面系统还是空间系统一根两端带铰链的杆子都相当于一个约束。
5、几何不变的条件系统内的约束数大于活等于系统内的自由度数，即0C≥-N式中C是约束数，N是自由数。
