- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、复变函数积分的定义
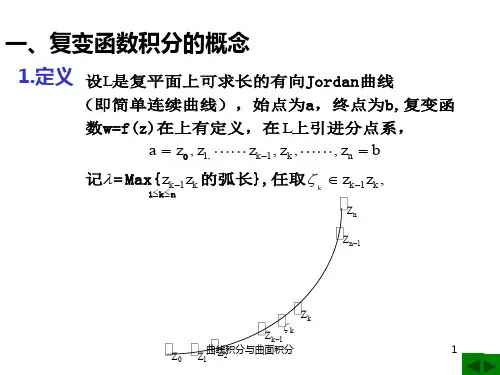
设在复平面 C 上有一条连接 z 0 及 Z 两点的简单曲 线 C 。设 f(z)=u(x,y)+iv(x,y) 是在 C 上的连续函数。其中 u(x,y)及v(x,y)是f(z)的实部及虚部。 把曲线C用分点 z0 , z1 , z2 ..., zn 1 , zn Z
C
f ( z )dz 0 f ( z )dz f ( z )dz 0 f ( z )dz f ( z )dz
C1 C2 C1 C2
b
a
C1
结论2: 周线C : f ( z )dz 0 C 函数f(z)的积分与路径无关,
目的
研究复积分与路径的无关性:
k
zk
C
z1
z0
复变函数的积分
分实部与虚部,有 n 1
[u (
k 1
k
k
, k ) iv( k , k )][( xk 1 xk ) i ( yk 1 yk )]
n 1
或者
u (
k 1 n 1 k 1
n 1
, k )( xk 1 xk ) v( k , k )( yk 1 yk )
max{| zk 1 zk | ( xk 1 xk ) ( yk 1 yk )
2 2
0 | k 0,1,2,..., n 1} 0
时,上面的四个式子分别有极限:
u( x, y)dx, v( x, y)dy, v( x, y)dx, u( x, y)dy,
C f ( z)dz C f ( z)dz, (4) 积分是在相反的方向上取的。
复变函数积分的性质:
如果C是一条简单闭曲线,那么可取C上任意一 点作为取积分的起点,而且积分当沿 C 取积分 的方向改变时,所得积分相应变号。 ( 5 )如果在 C 上, |f(z)|<M ,而 L 是曲线 C 的长 度,其中M及L都是有限的正数,那么有,
c
f ( z )dz 0.
此定理常称为柯西积分定理. 定理中的 C 可以不是简单 曲线.
古萨介绍
柯西介绍
C
D
3.2.2 Cauchy定理的推广 推论3.4 柯西定理
设D为单连通域 ,如果函数 f ( z ) A( D ) 对 D 内的任何一条闭曲线 C , 有:
不必是简 单闭曲线
转换为研究函数沿着周线的积分为零:
观察上节例3.1
虽然在除去 z0 的 C 的内部函数处处解析, 但此区域已不是单连通域.
1 观察上 被积函数当n 0 时为 , 节例3.2 z z0 它在以 z0为中心的圆周 C 的内部不是处处解析的, 1 此时 dz 2i 0. c z z 0
证明:因为
n 1 k 1
| f ( z )dz | ML
C
n 1
| f ( k )( zk 1 zk ) | M | zk 1 zk | ML
k 1
两边取极限即可得结论。
例1
例1、设C是连接
C
z 0 及Z两点的简单曲线,那么
0
dz Z z
1 2 2 Czdz 2 (Z z0 ). 如果是C闭曲线,即 Z z0 ,那么积分都是 零。
解 C : z z0 re i
0 2
y
z z0 re i
i 2 dz ire d n 1 n 1 i ( n 1 ) C (z z ) 0 r e 0
z
o
z0
r
C
x
2
0
i r n e in
i 2 d 2i n0 0 d i 2 n 0 (cosn i sinn )d 0 n 0 r
f ( z ) 1或z 在复平面内处处解析, f ( z )dz =0
C
由以上讨论可知, 积分是否与路线有关, 可 能决定于被积函数的解析性及区域的连通性. 受此启发,Cahchy与1825年给出如下定理
定理3.3-0 设D为单连通域 ,函数 f ( z ) 在D 内满足 : ( 1) f ( z ) A( D ), ( 2 ) f ( z ) C ( D ), 对 D 内的任何一条周线 C , 有:
C3
C2
解 1)C1 : z (1 i )t
1 C 0
0 t 1
1 0
o
x
zdz (t it )(1 i )dt
C C2 1 C3 1
0
2tdt 1
2)C2 : z t 0 t 1 C3 : z 1 it 0 t 1
zdz zdz zdz 1 1 tdt (1 it )idt ( i ) 1 i 2 2
c
f ( z )dz 0.
1900,法国数学家Goursat给出如下定理: 如果f(z)A(D) f'(z) A(D) f'(z) C(D),这 样就得到了定理3.3
3.3.单连通区域的Cauchy积分定 理
定理3.3 柯西-古萨基本定理
设D为单连通域 ,如果函数 f ( z ) A( D ) 对 D 内的任何一条周线 C , 有:
第三章 复变函数的积分
同微积分一样,在复变函数中,积分 法也是研究复变函数性质十分重要的方法.
在解决实际问题中也是有力的工具. 本章先介绍复变函数积分的概念,性质和计
算方法然后介绍关于解析函数积分的柯西-
古萨基本定理及其推广,有了这些基础,我
们建立柯西积分公式,最后证明解析函数的
导数仍是解析函数,从而导出高阶导数公式
c
f ( z )dz 0.
推论3.5
柯西定理
设D为单连通域 ,如果函数 f ( z ) A( D ) f ( z ) 在 D 内的积分与路径无关,即对任给的z0 , z1积分
z0
z1
f ( z )dz
的值,不依赖于D内连接起点a与终点b的曲线的形状
与定理3.3等价的形式是: 定 理 3.3
0
i
ie d i dt i
i
0
2)C2 : z e i , 0.
zdz e
C2
i
ie d i二节 柯西积分定理
3.2.1 Cauchy积分定理
3.2.2 Cauchy定理的推广 3.2.3 复周线情形的Cauchy定理 3.2.4 不定积分 3.2.4 小结与思考
目的
引言:
研究复积分与路径的无关性:
由例3.1受到的启发积分与路径无关与函数沿 着围线的积分值为零有何关系 首先:若复积分与路径无关,则对任意围线C, C2 在其上任取两点按a(起点),b(终点) C 将曲线C分成两部分 C C1 C2 a 因为积分与路径无关,所以: C 1 f ( z ) dz f ( z ) dz
复变函数的积分
x (t ), y (t )(t0 t T ) 如果C是简单光滑曲线:
,并且 t0及T相应于z0及Z ,那么上式右边的 积分可以写成黎曼积分的形式,例如其中第一 个可以写成 T u( , ) ' (t )dt
t0
因此,我们有
C
f ( z )dz [u ( , ) iv( , )][ ' (t ) i ' (t )]dt
C1 C2
b
f ( z )dz
C
C1
f ( z )dz
C2
f ( z )dz 0
结论1:若函数f(z)的积分与路径无关,
周线C : f ( z )dz 0
C
反之:若对任意围线C,f(z)沿着C的积分为零,若复 积分与路径无关, 则对任意两条以 a为起点,b为终点的曲线C1,C2,令: C2 C C1 C2 则C是周线,从而:
分成n个更小的弧,在这里分点 zk (k 0,1,2,..., n)
是在曲线C上按从 z 0 到Z的次序排列的。
如果 k 是 z k 到 z k 1 的弧上任意一点,那么考虑和式
f (
k 1
n 1
k
)( zk 1 zk )
复变函数的积分
zn Z
z n 1 z k 1
k 1 n 1
i[ v( k , k )( xk 1 xk ) u ( k , k )( yk 1 yk ),
k 1
在这里 xk、yk 及 k、 k 分别表示的 zk 与 k 实部与虚部。
复变函数的积分
按照关于实变函数的线积分的结果,当曲线 C 上的分点个数无穷增加,而且
2i dz dz 1 n n 1 C (z z ) z z0 r ( z z ) 0 0 0
n0 n0
这个结果与半径 r及z0无关, 这个结果 以后经常用到, 应记住.
例4 计 算 zdz 的值
C
y
z0 1 i
C1
1)C C1 Oz0 2)C C 2 C 3 (见 图)
t0
T
复变函数的积分
我们可以看到,把dz形式地换成微分,就直接 得到上式,因此有
C
f ( z )dz f ( z (t )) z ' (t )dt
t0
T
当是分段光滑简单曲线时,我们仍然可以得到 这些结论。
2 复变函数积分的性质:
复变函数积分的基本性质:设 f(z)及g(z)在简单 曲线C上连续,则有 (1 ) C f ( z)dz C f ( z)dz, 其中是一个复常数;