新人教数学 7年级下：作业40 §9.4 课题学 利用不等关系分析比赛.pdf

9.4利用不等关系剖析竞赛学习目标1、认识部分体育竞赛项目判断输赢的规则，复习并稳固不等式的有关知识；2、以体育竞赛问题为载体，研究实质问题中的不等关系，进一步领会利用不等式解决问题的基本过程；3、在利用不等关系剖析竞赛结果的过程中，提升剖析问题、解决问题的能力，发展逻辑思想能力和有条理表达思想过程的能力；4、感觉数学的应用价值，培育用数学目光看世界的意识，指引学生关注生活、关注社会．学习要点与难点要点：利用不等关系剖析展望竞赛结果难点：在开放的问题情境中促进学生的思想从无序走向有序；在剖析、解决问题的过程中发展学生用数学目光看世界的主动性学习过程一、课前预习部分多媒体展现有关雅典奥运会射击竞赛的场景，从而引出问题1：某射击运动员在一次竞赛中前 6 次射击共中 52 环，假如他要打破89 环（ 10 次射击）的纪录，第 7 次射击不可以少于多少环？引出话题后，因为问题自己其实不复杂，在同学解决此问题后，教师适合予以夸奖后应实时将问题变维发散，在研究中将思想引向深人．（1）假如第 7 次射击成绩为 8 环，最后三次射击中要有几次命中10 环才能破纪录？（2）假如第 7 次射击成绩为 10 坏，最后三次射击中能否一定起码有一次命中 10 环才能破纪录？二、讲堂研究部分（先独立达成，再小组议论完美答案）媒体展现多种场景，除了射击竞赛，在竞技场上还有许很多多动人心魄、出色纷呈的竞赛，同学们有兴趣对他们也进行一些剖析吗？问题 2：有 A ， B，C，D，E 五个队分同一小组进行单循环赛足球竞赛，争夺出线权．竞赛规则规定：胜一场得 3 分，平一场得 1 分，负一场得 0 分，小组中名次在前的两个队出线，小组赛结束后， A 队的积分为 9 分．你以为 A 队能出线吗？请说明原因．学生充足发布建议，在争辩中发现此问题不可以混为一谈，需要考虑其余队的状况，于是形成问题假定：(1)假如小组中有一个队的战绩为全胜， A 队可否出线？(2)假如小组中有一个队的积分为10 分， A 队可否出线？(3)假如小组中积分最高的队积9 分， A 队可否出线？在议论沟通中形成问题、解决问题，在解决问题中自然波及足球竞赛的有关规则．三、自我检测反应部分（独立完结婚自着手做一做）1、必做题：．必做题：(1)足球竞赛的计分规则为：胜一场得 3 分，平一场得 1 分，负一场得 0 分一个队打 14 场竞赛负 5 场共得 19 分．那么这个队胜了几场？(2)甲、乙、丙三位同学进行立定跳远竞赛，每人跳一次称为一轮，每轮按名次高低分别得 3,2,1 分（没有并列名次）．他们进行了五轮竞赛，结果甲共得14分；乙第一轮得 3 分，第二轮得 1 分，且总分最低．那么丙获得的分数是（）A.8分B.9分C.10分D.11分(3)教科书 157 页复习题 9 第 11题．四、小结与反省：本节课我学会了：；我的疑惑是：.第二课时复习引入在上节课中，我们曾利用不等关系对一些体育竞赛的结果进行剖析，初步感触了剖析解决此类问题的思想方法。

人教版七年级数学下册《9.4 利用不等关系分析竞赛》教学设计PPT课件导学案教案人教版七年级数学下册《9.4 利用不等关系分析竞赛》教学设计PPT课件导学案教案课题： 9.4 利用不等关系分析竞赛教学目标一、了解部份体育竞赛项目判定输赢的规那么，温习并巩固不等式的相关知识；二、以体育竞赛问题为载体，探讨实际问题中的不等关系，进一步体会利用不等式解决问题的大体进程；3、在利用不等关系分析竞赛结果的进程中，提高分析问题、解决问题的能力，进展逻辑思维能力和有层次表达思维进程的能力；4、感受数学的应用价值，培育用数学目光看世界的意识，引导学生关注生活、关注社会．教学难点在开放的问题情境中促使学生的思维从无序走向有序；在分析、解决问题的进程中进展学生用数学目光看世界的主动性知识重点利用不等关系分析预测竞赛结果。

教学进程（师生活动）设计理念创设情境引出话题多媒体展现有关雅典奥运会射击竞赛的场景，进而引出问题1：某射击运动员在一次竞赛中前6次射击共中52环，若是他要打破89环（10次射击）的纪录，第7次射击不能少于多少环？在真实、熟悉的背景中切入话题，激发学生数学学习的爱好牛刀小试初享成功引出话题后，由于问题本身并非复杂，在同窗解决此问题后，教师适当予以夸奖后应及时将问题变维发散，在探讨中将思维引向深人．（1）若是第7次射击成绩为8环，最后三次射击中要有几回命中10环才能破纪录？（2）若是第7次射击成绩为10坏，最后三次射击中是不是必需至少有一次命中10环才能破纪录？初一学生好胜心强，课堂比较活跃，但这只是表面的繁荣．教师在初享成功后，要利用带动的课堂气氛，使学生顺利以研究者的姿态进入问题再生与问题解决中，从而有利于问题2,3的探讨．扩大视野乘胜追击媒体展现多种场景，除射击竞赛，在竞技场上还有许许多多扣人心弦、出色纷呈的竞赛，同窗们有爱好对他们也进行一些分析吗？问题2：有A，B，C，D，E五个队分同一小组进行单循环赛足球竞赛，争夺出线权．竞赛规那么规定：胜一场得3分，平一场得1分，负一场得0分，小组中名次在前的两个队出线，小组赛终止后，A队的积分为9分．你以为A 队能出线吗？请说明理由．学生充分发表意见，在辩论中发觉此问题不能一概而论，需要考虑其他队的情形，于是形成问题假设：(1)若是小组中有一个队的战绩为全胜，A队可否出线？(2)若是小组中有一个队的积分为10分，A队可否出线？(3)若是小组中积分最高的队积9分，A队可否出线？在讨论交流中形成问题、解决问题，在解决问题中自然涉及足球竞赛的相关规那么．教材中的问题已经给出了探讨的要紧步骤，对试探进程做了一些提示，同时这些提示也限制了学生的思维．如此的探讨仍是属于较低层次的，而假设在背景中直接提出问题，那么问题就有了必然的开放性，给学生以创新的空间，使学生更能体会课题的味道，有利于课后自己从其他背景中提出问题并尝试解决．总结与作业问题反思归纳总结一、在上述利用不等关系分析竞赛的问题解决中，咱们是如何进行试探的？二、通过本节课的学习，你有哪些感受或体会。

人教版数学七年级下册第58课时《9.4利用不等关系分析比赛（一）》教学设计一. 教材分析《9.4利用不等关系分析比赛（一）》是人教版数学七年级下册第五章第九节的内容。

本节课主要让学生学会利用不等关系分析比赛中的各种问题，培养学生运用不等式解决实际问题的能力。

教材通过具体的比赛场景，引导学生理解不等式的含义，掌握不等式的解法，并能够运用不等式解决实际问题。

二. 学情分析学生在七年级上学期已经学习了不等式的基本概念和性质，对于不等式的解法有一定的了解。

但是，对于如何将实际问题转化为不等式，以及如何运用不等式分析比赛中的问题，学生可能还存在一定的困难。

因此，在教学过程中，教师需要通过具体例子，引导学生将实际问题转化为不等式，并运用不等式进行分析。

三. 教学目标1.理解不等式在比赛中的应用，能够将实际问题转化为不等式。

2.掌握不等式的解法，能够运用不等式分析比赛中的各种问题。

3.培养学生的逻辑思维能力和解决实际问题的能力。

四. 教学重难点1.教学重点：引导学生理解不等式在比赛中的应用，掌握不等式的解法。

2.教学难点：如何将实际问题转化为不等式，以及如何运用不等式分析比赛中的问题。

五. 教学方法1.情境教学法：通过具体的比赛场景，引导学生理解不等式在比赛中的应用。

2.案例教学法：通过分析具体的比赛案例，让学生掌握不等式的解法。

3.小组合作学习：让学生在小组内讨论如何将实际问题转化为不等式，并运用不等式进行分析。

六. 教学准备1.准备相关的比赛案例，用于引导学生分析和讨论。

2.准备多媒体教学设备，用于展示比赛场景和案例。

七. 教学过程1.导入（5分钟）教师通过展示一些比赛场景，如篮球比赛、跑步比赛等，引导学生思考比赛中的不等关系。

让学生举例说明比赛中的不等关系，并尝试将其转化为不等式。

2.呈现（10分钟）教师呈现一些具体的比赛案例，如篮球比赛中的得分、篮板、助攻等数据，让学生尝试分析这些数据中的不等关系，并将其转化为不等式。

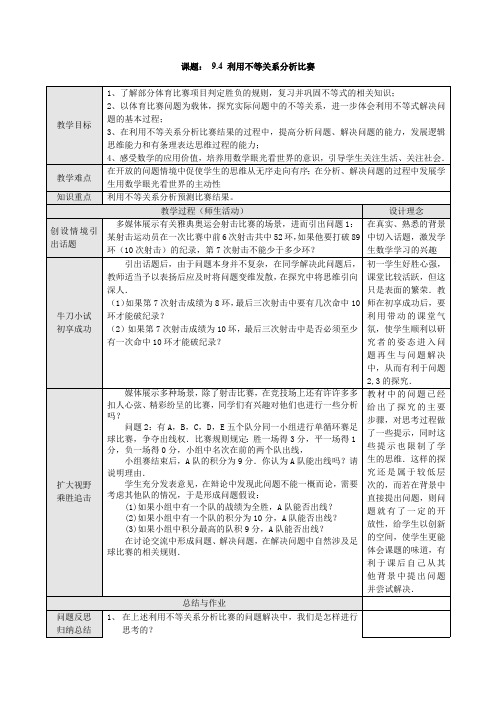
9.4 课题学习 利用不等关系分析比赛班级 学号 姓名一、利用不等关系分析射击比赛射击比赛积分规定：射击比赛的成绩取决于环数的高低，环数越大成绩越好，（如10环比9环成绩好）几次累计环数为运动员的总成绩。

例1：教科书P149问题1方法指导：本题的主要不等关系是此运动员的总成绩＞89环分析讨论1：设要有x 次击中10环才能破记录，10+52+10x ＞89 解得 x ＞1029 又x 是正整数， ∴ x =3 分析讨论2：设最后要有x 次击中10环才能破记录，其余最高为9环。

10+52+10x+9（3－x ）＞89 解得 x ＞0∴ 至少有1次击中10环才能破记录。

二、利用不等关系分析足球比赛足球比赛积分规定：胜一场得3分，平一场得1分，负一场得0分.按积分多少排名次，积分相同的两队，净胜球多的队名次在前，积分、净胜球都相等的两队，进球数多的队名次在前。

例2：教科书P149问题2分析提示：1、若有n 支球队进行单循环比赛，则总的比赛场数是 2)1(-n n 2、讨论1：设A 队积9分胜x 场，平y 场，则93=+y x ① ;其中，非负整数x,y 满足y x +≤4 ②由①、②得，x=3,y=0∴ A 队3胜，0平，1负.讨论2：如有一个队胜4场，则它积12分并且名列小组第一，不妨设这个队为B 队，A 队能否出线取决于C 、D 、E 三队中是否有积分不少于9分的队，分析这三队中任何一队的积分数m 应满足m ＜9，从而A 队积9分时能出线。

讨论3：如有一个队（不妨设B 队）积10分，进行类似于（1）的讨论可知B 队三胜一平，由于A 队为三胜一平，则总积分最多可为29分，其他队中可能有一个最多为两胜一平，故A 队能出线；讨论4：如积分最高的队积9分，则积9分的队可能有3个。

当积9分的队为2个时，A 队一定出线；当积9分的队为3个时，A 队不一定出线；（5）、若A 队积10分，则A 队一定出线，因为若其他队中最好成绩大于10分时，则其他三队积分一定小于10，故A 队能出线。

新人教版七年级下册数学教案第九章不等式与不等式组阅读与思考：利用不等关系分析比赛（第一课时）第一篇：新人教版七年级下册数学教案第九章不等式与不等式组阅读与思考：利用不等关系分析比赛(第一课时)阅读与思考：利用不等关系分析比赛教学目标1、了解部分体育比赛项目判定胜负的规则，复习并巩固不等式的相关知识；2、以体育比赛问题为载体，探究实际问题中的不等关系，进一步体会利用不等式解决问题的基本过程；3、在利用不等关系分析比赛结果的过程中，提高分析问题、解决问题的能力，发展逻辑思维能力和有条理表达思维过程的能力；4、感受数学的应用价值，培养用数学眼光看世界的意识，引导学生关注生活、关注社会．教学重点：利用不等关系分析预测比赛结果。

教学难点：在开放的问题情境中促使学生的思维从无序走向有序；在分析、解决问题的过程中发展学生用数学眼光看世界的主动性教学过程（师生活动）创设情境：引出话题多媒体展示有关雅典奥运会射击比赛的场景，进而引出问题1：某射击运动员在一次比赛中前6次射击共中52环，如果他要打破89环（10次射击）的纪录，第7次射击不能少于多少环？牛刀小试初享成功引出话题后，由于问题本身并不复杂，在同学解决此问题后，教师适当予以表扬后应及时将问题变维发散，在探究中将思维引向深人．（1）如果第7次射击成绩为8环，最后三次射击中要有几次命中10环才能破纪录？（2）如果第7次射击成绩为10坏，最后三次射击中是否必须至少有一次命中10环才能破纪录？扩大视野乘胜追击媒体展示多种场景，除了射击比赛，在竞技场上还有许许多多扣人心弦、精彩纷呈的比赛，同学们有兴趣对他们也进行一些分析吗？问题2：有A，B，C，D，E五个队分同一小组进行单循环赛足球比赛，争夺出线权．比赛规则规定：胜一场得3分，平一场得1分，负一场得0分，小组中名次在前的两个队出线，小组赛结束后，A队的积分为9分．你认为A队能出线吗？请说明理由．学生充分发表意见，在辩论中发现此问题不能一概而论，需要考虑其他队的情况，于是形成问题假设：(1)如果小组中有一个队的战绩为全胜，A队能否出线？(2)如果小组中有一个队的积分为10分，A队能否出线？(3)如果小组中积分最高的队积9分，A队能否出线？在讨论交流中形成问题、解决问题，在解决问题中自然涉及足球比赛的相关规则．总结:1.归纳总结在上述利用不等关系分析比赛的问题解决中，我们是怎样进行思考的？2.通过本节课的学习，你有哪些感受或体会。

数学初一下人教新资料9.4利用不等关系分析比赛教案教学目标1.综合利用不等关系及所学知识解决实际问题；2.能正确地进行分析，会建立相应的数学模型，从而培养学生的推理能力，并能有条理地阐述自己的观点；3.通过小组活动，让学生学会与他人合作，并能结合具体的体育比赛提出问题、解决问题；4.树立数学的意识，培养探究精神以及互相协作的态度。

教学重点利用不等式刻画事物间的相互关系。

教学难点对实际问题背景的理解，如何将实际问题数学化。

教学过程【一】复习与回顾1.不等式组在实际问题中应用，解题时应注意哪些问题？2.如何解关于不等式组的应用题？【二】看一看阅读课本P149第一段，结合学生课前收集的资料，提出问题：1.两队比赛，一队胜另一队就会有什么结果？这说明了什么？2.对比赛结果的分析，经常要考虑哪些关系？〔学生针对问题进行小组学习、交流探索、回答以下问题〕【三】问题探究问题1.某射击运动员在一次比赛中前6次射击共中52环，如果他要打破89环〔10次射击〕的记录，第7次射击不能少于多少？讨论：〔1〕如果第7次射击成绩为8环，最后三次射击要有几次命中10环方能破记录？〔2〕如果第7次射击成绩为10环，最后三次射击是否必须至少有一次命中10环才有可能破记录？问题2.有A、B、C、D、E五个队分在同一小组进行单循环足球比赛，争夺出线权，比赛规那么：胜一场得3分，平一场得1分，负一场的0分，小组中名次在前的两个队出线。

小组赛结束后，A队的积分为9分。

讨论：〔1〕A队的战绩是几胜几平几负？〔2〕如果小组中有一队的战绩为全胜，A队能否出线？如果小组中有一队的积分为10分，A队能否出线？9分呢？〔3〕如果A队的积分为10分，它能出线吗？〔教师出示问题，学生以组为单位，阅读分析，并在小组讨论的基础上，选定一个问题进行探究。

教师参与各组的讨论，适时给予指导。

学生小组讨论，积极探究解决问题的方法。

〕教学时教师重点关注：〔1〕学生能否理解题意，并准确挖掘出问题中的隐含条件，从而运用不等式描述问题中的不等关系，得出正确结论。

《课题学习——利用不等关系剖析竞赛》教学设计程目一、知与技术目学会运用不等式及不等式一些体育比的行剖析,? 学生感知生活离不开数学, 学数学知是更好地解决服.二、程与方法目出详细事例学生行剖析 , 激学生体育事的关怀和戴 , 体育成的劣与公民素关系的理解 , 激学生的国精神和主人翁意 .三、感情度与价目体育事的展与否从某方面来, 代表一个国家的盛, 代表一个国家在国上的地位和著名度 , 体育健儿在上国争光, 我有学他的精神的必需性,? 同要能利用所学不等式,行剖析、求解.一、情境, 入新据年代日北京青年道球推出新措吸引球迷. 撤消起落 , 区分南北区 , 增添球和比次 , 撤消冠名, 立“新言人制度”和主客金制度，“至尊戒”等⋯⋯新季 ?不一样过去的看点一个又一个, 全部都是与接的重要措年季全国男子球甲?的大幕月日于福建晋江开启, 在国内各事于沉静的冬初春?的出色呈将除球迷和广大概育好者心中的孤独.同学 , 你看球比?你自己会打球?你自参加球比?二、生互 , 堂研究( 一) 提出 , 引依据球比, 每一球比束后, 得分高者. 假如得分同样, 必行加, 使得分生高低. 某次球中,? 火与汽要争一个出. 他与其余的比果都是 , 终究能出,? 就要看火和汽的比果, 比了就出. 下边有一个, 同学一下.( 二) 入知 , 解疑.背景某次球中, 火炬与月亮要争一个出, 火炬当前的是( 此中有以分之差于月亮), 后边要比(? 此中包含再与月亮比); 月亮当前的是, 后边要比 ..研究的()保证出 , 火炬在后边的比中起码要多少?()假如火炬在后边月亮比中起码月亮分, 那么它在后边的其余比中起码几就必定能出?()假如月亮在后边的比中( 包含火炬) ,? 那么火炬在后边的比中起码要几才能保证出?()假如火炬在后边的比中, 未能出 ,? 那么月亮在后边的比中的果怎样?.研究程与果()月亮在后边的比中至多, 所以整个比它至多.火炬在后边的比中, 保证火炬出, 需有 >, >,? 可知火炬在后边的比中起码 .()假如火炬在后边月亮比中起码月亮分, 那么火炬当前的是, 后边要比 ; 月亮当前的,? 后边要比; 月亮在后边的比中至多, 所以整个竞赛它至多胜场.设火炬队在后边的竞赛中胜场, 为保证火炬队出线, 需有 >. 则 >.? 所以火炬队在后边的竞赛中至少胜场就必定能出线.()假如月亮队在后边的竞赛中输赢, 则整个竞赛它的战绩为输赢.? 因为月亮队在后边胜了火炬队 , 则火炬队当前的战绩为输赢 , 后边还要竞赛场 , 这样设火炬队在后边场竞赛中要胜场才能保证出线, 则>, 解得 >.故火炬队在后边的竞赛中起码要胜场才能保证出线.()假如火炬队在后边的竞赛中输赢, 则它整个竞赛战绩为输赢,? 因为它未能出线, 则月亮队出线 .设月亮队在后边的竞赛中胜场, 为保证月亮队出线, 需要 >, 获得 >,? 所以当月亮队在后边场竞赛中战绩为全胜即战胜时, 火炬队不可以出线.但当月亮队在后场竞赛中输赢时, 火炬队也有可能不出线.? 即月亮队在后边的竞赛中的战绩为输赢 ( 不负于火炬队或在分之内负于火炬队).综上可得 : 假如火炬队在后边的竞赛中输赢, 未能出线 ,? 那么月亮队在后边的竞赛中的战果有三.种状况 : ①战胜 ; ②输赢 , 但不负于火炬队; ③输赢 ,? 有一场竞赛负于火炬队, 但要控制比分在分之内.想想依据上边问题情境, 假如火炬队在后边的竞赛中胜场,? 那么什么状况下它必定能出线?设月亮队在后边的竞赛中胜了场, 则 <, 解得 <, 所以为保证火炬队出线, 月亮队在后边场竞赛中只能胜场或场或场或场.本章小节例题解说研究活动（一）一台装载机每小时可装载石料吨 . 一堆石料的质量在吨至 ?吨之间 , 那么这台装载机大概要用多长时间才能将这堆石料装完 ?剖析 : 装载机每小时可装吨 , 而石料的质量多于吨而少于吨 ,? 则装载的时间在 1800 到2200 之间 , 故5050可设小时才能把石料装完, 则1800 << 2200 或 << 50 50解得 <<即装载石料的时间在～小时之间.研究活动（二）大、小盒子共装球个 , 每个大盒装 , 小盒装个 , 恰巧装完 , 盒子个数大于 , 问 : 大小盒子各多少个 ?剖析 : 问题中有两个未知量 , 只有一个等量关系 , 此外还有一个附带条件:设大、小盒分别有个、个12x 5 y 99, 依据题意得 :y 10x 由①知为奇数 ,且 99 5 y 5 y 3 ③12 12∵为自然数∴5y3为整数 , 经过试验可适当时 ,但与>矛盾,故舍去 ,当时,即x 2 12y 15作业：教材页、。