下载文档原格式
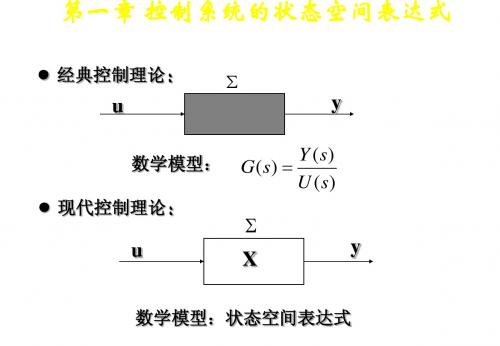
Chapter1控制系统的状态空间模型1.1 状态空间模型在经典控制理论中，采用n 阶微分方程作为对控制系统输入量)(t u 和输出量)(t y 之间的时域描述，或者在零初始条件下，对n 阶微分方程进行Laplace 变换，得到传递函数作为对控制系统的频域描述，“传递函数”建立了系统输入量)]([)(t u L s U =和输出量)]([)(t y L s Y =之间的关系。
传递函数只能描述系统的外部特性，不能完全反映系统内部的动态特征，并且由于只考虑零初始条件，难以反映系统非零初始条件对系统的影响。
现代控制理论是建立在“状态空间”基础上的控制系统分析和设计理论，它用“状态变量”来刻画系统的内部特征，用“一阶微分方程组”来描述系统的动态特性。
系统的状态空间模型描述了系统输入、输出与内部状态之间的关系，揭示了系统内部状态的运动规律，反映了控制系统动态特性的全部信息。
1.1.1 状态空间模型的表示法例1-1（6P 例1.1.1） 如下面RLC （电路）系统。
试以电压u 为输入，以电容上的电压C u 为输出变量，列写其状态空间表达式。
例1-1图 RLC 电路图解：由电路理论可知，他们满足如下关系⎪⎩⎪⎨⎧==++)(d )(d )()()(d )(d t i t t u C t u t u t Ri t t i L C C 经典控制理论：消去变量)(t i ，得到关于)(t u C 的2=n 阶微分方程：)(1)(1d )(d d )(d 22t u LCt u LC t t u L R t t u C C C =++ 对上述方程进行Laplace 变换：)()()2(20202s U s U s s C ωωζ=++得到传递函数：202202)(ωζω++=s s s G ，LC10=ω，L R 2=ζ 现代控制理论：选择⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛)()(21t u t i x x C 流过电容的电流)(t i 和电容上的电压)(t u C 作为2个状态变量，2=n （2个储能元件）；1个输入为)(t u ，1=m ；1个输出C u y =，1=r 。
状态方程的参数简介状态方程是描述动态系统行为的数学模型，它通过表示系统的状态和状态变化的方程来描述系统的演化规律。
状态方程的参数是指在状态方程中出现的变量和常数。
这些参数决定了系统的特性和行为，对于系统的分析和控制至关重要。
在本文中，我们将介绍状态方程的基本概念和常见形式，然后详细讨论状态方程的参数，包括变量和常数的定义、物理意义、取值范围以及对系统行为的影响。
状态方程的基本概念状态方程描述了系统的状态随时间的演化规律。
一般来说，状态方程可以写成如下形式：dx/dt = f(x, u, t)其中，x是系统的状态向量，u是系统的输入向量，t是时间，f是状态方程的右侧函数。
状态方程可以是线性或非线性的，具体形式取决于系统的性质和特点。
状态方程的参数包括状态向量x中的变量和常数，以及右侧函数f中的变量和常数。
下面我们将分别讨论这些参数的定义和物理意义。
状态向量的参数状态向量x是描述系统状态的一组变量。
它的具体定义和物理意义取决于系统的性质和特点。
下面是一些常见的状态向量及其参数的例子：•位置向量：描述物体在空间中的位置，参数包括物体在三个坐标轴上的位置变量（例如x、y、z）。
•速度向量：描述物体在空间中的速度，参数包括物体在三个坐标轴上的速度变量（例如v_x、v_y、v_z）。
•电路变量：描述电路中的电流和电压，参数包括电流和电压变量（例如i、v）。
状态向量的参数在状态方程中起到了关键的作用。
它们决定了系统的状态空间的维度和范围，以及状态变化的规律。
不同的参数可以对系统的行为产生不同的影响。
右侧函数的参数右侧函数f描述了状态向量x随时间的变化规律。
它的具体定义和物理意义也取决于系统的性质和特点。
下面是一些常见的右侧函数及其参数的例子：•线性函数：描述线性系统的状态变化规律，参数包括状态向量x、输入向量u和常数矩阵。
•非线性函数：描述非线性系统的状态变化规律，参数包括状态向量x、输入向量u和非线性函数。
第3章 开关变换器的状态空间平均建模开关变换器是通过调整开关元件的工作状态实现开关变换器输出电压的调整，在一个开关周期内，开关变换器是一个周期性时变电路，但在每一个开关工作状态，开关变换器又可以看作是一个线性电路。
因此，不能用常规的线性电路理论对开关变换器进行分析，而必须研究适用于开关变换器的建模分析方法。
3.1 CCM 开关变换器的状态空间平均模型3.1.1 CCM 开关变换器的状态空间方程及其近似解对于在开关周期T 内有两个开关工作状态的开关变换器，即开关变换器工作在CCM 模式，可以分别写出它在每一个开关工作状态的状态方程，并进行求解。
工作状态1：在一个开关周期的[0，DT ]时间段，开关变换器的状态方程为：d ()()()d t t t t=+11x A x B u(3.1a)工作状态2：在一个开关周期的[DT ，T ]时间段，开关变换器的状态方程为：d ()()()d t t t t=+22x A x B u(3.1b)其中：x (t )是状态向量；u (t )是输入向量；A 1、A 2、B 1、B 2分别是工作状态1和工作状态2对应的状态矩阵和输入矩阵。
（I ）开关工作状态1对应的状态方程的解为()()0d tte t t e ττ⎰111A A u x =x()+B(3.2)当开关变换器的开关频率(f s =1/T )远大于状态方程的特征频率f 0，即f s >> f 0时，存在下述线性近似关系DT DT e +≈11A I A(3.3)将式(3.3)代入式(3.2)，可得00()()0()d 0d DTDTDT DTet DT et eττττ+=+⎰⎰111A A A 111I A B u x()=x()+B u x() (3.4a)当开关变换器的输入向量u (t )在一个开关周期内是常数，或相对于开关频率是慢变化量时，可以用u (t )在一个开关周期内的平均值u 等效，于是，由式(3.4a)可得22120DTDT D T DT e++1A 111A x()=x()B u B u(3.4b)对于f s >> f 0，可以忽略式(3.4b)中的T 2项，从而得到下述线性近似关系0DT DT DT e ≈+11A u x()x()B(3.4c)（II ）开关工作状态2对应的状态方程的解为()()()d tDTt DT et t eDT ττ-⎰22A 2A u x =x()+B (3.5)同理，由式(3.5)可得： ()00T T TTTD D D D D D T D T T e e DT eeDT e''''+'=+11222A A 22A A A 22uu u ux()=B B x()+x()+B B (3.6)其中)(T D D T DT DT e ''=+2A 121u u A B I B(3.7)忽略式(3.7)中的T 2项，可得)(T D D T DT DT DT e ''≈=+2A 1211u u uA B I B B (3.8)将式(3.8)代入式(3.6)，得)()0(T D D T T e D D +'+'12A A 12u x()=x()+B B(3.9)式(3.9)对应的状态方程为：)d d ()(D D D tt t D ''++1212A A u x()=x()+B B(3.10)其中t x()为开关变换器在一个开关周期内状态向量的平均值，式(3.10)即为描述CCM 开关变换器在一个开关周期内的状态空间平均方程。
LPV模型的非线性PID控制算法黄江茵【摘要】以LPV模型为被控对象,提出一种适合动态系统、整定简便的非线性PID 控制算法.针对LPV模型时变非线性运行特性,引入工作点变量,采用传统Ziegler-Nichols法整定被控对象在工作点处的局部PID控制参数,通过高斯插值使控制参数在系统操作轨迹上的平滑过渡,有效避免控制参数突变对系统的冲击以及被控模型改变引起的误差,实现了对被控非线性对象的高效稳定控制.【期刊名称】《厦门理工学院学报》【年(卷),期】2015(023)003【总页数】5页(P36-40)【关键词】LPV模型;非线性PID控制;高斯插值【作者】黄江茵【作者单位】厦门理工学院电气工程与自动化学院,福建厦门361024【正文语种】中文【中图分类】TP273.2尽管近年来，如模型预测控制等先进控制算法不断推出，但PID控制器以其结构简单，对模型误差具有鲁棒性及易于操作等优点，仍然被广泛应用于冶金、化工等工业过程控制中.随着对非线性系统控制精度要求的不断提高，PID参数的智能整定算法［1-2］、非线性PID调节器设计［3］等改进的PID算法也越来越受到关注.变参数线性（linear parameter varying，LPV）模型是近10年来学术界广泛关注的非线性模型结构之一，虽然其辨识方法层出不穷［4］，但针对该模型的控制算法却少有人涉猎.原因在于LPV模型的非线性时变特性，大大增加了先进控制算法中预估系统输出以及控制约束方程的寻优难度，甚至无法获得局部收敛的最优解.针对此问题，本文利用PID控制器鲁棒性强、参数个数少、整定方便等显著优点，首先针对系统运行的若干个稳态阶段整定局部PID参数，随后引入LPV模型辨识中常见的“工作点变量”概念，以其为自变量构建高斯权重函数对局部参数进行插值，使控制参数在被控对象的整个操作轨迹上实现动态平滑过渡，获得较好的控制效果.目前为止，学术界已讨论过各种类型的非线性PID控制器.根据控制原理，这些非线性PID控制器可以分为两类：一类是直接控制量（direct-action）型，一类是增益调整（gain-scheduling）型［5］.数学表达形式分别为：直接控制量型：增益调整型：其中：u，e（t）分别为控制量输入与控制响应的误差；x，θ分别为非线性函数的自变量与参数向量；下标P，I，D分别对应比例、积分、微分含义.由上述两类非线性PID控制器的表达式中可以看出，直接控制量型控制器是对控制分量进行非线性设计，而增益调整型控制器则是对增益参数的非线性进行规划调整.文献［5］采用的是直接控制量型PID控制器，采用3个相同的样条函数对误差e（t）进行非线性处理，处理后的信号再分别进行比例、积分和微分计算.文献［6］则采用了增益调整型PI控制器，在KP，KI前增加了“前项增益切换机制”，实现KP，KI的简单线性过渡.鉴于直接控制量型PID控制器中，对积分、微分控制分量的非线性特性先验知识不够充分［5］，本文采用的是增益调整型结构，直接针对KP，KI，KD设计非线性函数，该非线性PID控制器的结构如图1所示.随着近几年来工业系统自动控制要求的不断提高，以及过程设计、分析、全过程运行最优化等命题的提出，变参数模型越来越得到学术界和工业界的重视.其中，最受瞩目之一的便是LPV模型［7］. LPV模型的主导思想是用一个包含时变参数的整体模型来描述非线性系统.该时变参数可以是系统工作点或者其他外部变量的函数.LPV模型的状态空间形式可表示为式（1）中：w（t）就是所谓的工作点变量；状态空间矩阵A，B，C，D都是w （t）的函数.LPV模型的控制问题一直是学术界公认的难点.众多先进的控制算法都对LPV模型束手无策.以模型预测控制算法为例，首先LPV模型是时变模型，难以预测系统在未来一定时间内的输出；其次预测控制算法中的分层优化需以被控对象模型作为约束方程［8］，而求解动态非线性约束问题一直是难以逾越的数学难题，极易因为初值设定、下降方向选择偏差而造成无法收敛，也很难获得局部最优解.考虑到PID控制器的鲁棒性，以及其待估参数少、整定方便等显著优点，采用非线性PID 控制器对LPV模型进行控制，则能够避开上述复杂的非线性优化命题，同时获得较好的控制效果.大多数非线性工业系统的运行轨迹，并不是杂乱无章的.大多数的工业过程，其运行轨迹都是由若干个“稳态阶段”以及过渡过程构成.在稳态阶段，系统运行在相对平稳的状态，主要操作变量和被控变量，包括工作点变量w（t）均处于相对恒定状态；在过渡过程，各变量也出现相应的过渡变化.由上述特点可推知，针对LPV模型的控制器，在稳态阶段可以采用传统线性控制器进行控制；而在过渡阶段，则需要采用某种算法重新设计控制参数，以适应LPV模型的动态特性.本文采用增益调整型PID进行控制，需要解决的核心问题在于如何设计KP（x，θP），KI（x，θP），KD（x，θP），使其能根据当前系统运行状态进行自动调整，同时又能满足超调小、响应迅速、无稳态误差这3点控制要求.根据上述分析和要求，可先整定稳态工作点处的局部PID控制参数，后采用高斯函数对这些局部参数进行插值获得最终非线性PID参数.具体步骤如下：步骤1：在系统的各个稳态阶段，采用传统线性PID控制器整定方法（如Ziegler-Nichols法、衰减曲线法、临界比例度法等），获取局部控制参数.假设被控对象有n个稳态，对应的工作点变量值为wi，（i=1，2，…，n），整定后的控制参数为KPi，KIi，KDi（i=1，2，…，n）步骤2：构建高斯函数计算局部控制参数权重，插值获得基于LPV模型的非线性PID控制器输出.式（2）中：KP，KI，KD分别为非线性PID控制器的比例、积分、微分参数；αi （w（t））是以w（t）为自变量的归一化高斯函数，作为稳态线性PID参数的权重.归一化的目的在于使各局部参数的权重值之和为1.参数σi（i=1，2，n）称为分离（或宽度）系数，可以简单地根据高斯函数的图象和权重的物理意义，将其设定为相邻工作点之间的间隔的三分之一，也可以通过极小化输出误差来估计.以最速下降法为例，损失函数极小化问题如式（5）所示：式（5）中：r（t）为设定值；y（t）为闭环系统输出；u（t）为非线性PID控制器输出；G（s，w）为被控对象LPV模型；N为样本空间容量.采用最速下降法进行寻优的流程如下：步骤1：初始化σi（i=1，2，…，n），记为σi（1）.根据高斯函数图像特征以及LPV模型权重函数的物理意义，将其设定为相邻工作点间隔的三分之一.定义误差阈值ε＞0以及迭代次数k=1.步骤2：沿被控对象的操作轨迹，采用上述非线性PID控制算法进行控制，采集数据集：Zn=｛y（t），r（t），w（t）｝，t=1，2，…，N；步骤3：计算负梯度向量d（k）=-∇f（σ（k）），其中步骤：4：若则停止搜索；σ（k）即为待定参数值，将其设为高斯权重的分离系数；否则，计算中的λ 值，其中，σ（k）=步骤5：计算σ（k+1）=σ（k）+λk×d（k），k=k+1；跳转步骤3.图2为当系统有4个工作点w1=20，w2=40，w3= 60，w4=80时对应的高斯权重值.从图2中可以看出，各个权重值均在接近它对应的工作点时达到最大值1，而随着远离对应工作点，平滑过渡到最小值0.任一时刻，各个权重值之和均为1.值得注意的是，由于高斯函数图象的对称性，采用高斯权重要求系统的工作点等间隔分布.如果系统的工作点之间的间隔不同，则可将高斯函数写成分段函数，间断点为各个工作点，并令各个分段高斯函数的分离系数不同.各局部PID参数的权重，不一定通过高斯函数获得，也可以构造线性函数、样条函数、多项式函数等计算.本文采用高斯函数的理由是，它的函数值比线性函数更加平滑，可以避免由于控制参数突变对系统造成的冲击，减小超调；相较于样条函数和多项式函数，它可以通过归一化保证各权重值之和在任意时刻均为1，符合插值的物理意义，而样条函数和多项式函数则有较多待估参数，难以同时保证误差极小化和函数值之和为1，也无法保证函数值介于［0，1］之间.以典型的MIMO二阶LPV模型为控制对象进行非线性PID控制仿真.仿真时间为13 s，采样周期1 ms，共采集13 000个数据.假设系统模型如下：式（6）中：w（t）为工作点变量，假定系统有2个局部稳态，对应的w（t）值分别为w1=1，w2=3.系统的整个运行轨迹上，w（t）的变化规律为：首先在2个稳态阶段，分别采用传统Ziegler-Nichols法整定局部线性PID参数，并进行微调以提高控制效果.两组局部KP，KI，KD如下：根据本文第2部分提出的方法，构建高斯权重函数并实时插值计算非线性PID控制器的参数以及输出.由于只有2个工作点，高斯权重中的分离系数σ未进行优化，而是定为工作点距离的1/3，即σ=（3-1）/3.为验证所提算法的抗干扰能力，t=6～10 s阶段，在仿真系统的输入端叠加了大小为0.5w2（t）的扰动信号.仿真控制结果如图3所示.从图3可以看出，虽然被控对象为时变非线性过程，但非线性PID控制依然可以实现在整个运行轨迹上的较好控制效果.若采用线性PID进行控制，由于恒定的控制参数无法适应时变的动态LPV模型，系统出现了较大的超调，而非线性PID控制器则可以同时保证较小的超调、较短的调节时间和较小的稳态误差.加入扰动信号后，线性PID控制下的系统出现了较大幅度的波动，而非线性PID控制器则能有效地减小系统波动并使输出较快稳定到设定值.LPV模型是用于辨识工业系统的常用非线性时变模型，针对LPV模型的先进控制算法常因为难以求解非线性动态约束的优化命题而失败.本文针对LPV模型的动态特性，提出了一种增量调整型非线性PID控制算法，首先在系统稳态工作点上整定局部线性的PID参数，然后以工作点变量为自变量构建高斯函数权重，插值获得非线性PID的整体控制参数.该方法既避免了复杂的非线性寻优计算，又能够根据系统运行的动态特征实时更新参数，符合LPV模型以及大多数工业非线性对象的控制需求.仿真结果表明该方法与传统线性PID控制相比，能够在整个运行轨迹上获得良好的控制效果，超调小，抗干扰能力强，响应迅速且无稳态误差.【相关文献】［1］金钊，刘丽华.PID参数模糊自整定控制在液位控制系统中的应用［J］.北京信息科技大学学报：自然科学版，2014，29（4）：86-89.［2］于洪国，王平.一种改进的最优PID参数自整定控制方法［J］.现代电子技术，2010，19（1）：162-164.［3］曾喆昭，肖雅芬，蒋杰，等.高斯基神经网络的非线性PID控制方法［J］.计算机工程与应用，2013，49（9）：255-258.［4］黄江茵.带约束多项式权重LPV模型辨识算法研究［J］.厦门理工学院学报，2014，22（3）：45-50.［5］胡包钢.非线性PID控制器研究-比例分量的非线性方法［J］.自动化学报，2006，32（2）：219-227.［6］邵辉，胡伟石，罗继亮.基于LPV模型的鲁棒PI控制方法［J］.北京工业大学学报，2012，38（12）：1 761-1 765.［7］LAURAIN V，GILSON M，T’OTH R，et al.Refined instrumental variable methods for identification of LPV Box-Jenkins models［J］.Automatica，2010，46（6）：959-967. ［8］陈虹.模型预测控制［M］.北京：科学出版社，2013：14-30.。
