(完整)社会统计学公式总结及要点,推荐文档

统计学原理知识点及公式第一章统计总论•1.统计一词的三种含义•2.统计学的研究对象及特点•3.统计学的研究方法•4.统计学的几个基本概念：总体与总体单位、标志与标志表现、变异与变量、统计指标的概念、特点及分类。

•5.国家统计兼有的职能第二章统计调查•1.统计调查的概念和基本要求•2.统计调查的种类•3.统计调查方案的构成内容•4.统计调查方法：普查、抽样调查、重点调查、典型调查•5.调查误差的种类第三章统计整理•1.统计整理的概念和方法•2.统计分组的概念、种类•3.统计分组的关键•4.统计分组的方法：品质分组方法、变量分组的方法•5.分配数列的概念、构成及编制方法变量数列的编制基本步骤为：第一步：将原始资料按数值大小依次排列。

第二步：确定变量的类型和分组方法（单项式分组或组距分组）。

第三步：确定组数和组距。

当组数确定后，组距可计算得到：组距= 全距÷组数全距= 最大变量值－最小变量值。

第四步：确定组限。

（第一组的下限要小于或等于最小变量值，最后一组的上限要大于最大变量值。

）第五步：汇总出各组的单位数（注意：不同方法确定的组限在汇总单位数时的区别），计算频率，并编制统计表。

间断式确定组限：汇总各组单位数时，按照“上下限均包括在本组内”的原则汇总。

重叠式确定组限：汇总各组单位数时，按照“上组限不在内”的原则汇总。

因为有了“上组限不在内”的原则，实际工作中，对于离散型变量也经常采用重叠式确定组限的方法。

•6.统计表的结构和种类第四章综合指标•1.总量指标的概念、种类和计量单位•2.相对指标的概念、指标数值的表现形式、相对指标的种类。

相对指标包括：结构相对指标、比例相对指标比较相对指标、强度相对指标动态相对指标、计划完成程度相对指标●3.平均指标的概念、作用和种类。

算术平均数、调和平均数、众数、中位数●4.变异指标的概念、作用和种类。

●全距、平均差、标准差、变异系数第五章 抽样估计•1.抽样推断的概念、特点、和内容。

公式一1. 众数【MODE 】（1） 未分组数据或单变量值分组数据众数的计算未分组数据或单变量值分组数据的众数就是出现次数最多的变量值。

（2） 组距分组数据众数的计算对于组距分组数据，先找出出现次数最多的变量值所在组，即为众数所在组，再根据下面的公式计算计算众数的近似值。

下限公式： 1012M =L++i ∆⨯∆∆ 式中：0M 表示众数；L 表示众数的下线；1∆表示众数组次数与上一组次数之差；2∆表示众数组次数与下一组次数之差；i 表示众数组的组距。

上限公式：2012M =U-+i ∆⨯∆∆ 式中：U 表示众数组的上限。

2．中位数【MEDIAN 】（1）未分组数据中中位数的计算根据未分组数据计算中位数时，要先对数据进行排序，然后确定中位数的位置。

设一组数据按从小到大排序后为12N X X X ，，…，，中位数e M ，为则有：e N+M =X1（）2当N 为奇数e N N +1221M =X +X 2⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭⎧⎫⎪⎪⎨⎬⎪⎪⎩⎭ 当N 为偶数（2）分组数据中位数的计算分组数据中位数的计算时，要先根据公式N / 2 确定中位数的位置，并确定中位数所在的组，然后采用下面的公式计算中位数的近似值：N=1m-1e m-S 2M =L+ii fd f ⨯∑式中：e M 表示中位数；L 表示中位数所在组的下限；m-1S 表示中位数所在组以下各组的累计次数；m f 表示中位数所在组的次数；d 表示中位数所在组的组距。

3．均值的计算【A VERAGE 】（1）未经分组均值的计算未经分组数据均值的计算公式为： 112n ++==nii x x x x x n n=∑…（2）分组数据均值计算分组数据均值的计算公式为： 11221121+++==+ki ik k i k kii x f x fx f x fx f f f f==+∑∑+4．几何平均数【GEOMEAN 】几何平均数是N 个变量值乘积的N 次方根，计算公式为：式中：G 表示几何平均数；∏表示连乘符号。

统计学公式总结统计学是一门关于收集、分析、解释和表达数据的科学。

它通过具体的数学模型和公式来描述和理解数据中的规律和关系。

在统计学中，有许多重要的公式被广泛应用于各种数据处理和分析的情况。

本文将会总结一些常见和重要的统计学公式。

1. 均数公式：均数是一组数据的平均值，用于反映一组数据的中心位置。

计算均数的公式是：mean = sum(data) / n其中，data表示数据集，n表示数据的个数，sum表示求和。

2. 中位数公式：中位数是将一组数据按照大小排列后，位于中间位置的数值。

计算中位数的公式有两种情况：- 当数据集的个数n为奇数时，中位数的公式是：median = data[(n+1)/2]- 当数据集的个数n为偶数时，中位数的公式是：median = (data[n/2] + data[(n/2)+1]) / 23. 众数公式：众数指一组数据中出现频率最高的数值。

计算众数的公式是：mode = value with maximum frequency4. 方差公式：方差是一组数据与其均值之间差异的平方的平均值。

方差可以用于衡量数据的离散程度，公式如下：variance = sum((data - mean)^2) / n5. 标准差公式：标准差是方差的正平方根，用于衡量数据集的离散程度。

标准差的公式是：standard deviation = sqrt(variance)6. 协方差公式：协方差用于衡量两个变量之间的相关性。

协方差的公式为：covariance = sum((X - mean_X) * (Y - mean_Y)) / n其中，X和Y表示两个变量，mean_X和mean_Y表示X和Y的均值，n表示变量的个数。

7. 相关系数公式：相关系数用于衡量两个变量之间的线性相关性，其取值范围为-1到1。

相关系数的公式是：correlation = covariance / (std_X * std_Y)其中，std_X和std_Y表示X和Y的标准差。

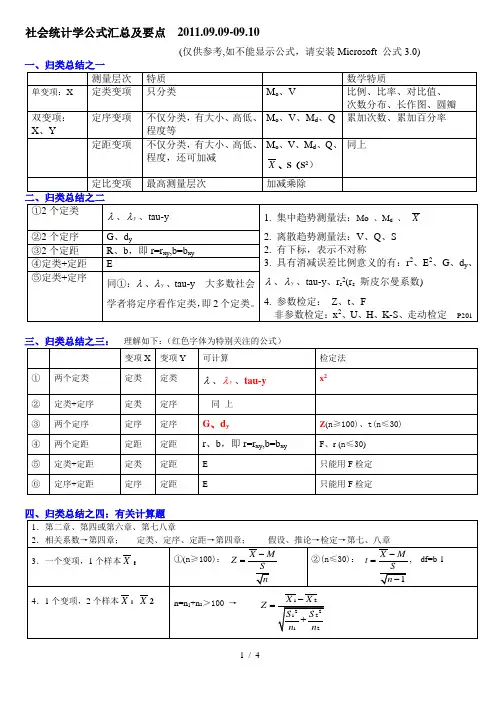
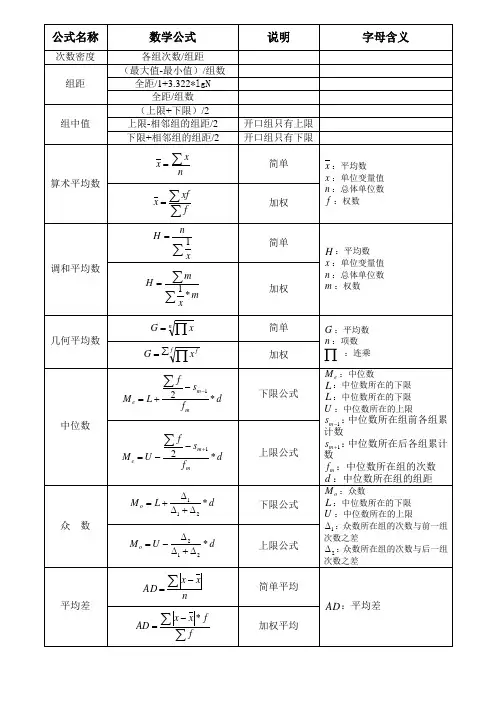
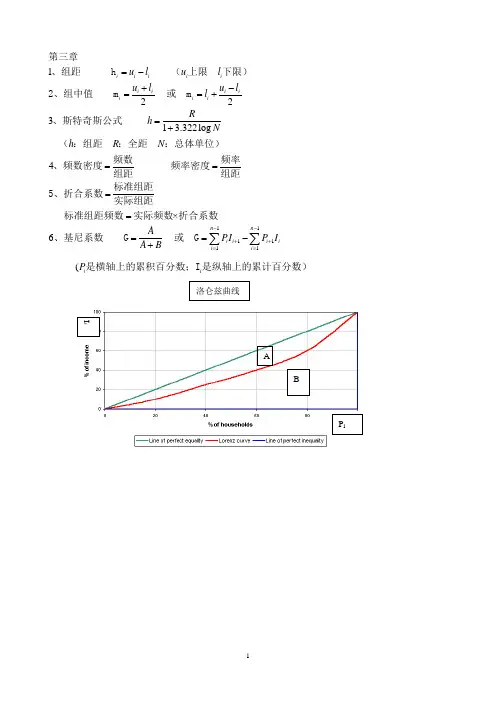
12231 3.322log 4×6i i i i i i i i i i i i u l u l u l u ll Rh N h R N AA B =-+-==+=+=====+第三章、组距 h （上限 下限）2、组中值 m 或 m 、斯特奇斯公式 （：组距 ：全距 ：总体单位）频数频率、频数密度 频率密度组距组距标准组距5、折合系数实际组距标准组距频数实际频数折合系数、基尼系数 G 111111n n i i i ii i PI P I --++===-∑∑ 或 G(i i P 是横轴上的累积百分数；I 是纵轴上的累计百分数）洛仑兹曲线P iI iAB1(2))(1)1221222d d X X X N fXX fN NN NN F L ==++-=+∑∑∑第四章1、算术平均数（）（）未分组资料 分组资料 注：对于单项数列分组，X即为变量值，若为组距式分组，则X为组中值 f:各组频数2、中位数（M 未分组资料 若N为奇数，则取第位上的变量值为中位数，若为偶数，则取第 位和第位上的两个变量值的平均数作为中位数（）分组资料 M 112h h L : 2m m d m m m m m N F U f f f F F N---⨯=-⨯或 M 中位数所在组的下限： 中位数所在组的频数： 小于中位数所在组的各组频数之和（向上累计） h ： 中位数所在组的组距 U: 中位数所在组的上限： 包括中位数所在组的各组频数之和（向上累计） 注： 中位数所在组由确定11111111133333334h :h 34h :N F l f F l f NF l f F l -=+⨯-=+⨯3、四分位数（1）第一四分位数 Q ：小于第一四分位数所在组的各组累计频数（向上累计） 第一四分位数所在组的下限 ：第一四分位数所在组的组距 ：第一四分位数所在组的组距（2）第三四分位数 Q ：小于第三四分位数所在组的各组累计频数（向上累计） 第三四分位数所在组的3311212h 1h :h 5o o o oo o f L L ∆=+⨯∆+∆∆∆下限 ：第三四分位数所在组的组距 ：第三四分位数所在组的组距4、众数（M ）（）未分组资料 先将所有数据顺序排列，观察某些变量值出现的次数最多，这些变量值就 是众数（2）分组资料 M 众数所在组的下限：众数所在组频数与前一组频数之差 ：众数所在组频数与后一组频数之差 ：众数所在组的组距、几何平均数11lg lg anti(lg )(2)1lg lg anti(lg )g g g g g gg g g X Nf X NX ========∑∑（M ）（）简单几何平均数 M 或 M M M 加权几何平均数M 或 M M M 注：若为组距式分组，则为组中值3112316)(1)111111...(2):312=23h h N h d o g h N Q Q NX X X X XNNf XX f X X -==++++==-≥≥-⋅∑∑、调和平均数（M 简单调和平均数（未分组） M 加权调和平均数（分组）M 注：若为组距式分组，为组中值 各组频数7、各种平均数的关系2M M M M 第五章、全距 R=X X 、四分位差 Q D、平均差=2=::X X Nf X XfX f X f -⋅-⋅∑∑（1）未分组资料 A D （）分组资料 A D 注：若为组距式分组，为组中值 各组频数4、标准差（S）（1）未分组资料(2)分组资料 注：若为组距式分组，为组中值 各组X X S-频数5、标准分 Z=社会统计学复习整理一、变量的测量层次61(2)37=1:83(o o oR R M M M o d o R X X SXN f f NNf X M X M X M S Sαα⋅⋅=-⋅=----==A D 、变异系数（）全距系数 V =A D平均差系数 V =（）标准差系数 V 、异众比率（非众数的频数与总体单位数的比值） V R 众数的频数、偏态系数())偏态=二、判断变量层次的技巧1.首先所有的变量都是定类变量。

公式一1. 众数【MODE 】（1） 未分组数据或单变量值分组数据众数的计算未分组数据或单变量值分组数据的众数就是出现次数最多的变量值。

（2） 组距分组数据众数的计算对于组距分组数据，先找出出现次数最多的变量值所在组，即为众数所在组，再根据下面的公式计算计算众数的近似值。

下限公式： 1012M =L++i ∆⨯∆∆ 式中：0M 表示众数；L 表示众数的下线；1∆表示众数组次数与上一组次数之差；2∆表示众数组次数与下一组次数之差；i 表示众数组的组距。

上限公式：2012M =U-+i ∆⨯∆∆ 式中：U 表示众数组的上限。

2．中位数【MEDIAN 】（1）未分组数据中中位数的计算根据未分组数据计算中位数时，要先对数据进行排序，然后确定中位数的位置。

设一组数据按从小到大排序后为12N X X X ，，…，，中位数e M ，为则有：e N+M =X1（）2当N 为奇数e N N +1221M =X +X 2⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭⎧⎫⎪⎪⎨⎬⎪⎪⎩⎭ 当N 为偶数（2）分组数据中位数的计算分组数据中位数的计算时，要先根据公式N / 2 确定中位数的位置，并确定中位数所在的组，然后采用下面的公式计算中位数的近似值：N=1m-1e m-S 2M =L+ii fd f ⨯∑式中：e M 表示中位数；L 表示中位数所在组的下限；m-1S 表示中位数所在组以下各组的累计次数；m f 表示中位数所在组的次数；d 表示中位数所在组的组距。

3．均值的计算【A VERAGE 】（1）未经分组均值的计算未经分组数据均值的计算公式为： 112n ++==nii x x x x x n n=∑…（2）分组数据均值计算分组数据均值的计算公式为： 11221121+++==+ki ik k i k kii x f x f x f x f x f f f f==+∑∑+4．几何平均数【GEOMEAN 】几何平均数是N 个变量值乘积的N 次方根，计算公式为：式中：G 表示几何平均数；∏表示连乘符号。

统计学常用公式汇总优秀版《统计学原理》常用公式汇总第三章统计整理a) 组距＝上限－下限 b) 组中值＝（上限+下限）÷2c) 缺下限开口组组中值＝上限－1/2邻组组距d) 缺上限开口组组中值＝下限+1/2邻组组距第四章综合指标i. 相对指标1.结构相对指标＝各组（或部分）总量/总体总量2.比例相对指标＝总体中某一部分数值/总体中另一部分数值3.比较相对指标＝甲单位某指标值/乙单位同类指标值4.强度相对指标＝某种现象总量指标/另一个有联系而性质不同的现象总量指标5.计划完成程度相对指标＝实际数/计划数＝实际完成程度（%）/计划规定的完成程度（%）ii.平均指标1.简单算术平均数：或iii.变异指标1.全距＝最大标志值－最小标志值2.标准差: 简单σ= ；加权σ=3.标准差系数:第五章抽样估计1.平均误差：重复抽样：不重复抽样：2.抽样极限误差3.重复抽样条件下：平均数抽样时必要的样本数目成数抽样时必要的样本数目4.不重复抽样条件下：平均数抽样时必要的样本数目第七章相关分析1.相关系数2.配合回归方程ｙ＝ａ＋ｂｘ3.估计标准误：第八章指数分数一、综合指数的计算与分析(1)数量指标指数此公式的计算结果说明复杂现象总体数量指标综合变动的方向和程度。

( - )此差额说明由于数量指标的变动对价值量指标影响的绝对额。

(2)质量指标指数此公式的计算结果说明复杂现象总体质量指标综合变动的方向和程度。

（ -）此差额说明由于质量指标的变动对价值量指标影响的绝对额。

加权算术平均数指数=加权调和平均数指数=(3)复杂现象总体总量指标变动的因素分析相对数变动分析：= ×绝对值变动分析：- = ( - )×（ -）第九章动态数列分析一、平均发展水平的计算方法：(1)由总量指标动态数列计算序时平均数①由时期数列计算②由时点数列计算在间断时点数列的条件下计算：a.若间断的间隔相等，则采用“首末折半法”计算。

社会统计学(Social Statistics)科学只有当它利用了数学的时候，它才达到了完善的程度。

——马克思对于追求效率的公民而言，统计思维总有一天会和读写能力一样必要。

——H.G.Wells教材及参考书目社会统计学，张彦，高等教育出版社，2005社会统计学，张彦，南京大学出版社，1997社会统计学（第八版），布莱洛克，社会科学文献出版社社会统计学（重排本），卢淑华，北京大学出版社，2002社会研究的统计分析，李沛良，社会科学文献出版社17世纪以前，社会统计主要局限于对事物进行原始的调查登记和简单的计算汇总。

如大禹时的九州表，明初的黄册和鱼鳞册；古埃及、古希腊、古罗马在公元前400年就建立的出生、死亡登记制度。

17世纪后，产生了以工业、农业、贸易、交通等方面统计为主的社会经济统计。

国势学派政治算术学派数理统计学派1.国势学派代表人物是康令（1606~1681）和阿亨瓦尔（1719~1772）。

1749年，阿亨瓦尔根据拉丁文“Status”、意大利文Stato 和Statista及德文Statisti等字根创造出“Statistik”这个新词，原意指“国家显著事项的比较和记述”。

国势学派可谓“有名无实”的学派：只用文字记述，不用数字计量。

它又称记述学派和历史学派。

2. 政治算术学派格朗特1662年在其《自然和社会观察》一书中，从宗教管理、商业、气候、疾病等方面，对当时伦敦人口的出生率、死亡率和性比例等方面进行了综合的统计分析。

威廉·配第1667年在其《政治算术》一书中，运用有关人口、土地税收和国家收入等方面的数字资料，对英国、荷兰的经济实力进行比较，首创了一种数字对比分析的方法。

“即用数字、重量、尺度来表达自己想说的问题。

”与国势学派相对应，政治算术学派可谓“有实无名”的学派3.数理统计学派凯特勒（1796~1896）首先将概率论原理引入到社会现象的研究，在《社会物理学》，《道德统计》、《论人类》等书中，他认识到人类的社会活动服从于一定规律，并发现这种规律只有通过大量观察才能被人们所认识。

第一章数据与统计学数据分析所使用的方法大体上可分为描述统计和推论统计（推断统计），描述统计主要是利用图表形式对数据进行展示，或通过计算一些简单的统计量（诸如:比例、比率、平均数、标准差等）对数据进行分析。

推断统计主要研究如何根据样本信息来推断总体的特征，内容包括参数估计和假设检验两大类。

变量：是描述观察对象某种特征的概念，其特点是从一次观察到下一次观察可能会出现不同的结果（具有一个以上取值的概念）1、下列哪一个选项不是变量?( )A. 民族B. 智商C. 衣服的尺寸D. 女性答案：C2、下列变量属于数值型变量的是( )A. 工资收入B. 产品等级C. 学生对考试改革的态度D. 企业的类型答案：A解析：3、社会统计学的数据分析方法主要包括统计描述和( )A. 统计描述B. 统计推导C. 统计推论D. 统计分析答案：C4、能计算均值和标准差的必须是哪种变量( )A. 自变量B. 因变量C. 数值型变量D. 字符串型变量答案：C5、在SPSS中最多可以设置几个独立的缺失值?( )A. 3B. 4C. 5D. 8答案：A6、描述统计可以最恰当地表述为( )A.数据作概括性的表达B.对总体所作的结论C.测量操作的应用D.原始数据到标准分的转变答案：A解析：描述统计主要是利用图表形式对数据进行展示，或通过计算一些简单的统计量（诸如:比例、比率、平均数、标准差等）对数据进行分析。

第二章数据的描述性分析：图表展示1、欲以图形显示两变量X和Y的关系,最好创建( )。

A. 直方图B. 圆形图C. 柱形图D. 散点图答案：D第三章数据的描述性分析：概括性度量1、下列统计指标中,对极端值的变化最不敏感的是( )。

A. 众值B. 中位值C. 四分位差D. 均值答案：A2、经验法则表明,当一组数据正态分布时,在平均数加减1个标准差的范围之内大约有 ( )A. 50%的数据B. 68%的数据C. 95%的数据D. 99%的数据答案：B解析：根据标准得分可以判断一组数据中是否存在离群点。

公式一1. 众数【MODE 】（1） 未分组数据或单变量值分组数据众数的计算未分组数据或单变量值分组数据的众数就是出现次数最多的变量值。

（2） 组距分组数据众数的计算对于组距分组数据，先找出出现次数最多的变量值所在组，即为众数所在组，再根据下面的公式计算计算众数的近似值。

下限公式： 1012M =L++i ∆⨯∆∆ 式中：0M 表示众数；L 表示众数的下线；1∆表示众数组次数与上一组次数之差；2∆表示众数组次数与下一组次数之差；i 表示众数组的组距。

上限公式：2012M =U-+i ∆⨯∆∆ 式中：U 表示众数组的上限。

2．中位数【MEDIAN 】（1）未分组数据中中位数的计算根据未分组数据计算中位数时，要先对数据进行排序，然后确定中位数的位置。

设一组数据按从小到大排序后为12N X X X ，，…，，中位数e M ，为则有：e N+M =X1（）2当N 为奇数e N N +1221M =X +X 2⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭⎧⎫⎪⎪⎨⎬⎪⎪⎩⎭ 当N 为偶数（2）分组数据中位数的计算分组数据中位数的计算时，要先根据公式N / 2 确定中位数的位置，并确定中位数所在的组，然后采用下面的公式计算中位数的近似值：N=1m-1e m-S 2M =L+ii fd f ⨯∑式中：e M 表示中位数；L 表示中位数所在组的下限；m-1S 表示中位数所在组以下各组的累计次数；m f 表示中位数所在组的次数；d 表示中位数所在组的组距。

3．均值的计算【A VERAGE 】（1）未经分组均值的计算未经分组数据均值的计算公式为： 112n ++==nii x x x x x n n=∑…（2）分组数据均值计算分组数据均值的计算公式为： 11221121+++==+ki ik k i k kii x f x f x f x f x f f f f==+∑∑+4．几何平均数【GEOMEAN 】几何平均数是N 个变量值乘积的N 次方根，计算公式为：式中：G 表示几何平均数；∏表示连乘符号。

第7章住户活动统计
第一节住户活动及其统计内容
1、住户的概念
2、住户活动统计应该包括的内容
3、住户的分类
第二节居民收入统计
1、居民收入、居民消费、居民投资、居民财产的含义
2、居民总收入和居民可支配收入的概念
3、工资性收入、经营性收入、财产性收入、转移性收入
4、居民收入需要明确的两点
5、住户收入总量统计：
1）住户总收入：城镇住户总收入、农村住户总收入
2）住户可支配收入：城镇住户可支配收入、农村住户纯收入（可支配收入）、农村住户现金收入
6、居民收入水平及其变动统计：
1）总体人均收入
2）户人均收入
3）实际收入
7、居民收入结构统计：
第三节居民消费统计
1、居民消费含义
2、居民消费统计需注意的六点
3、居民消费总量及其水平统计：
1）住户主要消费品消费量和人均消费量：居民人均消费品消费量；户人均消费品消费量
2）居民消费支出总额与人均消费支出：人均年消费支出；户人均年消费支出4、居民消费倾向与消费结构统计：
1）居民消费倾向统计：居民平均消费倾向；居民边际消费倾向
2）居民消费结构统计：消费内容结构；消费方式结构；消费目的结构
5、恩格尔系数及其应用：恩格尔定律；恩格尔系数定义及计算公式
第四节居民收入、消费分布差异的统计与分析。

社会统计学公式汇总及要点2011.09.09-09.10(仅供参考,如不能显示公式，请安装Microsoft 公式3.0)一、归类总结之一测量层次特质数学特质单变项：X定类变项只分类M o、V比例、比率、对比值、次数分布、长作图、圆瓣双变项：X、Y 定序变项不仅分类，有大小、高低、程度等M o、V、M d、Q累加次数、累加百分率定距变项不仅分类，有大小、高低、程度，还可加减M o、V、M d、Q、、S（S2）X同上定比变项最高测量层次加减乘除二、归类总结之二①2个定类、、tau-y λyλ②2个定序G、d y③2个定距R、b，即r=r xy,b=b xy④定类+定距E⑤定类+定序同①：、、tau-y大多数社λyλ会学者将定序看作定类，即2个定类。

1. 集中趋势测量法：Mo 、M d、X2. 离散趋势测量法：V、Q、S2. 有下标，表示不对称3. 具有消减误差比例意义的有：r2、E2、G、d y、、、tau-y、r s2(r s斯皮尔曼λyλ系数)4. 参数检定：Z、t、F非参数检定：x2、U、H、K-S、走动检定P201三、归类总结之三：理解如下：（红色字体为特别关注的公式）变项X 变项Y可计算检定法①两个定类定类定类、、tau-yλyλx2②定类+定序定类定序同上③两个定序定序定序G、d y Z(n≥100)、t(n≤30)④两个定距定距定距r、b，即r=r xy,b=b xy F、r (n≤30)⑤定类+定距定类定距E只能用F检定⑥定序+定距定序定距E只能用F检定五、归类总结之五：有关消减误差比例1.有 消减误差比例意义，且 对称、G 、Q 拉系数、r s 2、r 2、r xy.12、、R y.122= R y.x1x22λ2．有 消减误差比例意义，且 不 对称d y 、、tau-y 、E 2、CR 2（特征值）y λ3.无 消减误差比例意义，且对称、V 系数、C 系数、tau-a 、tau-b 、tau-c 、Vs 、rϕ4.无 消减误差比例意义，且 不 对称b 、E六、其他细节1．显著度的表达①两端检定：； ②一端检定：； ③； ④F (df1,df2) ； ⑤x 2(df)1.96Z ≥ 1.65Z ≥(df)Z∂2. 有无自由度的表达G 、r 、F 、x 2 结果解释加上“其显著度水平达到或没有达到……水平”3. 有关r 净相关系数 （两个定距变项）r=r xy.1 —— 引入第三个变项时对X 、Y 变项产生共同影响。

統計學公式及重點整理第三章 機率論一、樣本空間與事件1. 機率:衡量事件發生之可能大小2. 實驗:蒐集資料的過程3. 隨機實驗:不能預知會發生何種結果的實驗方式4. 樣本點:每一個實驗的可能的結果,亦稱為出象5. 樣本空間:所有實驗可能產生之結果所成的集合,以大寫S 來表示6. 有限樣本空間:具有”有限”或”無限但可數”的樣本點之樣本空間7. 無限樣本空間:具有”無限且不可數”的樣本點之樣本空間8. 事件:樣本空間之子集合9. 不可能事件:事件為空集合,一般以∅表示10. 簡單事件:只包含一個樣本點的事件11. 複合事件:包含一個以上樣本點的事件12. 事件之集合運算事件的交集:B A事件的聯集:B A13. 互斥事件:對任何二事件A 、B,若∅=B A ,則稱A 、B 二事件為「互斥事件」14. 餘事件:事件A 之互補事件,稱為A 之「餘事件」,記為c A 或A15. 狄摩根定理:對於事件A 、B,下列等式成立c c c B A B A )( =c c c B A B A )( =16. 交換律:(1)A B B A =(2)A B B A =17. 結合律)()(C B A C B A =)()(C B A C B A =18. 分配律)()()(C B C A C B A =)()()(C B C A C B A =二、排列與組合19. 階乘:當n 為大於或等於1之整數,則n 階乘定義為123)...2)(1(!⋅⋅--=n n n n ;而定義0!=120. 排列數:)!(!)1(2)-1)(n -n(n P n r r n n r n -=+-⋯=,其中n r ≤且r,n 均為大於或等於1的整數 21. 組合數:)!(!!!)1(2)-1)(n -n(n !C n rr n r n r r n r P n r -=+-⋯==,其中n r ≤且r,n 均為大於或等於1的整數三、機率概念與性質22. 事件之機率古典機率方法:在一隨機實驗,中若每一個結果產生的可能性一致的條件下,事件的機率為事件的元素個數除以樣本空間之樣本點的個數,即事件E 的機率:(S)#(E)#P(E)=,其中#(E)、#(S)分別代表事件E 及樣本空間S 的元素個數。