当前位置：文档之家 › 数据包络分析DEA教程(全)PPT

数据包络分析DEA教程(全)PPT

  • 格式：ppt
  • 大小：778.50 KB
  • 文档页数：43

下载文档原格式

  / 43

合集下载

DEA数据包络分析ppt课件

DEA数据包络分析ppt课件
DEA資料包絡分析法與選股 應用之探討
1
資料包絡分析法之基本模式與應用
基本概念 CCR模式
•投入導向 •產出導向 比率式、原問題、對偶問題 BCC模式 •投入導向 •產出導向 DEA執行程序 生產效率(整體技術效率)、(純)技術效率與 規模效率 交叉效率、FPI與A&P效率概念 案例討論與研析
c
SI2
S’
S
I2 I’b2
X2 I’2 a
µ¥ »ù ®æ ½u
A =P1X1+P2X2
A”
A’ S’µ¥ ²£ ¶q ½u
O
X1
I’1 I1
X1
5
基本觀念—生產前緣與包絡分析(續)
X2(I)
E B
D
C
A
X1(I)
6
CCR(Charnes, Cooper&Rhodes)模式—概念
理想假設 生產過程屬固定規模報酬，既是當投入量以等 比例增加時，產出亦應等比增加。
n
率)， ek Ekj /(n 1) 如此便可得出一個平均 j 1, j k
效率值，再依此平均效率值比較其效率之大小，此乃
所謂的交叉效率之分析。
28
交叉效率&FPI(False positive index)
但為證明此交叉效率之誤差性極大，筆者便以 Lindo所解出之權重與DEA Excel所得出的權重(兩 者權重不同)，以上述定義計算其效率，相互比較， 發現其差異甚大，故其結果並不可靠，必須加以 參考另一數值FPI(假正效率)， 即 M k (k ek ) ek ，依此評估其效率並相互比較，
其 值e越k 大越好， 越M小k 越好。
29

数据包络分析(DEA)详细教程44页PPT

数据包络分析(DEA)详细教程44页PPT
Thank you
39、没有不老的誓言，没有不变的承 诺，踏 上旅途 ，义无 ห้องสมุดไป่ตู้顾。 40、对时间的价值没有没有深切认识 的人， 决不会 坚韧勤 勉。
6、最大的骄傲于最大的自卑都表示心灵的最软弱无力。——斯宾诺莎 7、自知之明是最难得的知识。——西班牙 8、勇气通往天堂，怯懦通往地狱。——塞内加 9、有时候读书是一种巧妙地避开思考的方法。——赫尔普斯 10、阅读一切好书如同和过去最杰出的人谈话。——笛卡儿
数据包络分析(DEA)详细教程
36、“不可能”这个字(法语是一个字 )，只 在愚人 的字典 中找得 到。--拿 破仑。 37、不要生气要争气，不要看破要突 破，不 要嫉妒 要欣赏 ，不要 托延要 积极， 不要心 动要行 动。 38、勤奋，机会，乐观是成功的三要 素。(注 意：传 统观念 认为勤 奋和机 会是成 功的要 素，但 是经过 统计学 和成功 人士的 分析得 出，乐 观是成 功的第 三要素 。

《数据包络分析》课件

《数据包络分析》课件
《数据包络分析》PPT课件
目录
• 引言 • 数据包络分析的基本概念 • 数据包络分析的方法 • 数据包络分析的优化策略 • 数据包络分析的案例研究 • 数据包络分析的未来展望
01
引言
数据包络分析的定义
总结词
简明扼要地定义数据包络分析
详细描述
数据包络分析（Data Envelopment Analysis，简称DEA）是一种非参数的效率评估方法，用于评估决策单元（ DMU）的相对效率。它通过比较输入和输出的比率来评估效率，无需预先设定函数形式。
数据包络分析的应用领域
总结词
列举数据包络分析的应用领域
详细描述
数据包络分析广泛应用于各个领域，如金融、医疗、教育、供应链管理等。例如，在银 行业评估银行的相对效率，在医疗行业评估医院的医疗服务效率，以及在供应链管理中
评估供应商的相对效率。此外，DEA还可用于政策评估、环境影响评估等领域。
02
数据包络分析的基本概念
公共部门效率评估
总结词
通过数据包络分析评估公共部门的效率，提高公共服 务的水平和质量。
详细描述
数据包络分析可以用于评估公共部门的效率，通过构建 公共部门效率评估模型，利用公共部门的历史数据和公 共服务信息，计算出公共部门的效率值。根据效率值的 大小和变化趋势，可以分析公共部门在提供公共服务方 面的效率和存在的问题。同时，通过比较不同地区或不 同部门的效率值，可以发现公共服务的优势和不足，为 政策制定者和公共部门提供改进公共服务的建议和依据 。
04
数据包络分析的优化策略
决策单元的优化
01
决策单元选择
选择具有代表性的决策单元，确 保其涵盖了所有重要的变量和特 征。
02

DEA数据包络分析简明易懂ppt

DEA数据包络分析简明易懂ppt

通过输入输出指标的选择和模型计算，了解企业在各个层级的相对效
率，为企业决策提供有力支持。
DEA在政府决策中的应用案例
政策评估
DEA可以用于政策执行后的效果评估，通过输入输出 指标的选择和模型计算，评价政策的相对效率和效果 ，为未来政策制定和调整提供参考。
资源配置
政府可以利用DEA进行资源配置的优化，通过评估不 同部门或地区的相对效率和资源使用情况，进行资源 的合理调配和布局，实现资源的最大化利用。
06
总结与展望
DEA研究的主要结论
DEA模型的准确性和 效率
DEA模型在准确性和效率方面具有一 定的优势，能够有效地对多投入、多 产出的决策单元进行相对效率评价。
DEA模型的经济学含 义
DEA模型具有深刻的经济学含义，基 于生产前沿面的概念，可以很好地解 决多个输入和多个输出之间的权重问 题，避免了人为的主观判断。
01 02
小型企业
对于小型企业而言，DEA可以用于企业的相对效率评估，通过对比自 身和其他企业的效率，寻找提高效率的途径，促进企业的成长和发展 。
中型企业
中型企业可以利用DEA进行生产线的效率评估和优化，通过调整生产 线上的要素投入，追求更高的产出效率。
03
大型企业
对于大型企业而言，DEA可以用于企业的战略决策和资源配置优化。
DEA数据包络分析简明易 懂
xx年xx月xx日
contents
目录
• 引言 • DEA基本概念 • DEA模型的分析步骤 • DEA模型的拓展 • DEA的实践应用 • 总结与展望
01
引言
什么是DEA
• DEA（Data Envelopment Analysis，数据包络分析）是一种以相对效率评价为基础，用于评价一组多输 入、多输出决策单元（DMU）的相对效率或绩效的非参数方法。它广泛应用于不同行业和领域的效率评估 、决策制定等领域。

DEA方法简介.ppt

DEA方法简介.ppt

DEA方法以相对效率概念为基础，以凸分析和线形规 划为工具的一种评价方法，应用数学规划模型计算比较决 策单元之间的相对效率，对评价对象做出评价，它能充分 考虑对于决策单元本身最优的投入产出方案，因而能够更 理想地反映评价对象自身的信息和特点；同时对于评价复 杂系统的多投入多产出分析具有独到之处。
DEA方法的特点： ➢ 适用于多输出-多输入的有效性综合评价问题，在处理多
（D） n j y j s y 0 j 1 j 0,j 1,2, n 无约束，s 0,s 0
将上述规划（D）直接定义为规划（P）的对偶规划
几个定理和定义：
• 定理 1 线性规划（P）和对偶规划（D）均存在可行解， 所以都存在最优值。假设它们的最优值为别为hj0*与θ*， 则有hj0*＝ θ*
• 规划P的对偶规划为规划：
min
n
s.t. j x j x0 j 1 n
j y j y0 j 1
j 0, j 1,2, n 无 约 束
• 为了讨论和计算应用方便，进一步引入松弛变量s＋和 剩余变量s－，将上面的不等式约束变为等式约束，可 变成：
min
n
s .t . j x j s x 0 j 1
➢ DEA方法假定每个输入都关联到一个或者多个输出，且输 入输出之间确实存在某种联系，但不必确定这种关系的显 示表达式
二、 DEA基本原理和模型
定义：
权系数
1 2 3 … j …n
v1
1 x11 x12 x13 … x1j … x1n
v2
2 x21 x22 x23 … x2j … x2n
. . . . . . ….
（3）如果不存在λj*（j＝1，2，…，n）使得∑λj*＝1，若 ∑λj*＞1，则DMU为规模收益递减

数据包络分析DEAppt课件

数据包络分析DEAppt课件

经营者提供商品或者服务有欺诈行为 的，应 当按照 消费者 的要求 增加赔 偿其受 到的损 失，增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
2.1基本C2R模型
基本原理：设有n个决策单元，每个决策单 元均有m个输入指标和k个输出指标，记第j 个决策单元的第i个输入指标为xij,第j个决策 单元的第k个输出指标为ykj，vi为第i个输入 指标的权重，ui为第i个输出指标的权重，且 xij>0, ykj>0, vi ,ui≥0, 初始数据见表
对建筑业的线性规划模型为 max V 3573 1 6970 2 s.t.8124 1 12560 2 8420 3 3573 1 6970 2 0 60611 5230 2 4320 3 3510 1 5870 2 0 10130 1 4260 2 5820 3 4210 1 9120 2 0 20342 1 2310 2 12560 3 12680 1 21680 2 0 20561 1 1210 2 13510 3 21760 1 43250 2 0 4632 1 1790 2 12640 3 7920 1 21320 2 0 8124 1 12560 2 8420 3 1 1,2 ,3, 1, 2 0
生产函数上的B*点为技术有效性，弱有效 性。A点为规模有效性和技术有效性，有效 性。
生产可能集满足凸性、锥性、无效性、最小 性
经营者提供商品或者服务有欺诈行为 的，应 当按照 消费者 的要求 增加赔 偿其受 到的损 失，增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
DEA有效: 最优目标值h0= 1． DEA有效: 若存在最优解ω0,μ0满足ω0 >0,μ0 >0，h0 = μ0y0 = 1．

DEA数据包络分析法讲义.ppt

DEA数据包络分析法讲义.ppt

• 如以第j0个决策单元的效率指数为目标，以所有决策单元 的效率指数为约束，就构造了如下的CCR（C2R）模型：
s
ur yrj o
max hjo
r 1 m
vi xij o
i 1
s
ur yrj
s.t.
r 1 m
1, j 1,2, n
vi xij
i 1
u 0, v 0
• 上述规划模型是一个分式规划，使用Charnes－Cooper变 化，令：
.
ur
. . . . . …. .
ys1 ys2 ys3 … ysj … ysn s
us
权系数 s种输出
各字母定义如下：
• xij-------- 第j个决策单元对第i种类型输入的投入总量.xij〉0 • yrj-------- 第j个决策单元对第பைடு நூலகம்种类型输出的产出总量.yrj〉0 • vi -------- 对第i种类型输入的一种度量，权系数 • ur -------- 对第r种类型输出的一种度量，权系数 • i ----------1,2,…,m • r ----------1,2,…,s • j ----------1,2,…,n
• 对于每一个决策单元DMUj都有相应的效率评价指数：
s
hj
uT yi vT x j
ur yrj
r 1 mn
vi xij
,
j 1,2,
,n
i 1
我们总可以适当的取权系数v和u，使得 hj≤1, j=1,…，n
• 对第j0个决策单元进行效率评价，一般说来，hj0越大表 明DUMj0能够用相对较少的输入而取得相对较多的输出。 这样我们如果对DUMj0进行评价，看DUMj0在这n个 DMU中相对来说是不是最优的，我们可以考察当尽可能 的变化权重时， hj0的最大值究竟是多少。

第7章：数据包络分析ppt课件

第7章：数据包络分析ppt课件

………………………………………………
，…………………………
( x 1 n 1 x p n p ) ( y 1 n 1 y q n q ) 0 ，对应的对偶变量记为 n
x1k0 1 xp0k p1
i, j 0 ,i 1 ,2 , ,p ;j 1 ,2 , ,q
，对应的对偶变量记为
最新课件
3
二、C2R模型及其基本性质
1.C2R模型
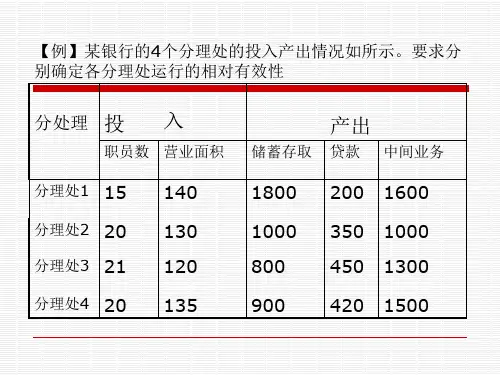
设有n个部门(企业)，称为n个决策单元，每个决策单元都有p种投入和q种产出，分 别用不同的经济指标表示。这样，由n个决策单元构成的多指标投入和多指标产出的评 价系统，可以用下图表示：
V 决策单元 1 2 … k … n
v1
→
x11 x12 … x1k … x1n
(P): MV ap xTY 0
(D ): MV iDn
k
s.t. T TX X0k
TYk
1
0,
(k1,2,,n)
,0
s.t. XkkSX0 k1
n
Yk k S Y0
k1
k 0 ,k 1 ,2 , ,n ;S ,S 0
定义7.1 如果线性规划(P)的最优解满足下列条件
VP = 0T · Y0 = 1
效率指标h0=hk0。在效率评价指标hk≤1(k=1,2,…，n)的约束条件下，选择一组最优权系数 U和V，使得h0达到最大值，构造优化模型(分式规划) ：
最新课件
5
q
uj yjk0
Ma h0x j p1
vi xik0
u1y1k0 v1x1k0
u2y2k0 v2x2k0
uqyq0k vpxp0k
最新课件
8
引入松弛变量 S(s1,s2, ,s p)T、 S(s1 ,s2 , ,sq )T, 将不等式约束化为等式约束，得

数据包络分析DEA教程(全)

数据包络分析DEA教程(全)

DEA的起源与发展
金融投资
在金融投资领域，DEA用于评估投资组合的相对效率，为投资者提供决策依据。
环境保护
在环境保护领域，DEA用于评估企业的环保投入与产出的相对效率，促进企业绿色发展。
公共部门
DEA也被广泛应用于公共部门，如政府机构、学校、医院等，用于评估其资源利用效率和改进方向。
运营管理
DEA被广泛应用于运营管理领域，用于评估企业的生产效率、资源配置效率和流程改进等方面。
02
随着DEA的应用范围不断扩大，许多学者对DEA模型进行了改进和发展。例如，Banker、Charnes和Cooper提出的BCC模型，解决了CCR模型中固定规模报酬假设的问题。
03
此外，DEA还与其他方法结合，如Malmquist指数、超效率DEA、方向距离函数等，进一步扩展了DEA的应用领域和评估准确性。
除了比率法和角度法，DEA有效性判定还可以采用其他方法，如SBM模型、全局DEA模型等。
03
CHAPTER
DEA的优化与改进
考虑了不同决策单元(DMU)在不同规模下的效率变化，能够更准确地评估DMU的效率。
总结词
规模报酬可变的DEA模型假设生产过程中可能存在规模效应，即随着生产规模的扩大，生产效率可能会提高。该模型通过调整权重来考虑不同规模下的效率变化，从而更准确地评估DMU的效率。
DEA的应用领域
02
CHAPTER
DEA基本模型
CCR模型
CCR模型（Charnes, Cooper和Rhodes模型）是最早提出的数据包络分析模型，用于评估决策单元（DMU）的相对效率。
02
CCR模型假设所有DMU都具有相同的输入和输出指标，并且规模报酬不变。

数据包络分析DEA课件

数据包络分析DEA课件
© 24
数据包络分析
© 25
数据包络分析
© 26
数据包络分析
© 27
数据包络分析
© 28
数据包络分析
© 29
数据包络分析
© 30
数据包络分析
© 31
数据包络分析
例 有4个银行储蓄所，每月完成10000笔人民币的 存款、取款业务，但其投入情况不同，见下表，试 分析这4个储蓄所的绩效。
储蓄所 职员数
DEA方法简介
数据包络分析方法（ DEA，Data Envelopment Analysis ）由 著名的运筹学家A.Charnes(查恩斯), W.W.Cooper(库伯), 及 E.Rhodes (罗兹) 于1978年提出，用于评价相同部门间的相对有 效性（也被称为DEA有效）。
该方法的原理主要是通过保持决策单元（DMU, Decision Making Units）的输入或者输出不变，借助于数学规划和统计数据确定相 对有效的生产前沿面，将各个决策单元投影到DEA的生产前沿面 上，并通过比较决策单元偏离DEA前沿面的程度来评价它们的相 对有效性。
©6
数据包络分析
• 数据包络分析是一种对具有相同类型决策单元进行绩效 评价的方法。
• DMU：效率的测度对象，任何具有可测量的投入、产出 的部门、单位或个人，但必须具有可比性
• 这里相同类型是指这类决策单元具有相同性质的投入和 产出，如医院投入的是医护人员、面积、床位数、医疗 设备和药品等，产出是门诊病人人次、住院病人人日、 代培实习的医护人员数等。
（2）建模计算阶段 建立评价指标体系 选择决策单元
© 14
数据包络分析
收集和整理的数据具有可获得性 选择适当的DEA模型进行计算 （3）分析结果阶段 对结果进行比较和分析，找出无效单元无效的原因，并提供进一步 改进的途径 根据定性的分析和预测的结果来考察评价结果的合理性

DEA数据包络分析ppt课件

DEA数据包络分析ppt课件
24
y
DMU3
DMU2
DMU4
DMU1
o
x
DMU1、 DMU2、 DMU3都处于技术有效状态；DMU1不为规模有效， 实际上它处于规模收益递增状态； DMU3不为规模有效，实际上它处于 规模收益递减状态； DMU2是规模有效的。如果用DEA模型来判断DEA 有效性，只有DMU2对应的最优值θ0＝1。可见，在C2R模型下的DEA有 效，其经济含义 是：既为“技术有效”，也为“规模有效”。
项产出均不低于 j0 决策单元的各项产出，它的各项投入均 低于 j0 决策单元的各项的各项投入。
即有：
n
∑j=1j yrj ≥ yrj0
（r = 1，2，…，s）
n
∑j=1j xij ≤ E xij0
n
∑j=1j = 1
，j ≥0
（i = 1，2，…，m，E＜1）
（j = 1，2，…，n）
这说明 j0 决策单元不处于生产前沿面上。
16001 +10002 +13003 +15004 ≥1600
S.t.
151 + 202 + 213 + 204 ≤ 15E
1401 + 1302 + 1203 + 1354 ≤140E
1 +
2 +
3 +
4 = 1
j ≥0 （ j = 1，2，3，4 ）
29
例4：银行分理处相对有效性评价
求解结果分析： 对分理处1，E =1，说明分理处1的运行DEA有效。 对分理处2，E =0.996，说明分理处2的运行非DEA有
分理处3 21
120
800 450 1300

DEA数据包络分析(简明易懂版)ppt

DEA数据包络分析(简明易懂版)ppt
生热量的理想值）
• yr同样量的煤用这个装置所产生的热量（实测 值）
• 0《Er《1
2020/5/15
-
11
相对有效性评价问题举例
例2：银行分理处相对有效性评价
振华银行的 4 个分理处的投入产出如下表。求各个分理处的运
行是否DEA有效。
（产出单位：处理笔数/月）
分理处
投入
产出
职员数 营业面积（m2） 储蓄存取 贷款 中间业务
分理处1 15 分理处2 20 分理处3 分理处4 20
140
1800 200 1600
130
1000 350 1000
120
800 450 1300
135
900 420 1500
-
例2：银行分理处相对有效性评价
求解结果分析： 对分理处1，E =1，说明分理处1的运行DEA有效。 对分理处2，E =0.996，说明分理处2的运行非DEA有
• 因而，需采用一种全新的方法进行绩效比较。这种方法就 是二十世纪七十年代末产生的数据包络分析（DEA）。 DEA方法处理多输入，特别是多输出的问题的能力是具有 绝对优势的。
2020/5/15
-
3
数据包络分析（DEA）源起
1978年，著名运筹学家、美国德克萨斯大学教授 A.Charnes及W.W.Cooper和E.Rhodes发表了一篇重要论 文：“Measuring the efficiency of decision making units”（决策单元的有效性度量），刊登在权威的“欧洲运 筹学杂志”上。正式提出了运筹学的一个新领域：数据包 络分析，其模型简称 C2R 模型。该模型用以评价部门间的 相对有效性（因此被称为DEA有效）。

数据包络分析DEA ppt课件

数据包络分析DEA ppt课件
数据包络分析DEA
数据包络分析DEA
重要的是“会什 么”，而不是“为什
么”
数据包络分析DEA
▪ 复旦大学现代哲学研究所所 长：俞吾金
舍恩伯格说：“是什么”往往比“为什么”重要。 俞吾金：为什么还有《十万个为什么》？ 大家怎么看？ 刘永亮的观点：哲学，我不说。对于应用统计学者， 是什么，为什么，都不重要。会什么才重要。
▪ 产出松驰度：三个产出指标，11个公司 ▪ 企业3：指标2增加13.234个单位，指标3增加12.764
个单位，就有效了
▪ 其它企业：依此类推。
▪ 投入松驰度（或称冗余）：第1,2个企业是有效的， 所以，投入没有冗余。
▪ 企业3：前三种投入没有冗余，第4种投入，冗余 了27.572。实践意义？
标3增加724个单位，就最优了。
数据包络分析DEA
▪ 哪些企业最优？1, 2,4和 .企业3如何调整？ ▪ 产出不变条件下，第二项投入减少166.9个单位，
同时第3项投入减少342个单位，就最优了。
数据包络分析DEA
▪ 第3个企业第2个产出指标目标是多少？ ▪ 54.814。现实情况是多少？35。
▪ 规模无效，技术也无效 （都小于1）
▪ irs何意？ ▪ Increasing，递增，decreasing，递减，
constant，不变 ▪ irs是规模报酬递增，实践意义？
数据包络分析DEA
▪ 规模报酬：不变、递增、递减三种情况
▪ 不变规模报酬：crs，constant return to scale ▪ 递增规模报酬：irs，increasing return to scale
数据包络分析DEA
▪ 哪儿的点有效，哪儿的点无效？ ▪ 线上的点有效，线右边的点无效。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

j 1
（D）
n
j y j s y0 j 1
j 0, j 1,2, n
无约束，s 0, s 0
将上述规划（D）直接定义为规划（P）的对偶规划
几个定理和定义：
• 定理 1 线性规划（P）和对偶规划（D）均存在可行解， 所以都存在最优值。假设它们的最优值为别为hj0*与θ *， 则有hj0*＝ θ *
定义1 若线性规划（P）的最优值hj0*＝1，则称决策单元 DMUj0为弱DEA有效
定义2 若线性规划（P）的解中存在w*＞0，μ * ＞0， 并且最优值hj0*＝1，则称决策单元DMUj0为DEA有效的
• 定理2 DMUj0 为弱DEA有效的充要条件是线性规划 （D）的最优值θ *＝1； DMUj0为DEA有效的充要条件是 线性规划（D）的最优值θ *＝1，并且对于每个最优解λ *， 都有s*＋＝0，s*-＝0
• 上述规划模型是一个分式规划，使用Charnes－Cooper变 化，令：
t

1 vT x0
,
w

tv,


tu
由t

1 vt x0

wt x0
1
可变成如下的线性规划模型P：
max hj0 T yo
（P）
s.t.wT x j T y j 0, j 1,2,n
wT x0 1
.
ur
. . . . . …. .
ys1 ys2 ys3 … ysj … ysn s
us
权系数 s种输出
各字母定义如下：
• xij-------- 第j个决策单元对第i种类型输入的投入总量.xij〉0 • yrj-------- 第j个决策单元对第r种类型输出的产出总量.yrj〉0 • vi -------- 对第i种类型输入的一种度量，权系数 • ur -------- 对第r种类型输出的一种度量，权系数 • i ----------1,2,…,m • r ----------1,2,…,s • j ----------1,2,…,n
• 如以第j0个决策单元的效率指数为目标，以所有决策单元 的效率指数为约束，就构造了如下的CCR（C2R）模型：
s
ur yrj o
max hjo

r 1 m
vi xij o
i 1
s
ur yrj
s.t.
r 1 m
1, j 1,2,n
vi xij
i 1
u 0, v 0
vi
.. .
.
. Xij … .
. . . . . . ….
vm
m xm1 xm2 xm3 … xmj … xmn
n个 决策单元 （DMU）
m种输入
y11 y12 y13 … y1j … y1n
1
u1
y21 y22 y23 … y2j … y2n 2
u2
. . . . . …. .
...
. yrj … .
输出-多输入的有效性评价方面具有绝对优势 DEA方法并不直接对数据进行综合，因此决策单元的最优
效率指标与投入指标值及产出指标值的量纲选取无关，应 用DEA方法建立模型前无须对数据进行无量纲化处理（当 然也可以）
DEA方法的特点：
无须任何权重假设，而以决策单元输入输出的实际数据求 得最优权重，排除了很多主观因素，具有很强的客观性
（D/）
min
n
s.t. j x j x0 j 1
n
j y j y0 j 1
j 0, j 1,2, n
无 约 束
• 为了讨论和计算应用方便，进一步引入松弛变量s＋和
剩余变量s－，将上面的不等式约束变为等式约束，可
变成：
min
n
s.t.
j x j s x0
DEA方法假定每个输入都关联到一个或者多个输出，且输 入输出之间确实存在某种联系，但不必确定这种关系的显 示表达式
二、 DEA基本原理和模型
定义：
权系数
1 2 3 … j …n
v1
1 x11 x12 x13 … x1j … x1n
v2
2 x21 x22 x23 … x2j … x2n
. . . . . . ….
w 0, 0
• 利用线性规划的最优解来定义决策单元j0的有效性，从 模型可以看出，该决策单元j0的有效性是相对其他所有决 策单元而言的。
• 对于CCR模型可以用规划P表达，而线性规划一个重要 的有效理论是对偶理论，通过建立对偶模型更容易从理论 和经济意义上作深入分析
• 规划P的对偶规划为规划D/：
应用DEA方法对经济体 效率的评价
西安交大经济管理学院
目 录：
一、 DEA方法简介 二、 DEA基本原理和模型 三、 DEA应用案例 四、 DEA软件介绍 五、 DEA主要应用领域 六、 DEA最新研究进展 七、DEA主要参考文献
一、 DEA方法简介
数据包络分析方法（ DEA，Data Envelopment Analysis ）由Charnes、Coopor和Rhodes于1978年提出， 该方法的原理主要是通过保持决策单元（DMU, Decision Making Units） 的输入或者输入不变，借助于数 学规划和统计数据确定相对有效的生产前沿面，将各个决 策单元投影到DEA的生产前沿面上，并通过比较决策单元 偏离DEA前沿面的程度来评价它们的相对有效性。
• 对于每一个决策单元DMUj都有相应的效率评价指数：
s
hj

uT yi vT x j
ቤተ መጻሕፍቲ ባይዱ

ur yrj
r 1 mn
vi xij
,
j 1,2,, n
i 1
我们总可以适当的取权系数v和u，使得 hj≤1, j=1,…，n
• 对第j0个决策单元进行效率评价，一般说来，hj0越大表 明DUMj0能够用相对较少的输入而取得相对较多的输出。 这样我们如果对DUMj0进行评价，看DUMj0在这n个 DMU中相对来说是不是最优的，我们可以考察当尽可能 的变化权重时， hj0的最大值究竟是多少。
DEA方法以相对效率概念为基础，以凸分析和线形规 划为工具的一种评价方法，应用数学规划模型计算比较决 策单元之间的相对效率，对评价对象做出评价，它能充分 考虑对于决策单元本身最优的投入产出方案，因而能够更 理想地反映评价对象自身的信息和特点；同时对于评价复 杂系统的多投入多产出分析具有独到之处。
DEA方法的特点： 适用于多输出-多输入的有效性综合评价问题，在处理多