数据包络分析ppt课件

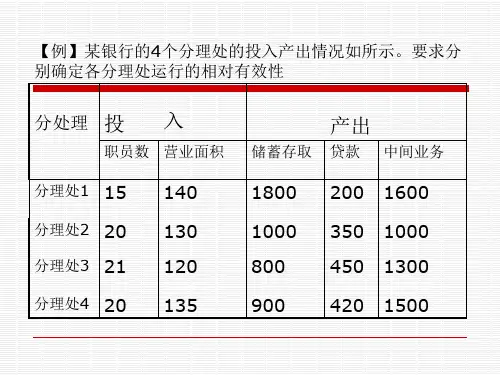
数据包络分析法（见课件）数据包络分析（Data Envelopment Analysis ， 简称DEA ）是著名运筹学家A.Charnes 和W.W.Cooper 等学者在“相对效率评价”概念基础上发展起来的一种新的系统分析方法．DEA 方法的一些基本概念比较抽象，应用又涉及较多的知识领域．考虑到本书读者的具体情况和篇幅所限，本节只介绍其在卫生管理中的部分应用，希望对卫生管理人员了解DEA 方法、提高管理工作和系统分析能力起到积极作用．一、基本概念1．决策单元卫生管理工作可以看作是一个地区、一个医院、一所医学院校等的决策层（单元）在一定可能范围内，通过一定数量的…投入‟产生出一定数量的…产品‟的活动．虽然这种活动的具体内容不同，但其目的都是尽可能使这一活动取得最大的…效益‟．由于从…投入‟到…产出‟需要经过一系列的决策才能实现，即…产出‟是…决策‟的结果，这样的单元称为决策单元．2．输入与输出在卫生管理工作中经常需要对具有相同类型的部门或单位（决策单元）进行评价，其评价的依据是决策单元的…输入‟和…输出‟数据． 输入数据是指决策单元在某种活动中需要耗费的某些资源数量，例如投入的资金、劳动力、占地面积等等；输出数据是指决策单元经过一定的输入之后，产生的表明该活动成效的某些信息．比如评价一所高等院校，输入可以是全年的资金、教职员工总数、用房总面积、各类职称专业人员数等等，输出可以是培养的博士研究生人数、硕士研究生人数、本科生人数、各类科研成果数量、学生质量等等．根据输入数据和输出数据评价决策单元的优劣．决策单元在将输入转化成输出的过程中实现自身的决策目标．3．有效生产活动设某个决策单元DMU 在一项…经济‟（生产）活动中的输入向量为Tm x x x x ),,,(21 =，输出向量为Ts y y y y ),,,(21 =，于是我们可以简单地用),(y x 表示这个DMU 的整个生产活动．称}),{(生产出来能用产出x y y x T =为所有可能的生产活动构成的生产可能集．设T y x ∈),(，如果不存在T y x ∈),('，且'y y ≤，则称),(y x 为有效生产活动． 4．规模有效如果投入增量相对百分比)(xx ∆大于产出增量相对百分比)(yy∆，表明投入规模的增加并未获得…理想‟的产出效果，故称为规模效益递减，反之如果投入增量相对百分比)(xx ∆小于产出增量相对百分比)(y y∆，表明产出效益相对增加大于投入规模的相对增加，则称为规模效益递增，如果)(xx ∆等于)(yy∆则为规模效益不变．如果某一生产过程),(0y x 处于规模效益递增状态，说明在0x 的基础上，适当增加投入量，可望最大产出有相对更大比例的增加，因此决策单元（DMU ）会有增加投入的积极性，反之将没有再增加投入的积极性．如果对于投入规模0x ，当投入小于0x 时，均为效益递增状态，而当投入大于0x 时，均为效益递减状态，即就投入规模而言，无论大于或小于0x 都不是最好的，我们称这样的DMU 对应的生产过程)(0,0y x 为规模有效的．二、DEA 方法的基本思路设有八所类型相同的医院，每所医院有两种投入，一种产出，各自的投入与产出情况见表12—6 ，如何对这八所医院的优劣进行评价？表12—6 各医院投入与产出情况为便于比较，对各医院的投入与产出以相同比例扩大，并使每所医院的产出均变为120，这样得到表12—7我们以投入1、投入2与产出为坐标，在投入——产出空间中标出这八个点，再将它们投影到投入平面上（如图12—2所示）．现在把jDMU（j =773引伸出的水平、垂直线，就得到由部分DMU 构成的分线段的“最小凸包”，而所有的jDMU 都位于这个最小凸包的右上方．下面我们把所有八个点与原点O 连接起来，点O 与8DMU 、2DMU、4DMU的连线分别与凸包交于A 、B 、C 点，其中A 点在6DMU与 1DMU 的连线上，因为A 点的坐标与8DMU 的坐标对应成比例，故可设为为（2x ，x ），经过以下计算：610193010192--=--xx 79.9=x故A 点的坐标为（19.58，9.79），产出也为120，反过来既然ADMU 的产出也为120，那么根据8DMU的实际投入，它的产出应为1.14758.1924120=⨯但它现在实际产出只有120，这说明8DMU的生产过程不是有效的，同理2DMU4DMU也不是有效的，并且距最小凸包越远，其有效性越差．我们不妨用OAO 8来评价8DMU的有效性，这里226.158.19248==OAO ＞1这个量越大非有效性越显著．由于分段线性的“最小凸包”是在有限多个实际生产观测值基础上构成的最理想（最前沿）的边界，如果实际观测值足够多，那么折线将接近圆滑曲线，这样原来边界上的点可能不全在曲线上，即不再都是有效的．因此，上述方法判断某个DMU 是否是有效的是相对于一组实际观测值而言的，即我们所说的有效性是某种意义下的相对有效性．相对于某一个非边界DMU 构造出一个新的各投入分量相对较少的DMU ，这种构造实际上是通过对各已知DMU 的线性组合来实现的，这样我们就可以用线性规划为基本模型并结合其他分析手段和方法，来比较各DMU 之间的相对有效性．对多维输入、输出的情况下，要注意在综合过程中确定各输入、输出的权重．线性规划模型是如何被导入DEA 方法的？针对表12—6 投入与产出数据建立如下线性规划模型：（一） 输出型 例如，我们想判断8DMU是否为最优，即8DMU在实际投入量不减少的情况下，其最大产出量还能有所增加吗？为此我们建立如下的线性规划模型：ϖmax44810102131987654321≤+++++++λλλλλλλλ 22121715631087654321≤+++++++λλλλλλλλ ϖλλλλλλλλ2020244012040242412087654321≥+++++++0≥i λ 8,,2,1 =i如果最优解1*>ϖ，说明这个新的DMU 的产出＞20，这也从另一个侧面告诉我们，原来的8DMU不是最优的．事实上在这个例子中，最优解1935.0*1=λ，0323.0*6=λ，0*=j λ（j=2，3，4，5，7，8），259.1*=ϖ这一结果表明，由0.1935倍的1DMU 与0.0323倍的6DMU 的投入之和重新构成的新的*8DMU与原来的8DMU相同，但却能得到8DMU产出的1.2259倍，即20×1.2259=24.518，因此，相对来说，原来8DMU 不是有效的．这个结果与前面OAO 8的结果是一致的．（二） 输入型如果保持8DMU的产出量不减，能否使其原来的各投入按某个比例降低，或者说对于8DMU的原产出量其最小投入量究竟是多少？为此构造如下的线性规划模型：θminθλλλλλλλλ44810102131987654321≤+++++++ θλλλλλλλλ22121715631087654321≤+++++++ 2020244012040242412087654321≥+++++++λλλλλλλλ0≥i λ 8,,2,1 =i若θ＜1，说明新组合而成的DEA 投入量更小，则原8DMU不是有效的．解此线性规划问题，最优解1579.0*1=λ，0263.0*6=λ，0*=j λ（j=2，3，4，5，7，8），8158.0*=θ，故原8DMU不是有效的．(其中，松弛变量的值为1053.01=-s ，2895.02=-s ，0408.03=+s )．此结果表明，由0.1579倍的1DMU 与0.0263倍的6DMU 组合成一个新的*8DMU与原来的8DMU产出相同，但各投入量却减至原来的0.8158，即投入1为4×0.8158=3.2632，投入2为2×0.8158=1.6316．具体问题选用输入或输出哪个模型一要看DMU 的实际经济背景，二要看评价目的．如果输入指标不易有较大变动或基本保持在一定水平上，这时选用基于输出的DEA 模型较合适，反之若输出指标不易有较大变动，如输出标准已确定，由于对其有较严格的限制，这时选用基于输入的DEA 模型较合适．三、DEA 的基本模型——R C 2模型 （一）R C 2模型 设有n 个jDMU（n j ,,1 =）jDMU的输入、输出向量分别为Tmj j j j x x x x ),,,(21 =＞0 Tsj j j j y y y y ),,,(21 =＞0对固定的0j )1(0n j ≤≤，构造如下两个线性规划模型 LP1：寻求jDMU)1(n j ≤≤的一种线性组合，在不比0j DMU原来投入更多的前提下，求其最大可能产出量，并检查这一产出量是否比原产出更多．相应模型为：*=ϖϖmax∑=≤nj j i j i jx x 10λ，m i ,,1 =ϖλ∑=≥nj j k jkjy y 10，s k ,,1 = （12—2）0,0≥≥ϖλj n j ,,1 =式中m 为投入个数，s 为产出个数，n 为决策单元个数．()n j j,,2,1 =λ为n 个DMU 的某种组合权重，∑=nj j j x 1λ和∑=nj j jy 1λ为按这种权重组合的虚构DMU 的投入和产出向量，0j i x 和0j k y 为所评价的第0j 个DMU 的投入和产出向量．该模型是从投入不变，产出增加的角度构造的，用于研究产出的有效性．同理，从产出不变投入减少的角度可构造模型来研究投入的有效性．LP2：寻求jDMU)1(n j ≤≤的一种线性组合，在至少保持0j DMU产出量的前提下，求其最小投入量，并检查这一投入量是否比原投入更小．相应模型如下：*=θθminθλ∑=≤nj j i j i jx x 10，m i ,,1 =∑=≥nj j kjkjy y 1λ，s k ,,1 = （12—3）0,0≥≥θλj n j ,,1 =以上两个模型可写成：⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧≥≥=≥=-=+=-++=-=*∑∑0,0,,2,1,0max 101s s n j y s y x s x jjonj jj j nj j j λϖλλϖϖ （12—4） 和⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧≥≥=≥=-=+=-++=-=*∑∑0,0,,2,1,0min 101s s n j y s y x s x jjonj jj j nj j j λλθλθθ （12—5） 其中+s 和-s 为松弛变量．以上四个模型称为R C 2模型．以下主要讨论模型（12—5），研究投入的有效性． （二）DEA 有效性（R C 2）以下从应用的角度不加证明地直接给出由模型（12—5）判断DEA 有效性定理，它本质上就是在模型（12—5）下弱DEA 有效和DEA 有效的定义．定理12—1 对于线性规划（12—5）有1．若模型（12—5）最优植1=*θ ，则第0j 个DMU 为弱DEA 有效，反之亦然； 2．若模型（12—5）的最优植1=*θ ，并且满足所有的0=*-s 、0=*+s（每个分量都为零），则第0j 个DMU 为DEA 有效，反之亦然．实际中如何对多个DMU 进行相对有效性评价呢？由定理12—1可知，如果模型（12—5）的最优植1<*θ ，这说明第0j 个DMU 不是弱DEA 有效，当然更不是DEA 有效的．也就是说，它是非DEA 有效的，并且*θ越小，其有效性越差．但若用模型（12—5）判定某个DMU 为DEA 有效，就需要检查所有的解**-*+*θλ,,,s s 都满足,0,0,1===*-*+*ssθ如果只有1=*θ，但并非所有的0=*-s，0=*+s，只能说明第0j 个DMU 是弱DEA 有效，不能说是DEA 有效．但对于模型（12—5）要判断所有的0=*-s ，0=*+s，并不是一件容易事，因此，在实际中经常直接使用的并非模型（12—5），而是一个稍加变化了的模型，这个模型就是所谓具有非阿基米德无穷小ε的R C 2模型．非阿基米德无穷小ε是一个抽象的数学概念，可以理解为一个小于任意正数而大于零的数（实际使用中常取为足够小的正数，例如610-）．带有非阿基米德无穷小ε的R C 2模型为：()[]⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧≥≥=≥=-=+=+--++=-=*+-∑∑0,0,,2,1,0ˆmin 101s s n j y s y x s x s e s e jjonj jj j nj j j T T λλθλθεθ （12—6） 其中m T R e∈=)1,,1(ˆ ，s T R e ∈=)1,,1( 定理12—2 设ε为非阿基米德无穷小，以上该线性规划问题的最优解为**-*+*θλ,,,ss1． 若1*=θ，则0j DMU 为弱DEA 有效；2． 若1*=θ，且0=*+s，0=*-s ，则称0j DMU为DEA 有效．（三）DEA 有效性（R C 2）的经济含义如果把相同类型的DMU 看成是某种“生产”活动，则DEA 有效性具有一定的经济含义：在R C 2模型下为DEA 有效的DMU ，从生产函数的角度讲，既是“技术有效”的，也是“规模有效”的．由DEA 有效性定理可分为以下三层含义：1．如果1<θ，在保持产出0j y 不变的前提下，可以将投入0j x 的各个分量均按同一比例减少，则表明可以用比0j DMU更少的投入而使产出不变，这正说明当前的0j DMU不是有效的生产活动，其既非技术有效也非规模有效．2．如果1=θ，要保持产出0j y 不变，投入0j x 的各个分量不可以全部继续减少，但可以作到减少部分投入，而保持产出0j y 不变，则表明当前的0j DMU 是弱DEA 有效，但不是DEA 有效．从生产理论来讲，它是技术有效而非规模有效．3．如果1=θ，要保持产出0j y 不变，投入0j x 的各个分量不仅不能整体按比例减少，而且连部分投入也不能再减少，则表明当前的0j DMU 是DEA 有效的，从生产理论来讲，它既是技术有效的也是规模有效的． 四、非有效DMU 的改善本章开始给出的对八所医院的评价问题中决策单元1DMU ，3DMU，5DMU，6DMU，7DMU，是相对有效的，而2DMU，4DMU，8DMU不是有效的，那么我们怎样将非有效的DMU 变成有效的DMU 呢？在保持目前输出水平的前提下，要使非有效的DMU 变成相对有效的，它的各输入指标应有所减少，减少到多少呢？如果用0x ，0y 表示原某非有效的DMU 的输入与输出向量， 线性规划问题θmin01x s x nj j jθλ∑=-=+，∑=+=-nj j jy sy 10λ，,0≥j λ n j ,,1 =0,0≥≥+-ss的最优解为θλ,,,+-s s ，那么--=s x x00ˆθ ++=s y y00ˆ 相对于原来的DMU 来说是有效的． 以输入型，8DMU为例原来是非有效的．我们已经得到 8158.0*=θ，1053.01=-s ，2895.02=-s ，0408.03=+s原8DMU投入1为4，投入2为2，要使它变成相对有效的，它的各输入指标应减少到： 1579.31053.048158.0ˆ111=-⨯=-=-s x xθ 3421.12895.028158.0ˆ222=-⨯=-=-s x x θ则相对于原来的DMU 来说就是有效的了．如果新的“理论值”难以实施，可对原来的输入、输出指标体系进行某些修正，并根据新的指标体系再进行DEA 分析，并从DEA 相对有效性值的变化中提取有用的管理信息．五、应用DEA 方法需要强调的几个问题在进入实际应用前还需要强调以下几个问题：1．R C 2模型是DEA 方法中最基本的模型，由于实际生产过程和经济活动的多样性，在这个模型基础上又派生出了一些新的模型，比如：22S G C 可以评价技术有效性；W C 2模型可以处理无穷多个决策单元；锥比率H W C 2模型可以处理具有过多投入和产出的情况，并且锥的选取可以体现决策者或评价者的偏好；还有D C -型DEA 模型，含有偏好信息的DEA模型等．在实际应用前可以根据评价的目的选择适宜的方法．2．评价对象是同种类型的DMU，既可以横向对比，也可以纵向对比．3．由于DEA方法并不直接对指标数据进行综合，因而建立模型前无需对数据进行无量纲化处理．可以证明，某个DMU的相对有效性评价结果与各投入产出指标的量纲选择无关．4．通过对DEA模型求解可以将参评的多个DMU分成三类：第一类是DEA有效的DMU，第二类是仅为弱DEA有效的DMU，第三类是非DEA有效的DMU，这三类显然已经序化，依次由“好”到“不好”，对于第一类DMU，DEA方法并不做出排序，对于第二类θ）DMU，也不做出排序，对于第三类DMU可按各DMU的相对有效性值（即模型的最优值*θ越小其相对有效性越差．另外，更为重要的是，对第二类和第三类DMU可以来排序，*找出其“生产”过程中问题所在，为管理提供更为丰富的信息．六、DEA方法应用的一般步骤虽然DEA实际应用所涉及的领域不同、目的不同，但DEA方法在应用步骤上有若干共同点．DEA方法的一般步骤是：1．确定评价目的DEA方法的基本功能是“评价”，特别是进行多个同类样本间的“相对优劣性”的评价．为此需要明确哪些DMU能够或适宜在一起进行评价，通过什么样的输入/输出指标体系进行评价，选择什么样的DEA模型进行评价等，这些均应服从于应用DEA方法的具体目的性．2．选择DMU选择DMU就是确定参考集．由于DEA方法是在同类的DMU之间进行相对有效性的评价，因此选择DMU的一个基本要求就是DMU的同类型．同类型应具有三个基本特征：①具有相同的目标和任务；②具有相同的外部环境；③具有相同的输入和输出指标．如果将较多的DMU放在一起组成一个参考集时，“同类型”反映得不够充分，若将它们按一定特性分成几个子集，则每个子集内的DMU较好地体现出“同类型”．这样我们可以分别对这几个子集进行DMU分析，再将分析结果或独立或综合地进行再分析，这样往往能得到一些新的有用信息．3．建立输入/输出指标体系建立输入/输出指标体系是DEA方法的一项基础工作，有几点要注意：第一，要考虑能够实现评价目的，即输入与输出向量的选择要服务、服从评价目的；第二，要能全面反映评价目的；第三，要考虑输入向量、输出向量之间的联系．如果某指标与已作为输入（出）指标之间呈现较强相关关系，则不要再选入．如果某指标与诸输入相关关系较强而同时又与诸输出相关关系较弱，则可将该指标归为输出，反之则归为输入．权重很小的指标可以考虑删除；第四，要考虑输入/输出指标体系的多样性．一般在实现评价目的的大前提下，设计多个输入/输出指标体系，对各体系进行DEA分析后，将分析结果放在一起进行比较分析．4．DEA模型的选择DEA模型有多种形式，选择哪个一要看DMU的实际背景，二要看评价目的．此外评价中要对各指标的相对重要性有所体现．尽可能选用不同类型同时进行分析，再把分析结果相互比较，这样会使评价更全面、更准确．5．评价工作的表述经过建模、求解，一般需从各DMU的DEA有效性、DMU的相对规模收益、相对有效前沿面、非有效DMU的改善以及各DMU的相对有效性与输入/输出指标之间的关系等方面予以表述．。