当前位置：文档之家 › 信息论基础第5章无失真信源编码[56页]

信息论基础第5章无失真信源编码[56页]

  • 格式：ppt
  • 大小：4.60 MB
  • 文档页数：30

下载文档原格式

  / 30

合集下载

信息论：第5章 无失真信源编码定理

信息论：第5章 无失真信源编码定理
23
（7）码的N次扩展码
假定某码C，它把信源 S {s1 , s2 ,, sq }中的符号
s i 一一变换成码C中的码字 Wi ，则码C的N次扩展 码是所有N个码字组成的码字序列的集合。
24
例如：若码 C {W1 ,W2 ,,Wq } 满足：si Wi ( xi1 , xi 2 ,, xil ), si S , xil X 则码C的N次扩展码集合 B {B1 , B2 , , Bq } ,其中：
为了解决这两个问题，就要引入信源编码和信 道编码。
2
一般来说，抗干扰能力与信息传输率二者相互矛盾。 然而编码定理已从理论上证明，至少存在某种最佳 的编码能够解决上述矛盾，做到既可靠又有效地传 输信息。 信源虽然多种多样，但无论是哪种类型的信源， 信源符号之间总存在相关性和分布的不均匀性，使 得信源存在冗余度。
q r
N
l
（5.2）
36
25
（8）惟一可译码
若任意一串有限长的码符号序列只能被惟一地 译成所对应的信源符号序列，则此码称为惟一可译 码（或称单义可译码）。否则就称为非惟一可译码 或非单义可译码。
若要使某一码为惟一可译码，则对于任意给定 的有限长的码符号序列，只能被惟一地分割成一个 个的码字。
26
例如：对于二元码 C1 {1, 01, 00}，当任意给定一串 码字序列，例如“10001101”，只可唯一地划分为 1,00,01,1,01，因此是惟一可译码； 而对另一个二元码 C 2 {0,10, 01}，当码字序列 为“01001”时，可划分为0,10,01或01,0,01，所以是 非惟一可译的。
i
N
Bi {Wi1 ,Wi2 ,,WiN }; i1 ,, i N 1,, q; i 1,, q N

信息论常用无失真信源编码设计(含MATLAB程序)

信息论常用无失真信源编码设计(含MATLAB程序)

《信息论基础》题目：常用无失真信源编码程序设计目录1. 引言 (2)2. 香农编码 (2)2.1 编码步骤 (3)2.2 程序设计 (3)2.3 运行结果 (3)3. 费诺编码 (4)3.1 编码步骤 (5)3.2 程序设计 (5)3.3 运行结果 (5)4. 哈夫曼编码 (6)4.1 编码步骤 (7)4.2 程序设计 (7)4.3 运行结果 (8)5. 结论 (9)6. 参考文献 (10)7. 附录 (11)7.1 香农编码Matlab程序 (11)7.2 费诺编码Matlab程序 (12)7.3 哈夫曼编码Matlab程序 (14)1. 引言信息论（Information Theory）是运用概率论与数理统计的方法研究信息、信息熵、通信系统、数据传输、密码学、数据压缩等问题的应用数学学科。

信息系统就是广义的通信系统，泛指某种信息从一处传送到另一处所需的全部设备所构成的系统。

信息论是关于信息的理论，应有自己明确的研究对象和适用范围[1]。

信息论将信息的传递作为一种统计现象来考虑，给出了估算通信信道容量的方法。

信息传输和信息压缩是信息论研究中的两大领域。

这两个方面又由信息传输定理、信源－信道隔离定理相互联系。

信源编码是一种以提高通信有效性为目的而对信源符号进行的变换，或者说为了减少或消除信源冗余度而进行的信源符号变换。

具体说，就是针对信源输出符号序列的统计特性来寻找某种方法，把信源输出符号序列变换为最短的码字序列，使后者的各码元所载荷的平均信息量最大，同时又能保证无失真地恢复原来的符号序列[2]。

在通信中，传送信源信息只需要具有信源极限熵大小的信息率，但在实际的通信系统中用来传送信息的信息率远大于信源极限熵。

为了能够得到或接近信源熵的最小信息率，必须解决编码的问题，而编码分为信源编码和信道编码，其中的信源编码又分为无失真信源编码和限失真信源编码。

由于无失真信源编码只适用于离散信源，所以本次作业讨论无失真离散信源的三种简单编码，即香农（Shannon）编码、费诺(Fano) 编码和哈夫曼(Huffman) 编码[3]。

信息论基础与应用-李梅-第五章 无失真信源编码解析

信息论基础与应用-李梅-第五章 无失真信源编码解析
s1 s1s1 s 2 s1s2 s3 s1s3 s16 s4 s4
二次扩展码码字 w j ( j 1, 2,...,16)
w1 w1w1 00 w 2 w1w2 001 w3 w1w3 0001 w16 w4 w4 111111
第五章：无失真信源编码
一、信源编码的相关概念
4. 关于编码的一些术语

编码器输出的码符号序列 wi称为码字；长度 li 称为码 字长度，简称码长；全体码字的集合C称为码。 若码符号集合为X={0,1}，则所得的码字都是二元序 列，称为二元码。

将信源符号集中的每个信源符号
si 固定的映射成某
一个码字 wi ，这样的码称为分组码。
码字与信源符号一一对应
2) 不同的信源符号序列对应不同的码字序列
第五章：无失真信源编码
一、信源编码的相关概念
6. 唯一可译性（续2）
例1：
1) 奇异码
s1 s2 s3 s4
0 11 00 Байду номын сангаас1
译码 11
s2 s4
奇异码一定不是唯一可译码
第五章：无失真信源编码
一、信源编码的相关概念
6. 唯一可译性（续3）
译码 0 0 0 1 1 0 1 1
s1s2 s3 s4
第五章：无失真信源编码
一、信源编码的相关概念
6. 唯一可译性（续5）
4)
唯一可译码 1 1 0 1 0 0 1 0 0 0 0
s1 s2
1 10
1 0
1
s2 / s3 ?
s3 100 s4 1000

为非即时码
第五章：无失真信源编码
一、信源编码的相关概念

信息论基础与编码— 无失真信源编码ch05.article

信息论基础与编码— 无失真信源编码ch05.article

信息论基础与编码—无失真信源编码Contents1 无失真信源编码基本概念12 定长无失真信源编码23 渐进等同分割性54 定长无失真信源编码定理65 变长无失真编码85.1 Kraft 不等式 (8)5.2 唯一可译码判决准则. . . . . . . . . . . . . . . . . . . . . . . . . 96 变长无失真信源编码定理107 无失真信源编码技术117.1Huffman 编码 (12)7.2Shannon 编码 (12)7.3Shannon-Fano-Elias 编码 (12)7.4Fano 编码 (12)7.5Huffman 编码的几个问题 (13)7.6 算数编码. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 147.7 游程编码. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 157.8 通用编码. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 157.9 几种编码方案的性能对比. . . . . . . . . . . . . . . . . . . . . . . 22 1 无失真信源编码基本概念•对于信源来说有两个基本问题：如何计算信源输出的信息量；如何有效地表示信源输出，即在不失真或允许一定失真的条件下，如何用尽可能少的符号来表示信源，以便提高信息传输的效率。

•编码实质上是对信源的原始符号按照一定的数学规则进行的一种变换。

1, . . . , W q }S : {s Array✻X : {x1, x2, . . . , x r }Figure 1: 信源编码器模型•将信源符号集合中的s i（或者长为N的信源符号序列）变换成由x j 组成的长度为l i 的一一对应的码符号序列W i。

信息论课件第五章_无失真信源编码

信息论课件第五章_无失真信源编码

由此可见,当考虑信源符号之间依赖关系后,有 些信源符号序列不会出现,这样信源符号序列 个数会减少,再进行编码时,所需平均码长就可 以缩短. 英文 等长编码定理给出了信源进行等长编码所需 码长的理论极限值.
5.3 渐进等分割性和ε典型序列
渐进等分割性AEP是弱大数定理的直接推论 大数定理：若X1,X2,…，Xn是独立同分布的随机变 1 量，只要n足够大， ∑ X接近于数学期望E(X)。 n
α i (i = 1,..., q N ) 现在需要把这些长为N的信源符号序列
变换成长度为l的码符号序列 Wi = ( xi1 xi2 ...xil ), ( xi1 ,..., xil ∈ X )
根据前面的分析,若要求得编得的等长码是惟一 可译码则必须满足
qN ≤ rl (5.2)
此式表明,只有当l长的码符号序列数(rl)大于或 等于N次扩展信源的符号数(qN)时,才可能存在等 长非奇异码. 对式(5.2)两边取对数,则有
例如，表5.1中码１是惟一可译码，而码２是 非惟一可译码。 因为对于码２，其有限长的码符号序列能译 成不同的信源符号序列。如：0010,可译成 s1s2s1或s3s1,显然不是惟一的。 下面，我们分别讨论等长码和变长码的最佳 编码问题，也就是是否存在一种惟一可译编 码方法，使平均每个信源符号所需的码符号 最短。也就是无失真信源压缩的极限值。
sik ∈ S ( k = 1, 2,..., N ) xik ∈ X ( k = 1, 2,..., li )
这种码符号序列Wi，称为码字。长度li称为码字长 度或简称码长。所有这些码字的集合C称为码（或 称码书）此码为r元码或称r进制码。
编码就是从信源符号到码符号的一种映射 若要实现无失真编码，必须这种映射是一一 对应的、可逆的。

信息论基础第5章无失真信源编码

信息论基础第5章无失真信源编码
进行霍夫曼编码时，应把合并后的概率总是放在 其他相同概率的信源符号之上，以得到码长方差最小 的码。
r 元霍夫曼编码步骤：
1) 验证所给 q 是否满足 q (r 1) r ，若不满足该式，
可以人为地增加 t 个概率为零的符号，满足式
n (r 1) r ，以使最后一步有 r 个信源符号；
2) 取概率最小的 r 个符号合并成一个新符号，并分别用 0， 1，…，(r 1) 给各分支赋值，把这些符号的概率相加作为该新 符号的概率；
上述不等式只是即时码存在的充要条件，而不能作为判别的依据。
需要注意的是，克拉夫特不等式是即时码存在的充要条件，而 不能作为判别的依据。后来麦克米伦（B. McMillan）证明唯一可译 码也满足克拉夫特不等式。这说明在码长选择的条件上，即时码与 唯一可译码是一致的。
【例】 对于二元码，即 r 2 ，如果 q 4 ， L1 2 ， L2 2 ，
原始信源普遍存在剩余度，香农信息论认为信源的剩余度主 要来自两个方面：一是信源符号间的相关性，二是信源符号概率 分布的不均匀性。为了去除信源剩余度，提高信源的信息传输率， 必须对信源进行压缩编码。
目前去除信源符号间相关性的主要方法是预测编码和变换编 码，而去除信源符号概率分布不均匀性的主要方法是统计编码。
《信息论基础》
第5章 无失真信源编码
第 2 章已经讨论了离散信源的信息度量—信源熵， 本章将讨论信源的另一个重要问题：如何对信源的输出 进行适当的编码，才能用尽可能少的码元来表示信源信 息，做到以最大的信息传输率无差错地传输信息呢？即 无失真信源编码，它解决的是通信的有效性问题。
本章将首先介绍信源编码器；然后从理论上阐述无 失真信源编码定理，得出“平均码长的理论极限值就是

第5章_无失真信源编码

第5章_无失真信源编码
l •定理5.3的条件式也可写成： N log r H (S ) l 令：R ' log r 称之为编码信息率。可见，编码信息 N
率大于信源的熵，才能实现无失真编码。
H (S ) H (S ) l R' log r N
为了衡量编码效果，引进
称为编码效率。
H (S )
15
H (S ) H (S ) 最佳编码效率为： ' R H (S )
信源编码理论是信息论的一个重要分支，其理论基础是信源编码的两个定理。
限失真信源编码定理：香农第三定理
是连续信源/模拟信号编码的基础。
信源编码的分类：离散信源编码、连续信源编码和相关信源编码三类。
离散信源编码：独立信源编码，可做到无失真编码；
连续信源编码：独立信源编码，只能做到限失真信源编码； 相关信源编码：非独立信源编码。
q N r l ， 两边取对数得： l log q
l N
N
log r
表示平均每个信源符号所需的码符号个数。
DUT
信息论基础
9
5.2 等长码
例：对英文电报得32个符号进行二元编码，根据上述关系：
log 32 l 5 log 2
我们继续讨论上面得例子，我们已经知道英文的极限 熵是1.4bit,远小于5bit，也就是说，5个二元码符号只携 带1.4bit的信息量，实际上，5个二元符号最多可以携带 5bit信息量。我们可以做到让平均码长缩短，提高信息传 输率
8、唯一可译码：
若码的任意一串有限长的码符号序列只能被唯一的译成 所对应的信源符号序列，则称此码为唯一可译码。
DUT
信息论基础
8
5.2 等长码
若对信源进行等长编码，则必须满足

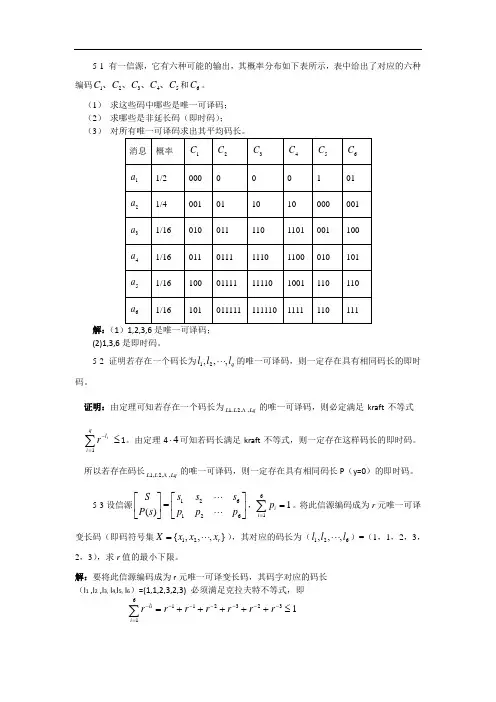
信息论基础与编码(第五章)

信息论基础与编码(第五章)

5-1 有一信源，它有六种可能的输出，其概率分布如下表所示，表中给出了对应的六种编码12345C C C C C 、、、、和6C 。

（1） 求这些码中哪些是唯一可译码； （2） 求哪些是非延长码（即时码）；（3） 对所有唯一可译码求出其平均码长。

解：（1(2)1,3,6是即时码。

5-2证明若存在一个码长为12,,,q l l l ⋅⋅⋅的唯一可译码，则一定存在具有相同码长的即时码。

证明：由定理可知若存在一个码长为的唯一可译码，则必定满足kraft 不等式1。

由定理4可知若码长满足kraft 不等式，则一定存在这样码长的即时码。

所以若存在码长的唯一可译码，则一定存在具有相同码长P （y=0）的即时码。

5-3设信源126126()s s s S p p p P s ⋅⋅⋅⎡⎤⎡⎤=⎢⎥⎢⎥⋅⋅⋅⎣⎦⎣⎦，611i i p ==∑。

将此信源编码成为r 元唯一可译变长码（即码符号集12{,,,}r X x x x =⋅⋅⋅），其对应的码长为（126,,,l l l ⋅⋅⋅）=（1，1，2，3，2，3），求r 值的最小下限。

解：要将此信源编码成为 r 元唯一可译变长码，其码字对应的码长（l 1 ,l 2 ,l 3, l 4,l 5, l 6）=(1,1,2,3,2,3) 必须满足克拉夫特不等式，即132321161≤+++++=------=-∑r r r r r r ri liLq L L ,,2,1 ∑=-qi l ir1≤4⋅Lq L L ,,2,1所以要满足122232≤++r r r ，其中 r 是大于或等于1的正整数。

可见，当r=1时，不能满足Kraft 不等式。

当r=2, 1824222>++，不能满足Kraft 。

当r=3, 127262729232<=++，满足Kraft 。

所以，求得r 的最大值下限值等于3。

5-4设某城市有805门公务电话和60000门居民电话。

作为系统工程师，你需要为这些用户分配电话号码。

信息论基础2012-第五章

信息论基础2012-第五章

简单信源的率失真函数—— Hamming失真度量下的贝努利信源（II）
不妨设p 1 / 2。 1 ）当失真容限D p，则无论信源输出0还是1 ，均可将其编为0， 由此引起的失真不超过p。因此当D p时，R( D ) 0。
2 ）当D p 1 / 2时，有 ˆ ) H(X ) H(X | X ˆ) I(X; X ˆ |X ˆ) H ( p) H ( X X ˆ) H ( p) H ( X X
ˆ) Dmin p( x )Cx p( x ) min d ( x, x ˆ
i 1
0 Di 2 J 1 1 2 Di 2 Di 0 D i
v Di 2
v 2 v 2
1 i2 R( D) log( 2e ) Di i 1 2
m
简单信源的率失真函数—— 平方误差失真度量下的高斯矢量信源（IV）
单符号失真度量是一个映射 ˆ R ˆ) : d ( x, x
失真度量有界是指 ˆ) d max max ˆ d ( x, x
ˆ x x
序列之间的失真度量一般定义为 1 n ˆ ) d ( xi , x ˆi ) d(x , x n i 1 有时也定义为
n n
ˆ n ) max d ( xi , x ˆi ) d ( xn , x
i
失真度量（函数）的重要例子
Hamming 失真 ˆ 0 x x ˆ) d ( x, x ˆ 1 x x
性质： ˆ ) p( x, x ˆ )d ( x, x ˆ) Ed ( X , X
ˆ x,x
R( D )
1 p=0.5
0
0.5
D

(信息论)第5章无失真信源编码

(信息论)第5章无失真信源编码
这就是说，每个英文电报符号至少要用5位二元符号进行 编码才能得到唯一可译码。 12
定长编码定理
定长信源编码定理讨论了编码的有关参数对译 码差错的限制关系
sq p s q
定理 5.3.1 设离散无记忆信源
S s1 P p s 1 p s 2 s2
的熵为H S ，其 N 次扩展信源为
S N 1 p 1 P
2 q p 2 p q

N N

现在用码符号集 X x1 , x2 ,, xr 对N次扩展信源 S N 进行长度为 l 的定长编码，对于 0, 0 ，只要满足
l H S N log r
则当 N 足够大时，译码错误概率为任意小，几乎可以实 现无失真编码。 反之，若满足
l H S 2 N log r
则不可能实现无失真编码。而当N足够大时，译码错误概 14 率近似等于1。

以上的定理5.3.1 和定理5.3.2实际上说明的是一个 问题，虽然该定理是在平稳无记忆离散信源的条件下 证明的，但它也同样适合于平稳有记忆信源，只要要 2 求有记忆信源的极限熵 H S 和极限方差 存在 即可。对于平稳有记忆信源，式(5.6)和式(5.7 ) 中 H S 应该为极限熵 H S 。
变长码(可变长度码)
2
奇异码：若码中所有码字都不相同，则称此码为非
奇异码。反之，称为奇异码。
同价码：每个码符号所占的传输时间都相同的码。定
长码中每个码字的传输时间相同。而变长码中的每个码 字的传输时间不一定相等。
表 5.1
信源符号si
信源符号出现概率 si p

第五章 信道编码

第五章 信道编码

a1 0.5
b1
0.5
a2
0.5
b2
无噪无损信道：错误概率0 P=0.5的二元对称信道：错误概率50%
-信息论基础 李富年 武汉科技大学
信道 编码器
f
译码规则
X
信道
Y
A {a1,a2,.....ar}
B {b1,b2,.....bs}
信道 译码器
F
A {a1,a2,.....ar}
噪声
b1
p(b2 | ar )
p(bs | a1)
p(bs | a2)
p(bs |
ar
)
在这么多种译码规则中，我们选择哪一种?
选择的标准是什么？
当然希望译码后的错误概率越小越好.
-信息论基础 李富年 武汉科技大学
译码规则
对于确定 b j ，制定译码函数 F(bj) ai 译码正确的概率是 p(ai|bj)p [F (bj)|bj] 译码错误的概率是
-信息论基础 李富年 武汉科技大学
b1
b2
F F
(b1 ) (b2 )
a2 a1
错误概率下降为0.01
译码规则
对于一个 rs的传递矩阵，译码规则共有 r s 种
b1
b2
bs
a1 p(b1 | a1)
a2 p(b1 | a2)
ar
p(b1 |
ar
)
p(b2 | a1) p(b2 | a2)
F (b j)a i j 1 ,2 K s
b1
a1 p(b1 | a1) a2 p(b1 | a2)
ar
p(b1 |
ar
)
信息论基础 李富年 武汉科技大学
b2

信息论-无失真信源编码-信源编码

信息论-无失真信源编码-信源编码

码符号集
{b1,L br}
信源编码器（3）
原信源的N次扩展码：
将N个信源符号编成一个码字。相当于对原信 源的N次扩展源的信源符号进行编码。
§信§离单2散源击.2.平1此编1.稳处1自有码添记自条加信器忆标信件息信（题和息自源3的互信）熵信息息
例
信源X={0,1}的二次扩展源X2的 符号集为：{00,01,10,11}。对 X2编码，即为原信源X的二次扩 展码。
1 （01） 1 （1）
分组码（10）
一些结论
r 在码树中，n阶节点的个数最多为 n
例：2进码树中，r阶节点数目最多为 2r
非奇异码字总能与码树建立一一对应的关系
定长码
1.无失真编码条件 2.信源序列分组定理 3.定长码信源编码定理
无失真编码条件（1）
对于定长码, 只要非奇异就唯一可译。这就要求码字的数 目不少于被编码的信源序列的个数 单信源符号编码：
北京邮电大学信息论
第5章
无失真信源编码
Source coding theorem
• Example 2: Suppose that we have a horse race with eight horses taking part. Assume that the (p1ro, 1b,a1b, i1lit,ie1s,o1f w, 1in,n1in)g for the eight horses are
NG 2 N ( H ( X ) )
信源序列分组定理(10)
利用概率估计的上界 1 NG max p(x) NG 2N[H ( X ) ]
x
NG (1 )2N[H ( X ) ]
(1 )2N [H ( X ) ] NG 2N [H ( X ) ]

信息论基础与应用-李梅-第五章 无失真信源编码资料

信息论基础与应用-李梅-第五章 无失真信源编码资料
p(s2)=1/4 p(s3)=1/8 p(s4)=1/8
00
01 10 11
0
01 001 111
第五章：无失真信源编码
一、信源编码的相关概念
3. N次扩展码
S s1 , s2 ,, sq


siBiblioteka C {w1 , w2 ,
, wq }
wi
S s1 , s2 ,
N

, sqN

s jN
计匹配编码，根据信源的不同概率分布而选用与之相 匹配的码。
第五章：无失真信源编码
一、信源编码的相关概念
1. 信源编码概述（续2）

信源的统计剩余度主要决定于以下两个因素 ： 1）无记忆信源中，符号概率分布的非均匀性； 2）有记忆信源中，符号间的相关性及符号概率分布 的非均匀性。

怎样压缩信源的冗余度？
C N {w1 , w 2 ,, w q N }
w j w j1 w j2 w jN
s j s j1 s j2
j 1,2,, q N
j1 , j2 ,, jN 1,2,, q
第五章：无失真信源编码
一、信源编码的相关概念
3. N次扩展码（续1）
二次扩展信源符号 s j ( j 1, 2,...,16)
若一个码中所有码字的码长都相等，则称为定长码；
否则为变长码。
第五章：无失真信源编码
一、信源编码的相关概念
5. 奇异性
若一个码中所有码字互不相同，则称为非奇异码； 否则为奇异码。
信源符号si 码1 码2
s1 s2 s3 s4
0 11 00 11
0 10 00 01
第五章：无失真信源编码

第五章 无失真信源编码定理

第五章 无失真信源编码定理
则不可能实现无失真编码。
第三节 等长信源编码定理
•定理5.3的条件式可写为：
长为l 的码符号所能 载荷的最大信息量 长为N的序列平均携带的信息量
l log r > NH ( S )
只要码字传输的信息量大于信源序列携带的 信息量，总可以实现无失真编码。 l •定理5.3的条件式也可写成： log r H ( S ) e N
i
N
1
2
N
是一一对应的：
i Bi (Wi1 ,Wi2 , ,WiN ), i S ,Wil C
N
4）惟一可译码 若任意一串有限长的码符号序列只能被惟 一地译成所对应的信源符号序列，则此码称 为惟一可译码（或称单义可译码）；否则就 称为非惟一可译码或非单义可译码。
例：对于二元码 C1 {1, 01, 00} ，当任意给定一串 码字序列，例如“10001101”，只可唯一地划 分为1,00,01,1,01，因此是惟一可译码；而对 另一个二元码 C 2 {0,10, 01} ，当码字序列为 “01001”时，可划分为0,10,01或01,0,01，所 以是非惟一可译的。
P(G eN )
-
(2) 若 i (si1, s i2 ,...,s iN ) GeN，则 2 - N [ H ( s )e ] < P( i ) < 2 - N [ H ( s ) -e ] (3) || GeN || 表示e典型序列集中 e典型序列的个数，则 (1 - )2 N [ H ( s )-e ] <|| GeN ||< 2 N [ H ( s ) e ]
1 N - log P ( si ) 以概率收敛于均值 H ( s ) 熵定义 N i 1 1 N 1 即 - log P ( s i ) - log[ P ( s i ) P ( s 2 ) L P ( s N )] N次扩展信源 N i 1 N 1 - log P ( si s 2 L s N ) H ( S ) 以概率收敛 N 因为 i1 ( si1 si 2 L s i N ) S1 S 2 L S N , (i 1, 2 , L , q N i1 , i2 , L , i N 1, 2 , L , q )

第五章：无失真编码1

第五章：无失真编码1

实际信源举例

对于数字型图像信号，可以采用马氏链模型
1 2 X x 2 N 1

1
2 N 1
1 1
而
为相邻像素之间的相关系数。实际信源举例2）语音信源 可以近似用一个一维随机过程U(ω, t)表示。 严格的讲，它是一个非平稳过程，但是对于 短时段(5-50ms)可认为是平稳的，且某些是 随机噪声（清辅音）而某些时段则呈现周期 性特征（浊音），还有一些短时段是二者的 混合。

无记忆信源


在某些简单的离散平稳信源情况下，信源先后发出 的一个个符号彼此是统计独立的。也就是说信源输 出的随机矢量 X=(X１X２…XＮ）中，各随机变量 Xi (i=1,2,…N) 之间是无依赖的、统计独立的，则 N 维 随机矢量的联合概率分布满足 P(X)=P １（Ｘ １） P２ （Ｘ２）…PＮ（ＸＮ） 我们称由信源空间［X，P(x)］描述的信源X为离散 无记忆信源。这信源在不同时刻发出的符号之间是 无依赖的，彼此统计独立的。
可能取值。
离散序列信源

例：最简单 L=3 的三位 PCM 信源：这时 L=3, n=2, 即i={0,1}，则有：
U 3 U 000, U 001,, U 111 3 2 3 p(u ) p , p p , p 0 0 1 1

离散序列信源总结
离散无记忆信源 离散序列信源 离散有记忆信源
一般无记忆 平稳无记忆 平稳序列信源 时齐马氏链信源
随机波形信源


更一般地说，实际信源输出的消息常常是时间和取值都是连续的。例如，语音 X(t)、热噪声信号n(t)、电视图像信号X(x0,y0,t)等时间连续函数。同时， 在某一固定时间t０，它们的可能取值又是连续的和随机的。对于这种信源输出 的消息，可用随机过程来描述。称这类信源为随机波形信源。 分析一般随机波形信源比较复杂和困难。常见的随机波形信源输出的消息是时 间上或频率上为有限的随机过程。根据取样定理，只要是时间上或频率上受限 的随机过程，都可以把随机过程用一系列时间(或频率)域上离散的取样值来表 示，而每个取样值都是连续型随机变量。这样，就可把随机过程转换成时间(或 频率)上离散的随机序列来处理。甚至在某种条件下可以转换成随机变量间统计 独立的随机序列。如果随机过程是平稳的随机过程，时间离散化后可转换成平 稳的随机序列。这样，随机波形信源可以转换成连续平稳信源来处理。若再对 每个取样值(连续型的)经过分层(量化)，就可将连续的取值转换成有限的或可数

信息论第5章 无失真信源编码

信息论第5章 无失真信源编码
若码长l1, l2, …, lq 不满足Kraft不等式à 不是惟一可译码；反之， l1, l2, …, lq 满 足Kraft不等式的码，不一定是惟一可译码。 结论：不能用克拉夫特不等式，只能根据定义 判断码C是否是惟一可译码。 判别依据：非惟一可译变长码 有限长的码 符号序列能译成两种不同的码字序列。
66
香农第一定理的物理意义
无失真信源编码的实质：对离散信源进行变换 变换后信源符号(信道的输入信源)尽可能为等概 率分布 新信源符号平均所含的信息量达到最大 à 使信道的信息传输率R达到信道容量C，实现 信源与信道理想的统计匹配。 无失真信源编码定理通常又称为无噪信道编码定 理。表述为：若信道的信息传输率R不大于信道 容量C，总能对信源的输出进行适当的编码，使 得在无噪无损信道上能无差错地以最大信息传输 率C传输信息，但要使信道的信息传输率R大于C 而无差错地传输信息则是不可能的。
62
63
64
65
定理4.8（香农信息论的主要定理之一）的结论：
要做到无失真的信源编码，编码每个信源符号平均所 需最少的r元码元数为信源的熵Hr(S) 。即Hr(S) 是无 失真信源压缩的极限值。 若编码的平均码长小于信源的熵值Hr(S) ，则惟一可 译码不存在，在译码或反变换时必然要带来失真或差 错。 通过对扩展信源进行变长编码，当N ∞时，平均码长 Hr(S) 。
4
几个术语： 信源符号：信源输入S={s1,s2,…,sq} 码符号 (码元)：X={x1,x2,…,xr} 码字Wi： 由xj (j=1,2,…,r)组成的长度为 li 的序列，Wi与si一一对应。 码字长度 (码长)： Wi的长度li 码 (码书)：码字Wi的集合 C={W1,W2,…,Wq} 编码器：将信源符号si变换成Wi的设备
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

【例】 离散无记忆信源:
U P
u1 0.5
u2 0.25
u3 0.125
u4 0.125
对应的霍夫曼编码？
说明：
霍夫曼编码方法得到的码并非唯一。
每次对信源缩减时，赋予信源最后的两个概率最小的符号， 用0和1是可以任意的，所以可以得到不同的霍夫曼码， 但是不会影响码字的长度。
对信源进行缩减时，两个概率最小的符号合并后的概率与 其他信源符号的概率相同时，这两者在缩减信源中进行概 率排序，其位置放置次序是可以任意的，故会得到不同的 霍夫曼码。这时将影响各码字的长度，但是平均码长相同。 一般将合并后的概率放在上面，这样可以获得较小的码方 差。
本节主要介绍对无记忆离散信源进行的统计编码。统计编码 通常采用变长码。将介绍几பைடு நூலகம்常见的变长码，即香农编码、费诺 编码、霍夫曼编码、算术码和 LZ 码。
【例】 已知信源共 6 个符号，其概率空间为
S
Ps
s1 0.2
s2 0.19
s3 0.18
s4 0.17
s5 0.15
s6 0.11
试进行香农编码。
原始信源普遍存在剩余度，香农信息论认为信源的剩余度主 要来自两个方面：一是信源符号间的相关性，二是信源符号概率 分布的不均匀性。为了去除信源剩余度，提高信源的信息传输率， 必须对信源进行压缩编码。
目前去除信源符号间相关性的主要方法是预测编码和变换编 码，而去除信源符号概率分布不均匀性的主要方法是统计编码。
《信息论基础》
5.1 信源编码的基本概念
几个术语
①码元（码符号） ②码元集X ③码字（由码元组成） ④码字长度 ⑤平均码长
码树还可以用来对即时码进行译码。例如 0 1
收到一串码字 100110010。从码树的树根出发， W1 0 1
第一个码符号为 1，向右走一节；第二个码符号
W2
三位 101 作为 s 的代码。
香农编码是依据香农第一编码定理而来的，有着重要的理 论意义。但香农编码的冗余度稍大，实用性不强。比如信源有 3 个符号，概率分布为（0.5，0.4，0.1），根据香农编码方法求出 各个符号的码长对应为 1，2，4，码字为（0，10，1110）。下面 将看到如果采用霍夫曼编码，可以构造出平均码长更短的即时 码（0，10，11）。
信源熵 Hr S ”这个结论；最后给出几种无失真信源编
码方法。
本章的主要内容
5.1 信源编码的基本概念 5.1.1 信源编码的数学模型 5.1.2 信源编码的分类 5.1.3 唯一可译码和即时码 5.1.4 编码效率
5.2 无失真信源编码定理 5.3 常见的无失真信源编码方法
5.3.1 香农（Shannon）码 5.3.2 霍夫曼（Huffman）码 5.3.3 费诺（Fano）码
解： 以消息 s5 为例来介绍。计算 log( p5 ) log 0.15 2.74 ，
取整数 L5 3 作为 s5 的码长。计算 s1, s2, s3, s4 的累积分布函数
4
F5 Psk 0.2 0.19 0.18 0.17 0.74 k 1
将 0.74 变换成二进制小数 (0.74)10 (0.1011110)2 ，取小数点后面
编码效率: 衡量信源编码的效果.
1．平均码长
2．编码后信道的信息传输率 R
3．编码效率
《信息论基础》
5.2 无失真信源编码定理
当二元编码时（r = 2）
编码器容许的输出信息率
编码效率
R L LN N
H(S)
L
《信息论基础》
5.3 常见的无失真信源编码方法
L3 2 ， L4 2 ，是否存在这样的唯一可译码和即时码？
q
解：因为 2Li 22 22 22 22 1 i 1
所以满足克拉夫特不等式，则一定可以构成至少一种具有这样码长 的唯一可译码和即时码。
在 1956 年，麦克米伦（B. McMillan）证明唯一可译码也满足该不等 式。这说明唯一可译码在码长的选择上并不比即时码有什么更宽松的条 件。在码长选择的条件上，两者是一致的。如前所述，即时码必定是唯 一可译码，它可以很容易地用码树法来构造，因此要构造唯一可译码， 只需讨论构造即时码即可。
定理 5.1 对于码长分别为 L1, L2, , Lq 的 r 元码，若此码为即时码，
则必定满足
q
r Li 1
i 1
反之，若码长满足上式，则一定存在具有这种码长的 r 元即时码。 克拉夫特（Kraft）不等式是即时码存在的充要条件。其中，r 为码元
的进制数，q 为信源的符号数，Li 为信源符号对应的码字长度。注意的是，
上述不等式只是即时码存在的充要条件，而不能作为判别的依据。
需要注意的是，克拉夫特不等式是即时码存在的充要条件，而 不能作为判别的依据。后来麦克米伦（B. McMillan）证明唯一可译 码也满足克拉夫特不等式。这说明在码长选择的条件上，即时码与 唯一可译码是一致的。
【例】 对于二元码，即 r 2 ，如果 q 4 ， L1 2 ， L2 2 ，
0
1
为 0，向左走一节，遇到了码字 W2 。然后再回
W3
W4
到树根，从头开始，遇到了码字后又回到树根。
这样就可完成对即时码的即时译码。码字
100110010 译码得到的码字分别为 W2 10 ，
W1 0 ， W3 110 ， W1 0 ， W2 10 。
对较简单的信源，可以很方便地用码树法直观地构造出即时码。但是 当信源较复杂时，直接画码树就比较复杂。1949 年 L. G. Kraft 提出一个 在数学上与码树等效的、表达即时码存在充要条件的不等式。
【例 5.1】 对四进制信源符号 s1 、s2 、s3 和 s4 采用二元码进行信源编码。
(1) 如果 L1 2 ， L2 2 ， L3 2 ， L4 2 ，是否存在这样码长的二
元即时码？
(2) 如果将此信源编码为 r 元唯一可译码，对应的码长 L1 1，L2 2 ，
L3 2 ， L4 3 ，求 r 值的最佳下限。
《信息论基础》
第5章 无失真信源编码
第 2 章已经讨论了离散信源的信息度量—信源熵， 本章将讨论信源的另一个重要问题：如何对信源的输出 进行适当的编码，才能用尽可能少的码元来表示信源信 息，做到以最大的信息传输率无差错地传输信息呢？即 无失真信源编码，它解决的是通信的有效性问题。
本章将首先介绍信源编码器；然后从理论上阐述无 失真信源编码定理，得出“平均码长的理论极限值就是