第5章 无失真信源编码定理
- 格式:ppt
- 大小:779.00 KB
- 文档页数:9




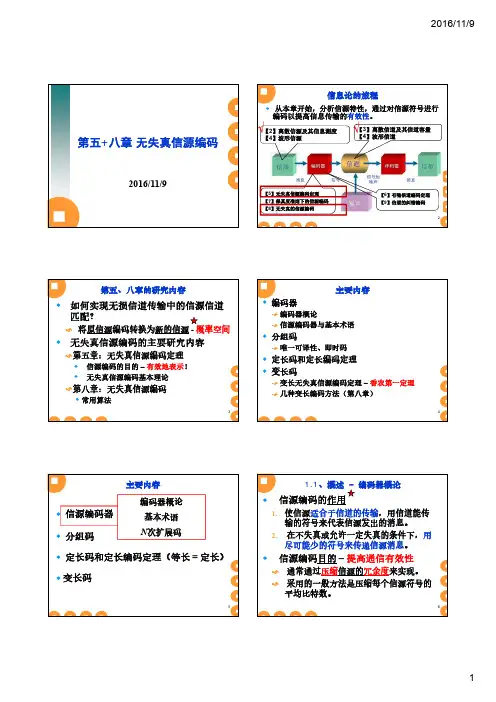
【5】无失真信源编码定理【7】保真度准则下的信源编码【8】无失真的信源编码【6】有噪信道编码定理【9】信道的纠错编码271.1、概述–编码器概论(续)✹信源编码理论是信息论的一个重要分支,其理论基础:无失真信源编码定理;限失真信源编码定理。
✹本章主要介绍无失真信源编码,它实质上是一种统计匹配编码,根据信源的不同概率分布而选用与之相匹配的码。
✹信源的统计剩余度主要决定于以下两个因素无记忆信源中,符号概率分布的非均匀性。
有记忆信源中,符号间的相关性及符号概率分布的非均匀性。
81.1、概述–信源编码器模型✹信源编码:将信源符号序列按一定的数学规律映射成码符号序列的过程。
信宿信道信源编码器译码器X ’XSS ’信源编码器模型{}qs s s S ,,,21 =12{,,,}r X x x x = 91.1、概述–信源编码器模型(续)✹将信源符号集中的符号(或者长为N 的信源符号序列)映射成由码符号组成的长度为的一一对应的码符号序列。
{}q W W W C ,,,21 =编码器},...,,{:21r x x x X {}q s s s S ,,,21 ={}ili i i i x x x W 21=i x i s il i W 101.2、概述–基本术语{}q W W W C ,,,21 =编码器},...,,{:21r x x x X {}q s s s S ,,,21 ={}il i i i i x x x W 21=信源符号集码符号集码字码元/ 码符号代码组C / 码Cr 元码定长码、变长码;奇异码、非奇异码平均码长()∑=ii i l s p L 11信源符号出现概率码字码1码2码3S 1p (S 1)W 10000S 2p (S 2)W 2010111S 3p (S 3)W 31000100S 4p (S 4)W 411111111.2、概述–基本术语–例题5.1()()()()⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡43214321s p s p s p s p s s s s P S 例题:设有二元信道的信源编码器,其概率空间如右:定长码:变长码:非奇异码:奇异码:码1码2、码3码1、码2码3121.3、概述–N 次扩展码✹实际接收:N 次无记忆扩展信源--〉N 次扩展码{}q W W W C ,,,21 ={}qs s s S ,,,21 =is {}12,,,NN q S ααα= },,,{21N q N C W W W =12Nj j j js s s α= Nq j ,,2,1 =qj j j N ,,2,1,,,21 =iW Nj j j j W W W 21=W131.3、概述–N 次扩展码✹例题5.1 -续()16,,2,1 =j j W 00111==W W W 001212==W W W 二次扩展信源符号二次扩展码码字(1,2, (16)j j α=111s s α=212s s α=313s s α=1644s s α=0001313==W W W 1111114416==W W W 信源符号码字码2S 1W 10S 2W 201S 3W 3001S 4W 411114✹信源编码器✹分组码✹定长码和定长编码定理✹变长码主要内容定义唯一可译性即时码的判别与构造152.1、分组码✹分组码:将信源符号集中的每个信源符号映射成一个固定的码字。





第5章无失真信源编码定理●通信的实质是信息的传输。
高效率、高质量地传送信息又是信息传输的基本问题。
●信源信息通过信道传送给信宿,需要解决两个问题:第一,在不失真或允许一定失真条件下,如何用尽可能少的符号来传送信源信息,以提高信息传输率。
第二,在信道受干扰的情况下,如何增强信号的抗干扰能力,提高信息传输的可靠性同时又使得信息传输率最大。
●为了解决以上两个问题,引入了信源编码和信道编码。
●提高抗干扰能力(降低失真或错误概率)往往是增加剩余度以降低信息传输率为代价的;反之,要提高信息传输率往往通过压缩信源的剩余度来实现,常常又会使抗干扰能力减弱。
●上面两者是有矛盾的,然而在信息论的编码定理中,已从理论上证明,至少存在某种最佳的编码或信息处理方法,能够解决上述矛盾,做到既可靠又有效地传输信息。
●第5章着重讨论对离散信源进行无失真信源编码的要求、方法及理论极限,得出极为重要的极限定理——香农第一定理。
5.1编码器●编码实质上是对信源的原始符号按一定的数学规则进行的一种变换。
●图5.1就是一个编码器,它的输入是信源符号集S={s 1,s 2,…,s q }。
同时存在另一符号集X={x 1,x 2, …,x r },一般元素x j 是适合信道传输的,称为码符号(或称为码元)。
编码器是将信源符号集中的符号s i (或者长为N 的信源符号序列a i )变换成由x j(j=1,2, …,r )组成的长度为l i的一一对应序列。
●这种码符号序列W i 称为码字。
长度l i称为码字长度或简称码长。
所有这些码字的集合C 称为码。
●编码就是从信源符号到码符号的一种映射,若要实现无失真编码,必须这种映射是一一对应的、可逆的。
编码器S :{s 1,s 2,…s q }X :{x 1,x 2,…x r }C :{w 1,w 2,…w q }(w i 是由l i 个x j (x j 属于X ))组成的序列,并于s i 一一对应一些码的定义●二元码:若码符号集为X={0,1},所得码字都是一些二元序列,则称为二元码。
第五章 无失真信源编码在第二章与第三章,我们给出了计算信源信息量的方法,在这一章,我们要讲 如何用二进制符号(当然也可采用别的方式)来表示各个信源符号(这个过程 叫信源编码)。
在这个过程中,我们要思考的问题主要是:如何给出一种好的信源编码方法? 我们要解决这样两个问题:1:从理论上来讲,信源编码的编码效率最好能好到什么程度?2:从设计算法的角度来讲,如何使得你的编码算法的效率非常接近最佳的编码效率? 首先我们要谈谈评价信源编码好坏的标准:一:编码的正确性 一个好的信源编码方法首先必须是正确的。
也就是说, 当信宿接收到信源发出的经过信源编码的信息后,它能正确地译码成 信源符号。
为了保证能正确译码,在编码时必须让一个信源符号或 多个信源符号构成的串对应的二进制符号串是唯一的(我们把这种编码 称为唯一可译码)。
唯一可译码要满足什么条件呢?设一个信源符号在信源编码时称为一个码字,首先唯一可译码要求任何两个不同 的信源符号在信源编码时不能用同一个码字表示:如下面的四种编码方法中,码1c 就不是一种唯一可译码。
因为在码1c 中,2s 与4s 的编码都为11,这样信宿就不知道该把11翻译成4s 还是2s (我们把码1c 这种编码方法称为奇异码)。
那么是否所有的非奇异码都是唯一可译的呢?不一定,因为在对某些非奇异码进行译码时我们无法确定一串二进制符号 对应的是一个码字还是多个码字。
如对于码2c 来说,00既可以翻译成11s s ,也可翻译成3s ,所以码2c 还不是唯一可译码。
我们的结论是:若对于任意有限的整数N ,其N 阶扩展码均为非奇 异的,则是唯一可译码。
二:译码的效率高低在编码时不仅要考虑能否正确译码,还要考虑译码的速度是否很快。
讲个例子说明这个问题。
上面的码3c 与码4c 都是唯一可译码,但两种码在译码的时候效率是不一样的。
对于码3c 来说,当信宿接收到符号1时,它不能马上对1进行译码,它必须 等接收到1后面的符号再译码,若1后的符号是1,则可把前一个1翻译成1s ;若1后的符号是0,则信宿也不能马上对10进行译码。