电源的输出功率和外电阻的关系

电功率与电阻的关系在日常生活中，电力是我们不可或缺的能源之一。

而电功率和电阻是电力的重要概念，二者之间存在着密切的关系。

本文将探讨电功率与电阻之间的关系，并从不同角度展开讨论。

一、电功率和电阻的定义和计算公式首先，我们需要了解电功率和电阻的定义。

电功率是指单位时间内电流所做的功，通常用P表示，单位是瓦特(W)。

计算电功率的公式为：P=VI，其中V表示电压，I表示电流。

而电阻是电流通过时所遭遇的阻碍，通常用R表示，单位是欧姆(Ω)。

根据欧姆定律，我们可以得到电阻的计算公式：R=V/I，其中V表示电压，I表示电流。

由上述公式可以得知，电功率和电阻之间的关系是通过电压和电流来联系起来的。

当电阻一定时，电流越大，电压越高，电功率也相应增大。

反之，当电流较小或电压较低时，电功率也会减小。

二、电阻对电功率的影响在电路中，电阻的大小对电功率有着直接的影响。

我们可以通过一个简单的实例来说明这个关系。

假设有两个灯泡，一个电阻较大，一个电阻较小，接在相同电压的电路上。

根据电阻计算公式，电阻越大，电流越小。

而根据电功率计算公式，电阻越大，电功率越小。

因此，电阻较大的灯泡亮度较低，电功率消耗较小；而电阻较小的灯泡亮度较高，电功率消耗较大。

由此可见，电阻的大小直接决定了电功率的大小，较大的电阻会使电功率减小，较小的电阻则会使电功率增大。

这也告诉我们，在设计电路时，我们可以通过调整电阻的大小来控制电功率的消耗。

三、电功率对电阻的影响除了电阻对电功率的影响外，电功率也会对电阻产生一定的影响。

为了理解这个影响，我们可以考虑电阻导致的电能损耗。

根据“热效应”可以得知，电阻在电流通过时会产生热量。

这个热量是因为电子在电阻中受到碰撞而转化成的。

电能损耗会使电阻发热，进而影响电阻的工作状态。

对于电阻较小的情况，由于电流大，电能损耗也相对较大，这会导致电阻升温，可能引起电阻过载，烧坏电路甚至引发火灾等危险。

因此，在设计电路时需要合理选择电阻的阻值以确保电路的安全运行。

电路中的电阻与电功率的关系在电路中，电阻和电功率之间存在着密切的关系。

本文将探讨电阻与电功率的相关性，并通过实例和分析来说明它们之间的联系。

1. 电阻与电功率的基础概念电阻是指电路中对电流流动的阻碍程度，用符号R表示，单位是欧姆（Ω）。

而电功率是指电能转化为其他形式能量的速率，用符号P表示，单位是瓦特（W）。

2. 电阻对电功率的影响在电路中，电阻对电功率的影响是显著的。

根据电功率的定义，P= V * I，其中V表示电压，I表示电流。

根据欧姆定律，电流I = V / R。

将电流的表达式代入电功率的公式中，可以得到P = V^2 / R。

这个公式表明，电功率与电阻呈反比关系。

3. 电阻对电路效率的影响除了影响电功率外，电阻还会对电路的效率产生影响。

电路的效率定义为输出功率与输入功率之比。

当电阻增加时，电流减小，从而减小了输出功率，导致电路的效率下降。

因此，在设计电路时，需要合理选择适当的电阻值，以提高电路的效率。

4. 实例分析：灯泡电路为了更好地理解电阻与电功率的关系，我们可以以一个简单的灯泡电路为例进行分析。

假设有一个12V的电压源和一个5Ω的灯泡。

根据公式P = V^2 / R，可以计算出该电路中的电功率为12^2 / 5 = 28.8W。

为了进一步说明电阻对电功率的影响，我们分别改变灯泡的电阻值。

假设将电阻调节为10Ω，代入公式计算得到电功率为12^2 / 10 = 14.4W。

可以看到，增加电阻导致电功率减小。

同样地，如果将电阻调整为2Ω，代入公式计算得到电功率为12^2 / 2 = 72W。

可以看到，减小电阻导致电功率增加。

5. 总结通过以上实例分析，可以明确电阻与电功率之间的关系：电阻增加会导致电功率减小，电阻减小会导致电功率增加。

这个关系可以通过公式P = V^2 / R来表达。

电路中的电阻与电功率的关系对于电路设计和能源利用具有重要意义。

合理选择电阻值，可以提高电路的效率，减少能源的浪费。

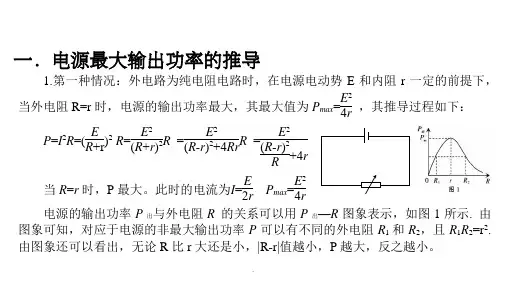
电源输出功率与外电阻的关系————————————————————————————————作者：————————————————————————————————日期：电源输出功率与外电阻的关系一、电源的最大输出功率在电源负载为纯电阻时，电源的输出功率与外电阻R的关系是：P出=I2R=.r4 R)rR(ERr4)rR(RE)rR(RE222222+-=+-=+由此式可以看出，当外电阻等于内电阻（即R=r）时，电源输出功率最大，最大输出功率为r4EP2m=. 电源的输出功率P出与外电阻R 的关系可以用P出—R图象表示，如图1所示. 由图象可知，对应于电源的非最大输出功率P 可以有不同的外电阻R1和R2，且R1R2=r2（请同学们自己证明）. 由图象还可以看出，当R<r时，若R增大，则P出增大；当R>r时，若R增大，则P出减小.注意：1. 推导此关系式时，R是可变电阻，r是定值电阻. 当外电阻等于内电阻，即R=r 时，电源输出功率最大，最大输出功率为r4EP2m=；若R与r不相等，则R值越接近r的值，P出越大.2. 电源的输出功率与电源的效率是完全不同的物理量. 电源的效率Rr11rRR)rR(IRI22+=+=+=η，所以当R增大时，效率η提高. 当R=r时，电源有最大输出功率，但效率仅为50％，效率并不高.二、电源的外特性曲线如图2所示，在电源的外特性曲线上某点纵坐标和横坐标值的乘积为电源的输出功率，图中阴影矩形的面积表示电源的输出功率，当2EU=时，电源输出功率最大. （请同学们想一想，为什么？）例1、如图3所示，电源的电动势E=2V ，内阻r=1Ω，定值电阻R 0=2Ω，变阻器R 的阻值变化范围为0~10Ω，求：（1）变阻器R 的阻值为多大时，R 0消耗的功率最大？（2）变阻器R 的阻值为多大时，R 上消耗的功率最大？是多少？ （3）变阻器R 的阻值为多大时，电源的输出功率最大？是多少？解析（1）R 0消耗的功率020R U P =，由于R 0是定值电阻，故R 0两端的电压越大，R0消耗的功率P 0越大. 而路端电压随着外电阻的增大而增大，所以当R=10Ω时，R 0消耗的功率最大.（2）可以把电源和定值电阻R 0合起来看作一个等效电源，等效电路图如图4所示，等效电源的电动势E ′=V 34V 2122E rR R 00=⨯+=+，等效内阻r ′=Ω=Ω+⨯=+321221r R rR 00，当R=r ′时，即32R =Ω时R 上消耗的功率最大，.W 32W 324)34(r 4E P 22max R =⨯=''=（3）当外电路电阻与内电路电阻相等时，电源输出功率最大，即rR R RR P 00=+=外时，代入数值得：R=2Ω时，电源输出功率最大. 最大输出功率.W 1W 142r 4E P 22max =⨯==例2、如图5所示的电路中，当电键K 断开和闭合时，电源的输出功率完全相同. 已知R 1=9Ω，R 2=7.2Ω，求当K 断开时R 1上消耗的功率P 和K 闭合时R 1上消耗的功率P 1之比.解析：K 闭合时，R 1、R 2并联，其并联电阻为=+=212112R R R R R 4Ω，由于当电键K 断开和闭合时，电源的输出功率完全相同，据2121r R R =可得==121R R r 6Ω，所以有：当K 断开时R 1上消耗的功率21)r R E(P +=·225E 9R 21=；当K 闭合时R 1上消耗的功率925E 4R )R rR E(P 21212121⨯=⋅+=，所以有：.49P P 1=3、（2005江苏物理卷）如图所示，R 为电阻箱，○V 为理想电压表．当电阻箱读数为R 1=2Ω时，电压表读数为U 1=4V ；当电阻箱读数为R 2=5Ω时，电压表读数为U 2=5V ．求：(1)电源的电动势E 和内阻r 。

电源输出功率与外电阻的关系一、电源的最大输出功率在电源负载为纯电阻时，电源的输出功率与外电阻R的关系是：P出=I2R=.r4R)rR(ERr4)rR(RE)rR(RE222222+-=+-=+由此式可以看出，当外电阻等于内电阻（即R=r）时，电源输出功率最大，最大输出功率为r4EP2m=. 电源的输出功率P出与外电阻R 的关系可以用P出—R图象表示，如图1所示. 由图象可知，对应于电源的非最大输出功率P 可以有不同的外电阻R1和R2，且R1R2=r2（请同学们自己证明）. 由图象还可以看出，当R<r时，若R增大，则P出增大；当R>r时，若R增大，则P出减小.注意：1. 推导此关系式时，R是可变电阻，r是定值电阻. 当外电阻等于内电阻，即R=r 时，电源输出功率最大，最大输出功率为r4EP2m=；若R与r不相等，则R值越接近r的值，P出越大.2. 电源的输出功率与电源的效率是完全不同的物理量. 电源的效率Rr11rRR)rR(IRI22+=+=+=η，所以当R增大时，效率η提高. 当R=r时，电源有最大输出功率，但效率仅为50％，效率并不高.二、电源的外特性曲线如图2所示，在电源的外特性曲线上某点纵坐标和横坐标值的乘积为电源的输出功率，图中阴影矩形的面积表示电源的输出功率，当2EU=时，电源输出功率最大. （请同学们想一想，为什么？）例1、如图3所示，电源的电动势E=2V ，内阻r=1Ω，定值电阻R 0=2Ω，变阻器R 的阻值变化范围为0~10Ω，求：（1）变阻器R 的阻值为多大时，R 0消耗的功率最大？（2）变阻器R 的阻值为多大时，R 上消耗的功率最大？是多少？ （3）变阻器R 的阻值为多大时，电源的输出功率最大？是多少？解析（1）R 0消耗的功率020R U P =，由于R 0是定值电阻，故R 0两端的电压越大，R 0消耗的功率P 0越大. 而路端电压随着外电阻的增大而增大，所以当R=10Ω时，R 0消耗的功率最大.（2）可以把电源和定值电阻R 0合起来看作一个等效电源，等效电路图如图4所示，等效电源的电动势E ′=V 34V 2122E rR R 00=⨯+=+，等效内阻r ′=Ω=Ω+⨯=+321221r R rR 00，当R=r ′时，即32R =Ω时R 上消耗的功率最大，.W 32W 324)34(r 4E P 22max R =⨯=''=（3）当外电路电阻与内电路电阻相等时，电源输出功率最大，即rR R RR P 00=+=外时，代入数值得：R=2Ω时，电源输出功率最大. 最大输出功率.W 1W 142r 4E P 22max =⨯==例2、如图5所示的电路中，当电键K 断开和闭合时，电源的输出功率完全相同. 已知R 1=9Ω，R 2=7.2Ω，求当K 断开时R 1上消耗的功率P 和K 闭合时R 1上消耗的功率P 1之比.解析：K 闭合时，R 1、R 2并联，其并联电阻为=+=212112R R R R R 4Ω，由于当电键K 断开和闭合时，电源的输出功率完全相同，据2121r R R =可得==121R R r 6Ω，所以有：当K 断开时R 1上消耗的功率21)r R E(P +=·225E 9R 21=；当K 闭合时R 1上消耗的功率925E 4R )R rR E(P 21212121⨯=⋅+=，所以有：.49P P 1=3、（2005江苏物理卷）如图所示，R 为电阻箱，○V 为理想电压表．当电阻箱读数为R 1=2Ω时，电压表读数为U 1=4V ；当电阻箱读数为R 2=5Ω时，电压表读数为U 2=5V ．求：(1)电源的电动势E 和内阻r 。

等效电源法的应用探讨等效法是从效果相同出发来研究物理现象和物理过程的一种方法，是将一个复杂的物理现象和过程转化为理想的、等效的、简单的物理现象和过程来研究处理。

等效电源法在高中物理学习中是容易被师生忽视的一种解题方法，现就其运用的基本思路与方法作一探讨。

一、等效电源电动势与内阻计算方法根据教材知，电源的电动势应等于开路时的路端电压或可用一理想伏特表直接接在电源两端，便可测量。

如图1、图2，将R 1或R 2视为电源内部，即将虚线框内电路视为等效电源。

由上述结论知图1中，等效电源电动势： E /=E内阻（由于R 1与r 是串联关系）：r /=R 1+r图2中，等效电源电动势：rR ER U E AB +==22/ 内阻（由于R 2与r 是并联关系）：22/R r r R r += 二、电源的特性曲线（即路端电压与总电流的变化关系）电源的电动势和内阻一定时，则路U 与总I 图线为一倾斜直线，图线与纵轴（路U ）的交点表示电源电动势，图线斜率的绝对值表示电源内阻，可见直线完全由电源电动势与内阻决定，故称为电源特性曲线。

上述图2中，原电源、等效电源的特性曲线如图3、图4所示。

三、电源的输出功率与外电阻变化关系设电源电动势为E ，内阻为r ，外电阻为可变电阻R （如图5），试讨论电源输出功率与外电阻的变化关系 ()r R r R E R r R E I U P 4222+-=⎪⎪⎭⎫ ⎝⎛+=•=外外外外总路输由上式可知：①、当R=r 时，输P 最大，即rE P 42max = ②、输P 与R 的函数关系可利用图6定性表述四、等效电源法的应用1、求可变电阻的最大功率例1 如图8电源电动势为E ，内阻为r ，定值电阻R 0，可变电阻R X 可在0--2 R 0之间变化，求R x 消耗的最大功率等效电源法：将图中虚线框内电路视为等效电源，其电动势r R ER E +=00/ 内阻00/R r r R r += R x 消耗的功率 由电源的输出功率与外电阻变化关系可知，当00/R r r R r R x +==，R x 消耗的功率最大，即 2、定性分析可变电阻消耗的功率的变化情况例2 如图9所示电路中1R r 〈，当可变电阻R 3的阻值增大时，A 、电阻R 1两端的电压减少B 、电源输出功率增大C 、电阻R 3消耗的功率减少D 、通过电阻R 3的电流不变不少学生易错选C 答案。

电源的输出功率及有关的几个重要推论摘要：通过对电源输出功率问题的分析研究，总结出比较实用的电源的输出功率及有关的几个重要推论，以便快速准确解题。

关键词：电源输出功率；等效电源；等效内阻；重要推论电源的输出功率问题是高频出现于各类试卷中的典型题目.现就电源的输出功率及有关的几个重要推论简要探讨其后，以便进一步理解和快速解答此类问题.一、电源输出功率的变化规律探讨 1.对于如图1所示的纯电阻电路，电源电动势E ，内阻为r ，当滑动变阻器R 的滑片移动时，试分析电源的输出功率P 出如何变化？因P 出＝I 2R ＝E 2R (R ＋r )2＝E 2(R －r )2R ＋4r .则电源的输出功率P 出随R 的变化规律大致如图2曲线所示，即：①当R ＝r 时，电源的输出功率最大为P m ＝E 24r ．②当R >r 时，随着R 的增大输出功率越来越小．③当R <r 时，随着R 的增大输出功率越来越大． 针对电源的最大输出功率，由R ＝r 和欧姆定律知：④当端电压2E U =时，电源的输出功率最大为P m ＝E 24r ，⑤当总电流rE I 2=时，电源的输出功率最大为P m ＝E 24r .2.对于图3所示的电路等，可结合等效电源法用上述推论快速解答问题.即当R 2= r ′（r ′为等效内阻，即r ′＝R 1+r ）时，滑动变阻器R 2消耗的功率最大，且P 2m =rE '42…特别说明：上述推论成立有条件的，即电路为纯电阻电路，且内阻及等效内阻必须为定值电阻.典例1. 如图3所示的电路，已知电源电动势E ＝5 V ，内阻＝2 Ω，定值电阻R 1＝0.5 Ω，滑动变阻器R 2的阻值范围为0～10 Ω.求：(1)当滑动变阻器R 2的阻值为多大时，电阻R 1消耗的功率最大？最大功率是多少？ (2)当滑动变阻器的阻值为多大时，滑动变阻器消耗的功率最大？最大功率是多少？ (3)当滑动变阻器的阻值为多大时，电源的输出功率最大？最大功率是多少？ 解析：(1)定值电阻R 1消耗的电功率为P 1＝I 2R 1＝E 2R 1(R 1＋R 2＋r )2，可见当滑动变阻器的阻值R 2＝0时，R 1消耗的功率最大，最大功率为P 1m ＝E 2R 1(R 1＋r )2＝2 W.· E r SR P 图1 图2图3(2)将定值电阻R 1看做电源内阻的一部分，则等效电源的等效内阻r ′＝R 1＋r ＝2.5 Ω，等效电动势仍为E ，故当滑动变阻器的阻值R 2＝r′＝2.5 Ω时，滑动变阻器消耗的功率最大，最大功率为P 2m ＝E 24r ′＝)(412r R E +=2.5 W.(3)由电源的输出功率与外电阻的关系可知，当R 1＋R 2＝r ，即R 2＝r －R 1＝(2－0.5) Ω＝1.5 Ω时，电源有最大输出功率，最大功率为P m ＝E 24r ＝3.125 W.二、电源输出功率非最大时的电阻、电流和电压的变化规律探讨当P 出<P m 时，每个输出功率P 对应两个外电阻R 1和R 2，两个电流I 1和I 2，两个外电压U 1和U 2，它们的关系如下：①由Ｐ＝I 2R =R rR E 2)(+，即222Pr Pr)2(+--R E PR ＝０ ，分别设两个根为R 1、R 2，整理得：r PE R R 2221-=+ 和221r R R =. ②由I Ir E UI P )(-==整理得，02=+-P EI rI ，由韦达定理等得：rEI I =+21和r P I I =21．③ 由UI P ==rU E U)(- 整理得，0Pr 2=+-EU U ，由韦达定理等得：E U U =+21和Pr 21=U U典例２.如图４甲所示电路中，R 为电阻箱，电源的电动势为E ，内阻为r ．图乙为电源的输出功率P 与电流表示数I 的关系图象，其中功率P 0分别对应电流I 1、I 2，外电阻R 1、R 2．下列说法中正确的是（ ）A ．I 1+I 2＞rE B.r EI I =+21 BC ．rR 1＞2R r D ．r R 1=2R r解析：由闭合电路欧姆定律得：U =E ﹣Ir ，则输出功率为：P =UI =EI ﹣I 2r ，故有，整理得：rEI I =+21，故A 错误，B 正确； 图４根据电功率表达式，P 0==，且rR EI +=，则有：；整理得：221r R R =，则C 错误、D 正确,；故答案为BD ．巩固练习：1.在纯电阻电路中，当用一个固定的电源(E 、r 是定值)向变化的外电阻供电时，关于电源的输出功率P 随外电阻R 变化的规律如图5所示，则( )A ．当R ＝r 时，电源有最大的输出功率B ．电源有最大的输出功率时电源的效率η＝100%C ．电源的总功率P ′随外电阻R 的增大而增大D ．电源的输出功率P 随外电阻R 的增大而增大2．某同学将一直流电源的总功率P E 、输出功率P R 和电源内部的发热功率P r 随电流I 变化的图线画在同一坐标系内，如图6所示，根据图线可知( )A ．反映P r 变化的图线是bB ．电源电动势为8 VC ．电源内阻为2 ΩD ．电源的最大输出功率为2W3. 将阻值相等的R 1和R 2串联后接在一个稳压电源上，两个电阻均是用金属丝绕制而成的，设R 1温度不变，对R 2加热或冷却，则关于R 2的电功率变化情况，下列说法正确的是( )A. 加热变大，冷却变小B. 加热变小，冷却变大C. 加热、冷却都变小D. 加热、冷却都变大4. 在一些电路中，我们常可以将一部分含电源的未知电路等效成一个不知内阻和电动势的电源.如图7所示，电路虚线框内的各元件参数未知但均为定值，当它的输出端a 、b 间分别接入不同阻值的电阻R x 时，电流表有不同读数I ，则（1）表格中①、②的数值应为（ ） A ．①＝28Ω②＝0.1A B ．①＝38Ω②＝0.2A C ．①＝48Ω②＝0.3A D ．①＝58Ω②＝0.4A（2）R x 为多大时其消耗的功率最大？最大功率为多少？ （3）与10Ω电阻消耗功率相等的另一电阻阻值是多大？5. 如图8所示电路中，R 为电阻箱，电源的电动势为E ，内阻为r 。

电路中的电功率与电阻的关系电路是电子设备中不可或缺的一部分，而电功率和电阻则是电路中的两个重要概念。

电功率是指电路中能量转换的速率，而电阻则是电路中阻碍电流流动的物理量。

本文将探讨电路中的电功率与电阻之间的关系，以及它们对电路性能的影响。

一、电功率的定义和计算方法电功率是指单位时间内电路中能量转换的速率。

在直流电路中，电功率可以通过以下公式计算：P = V × I，其中P表示电功率，V表示电压，I表示电流。

这个公式说明了电功率与电压和电流之间的关系。

当电压或电流增大时，电功率也会相应增大。

二、电功率与电阻的关系电阻是电路中阻碍电流流动的物理量。

根据欧姆定律，电流与电压和电阻之间的关系可以表示为I = V / R，其中I表示电流，V表示电压，R表示电阻。

将这个公式代入电功率的计算公式，可以得到P = V × I = V × (V / R) = V^2 / R。

由此可见，电功率与电阻呈反比关系。

当电阻增大时，电功率会减小，反之亦然。

三、电功率对电路性能的影响电功率的大小直接影响电路的性能。

当电功率过大时，电路中的元件可能会过热，甚至损坏。

因此，在设计电路时，需要根据电功率的大小选择合适的电阻和其他元件，以确保电路的正常运行和安全性。

另外，电功率的大小也与电路的能效有关。

能效是指电路中输入的能量与输出的能量之间的比例。

在理想情况下，电路的能效应该尽可能高，即输出功率接近输入功率。

然而，由于电路中存在电阻，会有一部分能量被转化为热能而损失掉，从而降低了电路的能效。

因此，在实际应用中，需要尽量减小电阻，以提高电路的能效。

四、电阻对电路性能的影响电阻的大小直接影响电路中的电流流动情况。

根据欧姆定律，电流与电压和电阻之间呈反比关系。

当电阻增大时，电流减小；反之，当电阻减小时，电流增大。

因此，通过调节电阻的大小，可以控制电路中的电流大小，从而实现对电路的控制。

此外，电阻还会产生热量。

什么是电流的电功率和电阻之间的关系电流的电功率和电阻之间存在一定的关系。

电功率是指单位时间内电能转化和传输的能力，通常用符号P表示，单位为瓦特（W）。

而电阻是指电流在电路中流动时遇到的阻碍，通常用符号R表示，单位为欧姆（Ω）。

根据电路中电压、电流和电阻之间的关系，可以得出电功率与电流和电阻的关系公式：P = I^2 * R其中P表示电功率，I表示电流，R表示电阻。

从上述公式可以看出，电功率正比于电流的平方，反比于电阻。

当电流增大时，电功率也会增大；当电阻增大时，电功率减小。

具体地说，当电流通过电阻时，会产生耗散能量，也就是电阻的阻力将电能转化为热能。

这时电流的电功率表示电流在电路中传输和消耗的功率。

当电流增大时，单位时间内通过电阻传输的电能增多，因此电功率也会增大。

另一方面，电阻的大小决定了电流流经电路时所遇到的阻碍程度。

当电阻增大时，单位电流通过电路时所需的电压也会增大，因此电功率减小。

这是因为根据功率公式P=VI，电压和电流是成正比的，而电功率与电压的平方成正比。

举个例子来说，假设有一台电灯，其额定功率为50W，接入220V 电源。

根据功率公式可以推导出电流的大小为：P = VI50W = 220V * II ≈ 0.227A这意味着电灯的电流约为0.227安培。

如果电阻发生变化，比如增加了一个外部电阻，那么根据电功率公式可以得出以下结论：P = I^2 * R如果电阻增加，而电流保持不变，那么电功率会减小，电灯的亮度也会降低。

反之亦然，如果电阻减小，电功率会增加，电灯的亮度也会增加。

综上所述，电流的电功率与电阻之间呈现一种相互关系。

电流增大时，电功率也随之增大；电阻增大时，电功率减小。

了解电流的电功率和电阻之间的关系，有助于我们更好地理解电路的工作原理和电能转化过程。