MSR(11)-统计分析-1

格式：ppt
大小：1.19 MB
文档页数：67

下载文档原格式

心理统计学公式总结

心理统计学公式总结一、集中量 1.算术平均数：X??X X??fXNNNi ?n1)2fmd?2.中位数：Md?Lmd?(3.众数：M??3Md?2X4.加权算术平均数：XW?5.几何平均数：Xg?6.调和平均数：XH?二、差异量 1.四分差：QD?N?WX ?W X1X2?XN N1?XQ3?Q1 2 2X?X?2.平均差：MD?N3.标准差：?X?? N24.方差：?2X? ?N5.差异系数：CV??XX100% 6.百分等级分数：PR??Fb???f(X?Lb)?100?N i?7.标准分数：Z? X?X?X 三、相关量1.积差相关系数：r??XY?nXY n?x?y6?D2n(n2?1) 2.斯皮尔曼等级相关系数：rR?1?2?23.肯德尔和谐系数：rW? 式中：SSR??R? 123nK(n?n)12SSR4.点二列相关系数：rpb?Xp?Xq?tpq 5.二列相关系数：rb?Xp?Xqpq ?tY6.多系列相关系数：rs??[(Y?Y)X] (Y?Y)??pLH2LHt7.四分相关系数：rt?cos(180?bc1?ad) 8.Φ相关系数：r??ad?bc(a?b)(a?c)(b?d)(c?d) 9.列联相关系数：c? 四、推断统计?2 N??2XXn?X1.二项分布概率：P?Cpq n2.二项分布平均数：??np 3.二项分布标准差：??npq Ne12??(X??)22?24.正态分布曲线：Y??2? 5.标准正态分布曲线：Y?e?Z22 6.平均数抽样分布标准误：?X??n??Xn?1 五、总体平均数的显著性检验 1.?已知：Z?X??? nX??2.?未知但n＞30：Z??X n?1 3.?未知但n≤30：t?X???Xn?1 六、平均数差异的显著性检验 1.相关大样本：Z?X1?X2?2X1??2X2 ?2r?X1?X2n?1 df?n?1 2.相关小样本：t?X1?X2?2X1??2X2?2r?X1?X2n?13.独立大样本：Z?X1?X2?2X1n14.独立小样本：t???2X2n2X1?X22X2n1??n2?n1?n2?22X1?n1?n2 n1n2 df?n1?n2?2 七、方差齐性检验2n1?X11.两个独立样本：F?(n1?1)(n2?1)2X2n2?2X2df1?n1?1 df2?n2?1 2.两个相关样本：t?22?X??1X24??(1?r)n?22X12df?n?2 八、方差分析 1.完全随机设计：F?MSbSSbSSw组间方差：MSb?组内方差：MSw? MSwdfbdfwSSt?SSb?SSw总平方和：???(X?X)(??X)???X??n2t2总自度：dft?dfb?dfw 2SSb?n?(Xj?Xt)组间平方和：22(??X)2 组间自度：dfb?K?1 ???n?nSSw???(X?Xj)2组内平方和：???X??22组内自度：df??n?K bn2.随机区组设计：处理水平差异显著性检验：F?MSbSSbSSe 组间方差：MSb? 误差方差：MSe? MSedfbdfe区组差异显著性检验：F?SSeMSrSSr区组方差：MSr? 误差方差：MSe? MSedfrdfeSSt?SSb?SSr?SSe总平方和：???X?2(??X)2总自度：dft?nK?1 nK组间平方和：SSb??2n(?R)2K?(??X)2nK(??R)2nK 组间自度：dfb?K?1 区组平方和：SSr??? 区组自度：dfr?n?1 误差平方和：SSe?SSt?SSb?SSr 误差自度：dfe?dft?dfb?dfr 3.在F检验拒绝H0后：完全随机设计：q?X1?X2MSw11(?)2n1n2X1?X2MSe11(? )2n1n2 随机区组设计：q?九、总体比率的假设检验?p?p? p?q?n 2.两个独立样本比率差异的显著性检验：Z?p1?p2(n1p1?n2p2)(n1q1?n2q2)n1n2(n1 ?n2)b?cb?c 3.两个相关样本比率差异的显著性检验：Z?十、?2检验21.单项表的?检验：??? 自度：df?K?1 ft b、c为不和谐频数22 2f022.双项表的?检验：????N(??1) 自度：df?(r?1)(c?1) ftnrnc22 2N3.独立样本四格表的?检验：?? 自度：df?1 (a?b)(a?c)(b?d)(c?d)22(b?c)24.相关样本四格表的?检验：?? 自度：df?1 b?c22十一、相关系数的显著性检验 1.积差相关系数的检验：??0且n≥50：Z?rn?1 21?r 自度：df?n?2 ??0且n＜50：t?rn?21?r2???0：Z?n?3 Zr1?Zr211?n1?3n2?3 两个相关系数差异的显著性检验：Z?2.斯皮尔曼等级相关系数的检验：t?rRn?21?r2R 自度：df?n?2 3.肯德尔和谐系数的检验：?2?K(n?1)rw 自度：df?n?1 4.点二列相关系数的检验：t?rpbn?21?rrb2pb 自度：df?n?2 5.二列相关系数的检验：Z?1Ypqn 6.多系列相关系数的检验：t?rs?n?21?rs?2 rs??rs(YL?YH)2?[p] 自度：df?n?2 7.四分相关系数的检验：Z?rt1Y1Y2p1q1p2q2N 228.Φ相关系数的检验：??Nr? 自度：df?(r?1)(c?1) f029.列联相关系数的检验：??N(??1) 自度：df?(r?1)(c?1) nrnc2十一、相关系数的显著性检验 1.积差相关系数的检验：??0且n≥50：Z?rn?1 21?r 自度：df?n?2 ??0且n＜50：t?rn?21?r2???0：Z?n?3 Zr1?Zr211?n1?3n2?3 两个相关系数差异的显著性检验：Z?2.斯皮尔曼等级相关系数的检验：t?rRn?21?r2R 自度：df?n?2 3.肯德尔和谐系数的检验：?2?K(n?1)rw 自度：df?n?1 4.点二列相关系数的检验：t?rpbn?21?rrb2pb 自度：df?n?2 5.二列相关系数的检验：Z?1Ypqn 6.多系列相关系数的检验：t?rs?n?21?rs?2 rs??rs(YL?YH)2?[p] 自度：df?n?2 7.四分相关系数的检验：Z?rt1Y1Y2p1q1p2q2N 228.Φ相关系数的检验：??Nr? 自度：df?(r?1)(c?1) f029.列联相关系数的检验：??N(??1) 自度：df?(r?1)(c?1) nrnc2。

第三章趋势面分析

的回归显著性检验
离差来源
（K+1）次回归（K+1）次剩余
K次回归
K次剩余
由K次增高至
（K+1）次的回归总离差源自平方和SSR(K 1)
SSD(K 1)
SS
(K R
)
SSD(K )
自由度
均方差
F检验
p n–p–1
q n–q–1
MS
(K R
1)
SSR(K !)
/
p
MSD(K 1)
SSD(K !) /(n p 1)
第三章地理学中的经典统计分析方法
第6节趋势面分析方法
➢趋势面分析的用途 ➢趋势面分析的一般原理 ➢趋势面模型的适度检验 ➢趋势面分析应用实例 ➢趋势面分析的软件实现
一、趋势面分析的用途
❖ 趋势面分析(trend surface analysis, TSA)的主要功能是找出研究区域内变量的空间分布格局。描述地理要
二、趋势面分析的一般原理
空间趋势面是一种光滑的数学曲面，它能集中地代表地理数据在大范围内的空间变化趋势。它与实际上的地理曲面不同，它只是实际曲面的一种近似值。趋势面是一种抽象的数学曲面，它抽象并过滤掉了一些局域随机因素的影响，使地理要素的空间分布规律明显化。
实际曲面=趋势面+剩余曲面。趋势面反映了区域性的变化规律，它受大范围的系统性因素影响，属于确定性因素作用的结果。而剩余面反映局部性变化特点，它受局部因素和随机因素的影响。
图3.6.2 某流域降水量的三次多项式趋势面
模型检验
(1)趋势面拟合适度的R2检验: 根据R2检验方法计算，结果表明，二次趋势面的判定系数为R22=0.839，三次趋势面的判定系数为 R32=0.965，可见二次趋势面回归模型和三次趋势面回归模型的显著性都较高，而且三次趋势面较二次趋势面具有更高的拟合程度。

BSC常见故障处理

CDU-A或C型的小区，由于要两根TX/RX天线，若方向角严重不一致，则QD、SD掉话多，质差切换比正常小区多，切入成功率与接通率偏低。
区分方向角不一致造成的影响与直放站的影响要有足够呛的经验，一般方向角不一致要注意QD、SD比例多；而直放站则是SU、QU多；200站及D型较难区分，不过直放站常伴QU掉话。
要注意QD、SD一般较少出现，多与TRU故障或天线偏差、交叉相关。
天线下倾角不一致，有SU掉话略高，质差切换比例大，切入成功率偏低等迹象。
（3）、天线老化
天线老化一般是SU、SUD掉话较多，切入成功率低，接通率低，其迹象与同BCCHNO同BSIC的迹象类似，故较难判定。而是实地测天线，往往VSWR没明显变差，或不稳定，时大时小；故需排除直放站，同BCCHNO同BSIC的可能后做仔细反复的测试。
观察处理：
STS指标上：开跳频时，QD掉话数量相对较多；
关跳频时，SD掉话与QD掉话相对较多；
切换：向外切换时，下行质差紧急切换多；切入城功率较低；接通率低；
路测：强信号质差较严重；200站开跳频后信号质差。
（2）பைடு நூலகம்RX故障：
主要表现：
分集接收故障、接收灵敏度偏低。
观察处理：
ICM统计上：出现有两极分化的上行干扰，即在测试报告中，1级干扰的测量点数有一部分，然后另一部分在3至5级，查告警有CF 2A/33分集接收故障，这类一般都有1到2个载波有故障，用RLCRP配合RXCDP指令可确认具体的故障载波。
（2）、全网各小区各项指标均正常，但总掉话总数与无线掉话总数相差较大，话务量大时更为明显。一般为TRA设备有部分故障。
（3）、小区各项指标均正常，但SDCCH接通率偏低。一般先检查有无同频率组，开跳频又同HSN的小区存在，若如此，试改HSN；如果不存在该类小区，或修改HSN后无效果，一般是TRH的问题。拆小区MO数据重LOAD，一般可觖决问题。

爱华声级计仪器本身的符号及定义

爱华声级计仪器本身的符号及定义爱华声级计仪器本身的符号及定义爱华声级计仪器本身的符号及定义：一、符号、缩写定义Ts 设定的积分测量时间Tm 实际测量经历时间Nm 实际统计分析的采样个数GPS 全球定位系统N: 组名或测点的名称，用户可输入。

H: 24小时自动监测时的当前时间段号24H 24小时自动监测模式STA 单次统计分析模式F 时间计权快档，时间常数为125msS 时间计权慢档，时间常数为1000msI 时间计权脉冲档，上升沿时间常数为35ms，下降沿时间常数为1500msR@ 24小时自动监测时的第一组启动时刻Lpx 传声器灵敏度级LAeq A计权等效声级LCeq C计权等效声级LZeq Z计权等效声级SEL 声暴露级 =Leq+10Log(T)E 个人声暴露，单位为Pa2hLmax 最大声压级Lmin 最小声压级L5 5%的声压级超过此声压级L10 10%的声压级超过此声压级L50 50%的声压级超过此声压级L90 90%的声压级超过此声压级L95 95%的声压级超过此声压级SD 均方偏差LAFp F档测量到的一秒内的最大A声级LASp S档测量到的一秒内的最大A声级LAIp I档测量到的一秒内的最大A声级LA1s 一秒钟的A计权等效声级LCFp F档测量到的一秒内的最大C声级LCSp S档测量到的一秒内的最大C声级 LCIp I档测量到的一秒内的最大C声级LC1s 一秒钟的C计权等效声级LZFp F档测量到的一秒内的最大Z声级LZSp S档测量到的一秒内的最大Z声级LZIp I档测量到的一秒内的最大Z声级LZ1s 一秒钟的Z计权等效声级LAFi F档测量到的瞬时A 声级LASi S档测量到的瞬时A声级LAIi I档测量到的瞬时A声级LCFi F档测量到的瞬时C声级LCSi S档测量到的瞬时C声级LCIi I档测量到的瞬时C声级LZFi F档测量到的瞬时声压级LZSi S档测量到的瞬时声压级LZIi I档测量到的瞬时声压级Ld 昼间等效声级，时间段为6:00到22:00Ln 夜间等效声级，时间段为22:00到6:00Ldn 昼夜间等效声级LCpk 峰值C声级Lat 纬度，以度为单位Lon 经度，以度为单位Alt 海拨Vel 速度SMS 短消息UTC 世界标准时间,比北京时间晚8个小时GMT+8 格林威治时间，与UTC相同，+8表示格林威治时间早8个小时OCT 倍频程频谱分析Rang 量程W_A A计权声压级W_C C计权声压级W_Z Z计权声压级电池电量显示电池欠压有GPS定位信号 SD卡已插入成功发送短消息 90度方向入射爱华声级计仪器本身的符号及定义二、主要性能指标1 传声器：预极化测试电容传声器,灵敏度级：-46dB至-26dB(以1V/Pa为参考0dB)。

统计学简答题

《统计学原理》简答题1、环形图与饼图的区别饼图是用圆形及圆内扇形的面积来表示数值大小的圆形，它主要用于表示总体中各组成部分所占的比例，对于研究结构性问题十分有用。

环形图与饼图类似，但它们之间也有区别。

环形图中间有一个“空洞”，总体或样本中的每一部分数据用环中的一段表示。

而饼图只能显示一个样本（或总体）中各组成部分的数据占全部数据的比例，而环形图则可以同时绘制多个样本（或总体）的数据系列，每一个总体或样本数据系列为一个环。

因此，环形图可显示多个样本各部分所占的相应比例，从而有利于比较研究。

2、直方图与条形图的区别①条形图使用图形的长度表示各类别频数的多少，其宽度固定，直方图用面积表示各组频数，矩形的高度表示每一组的频数或频率，宽度表示组距；②直方图各矩形连续排列，条形图分开排列；③条形图主要展示分类数据，直方图主要展示数值型数据。

3、什么是统计分组？其作用是什么？⑴定义：根据统计研究的目的与任务，将社会经济现象总体按照可变的标志划分为若干组份部分的一种统计方法。

⑵作用：①研究总体的内部结构 ②划分社会经济类型 ③揭示现象之间的依存关系4、什么是统计总体，其基本特征是什么？⑴统计总体：是由客观存在的、在同一性质的基础上结合起来的，许多独立的个别事务的整体。

⑵基本特征：大量性同质性差异性5、统计标志及标志的具体表现⑴统计标志：用来说明总体单位特征的名称⑵具体表现：跟在总体单位特征后面的文字描述或数值表示。

6、统计调查方案的内容包括哪些？①调查目的②调查对象和调查单位③调查项目④调查表⑤调查方式和方法⑥调查地点和调查时间⑦组织计划7、假设检验的步骤①提出假设 ②确定适当的检验统计量 ③规定显著性水平α ④计算检验统计量的值 ⑤做出统计决策8、方差分析中的多重比较——最小显著差异法（LSD ）的具体步骤：第1步：提出假设：H 0：j i μμ=；H 1：j i μμ≠第2步：计算检验统计量：j i x x -。

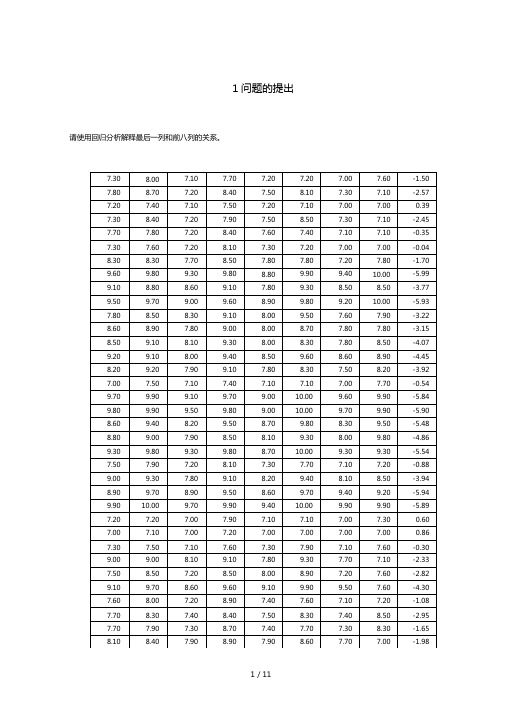
回归分析的应用

1问题的提出请使用回归分析解释最后一列和前八列的关系。

2、模型的准备多元统计分析是运用数理统计方法来研究解决多指标问题的理论和方法。

并通过计算机对相关的数据进行分析得到相应的结果。

本文通过建立多元统计分析方法中的多元回归分析模型并使用SPSS软件来分析数据得到多元回归方程。

2.1多元回归分析原理与模型回归分析是一种处理变量的统计相关关系的一种数理统计方法。

回归分析的基本思想是：虽然自变量和因变量之间没有严格的、确定性的函数关系，但可以设法找出最能代表它们之间关系的数学表达形式。

回归分析主要解决以下几个方面的问题（1）、确定几个特定的变量之间是否存在相关关系，如果存在的话，找出它们之间合适的数学表达式；（2）、根据一个或几个变量的值，预测或控制另一个变量的取值，并且可以知道这种预测或控制能达到什么样的精确度；（3）、进行因素分析。

例如在对于共同影响一个变量的许多变量（因素）之间，找出哪些是重要因素，哪些是次要因素，这些因素之间又有什么关系等等。

多元回归分析是研究多个变量之间关系的回归分析方法，按因变量和自变量的数量对应关系可划分为一个因变量对多个自变量的回归分析（简称为一对多”回归分析）及多个因变量对多个自变量的回归分析（简称为多对多”回归分析）,按回归模型类型可划分为线性回归分析和非线性回归分析。

设随机变量y与m个自变量存在线性关系：；' 门+讥旬+二辽 -------- 匚叫:匕-■（1）（1）式称为回归方程，式中- - 为回归系数，为随机误差。

现在解决用厂.心」亠「…①J估计y的均值「心'的问题,即且假定总冲N（炖+加尽心卫7）氐血"氐庐'是与小匕无关的待定常数。

设有n组样本观测数据：比1也％…止脱丿2也,…，族世其中X j表示X j在第i次的观测值,于是有：用最小二乘法估计参数(m)，使残差平方和h =则“血+如n+・・•+』汕扮+fph =曲+加21+如船+卄携％+仏h 丄血+商心桦2也+・・・+切轴|+L其中心「1*1…丘为m+1个待定参数，•宀'，，，：£?］为n 个相互独立的且服从同一正态分布”匚的随机变量,(2) 式称为多元(吒元)线性回归的数学模型。

利用Rayleigh熵和并行计算的大规模电网异常负荷快速识别

利用Rayleigh熵和并行计算的大规模电网异常负荷快速识别李洪乾; 韩松; 周忠强【期刊名称】《《电力系统保护与控制》》【年(卷),期】2019(047)023【总页数】7页(P37-43)【关键词】大规模电网; MESCM; Rayleigh熵; 并行计算; 异常负荷识别【作者】李洪乾; 韩松; 周忠强【作者单位】贵州大学电气工程学院贵州贵阳 550025【正文语种】中文随着广域测量系统(Wide Area Measurement System, WAMS) 以及智能电网的建设与发展，爆炸式增长的数据量对电网数据处理及知识提取提出了挑战[1-2]。

将大数据思维引入电力系统分析[3-4]，从电力以至相关非电数据中挖掘知识及其价值应用，借助高性能计算技术实现电网运行状态的大数据思维分析与评价[5]，对确保新一代电力系统安全具有重要的理论意义。

随机矩阵理论(Random Matrix Theory, RMT)是一种具有普适性的方法，无需详细物理模型，可以从高维角度认识复杂系统的行为特征。

从基于RMT的电力系统分析理论与方法研究进展来看，文献[6]采用RMT中平均谱半径(Mean Spectral Radius, MSR)作为相关性指标，开展了各种影响因素与配电网运行状态之间的内在联系挖掘研究。

文献[7]综合考虑了电网历史数据和实时数据，基于MSR指标提出了一种电网静态稳定态势评估的方法。

文献[8]进一步利用MSR指标分析电网状态，提出了一种电网扰动定位的方法。

文献[9-10]依据RMT原理提出了一种基于样本协方差矩阵最大特征值(Maximum Eigenvalue of Sample Covariance Matrix, MESCM)的适用于低信噪比场景的电网异常状态识别方法。

然而，上述文献中案例分析大多采用数十个母线的小规模系统算例，尚未对此类方法在大规模电力系统的适应性，如基于全部特征值求解技术的MSR或MESCM指标计算效率不高，全域求解效率偏低等问题开展研究。

08第八章统计分析

（3）随机化：随机区组实验设计要求每一区组必须接受所有种处理，并且在每一区组中接受处理的顺序必须是随机决定的。
（二）随机区组实验设计方差分析的基本程序
• 单因素随机区组实验设计的方差分析将由区组产生的离差平方和从误差离差平方和中分离出来，从而使总离差平方和被分解为三个部分：处理离差平方和 S S b 、区组离差平方和 S S r 与误差离差平方和。
SSeSStSSbSSr
• 自由度分别为：
dfb k 1
dfr a 1
dfe(k1)(a1)
dft N 1
• 均方分别为；
MSb
SSb dfb
SSb k 1
MSr
SSr dfr
SSr a 1
MSe
(k
SSe 1)(a1)
（3）进行F检验：先计算处理均方与误差均方的方差
比：
Fb
M Sb M Se
差一致即方差齐性。否则原则上便不能运用方差分析方法。
二、单因素完全随机化设计的方差分析
• 单因素完全随机化设计指的是用随机化的方法给处
理指派实验序号和实验对象的实验设计。在实验中
仅有一个实验因素，它分处于 k 个水平（k 2 ），
用随机化的方法将N名被试分为 k 组，每组 n j 个对
象，且
k
nj
一、基本原理
（一）综合虚无假设与部分虚无假设
• 虚无假设应为：各样本组所对应的总体其平均数都相等，一般我们把这一假设称为“综合虚无假设” 。而组间的虚无假设相应地就应被称为“部分虚无假设”。检验综合虚无假设是方差分析的首要任务。如果综合虚无假设被拒绝，就要确定究竟是哪两个（或哪些）组之间的平均数之间存在显著性的差异，而这又需要运用事后检验方法来确定。

RSSI问题处理方法总结

1.假设一个三扇区基站的第一扇区的主集和分集相差过大或第一扇区的主分集都过高。
1)上站后首先对馈线接头进行检查，包括1/2馈线与机顶接口处和1/2馈线与7/8馈线接口处是否松动，若发现松动将其拧紧（注意：接头处不要拧得太紧以免将馈线内部的顶针压变形）机房跟踪结果，否则下一步。
2)检查天馈的驻波比，确保从天线到机顶的驻波比符合要求（一般要求驻波比小于1.4），如果驻波比较大，建议整改天馈，直道馈线的驻波比合格，否则进行下一步检查
RSSI问题处理方法总结
RSSI问题处理方法总结福建项目组郑晗目前福建三地已陆续割接完毕，在割接期间和割接后的一段时间中RSSI问题给我们带来了很大的困扰，那么造成RSSI不正常的原因到底是是什么？根据不同的情况该如何有效的处理，在此给大家一些参考希望能对RSSI的整改起到一定帮助。 1.1 RSSI异常现象 RSSI异常可以从以下几个角度体现出来，现场工程师可根据这些现象结合现场的实际情况进行综合判断： 1.用户感觉接入困难，用户平均接入时间较长，一般长于5秒以上；问题严重时，用户根本无法接入系统；语音质量不好，通话断续、有杂音、静音、单通现象，严重时甚至掉话； 2.终端观察到的现象终端发射功率持续偏高，Rx＋Tx>-70dBm以上；终端显示有信号，但是无法拨打电话，经过长时间接入（约20s）后掉网，然后重新搜网； 3.话统现象载频平均RSSI较高（高于－93dBm）； RSSI值过低，长时间低于-113dBm或者固定为-120dBm； RSSI主分集别差异长时间超过5dB； FER过高，接入成功率、软切换成功率低，掉话率高，且接入失败和掉话的原因主要为空口； 4.其他现象：在RFMT跟踪数据中，RevBadFrame、RevSetEbNt、FwdFer、FwdSetEbNt、MsRxPwr 等指标将恶化。目前我们可以通过M2000、Nastar及操作维护台跟踪或Telnet到基站跟踪这几种方式来跟踪RSSI，为了方便大家准确定位 RSSI问题建议大家使用下面这个工具来对RSSI进行分析，通过导入一天或几天的数据对其分析更加全面的定位出RSSI的具体原因，这样才能更准确的指导工程队进行整改。

常用研究模型

定性研究模型1.基于“需求—动机—行为的理论”行为学基础模式的市场行为模型2.波特钻石模型波特认为，决定一个国家的某种产业竞争力的有四个因素：(1) 生产要素――包括人力资源、天然资源、知识资源、资本资源、基础设施；(2) 需求条件――主要是本国市场的需求。

(3)相关产业和支持产业的表现――这些产业和相关上游产业是否有国际竞争力。

(4)企业的战略、结构、竞争对手的表现。

波特认为，这四个要素具有双向作用，形成钻石体系（如下图）。

在四大要素之外还存在两大变数：政府与机会。

机会是无法控制的，政府政策的影响是不可漠视的。

3.SWOT分析模型4.对标管理研究模型5.MOSTER（MO nitoring S atisfaction T o E nsure R etention）满意度模型6.PSM模型介绍：价格敏感度测试模型（Price Sensitive Model）,是目前在价格测试的诸多模型中，最简单、最实用。

通过PSM模型，不仅可以得出最优价格，而且得出合理的价格区间。

获得用户对不同价格的接受能力和接受范围。

7.品牌定位模型：通过分析用户使用产品的决策，找到决策影响因子与选用品牌间的关系，展现品牌竞争对象、品牌定位和品牌优劣势。

模型利用对应分析(Correspondence analysis)，也称关联分析、R-Q型因子分析。

此模型是近年新发展起来的一种多元相依变量统计分析技术，通过分析由定性变定量构成的交互汇总表来揭示变量间的联系。

8.临界消费行为模型9.EGM评价栅格法10.KANO分析模型：这个模型由日本狩野教授和他的同事们提出。

引用在汽车调查中，可以测量某些配置的需求性质，在不同的定位下是否应该提供，以及是否应该作为独特卖点进行宣传。

功能和配置，可以分成以下四类：无差异属性（Indifferent quality ）魅力属性（Attractive quality ）一维属性（One-dimensional quality ）必要属性（Must-be quality ）（1）一维属性：与客户满意度线性相关的属性被称作“一维属性”，这类属性性能的改进将使客户的满意度线性增加。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

一、描述性统计(Descriptive Statistics) 描述性统计
3.平均数平均数
1 X= ∑ X i N
平均数的特点： ▲平均数的特点：它对数值极大或极小的个案特别敏感
一、描述性统计(Descriptive Statistics) 描述性统计
众数： ◆众数：对定名变量是最合适的选择
A B
基尼系数值总是介于0，之间之间， ◆基尼系数值总是介于，1之间，数值越大，表明分配越不均等。表明分配越不均等。
基尼系数的计算--洛论茨曲线法基尼系数的计算洛论茨曲线法：洛论茨曲线 X轴——人口百分比， Y轴——收入百分比。轴人口百分比，轴收入百分比。人口百分比收入百分比收入等级最低20% 最低20% 次低20% 次低20% 中间20% 中间20% 次高20% 次高20% 最高20% 最高20% 占家庭总收入的百分比 6 12 17 24 41 累计占家庭收入百分比 6 18 35 59 100
第十讲统计分析的基本概念与方法（）统计分析的基本概念与方法（1）
一、描述性统计分析二、样本分布三、推断性统计的基本概念四、假设检验五、相关分析六、回归分析
一、描述性统计(Descriptive Statistics) 描述性统计
(一)百分比、相对比与图表一百分比百分比、
1. 百分比百分比(Percentage) 表1.某单位职工婚姻状况分布某单位职工婚姻状况分布婚姻状况单身已婚离婚寡居合计人数 1000 700 200 100 2000 百分比(%) 百分比 50 35 10 5 100
◆中位数：对定序变量是最合适的选择中位数：
平均数； ◆平均数；对定距和定比变量是最合适的选择
一、描述性统计(Descriptive Statistics) 描述性统计
▲虽然变量的集中趋势提供了变量分布的描述,但虽然变量的集中趋势提供了变量分布的描述但仅知其集中趋势是不够的. 仅知其集中趋势是不够的清华附近2家送快餐公司的送餐速度例1:清华附近家送快餐公司的送餐速度清华附近家送快餐公司的送餐速度: A:平均送到家的时间为分钟但最快分钟到最平均送到家的时间为12分钟但最快3分钟到平均送到家的时间为分钟,但最快分钟到,最分钟到; 慢30分钟到分钟到 B:平均送到家的时间为分钟但最快分钟到平均送到家的时间为13分钟但最快10分钟到平均送到家的时间为分钟,但最快分钟到, 最慢15分钟到分钟到. 最慢分钟到 Q:你愿意选哪家你愿意选哪家? 你愿意选哪家 => 还需对变量的离散趋势还需对变量的离散趋势(Dispersion)进行测量进行测量
一、描述性统计(Descriptive Statistics) 描述性统计 2. 变量的平均离散值/平均偏差(Average Deviation) 变量的平均离散值平均偏差
平均离散值:变量中的每一个值与平均数的距离平均离散值变量中的每一个值与平均数的距离之和. 之和 AD = 1 n
∑ xi − x n =
寡居 5% 离婚 10% 单身 50% 已婚 35% 单身已婚离婚寡居
图1.某单位职工婚姻状况分布某单位职工婚姻状况分布
60 50 40 30 20 10 0 单身已婚离婚寡居 10 5 50 35 百分比
图1.某单位职工婚姻状况分布某单位职工婚姻状况分布
120 100 80 60 40 20 0
一、描述性统计(Descriptive Statistics) 描述性统计
◆平均数和标准差把复杂的变量分布概括为
两个数字，两个数字，我们对变量的中心趋势和离散趋势有了一个直观的了解。趋势有了一个直观的了解。
一、描述性统计(Descriptive Statistics) 描述性统计
4. 差异系数差异系数(coefficient of variation) （1）两个或两个以上样本所使用的观测工具不）所测的特质不同；标准差的单位不同，同，所测的特质不同；——标准差的单位不同，标准差的单位不同不能比较。不能比较。例：身高与体重（2）两个或两个以上样本所使用的是同一种观）测工具，所测的特质相同，测工具，所测的特质相同，但样本间的水平相差较大。平均值的大小不同，差较大。——平均值的大小不同，不能比较。平均值的大小不同不能比较。例：时序列或横向数据差异系数=（标准差/平均值平均值）差异系数（标准差平均值）*100%
一、描述性统计(Descriptive Statistics) 描述性统计
◆基尼系数
是描述一组数据的分散程度的另一个相对指标。常用于作为描述不平等的指标。相对指标。常用于作为描述不平等的指标。
20世纪初意大利经济学家基尼．Gini)，根世纪初意大利经济学家基尼(C．世纪初意大利经济学家基尼，据洛伦茨曲线找出了判断分配平等程度的指标（如下图），设实际收入分配曲线和收入分配绝如下图），设实际收入分配曲线和收入分配绝），对平等曲线之间的面积为A，对平等曲线之间的面积为，实际收入分配曲线右下方的面积为B。并以A除以除以A+B的商表示不右下方的面积为。并以除以的商表示不平等程度。平等程度。这个数值被称为基尼系数或称洛伦茨系数。系数。
一、描述性统计(Descriptive Statistics) 描述性统计
(三)变量的离散趋势三变量的离散趋势变量的离散趋势(Dispersion)的测量的测量 1.极差全距极差/全距极差全距(Range) 极差=变量最高值极差变量最高值 – 最低值例1: RA=30 – 3 =27 RB=15 – 10 =5 ▲但极差仅反映了变量最高值和最低值的差异, 但极差仅反映了变量最高值和最低值的差异对变量分布中的其他值未加以考虑(浪费了许对变量分布中的其他值未加以考虑浪费了许多信息) 多信息 => 变量的平均离散值平均偏差变量的平均离散值/平均偏差平均偏差(Average Deviation)
一、描述性统计(Descriptive Statistics) 描述性统计
计算例1的结果按S计算例的结果计算例的结果:
次数 1
2 12
3 7 11
4 3 13
5 10 14
6 13
9 24 14
10 6 14
A B
8
12 10
A公司的平均值分钟公司的平均值:12分钟公司的平均值 B公司的平均值分钟公司的平均值:13分钟公司的平均值 SA=8.74 SB =1.56 公司比A公司的送餐速度稳定的多即你估计B 故B公司比公司的送餐速度稳定的多即你估计公司比公司的送餐速度稳定的多(即你估计公司送餐到你家的时间的误差比A公司小的多公司小的多) 公司送餐到你家的时间的误差比公司小的多
1910 1920 1930 1940 1950 1960 1970 1980 1990 2000
学龄儿童入学
图2. 各年代学龄儿童入学率
一、描述性统计(Descriptive Statistics) 描述性统计
百分比、 ◆百分比、相对比与图表仅仅给出了变量分布的直观信息，布的直观信息，若想对变量分布的特征有更进一步的把握，更进一步的把握，还需对其分布的结构做进一步处理。进一步处理。
◆基尼系数计算公式
对收入分配X=（而言，对收入分配（ x1, x2,… xn ）而言，用每一对x 用每一对 i ,xj的差的绝对值的合计除以收入，来反映不平等的程度。收入，来反映不平等的程度。 1 G(x)= 2n2 µ
∑ ∑| xi -xj |
联合国有关组织规定： ◆联合国有关组织规定：若低于0.2表示收入绝对平均；若低于表示收入绝对平均；0.2-0.3 表示收入绝对平均表示比较平均；表示相对合理；表示比较平均；0.3-0.4表示相对合理；表示相对合理 0.4-0.5表示收入差距较大；0.6以上表示表示收入差距较大；以上表示表示收入差距较大收入差距悬殊。收入差距悬殊。
1 ∑ ( − )2 S = Xi X N
2
一、描述性统计(Descriptive Statistics) 描述性统计
标准差: 标准差
标准差即方差的平方根。
2 1 S = ∑ Xi − X N
(
)
即以平均数来估计变量中每一个值所犯的错误平均该值越大,变量的分布面就越大是S.该值越大变量的分布面就越大它显示变量分该值越大变量的分布面就越大.它显示变量分布的离散程度. 布的离散程度
一、描述性统计(Descriptive Statistics) 描述性统计
(二)变量的集中中心趋势二变量的集中中心趋势(Central tendency) 变量的集中/中心趋势的测量 1.众数（mode）众数（众数） 2.中位数中位数(median) 中位数 3.平均数平均数(mean) 平均数
二、概率分布
1.随机变量随机变量 ◆离散型随机变量如果变量x，其可能取值至多为可列出的若干个，如果变量，其可能取值至多为可列出的若干个，且以各种确定的概率取这些不同的值，则称x为离且以各种确定的概率取这些不同的值，则称x为离散型随机变量 (discrete random variable)。 ) ◆连续型随机变量如果变量x，其可能取值为某范围内的任何数值，如果变量，其可能取值为某范围内的任何数值，在其取值范围内的任一区间中取值时，且x在其取值范围内的任一区间中取值时，其概率在其取值范围内的任一区间中取值时是确定的，则称x为连续型随机变量为连续型随机变量( 是确定的，则称为连续型随机变量(continuous random variable)。 )
i1
一、描述性统计(Descriptive Statistics) 描述性统计