当前位置：文档之家 › 简单几何体表面展开图(课堂PPT)

简单几何体表面展开图(课堂PPT)

  • 格式：ppt
  • 大小：682.50 KB
  • 文档页数：5

下载文档原格式

  / 5

合集下载

《简单几何体的表面展开图》PPT课件 (公开课获奖)2022年浙教版 (6)

《简单几何体的表面展开图》PPT课件 (公开课获奖)2022年浙教版 (6)
合局部忽略不计〕.
S
216°
A
OB
做一做
2. 图3 -3是四个几何体的平面展开图 ,请用纸分别复制下来 ,猜测以下展 开图可折成什么立的形 状.
〔1〕 〔3〕
〔2〕 〔4〕
练习
以下各图是几何体的平面展开图 ,猜测以下展开图可折成 什么立体图形 ,并指出围成的几何体的形状.
_0__.8_x____7_2_;
2、物体在水下 ,水深每增加米承受的压力就会增加1个大气压.
当 "蛟龙〞号下潜至||3500米时 ,它承受的压力约为340个
大气压.问当它承受压力增加到500个大气压时 ,它又继续下潜
了多少米 ?
340 1 x500
设它又继续下潜了x米 ,可列出方程
10.33
3_、_小__强__、_小__杰_、__张_明__参__加_投__篮比赛 ,每人投20次.小强投进10个
球 ,小杰比张明多投进2个 ,三人平均每人投进14个球.问小杰和小
明各投进多少个
2x 12 14
设第|一次射击的成绩为x个 , 可列方程为3
0.8x72
观察你所列的方程 ,这些方
340 1 x500 10.33
程之间有什么共同的特点
★方程两边都是整式；
?
2x 12 14 3
★方程中只含有一个未知数； ★未知数的指数是一次 .
方程的两边都是整式，只含 有一个未知数，并且未知数 的指数是一次，这样的方程 叫做 一元一次方程 。
⒈判断以下各式哪些是一元一次方
程 ? (1)5x =0
√
x (2)y2 =4 +y
√ (3)3m +2 =1 -m
(4)1 +3x

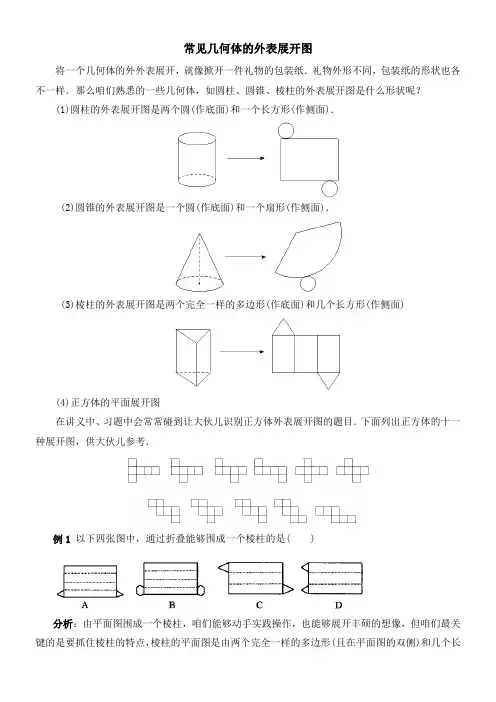
常见几何体的表面展开图

常见几何体的表面展开图

常见几何体的外表展开图将一个几何体的外外表展开，就像掀开一件礼物的包装纸．礼物外形不同，包装纸的形状也各不一样．那么咱们熟悉的一些几何体，如圆柱、圆锥、棱柱的外表展开图是什么形状呢？(1)圆柱的外表展开图是两个圆(作底面)和一个长方形(作侧面)．(2)圆锥的外表展开图是一个圆(作底面)和一个扇形(作侧面)．(3)棱柱的外表展开图是两个完全一样的多边形(作底面)和几个长方形(作侧面)(4)正方体的平面展开图在讲义中、习题中会常常碰到让大伙儿识别正方体外表展开图的题目．下面列出正方体的十一种展开图，供大伙儿参考．例1 以下四张图中，通过折叠能够围成一个棱柱的是( )分析：由平面图围成一个棱柱，咱们能够动手实践操作，也能够展开丰硕的想像，但咱们最关键的是要抓住棱柱的特点，棱柱的平面图是由两个完全一样的多边形(且在平面图的双侧)和几个长方形组成的．解：正确答案选C．点评：专门要注意的是两个完全一样的多边形是棱柱的上下两个底面图形(棱柱展开后，这两个图形是位于展开图的双侧)，故不选D，另外定几个长方形，究竟是几个呢，它的个数确实是上下底多边形的边数，应选C．例2如以下图的平面图形是由哪几种几何体的外表展开的？(1) (2) (3)分析：找几何体的外表展开图，关键是看侧面和底面的形状．底面是圆的几何体有圆柱、圆锥、圆台．侧面是扇形的几何体是圆锥．侧面是长方形的几何体是棱柱、圆柱．解答：(1)圆锥；(2)圆柱；(3)圆台．例3如以下图，在正方体的两个相距最远的极点处停留着一只苍蝇和一只蜘蛛，蜘蛛能够从哪条最短的途径爬到苍蝇处?说明你的理由．分析：在解这道题时，正方体的展开图对解题有专门大的帮忙，由于作展开图有各类不同的方式，因此从蜘蛛到苍蝇能够用6种不同方式选择最短途径，而其中每一条途径都通过连结正方体2个极点的棱的中点．解：由于蜘蛛只能在正方体的外表爬行，因此只需作出那个正方体的展开图并用点标出苍蝇和蜘蛛的位置，依照“两点之间线段最短〞这一常识可知，连结这两个点的线段确实是最短的途径．点评：这种求最短路程是多少及求与棱的夹角是多少等问题，同窗们容易犯的错误是：用棱柱来计算路程，可求出的却不是最短的．通过对该节内容的学习，咱们必然要养成擅长观看，随时寻觅规律的良好适应，只有如此，才能把所学知识融会贯穿．。

简单几何体的表面展开图 PPT课件 3 浙教版

简单几何体的表面展开图 PPT课件 3 浙教版
∴∠BAD = 60°.在RtΔABC中， ∠BAD = 60°, AB = 3.
∴ BD = 3 3 2
答： 解：
它 将 爬圆 行的锥 最短沿 路线A 是B 23 展 3. 开成扇形ABB，
垂足为D.
则点C是BB的中点，
过点B作BD
AC，
BAB r 360 120 l
BAD 60.在RtABC中， BAD 60, AB 3.
5.圣诞节将近, 某家商店正在制作圣诞节的 圆锥形纸帽。已知纸帽的底面周长58cm，高为 20cm，要制作20顶这样的纸帽至少要用多少 平方厘米的纸？（结果精确到0.1cm2）
解：设纸帽的底面半径为rcm，母线长为lcm，
r 58
2
l ( 58 )2 202 22.03(cm)
360
2
如图,圆锥的底面半径为1,母线长为4,一只 蚂蚁要从底面圆周上一点B出发,沿圆锥侧面爬 行一圈再回到点B,问它爬行的最短路线是多少?
A
B
C
解:设圆锥的侧面展开图为扇形ABB’, ∠BAB’=n°
连接BB’,即为蚂蚁爬行的最短路线
∵ 圆锥底面半径为1,母线长为4
∴
2π=
4nπ 180
B’
n=90
例1 如图3-48为一个圆柱的三视图.以相同的比例画出 它的表面展 开图，并计算它的侧面积和全面积(果 保留π).
分析：由图3-48知，圆柱底面圆的半
径r为0.9cm，母线长l 为
2.4 cm. 因此圆柱的表面展 开图中两个底面应画成半 径为0.9cm的圆，侧面展开
图应画成长为2πr=2π×0.9
， l
∴∠BAD = 60°.在RtΔABC中
∠BAD = 60° , AB = 3.

立体图形的展开图ppt课件

立体图形的展开图ppt课件
1
常见平面图形：
三角形
正方形
长方形
平行四边形
菱形
2
圆形 扇形
圆环
椭圆形
3
常见立体图形：
正方体
长方体
4
圆柱体
圆锥体
5
四棱锥
三棱柱
6
三棱台
圆台
球体
7
你认为设计制作一个包装盒 需要了解什么？ 要包装的物体的形状、大小； 它展开后的形状、大小； 材料、美术设计等等。
8
许多立体图形是由一些 平面图形围成的，将它 们适当的剪开，就可以 展开成平面图形．这就 是立体图形的平面展开 图．
21
想一想：图中的几个图形能否折叠 成为棱柱？
（1） （3）
（2）
（4）
22
这些图案分别在 正方体的哪个面 上？23能找出 符合要求 的展开图 吗？
（1）
（2）
（3）
24
（4）
猜猜哪 个才是
左 上后
“我”？ 前 右
上
下 （1）
前
右
前
下 左后
上右 （3）
右 上
后 左前
下 （2）
左
下 前 上后
9
长方体的平面展开图
长方体
10
棱锥的平面展开图
三棱锥
11
圆柱体的平面展开图
圆柱体
12
圆锥体的平面展开图
圆锥体
13
棱台的平面展开图
三棱台
14
圆台的平面展开图
圆台
15
球体是否可以 展成平面图形？ 球体
16
连一连
17
下列图形能折叠成什么图形？
圆柱体 圆锥
五棱柱

几何体的表面展开图(动画演示直观形象)优秀课件

几何体的表面展开图(动画演示直观形象)优秀课件

实验学校初一数学组
26
圆 柱
展开
实验学校初一数学组
27
圆锥
展开
实验学校初一数学组
28
棱柱
展开
实验学校初一数学组
29
长方体
展开
实验学校初一数学组
30
下面4个图是一些多面体的表面展 开图,你能说出这些多面体的名字吗?
正方体
长方体
四棱锥
实验学校初一数学组
三棱柱
31
形展如开有图的，一形上种状面牛？的把奶图它形包们分装用别盒线是连如下起面图来哪所。个示立。体图 为了生产这种包装盒，需要先画
GO SKIP
2
将一个正方体的表面沿某些棱剪开,
能展成哪些平面图形？
友情提示：
可以动手剪,也 可以想着画.
1、沿着棱剪
2、展开后是 一个图形
实验学校初一数学组
3
实验学校初一数学组
4
实验学校初一数学组
5
实验学校初一数学组
6
实验学校初一数学组
7
-
实验学校初一数学组
8
-
实验学校初一数学组
9
巧记正方体的展开图口诀 : 中间四个面上下各一面， 中间三个面一二隔河见 , 中间二个面楼梯天天见 , 中间没有面三三成一线, 其中“凹”“田”不能现，
了！ 太棒 你们
实验学校初一数学组
KEY: 棒
18
规律： 相对两面不相连： 上下隔一行，左右隔一列。 （简称：隔一相对）
实验学校初一数学组
14 1型19
2 3 1型
实验学校初一数学组
20
3 3型
222型
实验学校初一数学组
21

几何体的表面展开图PPT课件

几何体的表面展开图PPT课件

Thank
在别人的演说中思考，在自己的故事里成长
Thinking In Other People‘S Speeches，Growing Up In Your Own Story 讲师：XXXXXX XX年XX月XX日
28
你有何高招？
● 蚊子
壁虎 ●
26
写在最后
经常不断地学习,你就什么都知道。你知道得越多,你就越有力量 Study Constantly, And You Will Know Everything. The More
You Know, The More Powerful You Will Be
27
2
4
5
提示：先想好从哪剪开
6
14
活动二 用剪刀把桌上的正方体纸盒按任意方式沿 棱展开，你能得到哪些不同的展开图？比 比哪一小组的展开图更与众不同。
15
16
第一类，中间四连方，两侧各一 个，共六种。（一四一型）
17
第二类，中间三连方，两侧各有 一、二个，共三种。（二三一型）
18
第三类，中间二连方，两侧各有二 个，只有一种。（二二二型）
第四类，两排各三个，只有一种。 （三三型）
19
试一试
下面六个正方形连在一起的图形，经折 叠后能围成正方体的图形有哪几个？(动手试 试）
A
B
C
D
E
F
G
20
下面的图形是正方体的表面展开图吗?
×
×
×
×
×
√
21
“考考你”活动
1.下图是一个长方体展开图,图中已标出三个 面在正方体中的位置,f表示前面,r表示右面,d表 示上面,你能判断另外三个面a,b,c在正方体中的位 置吗?

立体图形和表面展开图(共11张PPT)

1如果你在档分享小结1立体图形是由平面图形组成的
初中一年级 数学（上）
§4.3 立体图形的展开图
陈伟文
第1页，共11页。
圆柱体 展开 长方形
圆锥体 展开 扇形
第2页，共11页。
第3页，共11页。
一、做做看：
下列三图中哪一个可以折叠成多面体？
(1)Βιβλιοθήκη (2)(3)第4页，共11页。
正方体
长方体
四棱锥
第5页，共11页。
三棱柱
练习：
下列图形中是某些多面体的展开图？
(1)
长方体
(2)
五棱锥
(3)
三棱柱
第6页，共11页。
想一想：
下列的图形都是正方体的展开图吗？
(3)
(1)
(2)
(√)
(√)
(4)
(5)
(√)
(6)
(√)
(×)
第7页，共11页。
第11页，共11页。
下列的图形都是正方体的展开图吗？
1、P139页1、2、3
2、“坚”在下，“就”在后，胜利在哪里？
3 立体图形的展开图 1、P139页1、2、3
胜
是
利
第10页，共11页。
小结
1、立体图形是由平面图形组成的。 2、能根据展开图判断立体图形。 3、能判断平面图形是否为立体图形的展开图。
作业
1、P139页1、2、3 2、制作精美的盒子做为给父母、老师或朋友的元旦礼物。
你们
了 棒
！
KEY: 棒
第9页，共11页。
2、“坚”在下，“就”在后，胜利在哪里？
初中一年级 数学（上）
坚
3 立体图形的展开图
下列图形中是某些多面体的展开图？

3.4简单几何体的表面展开图(2).ppt


变式（二）
如图，圆柱形容器中，高为1.2 m，底面周长为1 m， 在容器内壁离容器底部0.3 m的点B处有一只蚊子
（假设蚊子没有发现壁虎，并且保持不懂），此时
一只壁虎正好在容器外壁，离容器上沿0.3 m与蚊
子相对的点A处，则壁虎吃到蚊子的最短距离为 ________(容器厚度忽略不计)
谈谈你的获……
主视图 左视图
25
10
俯视图
图3-48
①铝皮：
②羊皮：
S侧=ch =6π×2.6
2S底=πr²×2 =3²π×2
=15.6π（dm²）
=18π（dm²）
答：至少需要铝皮15.6π平方分米， 羊皮18π平方分米
已知一个圆柱的表面积为150
cm2,母线长为10cm。求这个圆柱 的底面半径。
你还能设计什 么样的题目？
探究活动
如图,一只蚂蚁在圆柱的底面A处,B处有一滴 蜜，它准备沿着圆柱的侧面爬到B处,它怎样 爬行路线最近？其中圆柱的底面圆周长为 24cm，高为6cm.先说说你的解题思路,然后 给出解答,并算出最近路线的长.
B
AB 62 +122 =6 5
A
变式（一）
有一圆柱形油罐底面圆的周长为24m，高为6m， 一只蚂蚁从距底面1m的A处爬行到对角B处吃蜂 蜜，它爬行的最短路线长为_______
× 等于圆柱的底面直径，宽等于圆柱的高。 （ ）
2、给大厅的圆柱刷油漆，刷油漆的部分面积是圆柱的侧
面积。
（√ ）
3、一个圆柱的侧面展开是正方形，它的底面周长和高
相等。
（√ ）
例1 如图3-48,为一个圆柱的三视图。以相同的
比例画出它的表面展开图，并计算这个圆柱 单位:mm 的侧面积和表面积（结果保留π）
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

甲
乙
丙 10
如图，有一边长4米立方体形的房间，一只蜘蛛在A处，一只 苍蝇在B处。⑴试问，蜘蛛去抓苍蝇需要爬行的最短路程是多少？
⑵若苍蝇在C处，则最短路程是多少？ C”（C）
C
4cm
B
4cm
C’（C）
A
11
C’
如图，有一长方体形的房间，地面
为边长4米的正方形，房间高3米。一
C
只蜘蛛在A处，一只苍蝇在C处。 试问，蜘蛛去抓苍蝇需要爬行的最短
将几何体沿某些棱剪开,并使各个面 连在一起，这样的图形叫几何体的表 面展开图。
口诀
展开图规律之一:立方体的展开过程需要剪七刀.
展开图规律之二: 异层 “日”字连,整体没有“田 ”
“一三二”, “一四一”.
“一”一在四同一层型可任意；
“三个二”成阶梯，
“二个一三三”二，型“日”字连；
异层 “日”字连
5 63 2 1 (5)
5632
(6) 1
563
563
(7) 1 2 (8) 1 2
4
54
563
63
563
(9) 1 2
(10) 1 2
(11)
1
2
4
5
平面“七刀”现; 对面“不相连”; “日”字异层见; 整体没有“田”;
补充: 立方体表面展开图的周长是小正方形边长的14倍.
6
试一试
下面六个正方形连在一起的图形，经折 叠后能围成正方体的图形有哪几个？(动手试 试）
A
B
14
A B
15
探究活动：小组讨论并探究怎样利用
表面展开图和两点间线段最短的原理解
. . 决节前图的著名迷题。
A
A
.A
.B
AB=5
.B
.B
C
AB=5
AB 521.82 5.31
16
一. 平面“七刀”现; 二. 对面“不相连”; “日”字异层见; 整体没有“田”;
17
如图是立方体的表面展开图，要求折成立方体后，使 得6在前，右面是2，哪个面在上？
整体三没个有“二田型”
二个三型
3
立方体相对两个面在其展开图中的位置相连吗?
展开图规律之三: 对面不相连.
5
2 1 34
4
5632 1 (1)
4 5 6 32
1 (2)
4 5632
(3) 1
6
4 56 3 2
(4) 1
4
4
4
4
5 63 2 1 (5)
5632
(6) 1
563
563
(7) 1 2 (8) 1 2
1 2 56
34
18
合作游戏(二) 下面的图形都是立方体的展开图吗？
19
添上一个小正方形,使下图折叠后能围成一个 立方体,共有几种添法？
20
长方体
正方体
三棱柱
21
根据下面几个表面展开图表面展开图吗？
三 棱 柱
甲
乙
丙
23
下面的图形是正方体的平面展开图，如果把
25
它们叠成正方体，哪个字母与哪个字母对应（即 哪个面与哪个面是对面的）
AB CD E F
AB C D EF
24
有一个正方体，在它的各个面上分别写了①、②、 ③、④、⑤、⑥。甲、乙、丙三位同学从三个不同的角 度去观察此正方体，结果如下图，问这个正方体各个面 的对面的是什么数？
⑥ ②④
甲
① ③②
乙
⑤ ④③ 丙
E
B
路程是多少？
A
D
12
---- “蜘蛛和苍蝇”问题 杜登尼(Dudeney,1857-1930年)是19 世纪英国知名的谜题创作者．“蜘蛛 和苍蝇”问题.
A B
13
---- “蜘蛛和苍蝇”问题 在一个长方形长、宽、高 分别为3米，2米，2米长方 体房间内，一蜘蛛在一面的中间，离天花板０.１米 处(A点)，苍蝇在对面墙的中间,离地面0.1米处(B点 ),试问:蜘蛛去捉苍蝇需要爬行的最短距离是多少?
2
c 7 -1 b a
9
合作游戏----争连做连小看小数学家
有如一图种，牛上奶面包的装图盒形如分图别所是示下。面为哪了个生立产体这图种形包展装开的 盒形，状需？要把先它画们出用展线开连图起纸来样。。
（1）如图给出的三种纸样，它们都正确吗？ （2）从已知正确的纸样中选出一种，标注上尺寸； （3）利用你所选的一种纸样，求出包装盒的侧面积 和表面积（侧面积与两个底面积的和）
A
B
C
D
E
F
G
7
如图，这是一个正方体的展开图，如果将它组成原来 的正方体，哪些点与点P重合。
S
T
P
H
R
U
V
M
N
Q
Z
W
K
Y
8
如图是一个正方体纸盒的展开图，图中的6个正 方形中分别已填入了-1、7、 2 、a、b、c，使展开 图沿虚线折叠成正方体后相对面上的两个数互为 相反数,求: a -_ _ _ 2 ,b _ -_ 7_ ,c _ 1_ _ _
4
54
563
63
563
(9) 1 2
(10) 1 2
(11)
1
2
4
4
立方体展开图的周长是每个小正方形边长的几倍?
展开图规律之四: 立方体表面展开图的周长是小 5
正方形边长的14倍.
4
5632 1 (1)
4 5 6 32
1 (2)
4 5632
(3) 1
2 1 34
6
4 56 3 2
(4) 1
4
4
4
4
杜登尼(Dudeney,1857-1930年)是19世纪英国知 名的谜题创作者．“蜘蛛和苍蝇”问题最早出现 在1903年的英国报纸上，它是杜登尼最有名的谜 题之一．它对全世界难题爱好者的挑战，长达四 分之三个世纪．
A B
1
把你们小组所做的立方体纸盒沿着某些棱剪开， 且使六个面连在一起,然后铺平,把你所得到的图形画 出来,数一数剪了几刀?并比一比,有何异同?