浙教版九年级数学下册课件：3.4简单几何体的表面展开图(2)——圆柱的表面展开图(共24张PPT)

分别是圆柱两底面圆周上的点，且 A，B 在同一母线上， 用一棉线从 A 顺着圆柱侧面绕 3 圈到 B，求棉线最短为
________cm.
答案：圆柱体的展开图如图所示：用一棉线从 A 顺着圆柱侧面 绕 3 圈到 B 的运动最短路线是：AC→CD→DB；即在圆柱体的展 开图长方形中，将长方形平均分成 3 个小长方形，A 沿着 3 个
长方形的对角线运动到 B 的路线最短；∵圆柱底面半径为 2cm， ∴长方形的宽即是圆柱体的底面周长：2π×2＝4πcm； 又∵圆柱高为 9πcm，∴小长方形的一条边长是 3πcm； 根据勾股定理求得 AC＝CD＝DB＝5πcm； ∴AC＋CD＋DB＝15πcm.
例 一矩形纸板，两边长分别为 2cm 和 4cm，绕一边所
变式：如果圆柱的两底面积之和等于侧面积，那 么母线与底面直径之比等于________．
答案：1∶2
例 2 有一圆柱形油罐底面圆的周长为 24m，高为 6m，
一只老鼠从距底面 1m Hale Waihona Puke A 处爬行到对角 B 处吃食物，
它爬行的最短路线长为多少？ 解 答案析：：∵由A于C＝老6鼠－是1＝沿5着，圆∴柱BC的＝表24面×爬12＝行12的，，故需把圆 柱 由勾展股开定成理平得面图AB形2＝．AC根2＋据BC两2＝点1之69间，线∴段AB＝最1短3(，m)可．以发
例 1 如图，要用钢板制作一个无盖的圆柱形水
箱，它的高为 2.5m，容积为 10m3.需用钢板多少(不
计加工余量，精确到 0.1m2)? 解析：设水箱底面半径为 r(m)，由水箱的容积为 10m3， 得 2．5×πr2＝10.∴r＝ 2.5×103.14≈1.13(m)．
反圆思柱：侧求面积圆柱S 侧的≈侧2×面3积.1、4×全1.面13积×，2.需5≈要17知.7道4(圆m2柱)．的底 面圆半柱径底和面积母线S 底两≈个3.量14，×可1.1以32根≈据4.体01(积m2求)，出底面半径． S 全≈17.74＋4.01≈21.8(m2)．所以，共需钢板约 21.8m2.

S全
=2πr²+2πrl=2π×0.9²+2π×0.9×2.4
=5.94π (cm²). 答：这个圆柱的侧面积为4.32πcm²，全
面积为5.94πcm².
圆锥的定义：以直角三角形的直角边所在 直线为旋转轴，其余两边旋转而成的曲面 所围成的几何体叫做圆锥。（记作圆锥SO）
S O
轴 侧 面母 线 底 面
圆锥的表面展开图
将圆锥的侧面沿它的一条母线剪开，会得到圆锥的侧面展 开图为扇形，其半径等于母线长，弧长是底面圆的周长．
如图，若圆锥的底面半径为r，母线长为l，则
l2=h2+r2 S侧＝πrl； S表＝S侧＋S底＝πrl＋πr2＝πr(l＋r)．
若设圆锥的侧面展开图扇形的圆心角为θ ，则 r θ ＝ l ·360°.
2
∴ 2π=
A
4
4 4 2
2
B
.
4 2 答:蚂蚁爬行的最短路线为
1
C
已知圆锥底面半径为10cm，母线长为40cm. 求它的侧面展开图的圆心角和全面积
B
S
A
解:
(1) r 10cm
l 2r 20cm
B
na l , a 40cm 180 180 l 180 20 0 n 90 a 40 A 1 2 S全=S侧+S底 20 40 10 500 2
S
例2 圆锥形烟囱帽的母线长为80cm，高 38.7cm （1）求这个烟囱帽的面积。 （2）以1：40的比例画出这个烟囱帽的展 开图
解： （ 1 ） l 80cm.h 38.7cm
r l h 80 38.7 70(cm)
2 2 2 2

A
CF
图3-7
做一做
一个直六棱柱的上、下底面分别是边长为1cm 的正六边形，侧棱长为10cm.请计算它的表 面积.
初中数学课件
灿若寒星*****整理制作
浙教版九年级下
3.4简单几何体的表面展开图
几何体的展开图在生产时间中有着广泛的应用.通过 几何体的展开图可以确定和制作立体模型，也可以计算 相关集合体的侧面积和表面积.
观察与思考
某外包装盒的形状是棱柱（图3-1），它的两底面都是水平的 ，侧棱都是竖直的（这样的棱柱叫做直棱柱）.沿它的棱剪 开、铺平，就得到了它的平面展开图（图3-2）.
（1） （3）
（2） （4）
练习
下列各图是几何体的平面展开图，猜想下列展开图可折成什 么立体图形，并指出围成的几何体的形状.
一起探究
图3-4和图3-5分别是某几何体的三视图.（单位： mm）
（1）请分别说出他们所对应的几何体的名称. （2）分别计算这两个几何体的表面积. （3）小明认为，图3-5所示三视图所对应的几何体
关系？
做一做
1.制作圆锥并计算其相关的量. （1）在纸上画一个半径为6cm，圆心角为216°的扇形. （2）将这个扇形剪下来，按图37-36所示围成一个圆锥. （3）指出这个圆锥的母线长，并求圆锥的高和底面的半径（
粘合部分忽略不计）.
S
216°
A
OB
做一做
2.图3-3是四个几何体的平面展开图，请用纸分别复制下来，猜想下列展 开图可折成什么立体图形，实际动手折一下，并指出围成的几何体的 形状.
观察与思考
底面
侧棱 侧面
底面
图3-1
图侧面是什么形状的？ 2.这个棱柱的上、下底面的形状一样吗？他们各有几条边？ 3.侧面的个数与底面图形的边数有什么关系？ 4.这个棱柱有几条侧棱？它们的长度之间有什么关系？ 5.侧面展开图的长和宽分别与棱柱底面的周长和侧棱长有什么

• S侧=2πr • =2× π ×1 ×2.5 • =5 π （cm²） • S全=2πr²+ 2πrL • = 2πr×1²+ 2πr×1 ×2.5 • = 7 π （cm²） • 答：这个圆柱的侧面积为5 π cm²，全面积 为 7π cm².
①铝皮： S侧=ch =π×6×2.6 =π×15.6 =15.6π（dm²）
②羊皮： 2S底=πr²×2 =π×3²×2 =π×18 =18π（cm²）
• 3.如图，把一个圆柱形木块沿它的轴剖开 ，得矩形ABCD。已知AD＝18cm，AB＝ 30cm，求这个圆柱形木块的表面积（精 确到1cm2）
2cm
.
2cm
.
小组合作计算出圆柱的表面积:
①S侧=ch =π×2×2 =4π（cm²） ③S表= S侧＋ 2S底 ②S底=πr² =4π＋2×π =π×1² =4π＋2π =π（cm²） =6π（cm²）
判断：（对的画“√”，错的画“×”） 1、圆柱的侧面展开可以得到一个矩形，这个矩形的长等于 圆柱的底面直径，ห้องสมุดไป่ตู้等于圆柱的高。 （ ）
×
2、给大厅的圆柱刷油漆，刷油漆的部分面积是圆柱的侧 面积。
（√
）
3、圆柱形通风管的表面积等于它的侧面积。（
√
）
4、一个圆柱的侧面展开是正方形，它的底面周长和高 相等。 （ ）
√
• 例3.如图为一个圆柱的三视图.以相同的比 例画出它的表面展开图，并计算它的侧面 积和全面积. （结果保留π）
2.5
1
分析：由图知，圆柱底面 的半径r为1cm,母线长L为 2.5cm 。因此圆柱的表面 展开图中两个底面应画成 半径为1cm 的圆，侧面展 开图应画成2πr=2π×1=2π (cm)，宽为2.5cm的长方 形。

12 3456
一三二型
12 345
6
12 345
6
12 345 6
二个三型
126 345
例1
请分别用1，2，3，4，5，6中的同一个数字 表示立方体和它的展开图中各对对应的面.
2 5 1 34
6
56 45 61
32 13 24
让思维更活跃一点!
如图是一个正方体纸盒的展开图，图中的6个 正方形中分别已填入了-1、7、2 、a、b、c，使展 开图折叠成正方体后相对面上的两个数互为相反
• 17、儿童是中心，教育的措施便围绕他们而组织起来。2021/7/302021/7/302021/7/302021/7/30
• 2、Our destiny offers not only the cup of despair, but the chalice of opportunity. (Richard Nixon, American President )命运给予我们的不是失望之酒，而是机会之杯。二〇二一年六月十七日2021年6月17日星期四 • 3、Patience is bitter, but its fruit is sweet. (Jean Jacques Rousseau , French thinker)忍耐是痛苦的，但它的果实是甜蜜的。10:516.17.202110:516.17.202110:5110:51:196.17.202110:516.17.2021 • 4、All that you do, do with your might; things done by halves are never done right. ----R.H. Stoddard, American poet做一切事都应尽力而为，半途而废永远不行6.17.20216.17.202110:5110:5110:51:1910:51:19 • 5、You have to believe in yourself. That's the secret of success. ----Charles Chaplin人必须相信自己，这是成功的秘诀。-Thursday, June 17, 2021June 21Thursday, June 17, 20216/17/2021

【解题关键】将实际问题转换为数学模型.
根据题意,下部圆柱的底面积12m2，高h2为1.8m;
上部圆锥的高hl=3.2－1.8=1.4m;
l
圆柱底面圆半径r=
12
≈1.954

h1
(m)
S圆柱的侧面积=2πrh2=2π×1.954×1.8 ≈22.10(m2)
圆锥的母线l= ℎ12 + 2 ≈2.404 (m)
锥的全面积是________cm
400π 2.
【分析】S全=S底+S侧
=πr2+πrl=π×102+π×10×30=400π．
讲授新课
2、(1)圆锥的母线长为5，圆锥高为3，则该圆锥的侧面积为
________；
20π
(2)已知圆锥的底面半径为7cm，高为24cm，则该圆锥的侧面积为
175π 2.
________cm
个这样的锚标浮筒，需要用多少锌？
【详解】解：由图形可知圆锥的底面圆的半径为400mm=0.4m，
圆锥的高为300mm=0.3m，则圆锥的母线长为： 0. 32 + 0. 42 ＝0.5m．
∴圆锥的侧面积＝π×0.4×0.5＝0.2π（m2），
∵圆柱的高为800mm=0.8m．圆柱的侧面积＝2π×0.4×0.8＝0.64π（m2），
扇形，则这个圆锥的底面圆半径是________cm.
1
【分析】
圆锥底面圆的周长2πr=扇形的弧长l弧，
×
2πr= =
，解得：r=1．



或直接公式法：n=


·360，即120= ·360．

当堂检测
5、如图，沿一条母线将圆锥侧面剪开并展开，得到一个扇形，

的表面积，就是图3-5中的两个主视图、两个左视 图和一个府视图的面积的和.你认为小明的想法正 确吗？为什么？
一起探究
—— 40 —— —— 40 —— —— 40 —— —20—
—20—
—20—
主 视 图
俯 视 图
—20—
—20—
左 视 图
主 视 图
—20—
俯 视 图
—20—
左 视 图
—— 40 ——
经过点（-1，2）和（1，0），且与y轴相交于负半轴. (1)给出四个结论：①a＞0;②b＞0;③c＞0； ④a+b+c=0.其中正确结论的序号是__①___④___.
(2)给出四个结论:①abc＜0;②2a+b＞0;③a+c=1; ④a＞1.其中正确结论的序号是___②___③____.
课堂小结
1.一般地，我们可以用配方法将 yax2bxc配方成 yaxb24acb2. 2a 4a
(1)二次函数 yax2bxc ( a≠0)的图像是一条 __抛__物__线___；
(2)直线 x b 2a
是二次函数
yax2bxc的对称轴；顶点坐
标是(
b
4acb2 ,
).
2a 4a
2.二次函数y=ax2+bx+c(a≠0)的图像和性质
观察与思考
底面
侧棱 侧面
底面
图3-1
图3-2
观察与思考
1.这个棱柱有几个侧面？每个侧面是什么形状的？ 2.这个棱柱的上、下底面的形状一样吗？他们各有几条边？ 3.侧面的个数与底面图形的边数有什么关系？ 4.这个棱柱有几条侧棱？它们的长度之间有什么关系？ 5.侧面展开图的长和宽分别与棱柱底面的周长和侧棱长有什么

(2) 直棱柱的侧面积与底面周长及侧棱长有怎样的关系？
直棱柱的侧面积=底面周长× 侧棱长
随堂演练 1．下列各图中，经过折叠能围成一个立方体的是 ( A )
2．如图是一个长方体的包装盒，它的平面展开图是 ( A )
3．把如图中的三棱柱展开，所得到的展开图是 ( B )
4．如图是正方体的一种展开图，其中每个面上都标有 一个数字．那么在原正方体中，与数字“2”相对的面上 的数字是 ( B )
例题讲授 例1 图1 是一个立方体的表面展开图吗？如果是，分别用1，2，3， 4，5，6中的同一个数字表示立方体和它的展开图中各对对应的面 （只要求给出一种表示法）. 分析 可以先用折叠的方法试一试，看
它能否折成一个立方体.
解： 图1是一个立方体的表面展开图，各对应面上的数字表示如图2和图3.
2 4
A．1 B．4 C．5 D．6
5．右图是一个正方体纸盒的表面展开图，去掉其中一 个正方形，可以折成一个无盖的正方体盒子，去掉的 这个正方形的编号是__答__案__不__唯__一___，__如__1．(只填1个)
7.某工厂要加工一批正六棱柱形状的食品盒，其三视图如图， （单位：cm）问制作一个食品盒至少需要的硬纸板的面积为多少？
36 10
36 10
解：上下底面面积 3 102 6 2
4 300 3(cm2 )
答：所需面积为
六个侧面面积
36 10 6
2160(cm2 )
所需硬纸板面积为
300 3 2160(cm2 )
直棱柱的表面展开图
直棱柱的表 面展开图
立方体的各种表面展开图
用直棱柱表面展开图 进行相关计算
a b
h
h
b
甲

•
29、在一切能够接受法律支配的人类 的状态 中，哪 里没有 法律， 那里就 没有自 由。— —洛克
•
30、风俗可以造就法律，也可以废除 法律。 ——塞·约翰逊
16、业余生活要有意义，不要越轨。——华盛顿 17、一个人即使已登上顶峰，也仍要自强不息。——罗素·贝克 18、最大的挑战和突破在于用人，而用人最大的突破在于信任人。——马云 19、自己活着，就是为了使别人过得更美好。——雷锋 20、要掌握书，莫被书掌握；要为生而读，莫为读而生。——布尔沃
浙教版初中九年级下册数学：简单几
•
何体的表面展开图_课件1 26、我们像鹰一样，生来就是自由的，但是为了生存，我们不得不为自己编织一个笼子，然后把自己关在里面。——博莱索
•
27、法律如果不讲道理，即使延续时 间再长 ，也还 是没有 制约力 的。— —爱·科 克
•ቤተ መጻሕፍቲ ባይዱ
28、好法律是由坏风俗创造出来的。 ——马 克罗维 乌斯
END

第3章 三视图与表面展开图
3.4 简单几何体的表面展开图
第2课时 圆柱体的表面展开图
浙教版·九年级下册
1．(4分)(2017·湖州)如图是按1∶10的比例画出的一个几何体的三视图，则该几何体的侧面积是 (D) A．200 cm2 B．600 cm2 C．100π cm2 D．200π cm2
2．(4分)如图是一个工件的三视图，图中标有尺寸，则这个工件的体积是( B ) A．13π cm3 B．17π cm3 C．66π cm3 D．68π cm3
6．(4分)已知矩形ABCD的一边AB＝2 cm，另一边AD＝4 cm，则以直线AD为轴旋转一周所得到的图形是 _圆__柱_，其侧面积是_1_6_π_cm2.
8．(10分)如图是一个立体图形的三视图，请根据视图写出该立体图形的名称，并计算该立体图形的 体积．(结果保留π)
9.(12分)如图，有一圆柱体高为8π cm，底面圆的半径为6 cm，AA1，BB1为相对的两条母线，在点A 处有一只蜘蛛，点B1处有一只苍蝇，蜘蛛沿圆柱体侧面爬到B1处吃掉苍蝇，问蜘蛛所爬过的最短路径 长是多少？
解：蜘蛛所爬过的最短路径长为 （8π）2＋（6π）2＝10π(cm)．
10. (6分)如图，矩形ABCD中，AB＝a，BC＝b，a＞b，以AB边为轴将矩形绕其旋转一周形成圆柱体甲， 再以BC边为轴将矩形绕其旋转一周形成圆柱体乙，记两个圆柱体的体积分别为V甲，V乙，侧面积分别 为S甲，S乙，则下列式子正确的是( B ) A．V甲＞V乙，S甲＝S乙 B．V甲＜V乙，S甲＝S乙 C．V甲＝V乙，S甲＝S乙 D．V甲＞V乙，S甲＜S乙
13. (12分)从卫生纸的包装纸上得到以下资料：两层300格，每格11.4 cm×11 cm，如图①.用尺量出 整卷卫生纸的半径(R)与纸筒内芯的半径(r)，分别为5.8 cm和2.3 cm，如图②.那么该两层卫生纸的 厚度为多少厘米？(π取3.14，结果精确到0.001 cm)

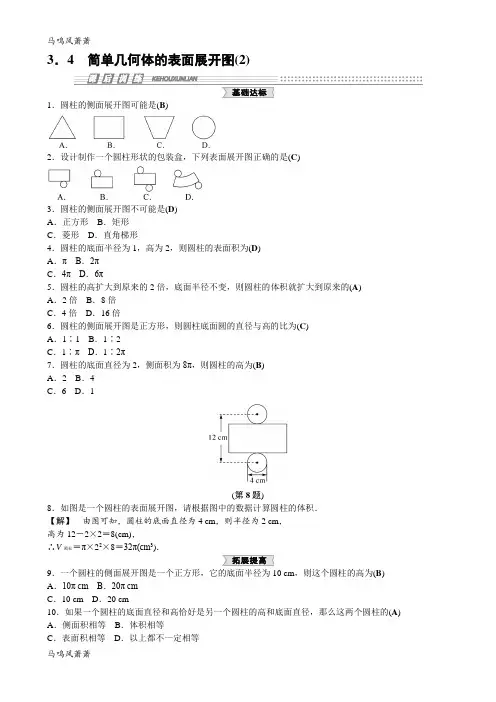
3．4简单几何体的表面展开图(2)1．圆柱的侧面展开图可能是(B)2．设计制作一个圆柱形状的包装盒，下列表面展开图正确的是(C)3．圆柱的侧面展开图不可能是(D)A．正方形B．矩形C．菱形D．直角梯形4．圆柱的底面半径为1，高为2，则圆柱的表面积为(D)A．π B．2πC．4π D．6π5．圆柱的高扩大到原来的2倍，底面半径不变，则圆柱的体积就扩大到原来的(A)A．2倍B．8倍C．4倍D．16倍6．圆柱的侧面展开图是正方形，则圆柱底面圆的直径与高的比为(C)A．1∶1 B．1∶2C．1∶π D．1∶2π7．圆柱的底面直径为2，侧面积为8π，则圆柱的高为(B)A．2 B．4C．6 D．1(第8题)8．如图是一个圆柱的表面展开图，请根据图中的数据计算圆柱的体积．【解】由图可知，圆柱的底面直径为4 cm，则半径为2 cm，高为12－2×2＝8(cm)，∴V圆柱＝π×22×8＝32π(cm3)．9．一个圆柱的侧面展开图是一个正方形，它的底面半径为10 cm，则这个圆柱的高为(B) A．10π cm B．20π cmC．10 cm D．20 cm10．如果一个圆柱的底面直径和高恰好是另一个圆柱的高和底面直径，那么这两个圆柱的(A) A．侧面积相等B．体积相等C．表面积相等D．以上都不一定相等11．有一张矩形纸片如图所示，剪成两个圆和一个矩形，正好可以做成一个圆柱，求这个圆柱的体积．(第11题)【解】 ∵圆柱的高为20 cm ，底面直径为20 cm ，∴底面半径为10 cm ，∴V 圆柱＝π×102×20＝2000π(cm 3)．12．请阅读下列材料：问题：如图①，圆柱的底面半径为1，BC 是上底面的直径，圆柱高AB 为5，求一只蚂蚁从点A 出发沿圆柱表面爬行到点C 的最短路线．小明设计了两条路线：路线1：高线AB ＋底面直径BC ，如图①所示．路线2：侧面展开图中的线段AC ，如图②所示．(第12题)(1)设路线1的长度为l 1，则l 21＝__49__；设路线2的长度为l 2，则l 22＝25＋π2，所以选择路线__2__(填“1”或“2”)较短；(2)小明把条件改成：“圆柱的底面半径为5 dm ，高AB 为1 dm ”继续按前面的路线进行计算．此时，路线1：l 21＝121；路线2：l 22＝1＋25π2，所以选择路线__1__(填“1”或“2”)较短；(3)请你帮小明继续研究：当圆柱的底面半径为2 dm ，高为h (dm)时，应如何选择上面的两条路线才能使蚂蚁从点A 出发沿圆柱表面爬行到点C 的路线最短．【解】 (3)当圆柱的底面半径为2 dm ，高为h (dm)时，l 21＝(AB ＋BC )2＝(h ＋4)2，l 22＝AC 2＝AB 2＋lBC ︵2＝h 2＋4π2，∴l 21－l 22＝(h ＋4)2－h 2－4π2＝－4π2＋8h ＋16＝－4[(π2－4)－2h ]．当(π2－4)－2h ＝0，即h ＝π2－42时，l 21＝l 22，即l 1＝l 2，选择路线1或路线2都可以； 当h ＞π2－42时，l 21＞l 22，即l 1＞l 2，应选择路线2； 当h ＜π2－42时，l 21＜l 22，即l 1＜l 2，应选择路线1.初中数学试卷鼎尚图文**整理制作。

解：若选图甲，可得表面展开图及尺寸标注如下图. a
b
甲
b b ab a
（3）利用你所选的一种纸样，求出包 装盒的侧面积和表面积（侧面积与两 个底面积的和） .
解:由右图可得,包装盒的侧面积为
S侧= （b a b a)h
2ah 2bh;
S表=S侧+2S底
2ah 2bh 2ab
a b
h
A
B
---- “蜘蛛和苍蝇”问题
在一个长、宽、高 分别为3米，2米，2米的长方体房间 内，一蜘蛛在一面的中间,离天花板0.1米处(A点)，苍蝇 在对面墙的中间,离地面0.1米处(B点),试问:蜘蛛去捉苍蝇 需要爬行的最短距离是多少?
A
B
将立方体沿某些棱剪开后铺平,且六个面连在一起， 这样的图形叫立方体的表面展开图。
P
l h
A
Or B
圆锥的侧面积和全面积
如图:设圆锥的母线长为a,底面半径为r.则 圆锥的侧面积公式为：
S侧
1 2
2r
l
rl
A
P
l 2r
hl OrB
全面积公式为：
S全 S侧 S底
= πrl ＋πr2
例1、根据圆锥的下列条件，求它的侧面积和全面积
（1） r=12cm, l=20cm
（2） h=12cm， r=5cm
4
4
5632 5 6 3 2
1 (1)
1 (2)
4 5632 (3) 1
6
4 56 32
(4) 1
4 5632
1 (5)
4 5 6 32 (6) 1
4 563 (7) 1 2
4 56
(8)
3 12
56 (9)

∴∠BAD = 60°.在RtΔABC中， ∠BAD = 60°, AB = 3.
∴ BD = 3 3 2
答： 解：
它 将 爬圆 行的锥 最短沿 路线A 是B 23 展 3. 开成扇形ABB，
垂足为D.
则点C是BB的中点，
过点B作BD
AC，
BAB r 360 120 l
BAD 60.在RtABC中， BAD 60, AB 3.
5.圣诞节将近, 某家商店正在制作圣诞节的 圆锥形纸帽。已知纸帽的底面周长58cm，高为 20cm，要制作20顶这样的纸帽至少要用多少 平方厘米的纸？（结果精确到0.1cm2）
解：设纸帽的底面半径为rcm，母线长为lcm，
r 58
2
l ( 58 )2 202 22.03(cm)
360
2
如图,圆锥的底面半径为1,母线长为4,一只 蚂蚁要从底面圆周上一点B出发,沿圆锥侧面爬 行一圈再回到点B,问它爬行的最短路线是多少?
A
B
C
解:设圆锥的侧面展开图为扇形ABB’, ∠BAB’=n°
连接BB’,即为蚂蚁爬行的最短路线
∵ 圆锥底面半径为1,母线长为4
∴
2π=
4nπ 180
B’
n=90
例1 如图3-48为一个圆柱的三视图.以相同的比例画出 它的表面展 开图，并计算它的侧面积和全面积(果 保留π).
分析：由图3-48知，圆柱底面圆的半
径r为0.9cm，母线长l 为
2.4 cm. 因此圆柱的表面展 开图中两个底面应画成半 径为0.9cm的圆，侧面展开
图应画成长为2πr=2π×0.9
， l
∴∠BAD = 60°.在RtΔABC中
∠BAD = 60° , AB = 3.

【例 2】 如图 3-4-10，在矩形 ABCD 中，AB＝2 cm，AD＝6 cm， 求分别以 AB，AD 所在的直线为轴旋转后所得圆柱的侧面积．
图 3-4-10 【解析】 设以 AB 所在的直线为轴旋转后所得圆柱的侧面积为 S1， 以 AD 所在的直线为轴旋转后所得圆柱的侧面积为 S2，则有： S1＝2π·AD·AB＝2π×6×2＝24π(cm2)， S2＝2π·AB·AD＝2π×2×6＝24π(cm2)． 【答案】 24π cm2如解图，连结 OA，OD，过点 O 作 OE⊥AD，垂足为 E.易得∠AOD ＝360°×1－23＝120°.
(例 3 解) ∵OE⊥AD，∴∠AOE＝12×120°＝60°，AE＝12AD＝12 cm， ∴AO＝siAn6E0°＝12÷ 23＝8 3(cm)，即⊙O 的半径为 8 3 cm. (2)设圆柱的表面积为 S，则 S＝2S 圆＋S 侧， 2S 圆＝2π×(8 3)2＝384π(cm2)， S 侧＝2π×8 3×25＝400 3π(cm2)， ∴S＝(384＋400 3)π cm2. 【答案】 (1)8 3 cm (2)(384＋400 3)π cm2
学习指要
知识要点
1．圆柱的有关概念： 圆柱可以看做由一个矩形绕它的一条边(BC)旋转一周，其余 各边所成的面围成的几何体(如图 3-4-8)．AB，CD 旋转所成 的面就是圆柱的两个底面，是两个半径相同的圆．AD 旋转所 成的面就是圆柱的侧面，AD 不论转动到哪个位置，都是圆柱 的母线． 2．如果沿圆柱的任意一条母线把圆柱的侧面“剪开”，铺平，那么就得到圆柱的 侧面展开图，这个侧面展开图是一个矩形．这个矩形的一条边等于圆柱的母线长， 也就等于圆柱的高，另一条与它相邻的边等于底面圆的周长． 3．圆柱的侧面积和全面积公式： 圆柱的侧面积：S 侧＝l·2πr＝2πrl； 圆柱的全面积：S 全＝2πrl＋2πr2＝2πr(r＋l)． 其中 r 为圆柱的底面半径，l 为圆柱的母线．