第12章 聚类分析

第一章练习题一、名词解释人员素质测评；素质(广义）二、填空题(可出选择题）1．素质包括以下三大类: 、、；2．心理素质包括: 与；3．人员素质测评的方法包括: 、、、；4．人员素质测评的主体包括：、 ;5．心理测量测查的对象具有、、等特点；6．人员素质测评的对象是及；7．人才测评的三个功能是、、；8．人才测评的作用包括对和对所起的作用；9．人才测评对组织所起的作用包括、、；10．人才测评对个人所起的作用包括、、。

三、简答题1．阐述评价（评定）与测量的联系与区别？2．简述人员素质测评的特点？3．简述人员素质测评与人才素质测评的联系与区别？第二章练习题一、名词解释察举;九品中正制；科举制二、填空题1．中国古代人才选拔制度包括：、、；2．察举制度用来测评人才的方法有许多，仅两汉就有常科：、、、四行，后来规定岁举的科目以、为主；3．九品中正制，又称，是的一种选拔人才的举官制度；4．九品中正制中选拔人才的标准有三：、、；5．科举制是以后历代封建王朝常常采用的通过考试选拔官吏的一种制度;6．科举制度考试有、、三级;7．唐代科举从种类上讲只有和两种；8．三国时魏人所著的《人物志》对人才测评作了较为系统完整的论述;9．春秋时期，就对人的“才能”的观点加以了论述；10．战国时期，提出了“察能予官”，“以德就列”的原则；11．战国时期的把“德才”标准具体化为忠诚、谨慎、才能、智力、信用、廉洁、节守、仪态、行为等指标;12．古代人才测评用、、、以判断人才；13．我国古代使用的测评技术有、、；14．纸笔测验的典型形式有、、、；15．《吕氏春秋》提出了对内用“”,对外用“”的方法识别人才；16．实践鉴别法的核心是根据“”来作为选拔衡量使用人才的标准；17．文官考绩因素包括10项：、、、、、、、、、；18．文官接受培训的形式有、、、、、等；19．西方现代人才测评思想与技术发端于，开始于,最初源于教育实践中的需要；20．19世纪80年代至20世纪前10年，西方心理测验逐渐兴起，最有名的是测量智商的，这一量表是世界上第一个标准化的心理测验，由法国心理学家和医生于年提出，被称为是心理测验的鼻祖；21．美国最著名的比奈西蒙量表修订本是斯坦福大学教授在年指导修订的，即著名的量表；22．美国学者斯特朗于1927年编制出版的世界上第一个职业兴趣测验“”；23．“评价中心”技术综合运用了、和,使测评效果比原来更加可靠和有效；三、简答题1．试述察举制、九品中正制和科举制的特点？2．试述古代人才测评机制的缺点?第三章练习题一、名词解释职业;地位；角色；工作角色；二、填空题1．个人素质差异表现为两个方面，一是个性差异，如、和及其组合；二是个体的差异，如、、、、及等；2．以人员配置所凭借的方法为标准，大致可将人员配置原型划分为和；3．人员配置的经验原型的主要特征是和；4．以经验原型为指导进行人员配置，一般采用两种方法：一是，二是；5．在经验原型中, 、是人员配置的核心；6．人员配置的测评原型最显著的两大特征是和；7．美国约翰·霍普金斯大学心理学教授约翰·霍莱特认为人的个性素质基本类型有六种：、、、、、；8．人员素质测评的必要条件是、与的客观存在,充分条件是对个体素质与的探索；9．、、三大主指标及其数十个子指标,是当前比较流行的人员素质测评指标体系；10．职业能力测试子指标包括、、；11．职业人格子指标包括、、、；12．职业兴趣子指标包括、、、；13．人员素质测评应向与的方向发展,应把人员素质测评作为一种重要手段贯穿于整个的组织管理过程之中；14．借助，可以充分发挥素质测评在人力资源开发与管理中的优化作用；15．行为管理科学启示我们，通过素质测评对个体差异的揭示，按；按;16．著名的心理学家马斯洛理论把需求分成、、、、五类;17．提高人员素质测评效用的六大原则：、、、、、；18．人员素质测评的八个主要原则是: 、、、、、、、；19．人员素质测评的主要理论依据有、、等学科的知识;20．个性心理品质中的能力特征的两个方面是指和;21．人员素质测评所使用的各类人员的素质量表，是由、、、、五个方面的素质组成的一个复杂的系统，它包括分系统、分系统、分系统、分系统、分系统等;22．模糊数学被广泛应用于、、、等具有模糊现象的学科中；23．1965年美国控制论专家、加利福尼亚大学教授，对大量不确切现象进行了认真的分析，提出了原理;24．查德的模糊集合论原理用二句话概括就是、；25．查德借助经典数学这一工具，创立了用来定量表示模糊概念的模糊数学；26．当刺激情景是以文字或图形设计呈现时，测评即是形式；当刺激情景是经过精心设计，且以面对面的问答或谈话形式出现时，测评则是形式；当各种刺激情景是以自然的实际情形出现时，测评则是形式；三、简答题2．简述人员配置的经验原型的弊端?3．简述人员配置的测评原型与经验原型相比的优势表现在哪几个方面？6．简述素质测评待解决的几个问题?10．为了控制施测者主观性的消极影响,一般采取哪些方法？第四章练习题一、名词解释职业适应性测评的定义、内容；职业能力测评的定义、内容、领导人才测评的定义、内容、管理人才测评的定义、内容、科技人才测评的定义、内容.二、填空题10．选拔性测评是一种以为目的的测评，具有、、特点等；11．配置性测评以为目的，具有、、、等特点;12．人力资源最佳发挥状态的前提是、、、、；13．开发性测评也可以称为,以为目的，具有、、等特点;14．考核性测评又称，以为目的,具有、、、等特点;15．诊断性测评以为目的，具有、等特点；16．企业的人才测评针对不同的对象和目的，包括、、、、五种人员素质测评类型;17．职业适应性测评包括、、；18．生活特性测评包括、、、四个方面的测评;19．需求测评的五个维度是、、、、;20．需求测评一般采取的方式，其编制的量表包括5个方面，答案从到共7个分值；21．需求测评一般适用于、,一般不适用于。

分类分析 第 12 章质差异较大的观测分在不同的类，这称之为Q型聚类。

当聚类把变量（variables）作为分类对象时，称之为R型聚类。

这种聚类用在变量数目比较多，且相关性比较强的情形，目的是将性质相近的变量聚为同一个类，并从中找出代表变量，从而减少变量个数以达到降维的效果。

2．聚类分析的应用在科学研究和社会生产的许多领域（例如模式识别、机器学习、数据挖掘、图像处理和市场分析等）都渗透着聚类分析的研究和应用。

聚类分析的典型应用包括：在商业方面，帮助市场研究人员发现拥有不同特征的顾客组群，并可利用购买模式对其进行描述；在生物方面，可用来获取动物或植物群体内存在的层次结构（taxonomies），还能根据基因功能对其进行分类，由此获得对群体固有结构更深入的了解；它还可以利用地球观测数据库，帮助用户识别具有相似土地使用情况的区域；帮助研究者分类和识别互联网上的文档，以便发现潜在的信息；作为数据挖掘的一项功能，聚类分析还可以作为一个单独使用的工具，用来帮助分析数据的分布、了解数据的特征，找出感兴趣的数据子集作进一步分析；此外，聚类分析也可以作为其他算法的预处理步骤。

作为统计学的一个分支，聚类分析已有多年的研究历史，这些研究主要集中在基于距离的聚类分析方面。

现在的大多统计分析软件（例如S-Plus、SPSS和SAS等）都包含基于k-均值、k-中心等的聚类分析工具。

12.1.2 聚类分析的一般原理本节以最基础的对观测记录的Q型系统聚类法为例，简单介绍聚类的一般原理和步骤。

系统聚类是一种逐次合并类的方法，在规定了样品之间的距离和类与类之间的距离后，先让n个样品各自成为一类；开始时，因每个样品自成一类，类与类之间的距离与样品之间的距离是相等的；然后，将距离最近的两个类合并；如此重复，每次循环减少一个类别，直至所有的样品归为一类为止。

然而合并成一个类别就失去了聚类的意义，所以聚类过程应该在达到某个类水平数（即未合并的类数）时停下来，在此得到的聚类就是分析的结果。

第五、六、七章：抽样推断1.总体分布、样本分布、抽样分布总体分布：总体中各个数据的分布样本分布：样本中各个数据的分布抽样分布：样本统计量的概率分布总体的分布通过直方图观察，但一般不可能得到所有的数据，也就不能直接观察到总体分布。

只要知道总体的分布类型和反映总体分布特征的参数就能够满足需要。

样本分布也称为经验分布，样本来源于总体，会包含总体的信息和特征，特别当样本容量较大时，样本的分布会很接近总体分布，但样本是随机抽取的，一般与总体分布有一定差异。

抽样分布是说明样本分布特征的统计量的分布，对它的理解是建立在反复抽样的基础上，样本是随机抽取的，不同的样本会有不同的统计量值，一个总体可以有很多个不同的样本，这样一个统计量就会有很多不同的取值，这些不同值的分布就是抽样分布。

由于在实践中对于同一总体我们不会反复抽取很多样本，因此，抽样分布一般不能直接观察到，仅是一种理论分布。

抽样分布揭示了样本统计量与总体参数的内在联系，为统计推断提供了理论基础。

2.总体单位与抽样单位、样本容量与样本可能数目3.统计量、总体参数及统计量的标准化统计量是样本数据的函数，在实际抽样之前，由于是样本随机的，统计量也是随机的，但在抽取样本之后，样本已经确定，统计量也就是确定的，不包含任何未知变量。

总体参数是说明统计总体的数据特征值，一般是确定但未知的，是待估计的。

统计量的标准化是统计推断的必要过程，是将具体的统计量转化为已知分布的统计量，转化以后就可以确定一定区间的概率。

4.统计误差、抽样误差、抽样标准误差与抽样边际误差统计误差是统计调查得到的值与客观实际值之间的差异。

包括抽样误差和非抽样误差。

非抽样误差又称工作误差或调查误差，是指调查登记过程中由于登记、过录、计算等原因引起的误差。

在全面调查和非全面调查中都有可能存在。

抽样误差也称为随机误差，是指在坚持了随机抽样的情况下，由于样本的随机性造成样本统计量与总体参数的差异。

样本是随机的，样本的统计量也是随机的，而总体参数是唯一的，因而抽样误差也是随机的。

第十二章因子分析（大学虎统计）1， 引出因子分析的定义：作个比喻，对面来了一群女生，我们一眼就能够分辨出孰美孰丑，这是判别分析；并且我们的脑海中会迅速的将这群女生分为两类；美的一类，丑的一类，这是聚类分析。

我们之所以认为某个女孩漂亮，是因为她具有漂亮女孩所具有的一些共同点，比如漂亮的脸蛋，高挑的身材，白皙的皮肤，等等。

其实这种从研究对象中寻找公共因子的方法就是因子分析（Factor Analysis ）。

因子分析也是利用降维的思想，把每一个原始变量分解成两部分，一部分是少数几个公共因子的线性组合，另一部分是该变量所独有的特殊因子，其中公共因子和特殊因子都是不可观测的隐变量，我们需要对公共因子作出具有实际意义的合理解释。

因子分析的思想源于1904年查尔斯，斯皮曼（charles spearman ）对学生考试成绩的研究，目前因子分析已经在很多领域得到广泛应用。

本章主要容包括：因子分析的理论简介，因子分析的matlab 实现，因子分析具体案例。

12.1因子分析简介 12.11 基本因子分析模型设P 维总体'(,,...,)p x x x x =的均值为'12(,,...,)p μμμμ=协方差矩阵为()ij p pσ⨯=∑，相关系数矩阵为()ij p pR ρ⨯=。

因子分析的一般模型为111111221122211222221122.........m m m m p p p p pm m p x a f a f a f x a f a f a f x a f a f a f μεμεμε=+++++⎧⎪=+++++⎪⎨⎪⎪=+++++⎩（12.1）其中，12,,...,mf f f 为m 个公共因子，i ε是变量(1,2,...)i x i p =所独有的特殊因子他们都是不可观测的隐变量。

称(1,2,...;1,2,...,)ij a i p j m ==为变量ix 在公共公共因子jf 上的截荷，它反映了公共因子对变量的重要程度，对解释公共因子具有重要的作用。

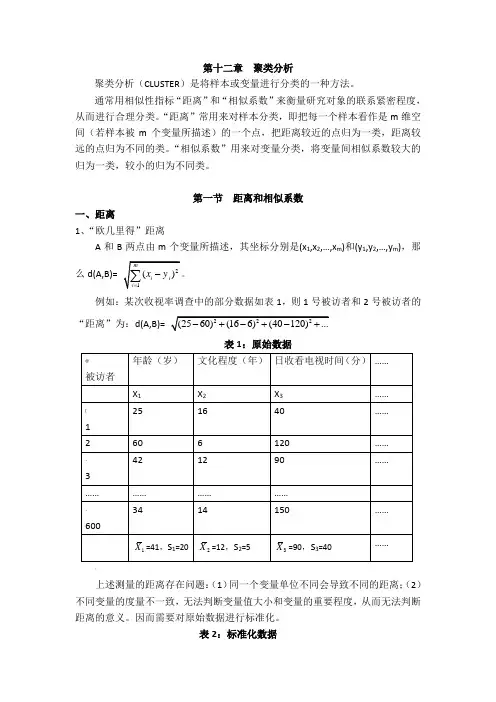
第十二章聚类分析聚类分析（CLUSTER）是将样本或变量进行分类的一种方法。

通常用相似性指标“距离”和“相似系数”来衡量研究对象的联系紧密程度，从而进行合理分类。

“距离”常用来对样本分类，即把每一个样本看作是m维空间（若样本被m个变量所描述）的一个点，把距离较近的点归为一类，距离较远的点归为不同的类。

“相似系数”用来对变量分类，将变量间相似系数较大的归为一类，较小的归为不同类。

第一节距离和相似系数一、距离1、“欧几里得”距离A和B两点由m个变量所描述，其坐标分别是(x1,x2,…,x m)和(y1,y2,…,y m)，那么d(A,B)=例如：某次收视率调查中的部分数据如表1，则1号被访者和2号被访者的Array“距离”为：d(A,B)=表1：原始数据-上述测量的距离存在问题：（1）同一个变量单位不同会导致不同的距离；（2）不同变量的度量不一致，无法判断变量值大小和变量的重要程度，从而无法判断距离的意义。

因而需要对原始数据进行标准化。

表2：标准化数据2、SPSS 聚类分析中提供的距离（1）欧式距离（EUCLID ），等于 （2）欧式距离的平方（SEUCLID ），等于变量差2+变量差2+……（3）曼哈顿距离（BLOCK ），等于变量差的绝对值之和（4）切比雪夫距离（CHEBYCHEV ），等于变量差中绝对值最大者（5）幂距离POWER(p,r)，等于变量差的绝对值的p 次方之和，再求r 方根。

2、相似系数（1）变量间的相关系数即皮尔逊相关系数； …（2）变量间的夹角余弦，即将两变量分别看成n 维空间的向量时的夹角余弦值。

相关系数一般针对定距变量，对于定类变量特别是二项变量也可引入虚拟变量后计算相关系数。

例1：假定5个样本（人）具有如下指标：（1）请对个体进行分类；（2）对变量进行分类。

表3：五个人的六种身体特征指标解：变量中包含定距和定类变量，可以全部变成虚拟变量（也可将后四个虚拟），令X 1= ；X 2= ；X 3= ； ; X 4= ；X 5= ；X 6= ，表3可转化为表4：（1）根据两个个体共同特征的多少来对个体分类，以欧式距离的平方来进行聚类，个体之间的距离越小越相似，可求得： d 2(1,2)=(0-1)2+(0-1)2+(0-1)2+(1-0)2+(0-0)2+(1-0)2=5； d 2(1,3)=(0-0)2+(0-1)2+(0-0)2+(1-1)2+(0-0)2+(1-0)2=2； d 2(1,4)=(0-0)2+(0-0)2+(0-1)2+(1-0)2+(0-0)2+(1-1)2=2；d 2(1,5)=(0-1)2+(0-1)2+(0-1)2+(1-0)2+(0-1)2+(1-0)2=6；同理计算其他距离，得到下表：表5：5个体间距离1,身高≥170 0,身高＜170 1,体重≥130 ^1,双眼皮 0,单眼皮1,高鼻梁 0,低鼻梁1,用左手 0,用右手1,女 0,男根据距离大小，判断相似程度。

市场研究——聚类分析法
聚类分析法在市场研究中有着广泛的应用。

通过对市场中消费者、产品、品牌等进行聚类分析，可以帮助市场研究人员更好地理解市场细分和
目标受众，并制定针对不同群体的市场营销策略。

下面将详细介绍聚类分
析法的原理、应用和步骤。

聚类分析的原理是将数据样本划分为不同的类别或群组，使得同类之
间的差异最小，而不同类之间的差异最大。

输入聚类分析的数据通常是多
维的，每个维度代表一个变量。

聚类分析的目标是找到一个最优的聚类方案，使得相同类别内的样本相似度最高，而不同类别的样本相似度最低。

聚类分析法的应用非常广泛。

在市场研究中，它可以用于客户细分、
产品定位、市场定位等方面。

通过对消费者进行聚类，可以发现隐藏在市
场中的不同消费者群体，并确定他们的特征、需求和偏好。

对产品和品牌
进行聚类分析，则可以帮助确定产品和品牌的差异化定位和市场竞争策略。

需要注意的是，聚类分析法只是一种分析工具，通过聚类分析得到的
结果并不一定代表真实的市场现象，仅供市场研究人员参考和决策。

在市场研究中，聚类分析法的应用是非常重要的。

它能够帮助市场研
究人员更好地理解市场细分和目标受众，并制定针对不同群体的市场营销
策略。

随着数据量的不断增加和分析技术的不断发展，聚类分析法在市场
研究中的应用前景将更加广阔。

聚类分析方法聚类分析是一种常用的数据分析方法，它可以帮助我们将数据集中的对象按照它们的相似性进行分组。

通过聚类分析，我们可以发现数据中的内在结构和规律，从而更好地理解数据。

在本文中，我们将介绍聚类分析的基本概念、常见的聚类方法以及聚类分析的应用场景。

首先，让我们来了解一下聚类分析的基本概念。

聚类分析是一种无监督学习方法，它不需要预先标记的训练数据，而是根据数据对象之间的相似性来进行分组。

在聚类分析中，我们通常会使用距离或相似度作为衡量对象之间关系的指标。

常见的距离指标包括欧氏距离、曼哈顿距离和余弦相似度等。

通过计算对象之间的距离或相似度，我们可以将它们划分到不同的类别中，从而实现数据的聚类。

接下来，让我们来介绍一些常见的聚类方法。

最常用的聚类方法包括层次聚类、K均值聚类和密度聚类。

层次聚类是一种基于对象之间相似性构建层次结构的方法，它可以分为凝聚式层次聚类和分裂式层次聚类。

K均值聚类是一种迭代的聚类方法，它将数据对象划分为K个类别，并通过迭代优化来找到最优的聚类中心。

密度聚类是一种基于数据密度的聚类方法，它可以发现任意形状的聚类簇，并对噪声数据具有较强的鲁棒性。

最后，让我们来看一些聚类分析的应用场景。

聚类分析可以应用于各个领域，例如市场营销、生物信息学、社交网络分析等。

在市场营销中，我们可以利用聚类分析来识别不同的消费群体，并针对不同群体制定个性化的营销策略。

在生物信息学中，聚类分析可以帮助我们发现基因表达数据中的基因模式，并识别相关的生物过程。

在社交网络分析中，我们可以利用聚类分析来发现社交网络中的社区结构，并识别影响力较大的节点。

总之，聚类分析是一种非常有用的数据分析方法，它可以帮助我们发现数据中的内在结构和规律。

通过本文的介绍，相信大家对聚类分析有了更深入的了解，希望能够在实际应用中发挥其价值，为各行各业的发展提供有力支持。

聚类分析原理聚类分析是一种常用的数据分析方法，它可以将数据集中的个体按照相似性进行分组，从而揭示数据内在的结构和规律。

在实际应用中，聚类分析被广泛应用于市场细分、社交网络分析、生物信息学、图像处理等领域。

本文将介绍聚类分析的原理及其常见的方法。

首先，聚类分析的原理是基于样本之间的相似性进行分组。

相似的样本被归为同一类别，而不相似的样本则被划分到不同的类别中。

在进行聚类分析时，我们需要选择合适的相似性度量方法，常见的相似性度量包括欧氏距离、曼哈顿距离、余弦相似度等。

通过计算样本之间的相似性，我们可以构建出样本之间的相似性矩阵，从而为后续的聚类分析提供依据。

其次，聚类分析的方法包括层次聚类和非层次聚类两种。

层次聚类是一种自下而上或自上而下的聚类方法，它通过计算样本之间的相似性来构建聚类树，从而实现对样本的分层聚类。

非层次聚类则是一种直接将样本划分为不同类别的方法，常见的非层次聚类方法包括K均值聚类、DBSCAN聚类等。

不同的聚类方法适用于不同的数据特点和分析目的，选择合适的聚类方法对于获得准确的聚类结果至关重要。

此外，聚类分析还需要考虑到聚类数目的确定。

在进行聚类分析时，我们需要事先确定聚类的数目，这也是聚类分析的一个重要参数。

常见的确定聚类数目的方法包括肘部法则、轮廓系数法等。

通过选择合适的聚类数目，我们可以获得更加准确和有意义的聚类结果。

总之，聚类分析是一种重要的数据分析方法，它可以帮助我们揭示数据内在的结构和规律。

在进行聚类分析时，我们需要选择合适的相似性度量方法、聚类方法和确定聚类数目的方法，以获得准确和有意义的聚类结果。

希望本文能够帮助读者更好地理解聚类分析的原理和方法，从而更好地应用聚类分析于实际问题中。

第12章群落参数统计分析群落生态学家在解释和测度动植物群落特征特性时面对的是一类特殊的统计问题。

有些群落研究，例如能量分析，只需要使用一般的统计学方法、原理，就可以对群落内物种的丰富度进行估计。

但是，有些群落研究，需要使用一些新的参数，在群落水平来度量各个群落之间的相似性(similarity)。

DPS系统提供了常用的群落相似性参数估计，包括二项分布系数和距离系数。

前者可根据定性或定量调查资料通过计算各个生物群落间的相似系数和不相似(距离)系数来描述各个样本间的相似性测度；后者则根据定量资料，对群落的相似性进行测度。

植物生态学家为分析群落格局与环境关系，使用了大量的多变量统计分析技术。

如聚类分析、非线性映射分析、对应分析、主成分分析、因子分析及典型相关分析等。

这些分析技术将在后面章节中介绍。

本章仅介绍极点排序分析技术和对排序效果进行检验的方法。

群落物种多样性(diversity)是群落最直观的特征。

目前描述群落特征，比较群落之间差异时，一般都是使用多样性指数。

因此多样性指数在当今群落生态学中的应用十分广泛。

为检验群落的异质性所设计的多样性指数，多年来沿着两个不同途径发展，一是应用统计抽样理论方法观察分析群落结构如何发生发展变化的, 如对数序列模型(Fisher et al.,1943)和对数正态分布模型(Preston, 1948)。

二是应用信息理论来评价群落结构的多样性，如Simpson 指数、Shannon指数。

两种方法的可应用性一直在争论之中，但都由于理论依据不够充分而谁也说服不了谁。

因此两大类方法目前都在应用着。

我们在此也都进行介绍。

生态位理论，自从MacArthur(1967)开拓性的工作以来，目前已是分析群落结构最有力的方法之一。

群落结构的分析，以及群落内竞争物种之间动态的互作的描述都离不开物种生态位参数的度量。

在DPS 数据处理平台上，我们提供了生态位宽度(niche breadth)和生态位重叠(niche overlap)指标的估计技术。