《火车转弯问题》PPT课件

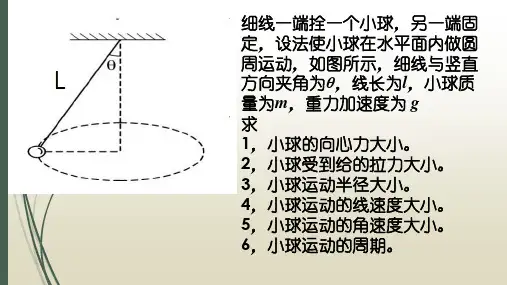
火车转弯问题考点规律分析甲乙(1)弯道的特点：在实际的火车转弯处，外轨高于内轨，若火车转弯所需的向心力完全由重力和支持力的合力提供，如图所示，即mgtanO=mR则v0=冷丽而，其中R为弯道半径，0为轨道平面与水平面间的夹角,v0为转弯处的规定速度。

(2)速度与轨道压力的关系①当火车行驶速度v等于规定速度v0时，所需向心力仅由重力和弹力的合力提供，此时火车对内外轨无挤压作用。

②当火车行驶速度v>v0时，火车对外轨有挤压作用。

③当火车行驶速度v<v0时，火车对内轨有挤压作用。

(3)注意事项①合外力的方向：因为火车转弯的圆周平面是水平面，不是斜面，所以火车的向心力即合外力应沿水平面指向圆心，而不是沿轨道斜面向下。

②规定速度的唯一性：火车轨道转弯处的规定速率一旦确定则是唯一的，火车只有按规定的速率转弯，内外轨才不受火车的挤压作用。

速率过大时，由重力、支持力及外轨对轮缘的挤压力的合力提供向心力；速率过小时，由重力、支持力及内轨对轮缘的挤压力的合力提供向心力。

典型例题例有一列质量为100t的火车，以72km/h的速率匀速通过一个内外轨一样高的弯道，轨道半径为400m。

(g取10m/s2)(1)试计算铁轨受到的侧压力大小；(2)若要使火车以此速率通过弯道，且使铁轨受到的侧压力为零，我们可以适当倾斜路基，试计算路基倾斜角度0的正切值。

［规范解答］(1)m=100t=1X105kg,v=72km/h=20m/s,夕卜轨对轮缘的侧内侧）、外侧压力提供火车转弯所需要的向心力厮以有林二m 牛二气晋N =1X 105N 。

由牛顿第三定律可知铁轨受到的侧压力大小为1X 105N 。

⑵火车过弯道,重力和铁轨对火车的支持力的合力正好提供向心力,如图所示，则mg tan 0二m 竺，由此可得tan 0=—=0.1。

［完美答案］（1）1X 105N （2）0.1一［规评点崗火车转弯（或赛道上赛车转弯）的圆轨道是水平轨道，所以合力的方向水平指向圆心。

图解法分析火车转弯问题问题的提出基本概念火车转弯时如果速度合适，铁轨就不会受到轮缘的侧向压力。

如果速度低于所要求的速度，内侧铁轨就会受到侧向挤压；如果速度高于所要求的速度，外侧铁轨就会受到侧向挤压。

这个结论需要高中生掌握，但这个结论的得出，我们不得不承认在一定程度上是凭的直觉。

本文试图用图解法来讨论这个问题。

在本文中，我们约定平行于铁轨所在平面的压力称为侧向压力；垂直于铁轨所在平面的压力称为正压力。

定性分析我们所要讨论的问题中轨道圆在水平面内，因此合力（向心力）的方向总是水平的。

另一方面，重力的大小和方向也总是不变的。

我们的讨论也是基于这两个不变性的：在图1中，火车的速度恰好符合要求，重力和支持力的合力提供火车做圆周运动的向心力。

若火车的速度减小，根据向心力的表达式Rv m F 2知向心力将减小。

然而重力是不变的，因此其他力的合力将变成图2中粉红色的有向线段所表示的力。

我们进一步分析这个力的分力：一是轨道对火车的垂直于轨道所在平面的力（正压力）；一是轨道对火车的平行于轨道所在平面的力（侧向压力）。

我们把这个粉红色的线段所表示的力分解到它的两个分力所在的方向，就得到了表示侧向压力的线段和正压力的线段（图2中鲜绿色线段）。

从图中可以看出，这时火车将受到一个沿轨道平重O N图1 图2图3图4面向上的侧向压力，并且它将随着速度的减小而增大（图4）。

另一方面，表示垂直于斜面的支持力（正压力）的线段比原来短了，表明支持力减小了，并且我们会看到，随着速度的减小，支持力将逐渐减小。

当火车的速度增大时（大于所要求的数值），用同样的方法（图3）可以得到：火车将受到一个沿轨道所在平面向下的侧向压力，并且随着速度的增大而增大（图4）。

另一方面，支持力将大于原来的支持力（图3），并且随着速度的增大而增大（图4）。

定量计算侧向压力的计算：首先我们先看速度较小时的情景，如图2所示，设轨道所在平面的倾角为θ，火车驶过转弯处没有侧向压力时的速度为0v 。

火车转弯问题考点规律分析(1)弯道的特点：在实际的火车转弯处，外轨高于内轨，若火车转弯所需的向心力完全由重力和支持力的合力提供，如图所示，即mg tanθ＝m v20R，则v0＝gR tanθ，其中R为弯道半径，θ为轨道平面与水平面间的夹角，v0为转弯处的规定速度。

(2)速度与轨道压力的关系①当火车行驶速度v等于规定速度v0时，所需向心力仅由重力和弹力的合力提供，此时火车对内外轨无挤压作用。

②当火车行驶速度v>v0时，火车对外轨有挤压作用。

③当火车行驶速度v<v0时，火车对内轨有挤压作用。

(3)注意事项①合外力的方向：因为火车转弯的圆周平面是水平面，不是斜面，所以火车的向心力即合外力应沿水平面指向圆心，而不是沿轨道斜面向下。

②规定速度的唯一性：火车轨道转弯处的规定速率一旦确定则是唯一的，火车只有按规定的速率转弯，内外轨才不受火车的挤压作用。

速率过大时，由重力、支持力及外轨对轮缘的挤压力的合力提供向心力；速率过小时，由重力、支持力及内轨对轮缘的挤压力的合力提供向心力。

典型例题例有一列质量为100 t的火车，以72 km/h的速率匀速通过一个内外轨一样高的弯道，轨道半径为400 m。

(g取10 m/s2)(1)试计算铁轨受到的侧压力大小；(2)若要使火车以此速率通过弯道，且使铁轨受到的侧压力为零，我们可以适当倾斜路基，试计算路基倾斜角度θ的正切值。

[规范解答](1)m＝100 t＝1×105 kg，v＝72 km/h＝20 m/s，外轨对轮缘的侧压力提供火车转弯所需要的向心力，所以有：F N ＝m v 2r ＝105×202400 N ＝1×105 N 。

由牛顿第三定律可知铁轨受到的侧压力大小为1×105 N 。

(2)火车过弯道，重力和铁轨对火车的支持力的合力正好提供向心力，如图所示，则mg tan θ＝m v 2r ，由此可得tan θ＝v 2rg ＝0.1。

1
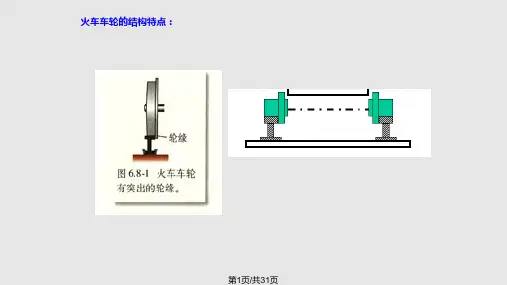
车轮与铁轨实物照片2
车轮与铁轨实物照片
车轮与铁轨实物照片
3
水平枕木时车轮与铁轨
受力分析示意图
水平枕木时列车转弯时
圆周平面图
水平枕木时列车转弯时受力分析等效图
水平枕木时列车转弯时F
2
弯时铁轨与车轮示意图枕木外高内低时列车转
1
弯时铁轨与车轮示意图
枕木外高内低时列车转
2
,圆周运动的平面示意图时枕木外高内低列车转弯
1
,,示意图圆周运动的平面列车转弯时
枕木外高内低
,,列车以临界速度转弯时枕木外高内低2
,,受力分析图列车以临界速度转弯时枕木外高内低
受力分析图
速度转弯时列车以大于临界枕木外高内低,,
受力分析图
速度转弯时列车以小于临界枕木外高内低,,。