中考压强压轴计算题带答案解析

一、初中物理压力与压强问题1．如图所示，甲、乙两个均匀实心正方体放在水平地面上时对水平地面的压强相等，若分别在两物体上沿竖直方向截去厚度相同的部分并分别叠放在对方剩余部分的上方，此时压强p 甲、p 乙比较，正确的是（ ）A ．可能是p 甲> p 乙B ．一定是p 甲> p 乙C ．可能是p 甲= p 乙D ．一定是p 甲< p 乙【答案】B 【解析】 【详解】甲、乙两个均匀实心正方体放在水平地面上时对水平地面的压强相等，则3G a 甲甲=3G a 乙乙，设a 甲=5cm ，a 乙=10cm ，截去厚度为2cm ， 则G 甲=18G 乙，叠放在对方剩余部分的上方后的压强p 甲=33251035G G a +甲乙甲=3G a 甲甲+313G a ⨯乙甲=3G a 甲甲+13×38G a 甲甲=3113G a ⨯甲甲 p 乙=382105810G G a +乙甲乙=3G a 乙乙+312G a ⨯甲乙=3G a 乙乙+12×318G a 乙乙=1716×3G a 乙乙 故p 甲> p 乙。

故选B 。

2．甲、乙两个实心均匀正方体放在水平地面上，他们对地面压强相等，已知ρ甲<ρ乙,在两个正方体上部分别沿水平方向切去相同的高度，切去部分的质量分别为m ′甲和m ′乙,则下列说法中正确的是 A ． m ′甲一定大于m ′乙 B ． m ′甲一定小于m ′乙 C ． m ′甲一定等于m ′乙 D ． m ′甲可能等于m ′乙【答案】A 【解析】 【详解】据最初压强相等有：ρ甲gh 甲=ρ乙gh 乙，ρ甲h甲=ρ乙h乙ρ甲<ρ乙，故:h甲>h乙。

甲的横截面积:S甲=h2甲，乙的横截面积:S乙=h2乙.设切去的高度为△h，要比较切去部分的质量，切去部分的质量=密度×切去部分的体积:m′甲=ρ甲S甲∆h=ρ甲h2甲∆h=ρ甲h甲h甲∆hm′乙=ρ乙S乙∆h=ρ乙h2乙∆h=ρ乙h乙h乙∆h则:m′甲>m′乙。

上海市中考物理压强压轴题：专题03 柱体切割后浸入液体中，无液体溢出一、常见题目类型1．将柱形物体沿水平方向切去某一厚度（体积或质量），并将切去部分浸没在容器的液体中（图1）。

2．将柱形物体沿竖直方向切去某一厚度（体积或质量），并将切去部分浸没在容器的液体中（图2）。

二、例题【例题1】如图1所示，均匀长方体甲和薄壁圆柱形容器乙置于水平地面上。

长方体甲的底面积为3S 。

容器乙足够高、底面积为2S ，盛有体积为5×10-3米3的水。

① 若甲的重力为20牛，底面积为5×10-4米2，求甲对地面的压强p 甲。

② 求乙容器中水的质量m 水。

③ 若将甲沿水平方向切去厚度为h 的部分，并将切去部分浸没在乙容器的水中时，甲对水平地面压强的变化量Δp 甲恰为水对乙容器底部压强增加量Δp 水的2倍。

求甲的密度ρ甲。

【答案】①40000帕；②5千克；③3×103千克/米3。

【解析】① F 甲=G 甲=20牛p 甲＝F 甲/S 甲＝20牛/5×104米2＝ 40000帕② m 水＝ρ水V 水＝1×103千克/米3×5×103米3＝5千克图1乙甲图1 乙甲甲乙图2③甲对水平地面压强的变化量Δp甲即为切去厚度为h部分的压强Δp甲＝ΔF甲/S甲＝甲gh水对乙容器底部压强增加量Δp水为水升高的高度h水＝3Sh/2SΔp水＝水g h水＝水g（3Sh/2S）因为Δp甲＝2Δp水甲gh ＝2水g（3Sh/2S）所以ρ甲＝3×103千克/米3【例题2】如图2所示，底面积为10-2米2、高为0.4米长方体甲（ρ甲＝2×103千克/米3）和底面积为2×10-2米2的薄壁柱形容器乙放在水平地面上。

乙容器足够高，内盛有0.1米深的水。

甲乙（1）求甲的质量m甲。

（2）求水对乙容器底部的压强p水。

（3）现沿水平方向将长方体甲截取一定的厚度，并将截取部分竖直放入乙容器中，使得水对容器底部的压强最大，且长方体甲对地面的压强减少量最小，请求出甲对地面的压强减少量。

一、初中物理压力与压强问题1．均匀实心正方体甲、乙对水平地面的压强相等。

已知它们的边长l 甲＞l 乙，现将两物体均沿水平方向切去一部分厚度∆h ，则（ ） A ．若切去相等体积，P’甲可能小于P’乙 B ．若切去相等体积，P’甲一定小于P’乙 C ．若切去相等质量，∆h 甲一定小于∆h 乙 D ．若切去相等质量，∆h 甲可能小于∆h 乙【答案】C 【解析】 【分析】 【详解】AB ．沿水平方向切去一部分厚度∆h ，且边长l 甲＞l 乙，利用极限思想，乙被切没了，甲还有剩余，所以剩下的甲的压强大于乙的压强，所以AB 错误； CD ．均匀实心正方体甲、乙对水平地面的压强相等，所以gL gL ρρ=甲甲乙乙根据上式可得L L ρρ=甲甲乙乙因为切去相等的质量，所以22L h L h ρρ∆=∆甲甲甲乙乙乙结合上式可得L h L h ∆=∆甲甲乙乙又因为l 甲＞l 乙，所以∆h 甲一定小于∆h 乙，所以C 正确，D 错误。

故选C 。

2．如图所示，甲、乙是放在水平地面上的两个质量均匀的长方体，它们的密度之比:2:3ρρ=甲乙，底面积之比:3:4S S =甲乙，对水平地面的压强之比:8:5p p =甲乙，下列有关甲、乙的说法正确的是（ ）A ．甲、乙的重力之比是1∶2B ．甲、乙的体积之比是16∶5C ．甲、乙的高度之比是5∶12D ．将甲、乙分别沿水平方向切去相同的高度后，甲剩余部分对地面的压强大于乙剩余部分对地面的压强 【答案】D 【解析】 【分析】【详解】A ．甲、乙是放在水平地面上的两个质量均匀的长方体，它们的重力之比为836545G F p S p S G F p S p S ===⨯=⨯=甲甲甲甲甲甲乙乙乙乙乙乙故A 错误；B ．甲、乙的体积之比是639525G m gV G m G V G gρρρρρρ===⨯=⨯=甲甲甲甲甲甲乙乙乙乙乙甲乙乙故B 错误；C ．甲、乙的高度之比是9412535V h S V S V h V S S ==⨯=⨯=甲甲甲甲乙乙乙乙甲乙故C 错误；D ．将甲、乙分别沿水平方向切去相同的高度后，甲剩余部分对地面的压强大于乙剩余部分对地面的压强之差为122221212()()gV gV F F G G m g m g p p gh gh g h h g h h S S S S S S S S ρρρρρρ-=-=-=-=-=-=---甲乙111甲乙甲甲乙乙12121212由于:2:3ρρ=甲乙所以23ρρ=甲乙 由于125h h =甲乙 所以125h h =甲乙 故12212291()()0353153p p g h h g h h g h gh gh gh gh gh ρρρρρρρρ-=---=⨯--+=+>甲甲乙乙乙乙乙乙乙乙乙乙乙所以12p p >故D 正确。

专题05 在容器里加物体后,有液体溢出一、常见题目类型1．将物体甲浸没在柱形容器乙的液体中（图1）。

2．将物块丙放入容器甲的液体中、叠放在柱体乙的上方（图2）。

3．将甲、乙两个实心均匀光滑小球先后分别放入容器中（图3). 4．在柱形物体乙上方沿水平方向切去一部分，并将切去部分竖直放在甲容器内（浸没或不浸没）(图4）.二、例题【例题1】柱形轻质薄壁容器的底面积为1×10—2米2，如图1所示,甲图4图3 乙图1甲乙甲乙图2丙内盛0。

2米深度的水后置于水平地面上。

① 求容器底部受到水的压强p 水。

② 现将一块质量为1.5千克、体积为1×10—3米3的物体完全浸没在容器的水中后，测得容器底部受到水的压强为2450帕。

求此时容器对水平桌面的压强p 容。

【答案】①1960帕;②2940帕。

【解析】 ①p 水=ρ水g h=1×103千克/米3×9.8牛/千克×0.2米3=1960帕②物体浸没在容器的水中后,容器底部受到水的压强为2450帕可求现在水的深度h ＇：p ＇水=ρ水g h ＇ h ＇= p ＇/ρ水gh ＇=2450帕/1×103千克/米3×9。

8牛/千克=0。

25米容器内剩余水的体积为V 剩余水= S h ＇－V 物=0。

25米×1×10—2米2－1×10-3米3=1。

5×10-3米3现在容器对水平桌面的压力图1F 容=G 容=（m 剩余水＋m 物）g=（1。

5×10—3米3×1×103千克/米3＋1.5千克)×9.8牛/千克=29.4牛对水平桌面的压强P 容= F 容/S =29。

4牛/ 1×10-2米2=2940帕(注意：此题不计算溢出水的质量,更简单。

也可用其他方法求解） 【例题2】如图2所示，盛有水的轻质薄壁圆柱形容器甲和实心均匀圆柱体乙均放置于水平地面上,它们的底面积分别为1×10-2米2和0.5×10—2米2.现将两完全相同物块分别放入容器甲中和叠在圆柱体乙的上方，放置前后容器甲、圆柱体乙对水平地面的压强大小p 甲、p 乙如下表所示。

一、初中物理压力与压强问题1．如图所示，水平桌面上放着相同的两个平底试管A 和B ，其中分别装着密度不同的液体，A 管竖直放罝，B 管倾斜放置，它们对管底的压强p A 等于p B ，则下列关于液体质量m A 和m B 判断正确的是（ ）A ．m A >mB B ．m A =m BC ．m A <m BD ．条件不足，无法判断【答案】C 【解析】 【分析】 【详解】当B 管竖直放罝时，高度会变高，根据液体压强公式p gh ρ=可知'B B p p <，由已知A B p p =，可得'A B p p <，两个平底试管A 和B 是相同的，底面积也相同，'A B p p <两边乘上底面积S ，可得'A B p S p S <即两个平底试管A 和B 受到液体的压力'A B F F <，而这两个压力就是对应液体的重力，即A B G G <，A B m m <，故选C ．2．两个正方体甲乙放在水平地面上，它们对水平面的压强相等，沿水平方向切去不同厚度，使剩余的厚度相同，剩余的压力相同，则甲乙切去的质量Δm 甲、Δm 乙和甲乙的密度满足的关系是（ ）A ．ρ甲＞ρ乙，Δm 甲＞Δm 乙B ．ρ甲＜ρ乙，Δm 甲＞Δm 乙C ．ρ甲＜ρ乙，Δm 甲＜Δm 乙D ．ρ甲＞ρ乙，Δm 甲＜Δm 乙【答案】D 【解析】 【分析】 【详解】正方体对水平地面的压强mg F G Vg gSh p gh S S S S Sρρρ====== 切割之前它们对水平面的压强相等p p =甲乙即gh gh ρρ=甲甲乙乙由图可知h h 甲乙＜所以ρρ甲乙＞由图知S 甲乙＜S在切割之前p p =甲乙所以由F pS =可知，切割之前甲、乙对地面的压力F F 甲乙＜因为正方体对水平地面的压力等于其重力，且G mg =，所以，切割之前m m 甲乙＜当沿水平方向切去不同厚度，剩余的压力相同，即F F =甲剩乙剩则甲、乙剩余部分的质量m m =甲剩乙剩根据切去的质量-m m m ∆=剩得m m ∆∆甲乙＜故D 正确，ABC 错误； 故选D 。

物理中考冲刺——压强压轴题分析例1：把一个密度均匀的圆柱体甲和装有适量的某液体的圆柱形容器乙平放在水平桌面上，如图所示，它们的底面积之比S甲：S乙＝3：4，对桌面的压强之比p甲：p 乙＝4：1．若在圆柱体甲上沿水平方向截取一段高为8cm的物体，并平稳放入容器乙中，施加一个外力使物体刚好浸没在深度为h乙的液体中（物体不与容器乙接触，液体无溢出），此时甲对桌面的压强p′甲＝12p甲，乙对桌面的压强p′乙＝2p乙且p′甲＝p′乙．则此时圆柱体甲对桌面的压强p′甲为（）Pa，物体浸没在液体后，容器乙中液体的深度h′乙是（）m（ρ甲＝1.2×103kg/m3，容器乙的壁厚和质量均忽略不计，g取10N/kg）。

分析：（1）我们要求在甲圆柱体在水平方向截取8cm后，对水平地面的压强，我们知道均匀柱体放在水平面上时，物体的压力和自身的重力相等，则圆柱体对水平桌面的压强p＝F/S＝G/S＝mg/S＝ρVg/S＝ρShg/S＝ρgh，我们只需求截取后圆柱体的高度即可；在圆柱体甲上沿水平方向截取一段高为8cm的物体后，甲对桌面的压强p甲′＝12p甲，据此求出圆柱体甲截取后的高度，利用p=F/S ＝ρgh求出此时圆柱体甲对桌面的压强；（2）容器乙的壁厚和质量均忽略不计，圆柱体容器对桌面的压强等于液体对容器底部的压强，根据p＝ρgh结合p乙′＝2p乙求出两者的液面高度关系，根据截取部分物体刚好浸没在乙液体中和V＝Sh求出液体原来的深度，进一步求出物体浸没后的深度。

解答：（1）因水平面上物体的压力和自身的重力相等，所以，圆柱体对水平桌面的压强：p甲＝F甲/S甲＝G甲/S甲＝m甲g/S甲＝ρ甲V甲g/S甲＝ρ甲S甲h甲g/S甲＝ρ甲gh甲，在圆柱体甲上沿水平方向截取一段高为8cm的物体后，甲对桌面的压强p甲′＝12p甲，则ρ甲g（h甲0.08m）＝12ρ甲gh甲，解得：h甲＝0.16m＝16cm，所以，此时圆柱体甲对桌面的压强：p甲′＝ρ甲g（h甲0.08m）＝1.2×103kg/m3×10N/kg×（0.16m0.08m）＝960Pa；（2）容器乙的壁厚和质量均忽略不计，因圆柱体容器对桌面的压强等于液体对容器底部的压强，且p乙′＝2p乙，所以，由pe＝ρgh可得，h乙′＝2h乙，又因截取部分物体刚好浸没在乙液体中，所以，S乙h乙＋S甲×8cm＝2S乙h乙，则h乙＝S甲S乙×8cm＝34×8cm＝6cm，所以，h乙′＝2h乙＝2×6cm＝12cm＝0.12m 故答案为：960；0.12。

一、初中物理压力与压强问题1．如所示，一密度均匀的实心物块放在地面上，对地面的压强为p，若沿虚线将该物块切去一部分，留下部分对地面的压强为p'，则（）A．p < p' B．p > p' C．p= p' D．无法判断【答案】B【解析】【详解】设原来物体的重力为G原，梯形的下表面积为S1；给原来的物体增加G部分的物体，如图所示，成为规则物体，那么，整个物体对地面的压强为：1111G G G G Gp pS S S S+==+=+原原总；沿虚线将该物块切去一部分，设此时剩余部分的重力为G＇，梯形的下表面积为S2，根据第一幅图的情况可知，质量和面积是等比例减小的，所以总压强是不变的。

根据关系可知：G G G G Gp pS S S S+==+=+总２２２２＇＇＇；根据p总相等可得：1G Gp pS S+=+２＇那么：1G Gp pS S=２－＇－＞０所以：p＞p′；故选B。

2．如图所示，两个相同的柱形容器置于水平地面，容器中分别盛有相等体积的不同液体甲、乙。

取两块质量相同的橡皮泥，将一块橡皮泥撑开成碗状放入甲液体中，将另一块捏成球形状放入乙液体中，橡皮泥静止后如图所示。

以下判断正确的是（）A ．橡皮泥受到的浮力 F 甲=F 乙B ．液体对容器底部的压强 p 液甲＜p 液乙C ．液体的密度ρ甲＞ρ乙D ．容器对地面的压强 p 地甲＞p 地乙【答案】A 【解析】 【分析】 【详解】A ．橡皮泥在甲液体中漂浮，橡皮泥受到的浮力F 甲=G ，橡皮泥在乙液体中悬浮，橡皮泥受到的浮力F 乙=G ，所以F 甲=F 乙，故A 符合题意；B C ．两个相同的柱形容器置于水平地面，容器中分别盛有相等体积的不同液体甲、乙，当放入橡皮泥后，液面仍然相平，说明橡皮泥排开甲、乙两种液体的体积是相同的，由于橡皮泥受到的浮力F 甲=F 乙，则=V g V g ρρ甲乙甲排乙排=ρρ甲乙液体甲、乙对容器底部的压强分别为=p gh ρ甲甲液甲 =p gh ρ乙乙液乙由于=ρρ甲乙，=h h 甲乙所以=p p 液甲液乙，故B 、C 错误； D ．容器对面的压强分别为G G F p S S +==液甲甲容地甲 G G F p S S+==液乙容乙地乙 由于液体甲、乙的体积相同，密度相同，所以液体甲、乙的质量相同，重力也相同，所以p p =地甲地乙故D 错误。

一、初中物理压力与压强问题1.如图所示，甲、乙两个实心均匀正方体静止在水平而上，甲对水平面的压强比乙小，下列方案中一定能使甲对水平而压强大于乙的有L期rn n ।方案：①将甲沿竖直方向切去一半，并将切去部分叠放在甲剩余部分上方②将乙沿竖直方向切去一半，并将切去部分叠放在甲的上方③将乙沿水平方向切去一半，并将切去部分叠放在甲的上方A. 0个B. 1个C. 2个D. 3个【答案】B【解析】【详解】①将甲沿竖直方向切去一半，并将切去部分叠放在甲剩余部分上方,此时甲对地面的压力不变，受力而积变为原来的二分之一，根据公式p=二可知甲对地面的压强变为原来的25倍，而乙对地而的压强没变，甲对水平而压强不一定大于乙对水平而压强；②将乙沿竖直方向切去一半，并将切去部分叠放在甲的上方，此时因为乙对地面的压力和受力面积都变为了原来的二分之一，根据公式P=£可知乙对地而的压强不变，而对甲来S说受力面积没变，压力增大，所以甲对地面的压强增大，但甲对水平面压强不一定大于乙对水平而压强：③将乙沿水平方向切去一半，并将切去部分叠放在甲的上方，此时乙对地面的压力变为原来的二分之一，而受力面积不变，根据公式可知乙对地面的压强将变为原来的二分之一.甲此时对地面的压力为! G/. + G中大于乙对地面的压力，而甲与地面的接触面枳小于2乙跟地而的受力而积，所以根据P=-可知甲对水平而压强一定大于乙对水平面的压强.S故选B.2.如所示，一密度均匀的实心物块放在地而上，对地面的压强为p,若沿虚线将该物块切去一部分，留下部分对地面的压强为P',则（）A. p<p'B. p> p C・P=P' D.无法判断【答案】B【解析】【详解】设原来物体的重力为G %,梯形的下表面积为Si；给原来的物体增加G部分的物体，如图所示，成为规则物体，那么，整个物体对地面的压强为：G|Q +G G. G Gp =- ...... = = p + —忘■■S、 5沿虚线将该物块切去一部分，设此时剩余部分的重力为G，,梯形的下表面积为S2,根据第一幅图的情况可知，质量和而积是等比例减小的，所以总压强是不变的。

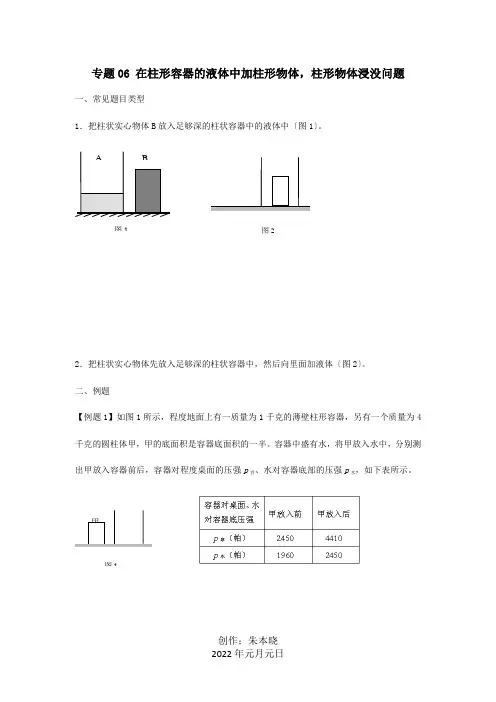
专题06 在柱形容器的液体中加柱形物体，柱形物体浸没问题一、常见题目类型1．把柱状实心物体B 放入足够深的柱状容器中的液体中〔图1〕。

2．把柱状实心物体先放入足够深的柱状容器中，然后向里面加液体〔图2〕。

二、例题【例题1】如图1所示，程度地面上有一质量为1千克的薄壁柱形容器，另有一个质量为4千克的圆柱体甲，甲的底面积是容器底面积的一半。

容器中盛有水，将甲放入水中，分别测出甲放入容器前后，容器对程度桌面的压强p 容、水对容器底部的压强p 水，如下表所示。

图1图2图1①求圆柱体甲放入容器前水的深度。

②求容器的底面积。

③放入圆柱体甲后，通过计算判断柱形容器的水是否有溢出。

④请判断甲在水中的状态并说明理由〔提示：漂浮、浸没、未浸没等〕。

⑤求圆柱体甲的密度。

【答案】①0.2米；②2×102米2 ；③无水溢出；④浸没；⑤4×103千克/米3。

【解析】①h水＝p水前/ρ水g＝1960帕/〔1×103千克/米3×/千克〕＝②p＝p容前－p水前＝F/ S容＝G容/ S容S容＝G容/p＝〔1千克×/千克〕/〔2450帕－1960帕〕＝2×102米2③甲放入水中，容器对程度桌面增大的压力F容=p S容=〔4410帕-2450帕〕×2×102米2F容=G甲，所以无水溢出。

④因为p容>p水，所以圆柱体甲在水中一定沉底，且S甲=S/2，p水后<2p 水前，所以甲在水中一定浸没〔假设未浸没时，S甲=S/2，后来水的深度h水后=2h水前，p水后=2p 水前〕。

⑤因为F容=G甲，所以无水溢出h水＝p水/ρ水g＝490帕/1×103千克/米3×/千克＝V甲＝V排＝S 容h水＝2×102米2＝1×103米3ρ甲＝m甲/V甲＝4千克/ 1×103米3＝4×103千克/米3【例题2】如图2所示，程度桌面上放有轻质圆柱形容器A〔容器足够高〕和实心圆柱体B。

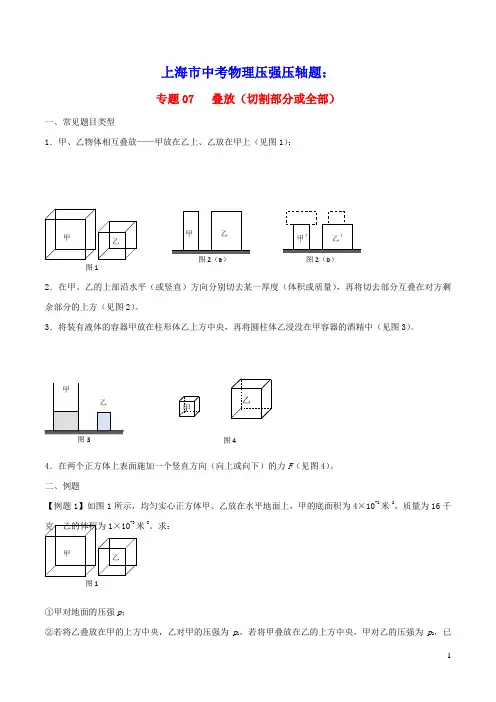
上海市中考物理压强压轴题：专题07 叠放（切割部分或全部）一、常见题目类型1．甲、乙物体相互叠放——甲放在乙上、乙放在甲上（见图1）：2．在甲、乙的上部沿水平（或竖直）方向分别切去某一厚度（体积或质量），再将切去部分互叠在对方剩余部分的上方（见图2）。

3．将装有液体的容器甲放在柱形体乙上方中央，再将圆柱体乙浸没在甲容器的酒精中（见图3）。

4．在两个正方体上表面施加一个竖直方向（向上或向下）的力F （见图4）。

二、例题【例题1】如图1所示，均匀实心正方体甲、乙放在水平地面上，甲的底面积为4×10-2米2，质量为16千克，乙的体积为1×10-3米3。

求：①甲对地面的压强p ；②若将乙叠放在甲的上方中央，乙对甲的压强为p 1，若将甲叠放在乙的上方中央，甲对乙的压强为p 2，已甲乙图1图3图4甲乙甲乙图1图2（b ）图2（a ）知p2＝4p1。

求乙的密度。

③当甲、乙分别平放在水平地面上时，若分别沿水平方向切去相同的体积V，则求甲、乙对地面压强变化量△p甲与△p乙的比值。

【答案】①3920pa；②4103 kg/m3；③1/8。

【解析】① p甲＝F甲/S甲＝G甲/S甲＝16kg 9.8N/kg/4102m2＝3920pa②将乙叠放在甲的上方中央，乙对甲的压强为p1 = F乙/S乙＝ G乙/S乙将甲叠放在乙的上方中央，甲对乙的压强为p2= G甲/S乙因为p2＝4p1即G甲/S乙＝4G乙/S乙所以 G甲＝4G乙m甲g＝4ρ乙gV乙ρ乙＝m甲/4V乙＝16kg/4103 m3＝4103 kg/m3③甲的密度ρ甲＝m甲/V甲＝16kg/8×10-3m3＝2×103kg/m3甲、乙密度之比：ρ甲/ρ乙＝1/2，甲、乙底面积之比：S甲/ S乙=4/1当沿水平方向切去相同的体积V时，甲、乙切去的厚度之比：△h甲：△h乙=V/ S甲：V/ S乙=1:4甲、乙对地面压强变化量△p甲与△p乙的比值△p甲/△p乙=ρ甲gh甲/ρ乙gh乙=1/8【例题2】如图2所示，薄壁圆柱形容器甲和圆柱体乙均放置在水平地面上。

（物理）中考物理压强试题(有答案和解析)一、压强1．如图所示，A、B、C是三个圆柱形容器，分别装有水或酒精（ρ酒精＜ρ水），A、C两容器中液体深度相同，B、C两容器的底面积相同．三个容器底部所受的液体压强分别为p A、p B、p C，则下列判断正确的是A．p A＞p B＞p CB．p C＜p A=p BC．p B＞p A=p CD．p C＜p A＜p B【答案】D【解析】【详解】液体压强与液体密度及液体深度有关，液体压强公式p=ρgh，A、C两容器中液体深度相同，A容器中装有水，C容器内装有酒精，又ρ酒精＜ρ水，故p C＜p A；A、B两容器都装水，但容器B内的水比容器A内的水深度较深，可得p A＜p B．综上所述三个容器底部所受的液体压强大小关系为p C＜p A＜p B；故答案选D．2．对下列现象解释正确的是A．蚊子尖尖的口器，可以增大压力B．液体从容器侧壁的孔喷出，说明液体对容器底有压强C．用吸管吸饮料，利用大气压把饮料“吸”入口中D．口吹硬币跳越木块，利用流体流速大的位置压强大的原理【答案】C 【解析】 【分析】（1）增大压强的方法：在压力一定时，减小受力面积来增大压强；在受力面积一定时，增大压力来增大压强．（2）由于液体受到重力作用，且具有流动性，所以液体对容器底和容器侧壁有压强； （3）吸管吸饮料时，在外界大气压的作用下，饮料被压进吸管里；（4）流体的压强与流速的关系：流体在流速大的地方压强小、在流速小的地方压强大． 【详解】A ．蚊子有尖尖的口器，是在压力一定时，通过减小受力面积来增大压强．故A 错误；B ．液体从容器侧壁的孔喷出，说明液体对容器侧壁有压强．故B 错误；C ．用吸管吸饮料时，先把吸管内的空气吸走，管内气压减小，在外界大气压的作用下，饮料被压入人的口中，利用大气压，故C 正确；D ．在硬币上方沿着与桌面平行方向用力吹一口气，硬币上方气流速度大于下方的气流速度，硬币上方的气体压强小于下方的气体压强，从而产生向上的“升力”，所以，口吹硬币跳越木块，利用了流体在流速大的位置压强小的原理．故D 错误． 【点睛】本题是事例都是生活中的常用的现象，利用生活现象考查物理知识，体现物理和生活的密切关系，体现了学以致用的目的．3．有甲、乙两个完全相同的密闭圆台形容器一正一反放置在同一水平桌面上，甲、乙容器内装有质量不相等的同种液体，且两容器内液体的液面相平，如图所示。

〔d 〕压强计算题〔教师版）1〔崇明）、米2,内装有0.3米深的水，求：〔1）容器内水的质量m 水； 〔2）容器内水对底部的压强F 水；〔3）假设将体积为8x10-3米3的正方体B 轻轻放入A 容器中，此时：容器内水对底部的压 强变化量为，容器对水平地面的压强变化量M •请通过计算比较M 和的M 大小关系 及对应的正方体B 的密度.〔本小题可直接写出答案，无需解题过程）〔图 12）解.〔1） m zK=p 水V=1000千克/米'米'=30千克3分〔2）p 水=p 4<gh =1. 0X103千克/米 3X9. 8 牛/千克X0. 3 米= 2940 帕 3 分 〔3） P B 小于或等于水的密度〔或1000千克/米3）时，APi 等于AP21分P B 大于水的密度〔或1000千克/米3）时，APi小于AP22. 〔虹口〕如图12所示，质量为2千克的实心正方体放置在水平地面上。

① 假设该正方体的体积为1X10-3米3,求它的密度p 和对地面的压强Q 。

② 假设该正方体的边长为/,现沿竖直方向切去厚度为△/的部分甲，如图13〔a 〕所示, 然后将切去部分旋转90度后叠放在剩余部分乙的上外表的中央，如图13〔b 〕、〔c 〕、〔d 〕 所示。

此时甲对乙的压强和乙对地面的压强分别为P 甲、P 乙,请通过推导得出R 甲与P 乙的 大小关系及△/的取值范围。

■--------------- A ------------------------■〔a 〕〔乙③ 当P甲二P乙P甲gh件P水gh水P甲g 〔h竹h〕= ■水g（h料h）1分2（0.1m-h）=0.1m+hh=l/30m=0.033m 1 分乙容器中h最大・'.不可能出现p甲=p乙.••当0VhW0.02m p伊〉p乙1分13.如图13所示，轻质圆柱形容器A内装有部分水，实心圆柱体B放在水平桌面上, 〔1）假设A容器中水的质量为2千克，求水的体积1/水。

一、初中物理压力与压强问题1．如图所示，水平地面上的柱体 A、B 高度相等，其底面积 S 的大小关系为 S A＞S B．现分别从两柱体的上表面沿竖直方向往下切除部分后，发现 A、B 剩余部分对地面的压力、压强恰好均相等．则关于对切去部分的质量△m A、△m B以及底面积△S A、△S B的判断，正确的是（）A．△S A＞△S B，△m A=△m B B．△S A＞△S B，△m A＞△m BC．△S A＜△S B，△m A＞△B D．△S A＜△S B，△m A＜△m B【答案】B【解析】【分析】【详解】因为p＝F G mg Vg SghS S S S Sρρ＝＝＝＝＝ρgh，柱体 A、B 高度相等，且分别从两柱体的上表面沿竖直方向往下切除部分后，A、B 剩余部分对地面的相等，所以有：ρA gh＝ρB gh，故ρA＝ρB，水平地面上的柱体对地面的压力等于其重力，即F＝G，根据G＝mg、ρ＝可得，切去部分后A、B 剩余部分对地面的压力相等，所以有：ρA（S A﹣△S A）gh＝ρB（S B﹣△S B）gh，则S A﹣△S A＝S B﹣△S B，又因为S A＞S B，所以，△S A＞△S B，故CD错误；因为S A＞S B，柱体 A、B 高度相等，所以A的体积大于B的体积，又因为ρA＝ρB，所以，m A＞m B，切去部分后A、B 剩余部对地面的压力相等，所以有：（m A﹣△m A）g＝（m B﹣△m B）g，即m A﹣△m A＝m B﹣△m B，所以，△m A＞△m B，故A错误，B正确．故选B．2．如图所示，两个相同的柱形容器置于水平地面，容器中分别盛有相等体积的不同液体甲、乙。

取两块质量相同的橡皮泥，将一块橡皮泥撑开成碗状放入甲液体中，将另一块捏成球形状放入乙液体中，橡皮泥静止后如图所示。

以下判断正确的是（）A．橡皮泥受到的浮力F甲=F乙B．液体对容器底部的压强p液甲＜p液乙C．液体的密度ρ甲＞ρ乙D．容器对地面的压强p地甲＞p地乙【答案】A【解析】【详解】A ．橡皮泥在甲液体中漂浮，橡皮泥受到的浮力F 甲=G ，橡皮泥在乙液体中悬浮，橡皮泥受到的浮力F 乙=G ，所以F 甲=F 乙，故A 符合题意；B C ．两个相同的柱形容器置于水平地面，容器中分别盛有相等体积的不同液体甲、乙，当放入橡皮泥后，液面仍然相平，说明橡皮泥排开甲、乙两种液体的体积是相同的，由于橡皮泥受到的浮力F 甲=F 乙，则=V g V g ρρ甲乙甲排乙排=ρρ甲乙液体甲、乙对容器底部的压强分别为=p gh ρ甲甲液甲=p gh ρ乙乙液乙由于=ρρ甲乙，=h h 甲乙所以=p p 液甲液乙，故B 、C 错误； D ．容器对面的压强分别为G G F p S S+==液甲甲容地甲G G F p S S+==液乙容乙地乙由于液体甲、乙的体积相同，密度相同，所以液体甲、乙的质量相同，重力也相同，所以p p =地甲地乙故D 错误。

一、初中物理压力与压强问题1．如图所示，A 、B 两立方体叠置在一起放于水平桌面上，A 的密度为ρA ，B 的密度为ρB 且ρA ∶ρB =1∶2，开始时它们的边长比为L A ∶L B =1∶1，若不断地缩小A 立方体的体积，但始终保持A 的形状为立方体，使A 、B 两立方体的边长L A ∶L B 的比值由1∶1逐渐变为1∶2、则压强p A ∶p B 的比值变化情况为（ ）A ．始终变大B ．始终变小C ．先减小后变大D ．先增大后减【答案】B 【解析】 【分析】根据A 、B 两立方体的边长之比求出面积、体积之比；因放在水平面上物体对支持面的压力大小等于物体重力的大小，所以根据密度公式和压强公式求出A 对B 的压强与B 对桌面的压强之比，当不断地缩小A 立方体的体积时，根据特殊值法判断比值的变化情况。

【详解】由 L A ∶L B =1∶1可知S A ∶S B =1∶1， V A ∶V B =1∶1由ρA ：ρB =1∶2可知m A ∶m B =1∶2又因为A 、B 两立方体叠放在一起放在水平桌面上，根据压强公式Fp S=可得 A A B A B A B B B A A B A A B A 1()()3p F S G S m gS p F S G G S m g m g S ====++ 若不断地缩小A 立方体的体积时，设L′A ∶L B =k ，且112k ≤≤，则有 S′A ∶S B =k 2， V′A ∶V B = k 3由ρA ∶ρB =1∶2可知3A B 12m m k '=: 则有A AB A B A B 3B B AA B A A B A ()()2p F S G S m gS k p F S G G S m g m g S k ''''====''''''+++当1k =时，A B :1:30.333p p =≈； 当0.9k =时，A B :0.330p p ≈；当0.8k =时，A B :0.318p p ≈； 当0.7k =时，A B :0.300p p ≈； 当0.6k =时，A B :0.271p p ≈； 当0.5k =时，A B :0.235p p ≈；故不断地缩小A 立方体的体积时，压强p A ∶p B 的比值变化情况为始终变小。

一、初中物理压力与压强问题1．如图所示，A 、B 两立方体叠置在一起放于水平桌面上，A 的密度为ρA ，B 的密度为ρB 且ρA ∶ρB =1∶2，开始时它们的边长比为L A ∶L B =1∶1，若不断地缩小A 立方体的体积，但始终保持A 的形状为立方体，使A 、B 两立方体的边长L A ∶L B 的比值由1∶1逐渐变为1∶2、则压强p A ∶p B 的比值变化情况为（ ）A ．始终变大B ．始终变小C ．先减小后变大D ．先增大后减【答案】B 【解析】 【分析】根据A 、B 两立方体的边长之比求出面积、体积之比；因放在水平面上物体对支持面的压力大小等于物体重力的大小，所以根据密度公式和压强公式求出A 对B 的压强与B 对桌面的压强之比，当不断地缩小A 立方体的体积时，根据特殊值法判断比值的变化情况。

【详解】由 L A ∶L B =1∶1可知S A ∶S B =1∶1， V A ∶V B =1∶1由ρA ：ρB =1∶2可知m A ∶m B =1∶2又因为A 、B 两立方体叠放在一起放在水平桌面上，根据压强公式Fp S=可得 A A B A B A B B B A A B A A B A 1()()3p F S G S m gS p F S G G S m g m g S ====++ 若不断地缩小A 立方体的体积时，设L′A ∶L B =k ，且112k ≤≤，则有 S′A ∶S B =k 2， V′A ∶V B = k 3由ρA ∶ρB =1∶2可知3A B 12m m k '=: 则有A AB A B A B 3B B AA B A A B A ()()2p F S G S m gS k p F S G G S m g m g S k ''''====''''''+++当1k =时，A B :1:30.333p p =≈； 当0.9k =时，A B :0.330p p ≈；当0.8k =时，A B :0.318p p ≈； 当0.7k =时，A B :0.300p p ≈； 当0.6k =时，A B :0.271p p ≈； 当0.5k =时，A B :0.235p p ≈；故不断地缩小A 立方体的体积时，压强p A ∶p B 的比值变化情况为始终变小。

一、初中物理压力与压强问题1．如图（a ）所示，底面积不同的圆柱形容器分别盛有甲、乙两种液体，其密度为ρ甲和ρ乙。

已知液体对各自容器底部的压强相等。

现将甲、乙液体互换容器（均不溢出），如图（b ）所示，甲、乙液体对容器底部压强的变化量分别为Δp 甲、Δp 乙，则（ ）A ．ρ甲＞ρ乙，Δp 甲＞Δp 乙B ．ρ甲＜ρ乙，Δp 甲＜Δp 乙C ．ρ甲＜ρ乙，Δp 甲＝Δp 乙D ．ρ甲＞ρ乙，Δp 甲＝Δp 乙 【答案】A 【解析】 【详解】液体对各自容器底部的压强相等，即p p =甲乙，即gh gh ρρ=甲甲乙乙从图(a)可以看到，h h <甲乙，那么可知ρρ甲乙>现将甲、乙液体互换容器，那么可得''p gh ρ=甲甲甲、''p gh ρ=乙乙乙，甲、乙液体对容器底部压强的变化量分别为()'''p p p gh gh g h h ρρρ∆=-=-=-甲甲甲甲甲甲甲甲甲甲 ()'''p p p gh gh g h h ρρρ∆=-=-=-乙乙乙乙乙乙乙乙乙乙还可以知道甲液体、乙液体在大底面积1S 和小底面积2S 的容器中时的体积关系式是''12V V S h S h ===甲甲甲甲 ''21V V S h S h ===乙乙乙乙式子变换可以得到'21S h h S =⋅甲甲，'12S h h S =⋅乙乙，代入上面的式子可以得到 '''21211S S S p g h h gh S S ρρ⎛⎫-∆=-⋅=⋅ ⎪⎝⎭甲甲甲甲甲甲'''11222S S S p g h h gh S S ρρ⎛⎫-∆=-=⋅ ⎪⎝⎭乙乙乙乙乙乙两式相减可得到()''''211212121212-----h S h S S S S S p p gh gh g S S S S S S ρρρρ-∆∆=⋅⋅=⋅甲甲乙乙甲乙甲甲乙乙因为p p =甲乙，12S S >，那么12p S p S >甲乙即在(a)图甲液体对容器底的压力大于乙液体对容器底的压力，也可知G G >甲乙因为'2G h S ρ=甲甲甲、'1G h S ρ=乙乙乙，可知''21-0h S h S ρρ>甲甲乙乙所以-0p p ∆∆>甲乙即p p ∆>∆甲乙；故选A 。