周期矩形信号的频谱分析

信号与系统实验报告学院：电子信息与电气工程学院班级: 13级电信<1>班学号: *************:***实验六 矩形脉冲信号的分解 一、实验目的1. 分析典型的矩形脉冲信号，了解矩形脉冲信号谐波分量的构成；2. 观察矩形脉冲信号通过多个数字滤波器后，分解出各谐波分量的情况。

二、实验原理1. 信号的频谱与测量信号的时域特性和频域特性是对信号的两种不同的描述方式。

对于一个时域的周期信号)t (f ，只要满足狄利克莱(Dirichlet)条件，就可以将其展开成三角形式或指数形式的傅里叶级数。

例如，对于一个周期为T 的时域周期信号)t (f ，可以用三角形式的傅里叶级数求出它的各次分量，在区间)1,1(T t t +内表示为：)sin cos 1(0)(t n n b t n n n a a t f Ω+Ω∑∞=+=-----（1） 即将信号分解成直流分量及许多余弦分量和正弦分量，研究其频谱分布情况。

AA（c）图6-1 信号的时域特性和频域特性信号的时域特性与频域特性之间有着密切的内在联系，这种联系可以用图6-1来形象地表示。

其中图6-1(a)是信号在幅度--时间--频率三维座标系统中的图形；图6-1(b)是信号在幅度--时间座标系统中的图形即波形图；把周期信号分解得到的各次谐波分量按频率的高低排列，就可以得到频谱图。

反映各频率分量幅度的频谱称为振幅频谱。

图6-1(c)是信号在幅度--频率座标系统中的图形即振幅频谱图。

反映各分量相位的频谱称为相位频谱。

在本实验中只研究信号振幅频谱。

周期信号的振幅频谱有三个性质：离散性、谐波性、收敛性。

测量时利用了这些性质。

从振幅频谱图上，可以直观地看出各频率分量所占的比重。

测量方法有同时分析法和顺序分析法。

同时分析法的基本工作原理是利用多个滤波器，把它们的中心频率分别调到被测信号的各个频率分量上。

当被测信号同时加到所有滤波器上，中心频率与信号所包含的某次谐波分量频率一致的滤波器便有输出。

X
第
3.3.2 周期矩形脉冲信号的频谱
本小节以周期矩形脉冲信号为例进行分析
7 页
主要讨论：频谱的特点，频谱结构，
频带宽度，能量分布。
X
第
一．频谱结构
f (t ) E
8 页
脉宽为 脉冲高度为E
T1
t
T1
O 2 2
周期为T1
1. 三角函数形式的谱系数 2. 指数函数形式的谱系数 3. 频谱特点

2
0
2


n 1
X
不变， T1改变
E 2π T1 幅度 , 谱线 间隔1 T1 T1
f (t )
2π 第一个过零点频率 不变
第 13 页
当ET1 ，时， 1 0， 为无限小， T1 f t 由周期信号 非周期信号。 4

T1 2T1
T1 5E
Fn
2π
O 1 2 1


第一个零点集中了信号绝大部分能量（平均功率）
由频谱的收敛性可知，信号的功率集中在低频段。
X
第
周期矩形脉冲信号的功率
1 P T
16 页

T
0
f 2 ( t )dt
n


Fn
2

n


F ( n1 )
2
1 1 以 s, T1 s为例，取前5 次谐波 20 4
X
1 2 1


第
4．讨论
2π 谱 线 间 隔1 不变 T1不变， 改变 T1 E 2π 幅 度 , 第 一个 过零 点 T1
f (t ) E
12 页

方波信号的频谱方波信号的频谱是指方波信号在频率域内的分布情况。

方波是一种典型的非正弦波形，其频谱中具有一系列谐波分量，是由一系列正弦波组合而成的。

下面将从什么是方波信号、方波频谱的分布特点以及实际应用三个方面来介绍方波信号的频谱。

一、什么是方波信号方波信号是一种周期性矩形波，其波形由“高-低-高-低”等形态构成。

其数学表达式为：f(t)=A，0≤t≤T/2f(t)=-A,T/2≤t≤T其中A为幅值，T为周期，f(t)为在t时刻的幅值大小。

二、方波频谱的分布特点方波信号的频谱具有以下特点：1. 谐波分量丰富方波信号的频谱包含无限多个奇数谐波分量，即：f1=1/T、f3=3/T、f5=5/T、f7=7/T……2. 高频分量密集方波信号的频谱中，高频分量密集，而低频分量较少。

这是因为方波波形具有急剧变化的特点，必须包含相当多的高频成分才能还原出其原始波形。

3. 谐波幅值比例递减随着谐波频率的递增，其幅值比例也会递减。

这是由于方波信号的能量随着频率的递增而逐渐减小。

三、方波频谱的实际应用方波频谱具有广泛的应用领域，主要体现在以下方面：1. 信号合成方波信号的频谱可以通过合成一系列谐波信号来实现。

这些谐波信号可以分别调整其幅值、相位和频率，以实现各种需要的信号合成。

2. 信号分析方波信号的频谱可以用来分析信号的性质和特点。

通过分析方波波形的频谱分布，可以得知信号中包含了哪些谐波分量、它们的频率和幅值等信息，进而对信号进行分析和处理。

3. 音乐合成方波信号的频谱可以用来生成各种样式的音乐。

例如，将一组方波波形混合在一起，可以生成富有节奏感和节拍的音乐。

总之，方波信号的频谱是用来描述方波波形在频域内特征的工具。

通过对方波频谱的分析和合成，我们可以应用它在各个方面，如信号合成、信号分析和音乐合成等领域。

三、周期信号的频谱及其特点
3. 频谱的特性
(3) 信号的有效带宽
0~2 / 这段频率范围称为周期矩形脉冲信号的 有效频带宽度,即 2π B

信号的有效带宽与信号时域的持续时间成反比。 即 越大，其B越小；反之， 越小，其B 越大。
三、周期信号的频谱及其特点
3. 频谱的特性
(3) 信号的有效带宽 物理意义：在信号的有效带宽内，集中了信 号绝大部分谐波分量。若信号丢失有效带宽以 外的谐波成分，不会对信号产生明显影响。
n=—4 4
1 T /2 2 P T / 2 f (t )dt 0.2 T 包含在有效带宽(0 ~ 2 / )内的各谐波平均功率为
2 2 C0
2 | Cn | 2 0.1806
n=1
4
P 0.1806 1 90% P 0.200
例3 试求周期矩形脉冲信号在其有效带宽(0~2 /t)内
频谱的特性频谱的特性信号的有效带宽信号的有效带宽这段频率范围称为周期矩形脉冲信号的有效频带宽度有效频带宽度即信号的有效带宽与信号时域的持续时间信号的有效带宽与信号时域的持续时间成反比
连续周期信号的频域分析
周期信号的傅里叶级数展开 傅里叶级数的基本性质 周期信号的频谱及其特点 周期信号的功率谱
三、周期信号的频谱及其特点
三、周期信号的频谱及其特点
4. 相位谱的作用
幅频不变，零相位
幅频为常数，相位不变
四、周期信号的功率谱
帕什瓦尔(Parseval)功率守恒定理
2 1 T P 2T f (t ) dt Cn T 2 n 2
物理意义：任意周期信号的平均功率等于信号所 包含的直流、基波以及各次谐波的平均功率之和。

A、计算|Fn |和θn
4.3
周期信号的频谱及特点
2）、周期矩形脉冲的频谱
有一幅度为E，脉冲宽度为τ的周期矩 形脉冲，其周期为T，如图所示。求 频谱。 T τ
−
τ
2
τ
2
Fn =
1 T
∫
2
T − 2
f (t ) e
− jnΩt
E e− jnΩt = T − jnΩ
τ
2 −
τ
2
E 2 − jnΩt dt = dt τ e ∫ − T 2 nΩτ sin( ) Eτ sin nΩτ 2E 2 2 = = T nΩτ T nΩ
1）、定义
依据复傅立叶系数Fn随nΩ的变化关系所画的图称为 双边频谱图，简称双边谱； |Fn|~ nΩ为双边幅度谱，见图4.3-1（b）；其 以纵轴对称。 θn~ nΩ为双边相位谱。见图4.3-1（d）图。其 以原点对称。
第 第23 23-8 8页 页
■
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案 电子教案
, n = 0,1,2,..., φ0 = 0.
Fn ~ nΩ
θ n ~ nΩ
周期信号的频谱是指周期信号中各次谐波幅值、相位随 频率的变化关系。
第 第23 23-3 3页 页
■
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案 电子教案
4.3
A0 f (t ) = + 2
∞
周期信号的频谱及特点
ω1
T τ = = 2π Ω τ T
2π
见课本P131 页图4.3-4。
增多。
(b)、 τ 一定，T增大，谱线间隔 Ω 减小，频谱谱 线密度增大。谐波幅度减小：

X
第
1．三角形式的谱系数
f (t ) E
9 页
T1

f t 是个偶函数
bn 0, 只有a0 , an
O 2 2
T1
t
X
第
2．指数形式的谱系数
1 Fn T1
10 页

1 = T1
T1 2 T 1 2
f ( t )e jn1t d t

2
E 1 jn 1 t 2 Ee dt e jn1t 2 T1 jn 1
P5 n F 0 F 1 F 2 1 F 3 1 F 4 1
2 2 2 2
2
F 1 F 2 1 F 3 1 F 4 1
2 2 2
2
0.181E 2 1 T1 2 f ( t )dt 0.2 E 2 而总功率 T1 0 P5 n 二者比值 90.5% P
jn 1 jn1 2 e e 2

2
E jn 1T1


2E sin n 1 n 1T1 2 sin n 1 E 2 E Sa n 1 T1 T1 2 n 1
X
3．频谱及其特点

n)
E

f (t )
E 2E 1 f (t ) [sin(1 t ) sin(31 t ) 2 3 1 1 sin(51 t ) sin(n1 t ) ] 5 n

T1

T1 2
0
T1 2
T1
t
n 1,3,5,
E 2E 2E f (t ) cos(1 t ) cos(31 t ) 2 2 3 2 2E 2E cos(51 t ) cos(71 t ) 5 2 7 2

号的调制与解调等等。
精选版课件ppt
2
本章主要内容
3.1 3.2 3.3 3.4 3.5
周期信号的分解与合成 周期信号的频谱及特点 非周期信号的频谱 傅氏变换的性质与应用（1） 傅氏变换的性质与应用（2）
精选版课件ppt
3
本章主要内容
3.6 周期信号的频谱 3.7 系统的频域分析 3.8 无失真传输系统与理想低通滤波器 3.9 取样定理及其应用 3.10 频域分析用于通信系统
0 0 20 30 40 50
0.15
精选版课件ppt
14
周期信号的单边频谱
已知周期信号 f(t)11c o ts2 1s in t
2 4 3 4 3 6
求其基波周期T，基波角频率0，画出它的单边频谱图。
解：将f(t)改写为： f(t) 1 1 c o t s2 1 c o t s 2 4 3 4 3 62
精选版课件ppt
13
周期信号的单边频谱
画出周期信号 f(t) 的振幅频谱和相位频谱。
f(t) 1 si0 n t 2 co 0 t sco 20 ts ( 4 )
f(t) 1 5 co 0 ts 0 .( 1) 5 c o 20 s t 4
Ak 5
k
0.25
1
1
0
0
20 30 40 50
相位频谱图描述各次谐波的相位与频率的关系。
根据周期信号展开成傅里叶级数的不同形式，频谱图又分 为单边频谱图和双边频谱图。
精选版课件ppt
8
周期信号的单边频谱
周期信号 f ( t ) 的三角函数形式的傅里叶级数展开式为
f(t)A0 Ancos(n1tn) n1
A n 与 n 1 的关系称为单边幅度频谱；

实验四、周期信号的傅里叶级数和频谱分析1实验目的1）学会利用MATLAB 分析傅里叶级数展开，并理解傅里叶级数的物理含义； 2）学会利用MATLAB 分析周期信号的频谱特性。

2实验原理及实例分析2.1 周期信号的傅里叶级数（基本原理请参阅教材第四章的4.1节和4.2节。

）例1：周期方波信号)(t f 如图1所示，试求出该信号的傅里叶级数，利用MATLAB 编程实现其各次谐波的叠加，并验证Gibbs 现象。

f(t)t(sec)图1 周期方波信号)(t f 的波形图解：从理论分析可知，周期方波信号)(t f 的傅里叶级数展开式为)9sin 917sin 715sin 513sin 31(sin 4)(00000 +++++=t t t t t t f ωωωωωπ其中，ππω220==T。

则可分别求出1、3、5、9、19、39、79、159项傅里叶级数求和的结果，其MATLAB 程序如下，产生的图形如图2所示。

close all;clear all; clct = -2:0.0001:2; omega = 2 * pi;y = square(2 * pi * t,50); n_max = [1 3 5 9 19 39 79 159]; N = length(n_max); for k = 1:Nfk = zeros(1,length(t)); for n = 1:2:n_max(k) bn = 4 / (pi * n);fk = fk + bn * sin(n * omega * t); endfigure; plot(t,y,t,fk,'Linewidth',2); xlabel('t(sec)');ylabel('部分和的波形'); String = ['最大谐波数=',num2str(n_max(k))];axis([-2 2 -3 3]);grid; title(String);disp([String,'时，在信号跳变点附近的过冲幅度（%）']);f_max = (max(fk) - max(y)) / (max(y) - min(y)) * 100 endt(sec)部分和的波形最大谐波数=1t(sec)部分和的波形最大谐波数=3t(sec)部分和的波形最大谐波数=5t(sec)部分和的波形最大谐波数=9t(sec)部分和的波形最大谐波数=19t(sec)部分和的波形最大谐波数=39t(sec)部分和的波形最大谐波数=79t(sec)部分和的波形最大谐波数=159图2 例1程序产生的图形程序输出的用于验证Gibbs 现象的数值分别为：13.6620 10.0211 9.4178 9.1164 8.9907 8.9594 8.9484 8.94642.2周期信号的频谱分析（基本原理请参阅教材第四章的4.3节。

0
2
T
t
谱线间隔不变 2
T
Fn
1 8
2
0
第一个过零点增加一倍
幅值减小一倍
-
3
周期T不变，脉冲宽度变化 ③
情况 3： 1 T,6 F nT S(n a T ) 1 1S 6(n 1 a )6 ， 第一个过零点为 n =16 。
脉冲宽度再缩小一倍
f (t)
T
1
2
0
2
T
t
谱线间隔不变 2
周期矩形脉冲的频谱
f (t)
1
T
2
0
2
T
t
F n T 1 2 2e j n td T 1 t e j j n t n 2 2 T 2 s n n i 2 n T s n 2 n i 2 nn 0 , 1 , 2 ,
令 Sa(x) sinx 称为抽样函数，为偶函数。当 x0时 Sa(0)1，
f (t)
T
谱线间隔 2
T
1
2
0
2
1 Fn
4
T
t
第一个过零点：
S
a(2)0
2
2 4
2
0
Fn 在n有值，称为谱线；
-
2
周期T不变，脉冲宽度变化 ②
情况 2：T 8,F nT S(n a T )8 1S(n a 8 )， 第一个过零点为 n =8 。
脉冲宽度缩小一倍
f (t)
1
T
2
1 4
FFnn
1
8
幅值减小一倍
0
22
第一个过零点不变
-
7
脉冲宽度不变, 周期T变化 ③
情况 3：T16时，谱线间隔 2 ， 第一个过零点 2 。

X (k ) RMS =
Im(k ) , 函数 Complex To Polar 可直接得 2* Re 2 (k ) + Im 2 (k ) ，相位谱为 ϕ (k ) = arctan Re(k ) 2
到复数的模和相位角。 再把用弧度表示的相位转换为角度。 使用两个图形控件显示幅度谱和 相位谱。 程序面板如下图所示：
五、实验步骤：
1．设计 DFT 变换程序，求取仿真信号的幅值频谱和相位谱。 （要求仅采用基本数学 函数实现） 。 分析：DFT 计算公式为： X (k ) = ∑ x(n)e
n =0 N −1 −j 2π nk N
其中
k = 0,1,2..., N − 1 ，采用双循环， n = 0,1,2..., N − 1
先固定 k，内循环累加求和，计算 ∑ x(n)e
n =0
N −1
−j
2π nk N
，再改变 k，外循环。最后将 X(k)转换为幅
度谱和相位谱。设计中要用到数值运算子模板中的 Complex Functions 复数处理函数。 （1）产生仿真信号。打开 3.5 节第 2 个实验内容的程序，它能够产生频率、幅值和 直流偏值可调的正弦、方波、三角波、锯齿波信号，还可叠加高斯噪声信号，并且采样率和 采样点可选。 （2）计算 = n 0,1, 2..., N − 1 ，结果为 1 个数组，见图
2) 3) 4)
各节点之间的频率间隔由时间长度 N 和采样频率 fs 决定： 第 k 个节点对应的频率值为 有一半数据有意义。
f (k ) = k ⋅ fs N 。
FFT形成的频谱相对于折叠频率f S /2 对称，FFT的输出频率范围为 0～f S /2。实际只
用 DFT 进行测试信号频域特性分析存在主要误差有量化误差、混叠误差、频谱泄漏和 栅栏效应等，减少计算误差的办法有，增加 A/D 的有效位数，提高采样频率，增加采样时 间和采样点数，整周期采样或加窗处理等。

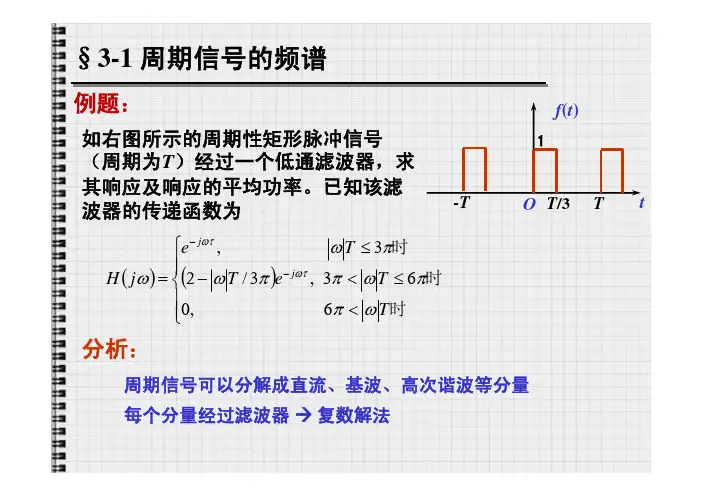
例题：O tf (t )T /31-TT如右图所示的周期性矩形脉冲信号（周期为T ）经过一个低通滤波器，求其响应及响应的平均功率。

已知该滤波器的传递函数为()()⎪⎪⎩⎪⎪⎨⎧<≤<-≤=--时时时T T e T T e j H j j ωππωππωπωωωτωτ6,063,3/23,分析：周期信号可以分解成直流、基波、高次谐波等分量每个分量经过滤波器 复数解法解：求傅立叶系数：⎰-=3/001T tjn n dt eTC ωO tf (t )T /31-TT令ω0=2π/T3/0001T t jn eTjn ωω--=3/3sin 31ππjn e n c -⎪⎭⎫ ⎝⎛=3100==C A 2nj n n A eC ϕ=~基波和n 次谐波的复数表示低通滤波器只通过低于3ω0的信号，因此信号中只有直流、基波和二次谐波分量通过。

输出信号中的直流分量为：()3100==ωωj H A解：输出信号中的基波分量的复数表示为：()()τωπωωφπω0013/13sin 32+-=⎪⎭⎫ ⎝⎛=j j e c j H eA 输出信号中的二次谐波分量的复数表示为：()()τωπωωφπω00223/22232sin 94+-=⎪⎭⎫⎝⎛=j j e c j H e A 输出信号的时域表达式为：⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛+τωπωπτωπωπ00002322cos 32sin 943cos 3sin 3231t c t c 输出信号的平均功率为：280.02sin 41sin 211222≈⎥⎤⎢⎡⎪⎫⎛+⎥⎤⎢⎡⎪⎫ ⎛+⎪⎫ ⎛=ππc c P out第三章：信号的频谱§3-1 周期信号的频谱§3-2 非周期信号的频谱密度 傅立叶变换与频谱密度信号的频谱分布与带宽基本信号的频谱密度§3-3 频谱分析的基本定理§3-4 采样定理傅立叶变换的引出如何从频域描述一个非周期信号？tf (t )傅立叶级数？——显然不行怎么办？退而求其次，先考虑描述函数在有限区间[a,b)上的一段吧tf a,b (t )a btf T (t )a b考虑有限区间周期扩展再扩展成周期T =b -a 的函数f T (t )f T (t ):周期函数~可以用傅立叶级数表示在区间[a,b)上与f (t ) 相同傅立叶变换的引出tf T (t )a b()(),1100dt et f Tdte tf T C tjn bat jn ba T n ωω--⎰⎰==()()()⎪⎪⎩⎪⎪⎨⎧=-++∈-++=∑∞-∞=b a t b f a f b a t t f t f eC n tjn n或,2)0(0,,2)0(00ω傅立叶级数只在区间(a,b ) 上收敛于f (t )，因此C n 并不是f (t ) 的复频谱如果f T (t ) 满足狄利克雷条件，则可以展开成傅立叶级数：定义：则：ω0=2π/T傅立叶变换的引出进一步，选取对称区间[-T /2,T /2)。

矩形窗函数的频谱矩形窗函数是一种常见的信号处理工具，用于对信号进行调节和滤波。

在频率分析中，矩形窗函数也被广泛应用，能够帮助我们理解信号的频域特性。

本文将介绍矩形窗函数如何影响信号的频谱，并提出一些应用实例和注意事项。

一、矩形窗函数的定义和特性矩形窗函数是一种基本的周期性函数，形如：w(n) = 1，当0 <= n <= N-1；w(n) = 0，其它情况。

其中N表示窗函数的长度，n为序号。

矩形窗函数还有一些重要的特性：1. 窗函数在频域中的傅里叶变换是正弦函数。

2. 矩形窗函数在时域中具有周期性。

3. 矩形窗函数的瞬时能量和平均功率相等。

二、矩形窗函数的频谱分析矩形窗函数的频谱分析是通过傅里叶变换将其转换到频域中进行的。

根据矩形窗函数的定义和特性，我们可以得到其傅里叶变换的表达式：W(f) = (1/N) * sin(N * pi * f) / sin(pi * f)其中f为频率。

这个式子可以帮助我们理解矩形窗函数对信号频谱的影响。

首先，可以发现矩形窗函数的频谱是以周期为N的正弦曲线波动的。

这是因为窗函数在时域中具有周期性，在频域中表现出正弦曲线的形式。

其次，可以发现当f=0时，傅里叶变换的结果为N。

这意味着矩形窗函数对低频信号的增益是N，也就是它本身的长度。

当f=1/2时，傅里叶变换的结果为0，这意味着矩形窗函数对高频信号的抑制作用最强，实际上它完全挡住了所有高频信号。

因此，矩形窗函数通常会对低频信号的增益和高频信号的抑制造成一定的影响。

三、矩形窗函数的应用实例矩形窗函数在实际应用中有很多用途，以下是一些例子：1. 在傅里叶变换中使用矩形窗函数可以将信号的频谱沿着一定的间隔切割成不同的段落。

这可以有助于对信号的频域特征进行更细致和深入的分析。

2. 在数字信号处理中，矩形窗函数经常用作数据处理窗口，来调整信号的周期性和平滑性。

3. 在基于傅里叶变换的频率分析方法中，矩形窗函数经常用作平滑滤波器，以消除噪声和假信噪比等问题。

4
狄利克雷（Dirichlet）条件 条件1：在一周期内，如果有间断点存在，则间断点的 数目应是有限个。
条件2：在一周期内，极大值和极小值的数目应是有 限个；
条件3:在一周期内，信号绝对可积;
5
狄利克雷（Dirichlet）条件1:例1 不满足条件1的例子如下图所示，这个信号的周期 为8，它是这样组成的：后一个阶梯的高度和宽度是前一 个阶梯的一半。可见在一个周期内它的面积不会超过8， 但不连续点的数目是无穷多个。
0
1
1
0
1
2 1
2 1
指数形式的频谱图
F n 1
0.15
n
0.5
1.12
1
1.12
0.5
2 1
0.15 2 1
1
0.25
2 1 1
0
1
1
0
0.15
2 1
0.25
21
四．总结
（1）周期信号f(t)的傅里叶级数有两种形式

满足离散性，谐波性不满足收敛性，频带无限宽
26
一．频谱结构
f (t ) E
/ 2
脉宽为 脉冲高度为E 周期为T1
T1
/2
T1
t
1. 指数函数形式的谱系数
2. 频谱特点
27
1．指数形式的谱系数
1 F ( n 1 ) T1
1 = T1
jn 1 t

T1
T1
2 2
f ( t )e jn1t d t
bn n tg a n
1
关于的偶函数（实际 n 取正值） 关于的奇函数（实际 n 取正值） 关于的偶函数 关于 的奇函数

4.3周期信号的频谱
一、频谱的概念
广义上，信号某些特征量随信号频率变化的关系称信号频谱
画出的图形称为信号的频谱图。 周期信号的频谱即周期信号的各次谐波幅值，相位随频率的变 化关系。
频谱的分类
幅度频谱:以角频率 （或角频率 ）为横坐标，以 An / Fn 为 纵坐标 相位频谱：以频率 （或角频率 ）为横坐标，以 n 为纵 坐标 （A0为直流分量幅度；An为n次谐波的振幅； n 为n次谐波 的初相角）
A0 2 1 2 1 A0 2 2 T [( ) T 0 A n ] ( ) A n T 2 2 2 n 1 n 1 2
周期信号的功率等于直流分量的功率和各次谐波的功 率之和。 1 | Fn | An 2
1 P T
n

T 2 T 2
谐波性
频谱的每条谱线只能出现在基波频率的整数倍频率上。
结论
周期信号的频谱特点：
（1）离散性
（2）谐波性 （3）收敛性
信号的有效带宽
0~2 / 这段频率范围称为周期矩形脉冲信号的有效频带宽 度,即第一个零点以内的这段频率范围称为信号的频带宽度或 者信号的带宽。
B
2π

结论：矩形脉冲的频带宽度与脉冲宽度成反比。 即 越大，其wB越小；反之， 越小，其wB 越大。 物理意义：在信号的有效带宽内，集中了信号绝大部 分谐波分量。若信号丢失有效带宽以外的谐波成分，不 会对信号产生明显影响。
（3）频谱结构与波形参数的关系（T1, ）
（1）设f(t)中的 E不变，不变， 当周期1变化时，频谱如何变化？
(1)


1 s 20
1 s 20
T1
T1

周期信号的频谱的特点一、 周期信号的频谱一个周期信号)(t f ，只要满足狄里赫利条件，则可分解为一系列谐波分量之和。

其各次谐波分量可以是正弦函数或余弦函数，也可以是指数函数。

不同的周期信号，其展开式组成情况也不尽相同。

在实际工作中，为了表征不同信号的谐波组成情况，时常画出周期信号各次谐波的分布图形，这种图形称为信号的频谱，它是信号频域表示的一种方式。

描述各次谐波振幅与频率关系的图形称为振幅频谱，描述各次谐波相位与频率关系的图形称为相位频谱。

根据周期信号展成傅里叶级数的不同形式又分为单边频谱和双边频谱。

1单边频谱若周期信号)(t f 的傅里叶级数展开式为式(3-15)，即∑ ∞=+Ω+=10)cos()(n n n t n A A t f ϕ (3-24)则对应的振幅频谱n A 和相位频谱n ϕ称为单边频谱。

例3-3 求图3-4所示周期矩形信号)(t f 的单边频谱图。

解 由)(t f 波形可知， )(t f 为偶函数，其傅里叶系数⎰==2/0021)(4T dt t f T a⎰=Ω=2/0)4/sin(2cos )(4T n n n tdt n t f T a ππ0=n b故∑∑∞=∞=Ω+=Ω+=110cos )4/sin(241cos 2)(n n n tn n n t n a a t f ππ因此410=A , ππn n A n)4/sin(2=即45.01=A , 32.02≈A , 15.03≈A , 04=A , 09.05≈A , 106.06≈A ┅单边振幅频谱如图3-5所示。

tf(t)图 3 - 4ττττ4 2/ 0 2/ 4--1图 3 - 50.250.450.320.150.090.106ΩΩΩΩΩΩΩ7 6 5 4 3 2 0A n2双边频谱若周期信号)(t f 的傅里叶级数展开式为式(3-17)，即25)-(3 )(∑∞-∞=Ω=n tjn neF t f则n F 与Ωn 所描述的振幅频谱以及n F 的相位n n F θ=arctan 与Ωn 所描述的相位频谱称为双边频谱。

周期矩形脉冲信号的分析
假设周期矩形脉冲信号f(t)的脉冲宽度为τ，脉冲幅度为E,重复周期为T，如以下图所示
这种信号的表示为
1.求f(t)的复数振幅和展开成傅里叶级数
此等式是三角傅里叶级数展开式，由此作出单边谱。

上式为指数傅里叶展开式，由此画出双边谱。

2.画频谱图
由复振幅的表达式可知，频谱谱线极点的联线所组成的包络是抽样函数。

1)找出谐波次数为零的点（即包络与横轴的交点）
包络线方程为,与横轴的交点由下式决定：
假设这些频率恰好基波频率恰好是基波频率的整数倍，那么相应的谐波为零。

因此，包络线与横轴的交点应知足两个条件：一是谐波条件；二是谐波为零的条件。

2)粗略求出各次谐波的振幅值
由的表达式可知,当时，最大值为，即当时，第一个零点内含有二条谱线，依次类推，就大致画出了振幅频谱图。

3）相位的确信
将代入可知，，当角度在第一、二象限时为正实数，即相位为零；当角度在第三、四象限时为负实数，即相位为π。

3.频谱特点分析
1)频谱是离散的,两谱线间的距离为基波频率,脉冲周期越大，谱线越密。

2)由知：各分量的大小与脉幅成正比，与脉宽成正比，与周期成反比。

当E变大时,τ变大，那么各次谐波的幅度愈大；T变大,那么谐波幅度愈小。

3)各谱线的幅度按包络线转变,当时，谱线的包络通过零值。

4)主要能量在第一过零点内。

主带宽度为：。

1、周期信号的频谱周期信号在满足一定条件时,可以分解为无数三角信号或指数之与。

这就就是周期信号的傅里叶级数展开。

在三角形式傅里叶级数中,各谐波分量的形式为()1cos n n A n t ωϕ+;在指数形式傅里叶级数中,分量的形式必定为1j n tn F eω 与1-j -n tn F eω 成对出现。

为了把周期信号所具有的各次谐波分量以及各谐波分量的特征(如模、相角等)形象地表示出来,通常直接画出各次谐波的组成情况,因而它属于信号的频域描述。

以周期矩形脉冲信号为lifenxi 周期信号频谱的特点。

周期矩形信号在一个周期(-T/2,T/2)内的时域表达式为,20,>2()A t T t f t ττ≤⎧=⎨⎩(2-6)其傅里叶复数系数为12n n A F Sa T ωττ⎛⎫=⎪⎝⎭(2-7) 由于傅里叶复系数为实数,因而各谐波分量的相位为零(n F 为正)或为π±(n F 为负),因此不需要分别画出幅度频谱n F 与相位频谱n φ。

可以直接画出傅里叶系数n F 的分布图。

如图2、4、1所示。

该图显示了周期性矩形脉冲信号()T f t 频谱的一些性质,实际上那个也就是周期性信号频谱的普遍特性: ① 离散状频谱。

即谱线只画出现在1ω的整数倍频率上,两条谱线的间隔为1ω(等于2π/t)。

② 谱线宽度的包络线按采样函数()1/2a S n ωτ的规律变化。

如图2、4、2所示。

但1ω为2πτ时,即()2m πωτ=(m=1,2,……)时,包络线经过零点。

在两相邻 零点之间,包络线有极值点,极值的大小分别为-0、212()2A T τ,0、127()2A T τ,……③谱线幅度变化趋势呈收敛状,它的主要能量集中在第一个零点以内,因而把w=0- 2 / 这段频率范围称为信号的有效带宽, B ω或B f2B rad πωτ=1B f hz τ=图2、4、12、4、2 频谱包络线由上两式可见,信号频带宽度只与脉宽 有关,且成反比关系,这时信号分析中最基本的特性。