离散数学课件16.3根树及其应用
- 格式:ppt
- 大小:248.50 KB
- 文档页数:32

离散数学是数学的一个分支,主要研究离散对象的性质和关系。
在离散数学中,树和图是两个重要的概念和工具。
它们不仅在数学中具有重要的地位,而且在计算机科学、电子工程、通信工程等领域中也有广泛的应用。
首先,让我们来了解一下树和图的定义。
在离散数学中,树是一种特殊的图。
树是由若干个节点组成的,其中一个节点被称为根节点,其他节点分布在根节点之下的若干层次中,并且每个节点最多有一个父节点。
除此之外,树的每个节点可以有零个或多个子节点。
树的一个重要特点是:任意两个节点之间有且仅有一条路径相连。
在离散数学中,图是由若干个节点和连接节点的边组成的。
图可以分为有向图和无向图。
有向图中的边是有方向的,无向图中的边没有方向。
图的节点可以表示实体,边可以表示实体之间的关系。
图的一个重要特点是:图中的节点和边可以有多个连接。
树和图有着广泛的应用。
在计算机科学中,树和图常常被用于数据结构和算法。
比如,树可以用来实现二叉搜索树、堆、二叉树等数据结构;图可以用来实现图算法,如最短路径算法、最小生成树算法、拓扑排序算法等。
树和图的应用还涉及到网络优化、模式识别、数据挖掘、人工智能等领域。
在电子工程中,树和图被用来描述和分析电路。
树可以用来表示电路的拓扑结构,图可以用来表示电路元件之间的连接关系。
树和图在电路分析和设计中起到了至关重要的作用。
比如,树可以用来分析电路的戴维南等效电路、回路等;图可以用来优化电路的布局和布线。
在通信工程中,树和图被用来表示通信网络和通信路径。
通信网络可以看作是由节点和连接节点的通信链路组成的图,而通信路径可以看作是图中的一条路径。
树和图在通信网络的规划、管理和优化中扮演重要的角色。
比如,树可以用来构建网络拓扑,图可以用来分析和优化通信路径。
总之,离散数学中的树和图是非常重要的概念和工具,并且在各个领域中有广泛的应用。
无论是计算机科学、电子工程还是通信工程,都离不开树和图的帮助。
因此,我们应该加强对树和图的学习和应用,以更好地解决实际问题。

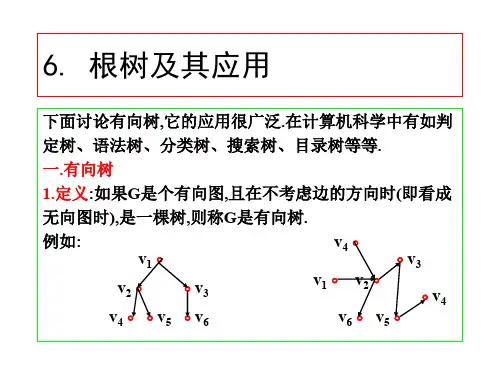






离散数学及应用课件离散数学是数学的一个重要分支,它研究的是数学离散对象,如集合、图、树、数等。
它涵盖了一系列丰富而又有深度的主题,包括集合论、图论、数论、逻辑学等。
这些主题不仅在数学领域有着广泛的应用,也在计算机科学、物理学、经济学等多个领域有所涉及。
一、离散数学的主要内容1、集合论:集合论是离散数学的基础,它研究的是集合及其性质和运算。
集合论中的基本概念包括元素、集合、子集、并集、交集、补集等。
2、图论:图论是离散数学中一门研究图形和网络结构的学科。
图论中的基本概念包括节点、边、路径、环、子图等。
图论在计算机科学、电子工程、交通运输等领域都有广泛的应用。
3、数论:数论是研究整数性质和运算的学科。
数论中的基本概念包括整数、素数、合数、约数、倍数等。
数论在密码学、计算机科学等领域有着重要的应用。
4、逻辑学:逻辑学是研究推理和证明的学科。
逻辑学中的基本概念包括命题、推理、证明、反证等。
逻辑学在人工智能、哲学、法学等领域有着广泛的应用。
二、离散数学的应用1、计算机科学:离散数学在计算机科学中的应用广泛而重要。
例如,图论被用于解决计算机科学中的一些基本问题,如排序问题、旅行商问题等。
离散数学还在计算机科学的其他领域有所应用,如算法设计、数据结构、数据库系统等。
2、物理学:离散数学在物理学中的应用也十分广泛。
例如,量子力学和统计力学的理论框架中都有离散数学的影子。
离散数学还在固体物理学、分子物理学等领域有所应用。
3、经济学:离散数学在经济学中的应用也日益增多。
例如,离散数学被用于研究金融市场中的复杂行为,以及分析经济数据的模式和趋势。
离散数学还在博弈论、决策理论等领域有所应用。
三、总结离散数学作为数学的一个重要分支,其理论和应用已经渗透到科学的各个领域。
学习和研究离散数学,不仅可以增强我们的数学素养,还可以提高我们的逻辑思维能力和解决问题的能力。
因此,我们应该重视离散数学的学习和应用。
离散数学是数学的一个重要分支,它研究的是离散量的结构及其相互关系。

离散数学是数学的一个分支,与连续数学相对应,主要研究离散对象和离散结构。
在离散数学中,树是一种重要的数据结构,它不仅在数学中有着广泛的应用,而且在计算机科学、图论等领域也起到了重要的作用。
首先,我们来了解一下什么是树。
在离散数学中,树是一种无环连通图,它是由若干个节点(或称为顶点)和这些节点之间的边组成。
树有一个特殊的节点,称为树根,它是树中唯一的一个节点,其他节点都可以通过一条边从根节点到达。
树中的节点按照层次关系分为不同的层次,根节点位于第一层,每一个节点的子节点位于它的下一层。
树还可以为空,即不包含任何节点。
树作为一种数据结构,广泛应用于计算机科学中。
一个典型的应用就是构建文件系统。
我们知道,计算机中的文件可以以树的结构进行组织,根目录是树的根节点,每一个文件夹是树的一个节点,文件夹中的文件是该节点的子节点。
通过树的结构,我们可以很方便地查找和管理文件。
另一个重要的应用是在数据库中的索引结构中。
数据库中的索引可以理解为一个树形结构,每一个节点存储了数据的关键字和相应的记录指针。
通过索引树,我们可以快速地查找到数据库中的数据,提高了数据库的查询效率。
此外,在图论中,树也是一个重要的概念。
图论研究的是图的性质和图中的关系,而树是一种特殊的图。
树的概念在图论中被广泛应用,比如最小生成树算法、最短路径算法等。
此外,在离散数学中,树的应用还有很多。
比如在数学中,树的概念可以帮助我们解决一些排列组合、概率等问题。
在逻辑学中,树还可以用来表示一个命题的逻辑结构,帮助我们分析和推理。
总而言之,离散数学中的树是一种重要的数据结构,它不仅在数学中有着广泛的应用,而且在计算机科学、图论等领域也起到了重要的作用。
通过树的结构,我们可以更加高效地组织数据,快速地搜索和查找信息。
树的概念也可以帮助我们解决一些数学和逻辑问题。
因此,掌握离散数学中的树的概念和应用,对于我们理解和应用离散数学领域的知识,具有重要的意义。
