哈夫曼树及其应用(完美版)

哈夫曼编码树实现及应用场景讲解哈夫曼编码树（Huffman coding tree）是一种被广泛应用于数据压缩的算法，它通过利用输出频率不同的字符分配不同长度的编码，从而实现数据的高效压缩。

本文将介绍哈夫曼编码树的实现方法，并探讨其在实际应用中的场景。

一、哈夫曼编码树的实现方法1.1 字符频率统计在构建哈夫曼编码树之前，我们首先需要对目标数据中的字符进行频率统计。

可以通过遍历数据集，并利用哈希表或数组记录每个字符出现的次数。

例如，对于字符串"Hello World!"，我们可以统计出每个字符的频率为：H: 1, e: 1, l: 3, o: 2, W: 1, r: 1, d: 1, !: 1。

1.2 构建哈夫曼编码树构建哈夫曼编码树的过程分为两个步骤：创建叶节点集合和合并节点。

创建叶节点集合：根据字符频率统计结果，创建一个包含所有字符的叶节点集合。

每个叶节点包含字符、频率以及指向其左右子节点的指针（若存在子节点）。

合并节点：从叶节点集合中选取频率最低的两个节点，合并成一个新节点，该新节点的频率等于这两个节点的频率之和。

将合并后的节点插入叶节点集合中，并从集合中移除被合并的节点。

重复该操作，直到叶节点集合只剩下一个节点，即为哈夫曼编码树的根节点。

1.3 构建哈夫曼编码表遍历哈夫曼编码树，沿着根节点到叶节点的路径，给每个字符赋予对应的二进制编码。

例如，对于字符串"Hello World!"，哈夫曼编码表如下：H: 00e: 01l: 10o: 11W: 010r: 011d: 100!: 101二、哈夫曼编码树的应用场景2.1 数据压缩哈夫曼编码树最常见的应用场景之一是数据压缩。

通过使用较短的二进制编码表示频率较高的字符，以及使用较长的二进制编码表示频率较低的字符，可以大幅减小数据的存储空间。

这种压缩方法被广泛应用于文本、图像和音频等多媒体数据的传输和存储。

举个例子，在一个文件中，字符'E'出现频率最高，通过哈夫曼编码树，我们可以将其编码为一个比特（如0），而字符'Z'出现频率最低，可以将其编码为多个比特（如11001），从而实现数据的高效压缩。

哈夫曼树及其应用一、基本术语1．路径和路径长度在一棵树中，从一个结点往下可以达到的孩子或子孙结点之间的通路，称为路径。

通路中分支的数目称为路径长度。

若规定根结点的层数为1，则从根结点到第L层结点的路径长度为L-1。

2．结点的权及带权路径长度若将树中结点赋给一个有着某种含义的数值，则这个数值称为该结点的权。

结点的带权路径长度为：从根结点到该结点之间的路径长度与该结点的权的乘积。

3．树的带权路径长度树的带权路径长度(Weighted Path Length of Tree)：也称为树的代价，定义为树中所有叶结点的带权路径长度之和，通常记为：其中：n表示叶子结点的数目wi和li分别表示叶结点ki的权值和根到结点ki之间的路径长度。

二、哈夫曼树构造1．哈夫曼树的定义在权为w l，w2，…，w n的n个叶子所构成的所有二叉树中，带权路径长度最小(即代价最小)的二叉树称为最优二叉树或哈夫曼树。

【例】给定4个叶子结点a，b，c和d，分别带权7，5，2和4。

构造如下图所示的三棵二叉树(还有许多棵)，它们的带权路径长度分别为：(a)WPL=7*2+5*2+2*2+4*2=36(b)WPL=7*3+5*3+2*1+4*2=46(c)WPL=7*1+5*2+2*3+4*3=35其中(c)树的WPL最小，可以验证，它就是哈夫曼树。

2．哈夫曼树的构造假设有n个权值，则构造出的哈夫曼树有n个叶子结点。

n 个权值分别设为w1,w2,…,wn,则哈夫曼树的构造规则为：(1) 将w1,w2,…,wn看成是有n 棵树的森林(每棵树仅有一个结点)；(2) 在森林中选出两个根结点的权值最小的树合并，作为一棵新树的左、右子树，且新树的根结点权值为其左、右子树根结点权值之和；(3)从森林中删除选取的两棵树，并将新树加入森林；(4)重复(2)、(3)步，直到森林中只剩一棵树为止，该树即为我们所求得的哈夫曼树。

下面给出哈夫曼树的构造过程，假设给定的叶子结点的权分别为1,5,7,3，则构造哈夫曼树过程如下图所示。

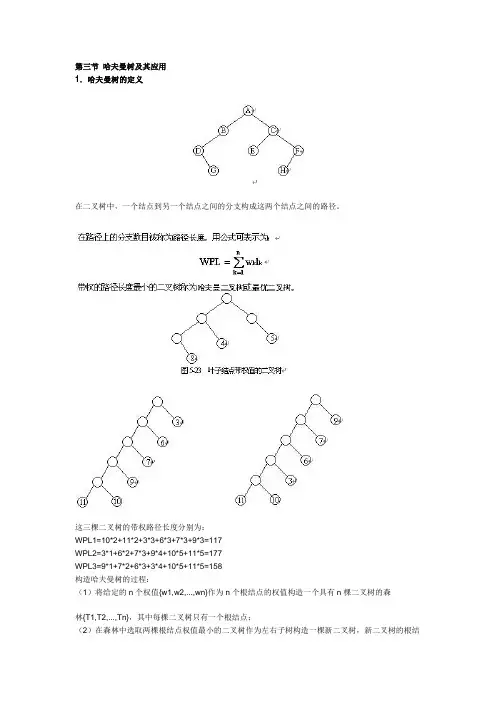
第三节哈夫曼树及其应用1．哈夫曼树的定义在二叉树中，一个结点到另一个结点之间的分支构成这两个结点之间的路径。

这三棵二叉树的带权路径长度分别为：WPL1=10*2+11*2+3*3+6*3+7*3+9*3=117WPL2=3*1+6*2+7*3+9*4+10*5+11*5=177WPL3=9*1+7*2+6*3+3*4+10*5+11*5=158构造哈夫曼树的过程：（1）将给定的n个权值{w1,w2,...,wn}作为n个根结点的权值构造一个具有n棵二叉树的森林{T1,T2,...,Tn}，其中每棵二叉树只有一个根结点；（2）在森林中选取两棵根结点权值最小的二叉树作为左右子树构造一棵新二叉树，新二叉树的根结点权值为这两棵树根的权值之和；（3）在森林中，将上面选择的这两棵根权值最小的二叉树从森林中删除，并将刚刚新构造的二叉树加入到森林中；（4）重复上面（2）和（3），直到森林中只有一棵二叉树为止。

这棵二叉树就是哈夫曼树。

假设有一组权值{5,29,7,8,14,23,3,11}，下面我们将利用这组权值演示构造哈夫曼树的过程。

这就是以上述8个权值为叶子结点权值构成的哈夫曼树，它的带权的路径长度为：WPL=(23+29)*2+(11+14)*3+(3+5+7+8)*4=2712．判定树在很多问题的处理过程中，需要进行大量的条件判断，这些判断结构的设计直接影响着程序的执行效率。

例如，编制一个程序，将百分制转换成五个等级输出。

大家可能认为这个程序很简单，并且很快就可以用下列形式编写出来：if (socre<60) printf("bad");else if (socre<70) printf("pass");else if (score<80) printf("general");else if (score<90) printf("good");esle printf("very good");在实际应用中，往往各个分数段的分布并不是均匀的。

哈夫曼树的实际应用
哈夫曼树（Huffman Tree）是一种重要的数据结构，它在信息编码和压缩、数据传输和存储、图像处理等领域有广泛应用。

1. 数据压缩：哈夫曼树是一种无损压缩的方法，能够有效地减小数据的存储空间。

在进行数据压缩时，可以使用哈夫曼树构建字符编码表，将出现频率较高的字符用较短的编码表示，而出现频率较低的字符用较长的编码表示，从而减小数据的存储空间。

2. 文件压缩：在文件压缩领域，哈夫曼树被广泛应用于压缩算法中。

通过构建哈夫曼树，可以根据字符出现的频率来生成不同长度的编码，从而减小文件的大小。

常见的文件压缩格式如ZIP、GZIP等都使用了哈夫曼树。

3. 图像压缩：在图像处理中，哈夫曼树被用于图像压缩算法中。

通过将图像中的像素值映射为不同长度的编码，可以减小图像的存储空间，提高图像传输和存储的效率。

常见的图像压缩格式如JPEG、PNG等都使用了哈夫曼树。

4. 文件传输：在数据传输中，哈夫曼树被用于数据压缩和传输。

通过对数据进行压缩，可以减小数据的传输时间和带宽占用。

在传输过程中，接收方可以通过哈夫曼树解码接收到的数据。

5. 数据加密：在数据加密中，哈夫曼树可以用于生成密钥，从而实现数据的加密和解密。

通过将字符映射为不同长度的编码，可以实
现对数据的加密和解密操作。

哈夫曼树在信息编码和压缩、数据传输和存储、图像处理等领域有广泛应用，能够有效地减小数据的存储空间、提高数据传输效率、实现数据加密等功能。

赫夫曼树的作用及应用1.引言在计算机科学中，赫夫曼树是一种重要的数据结构，它被广泛应用于数据压缩、存储和解码等领域。

赫夫曼树以其高效的特点，成为了压缩算法中的重要组成部分。

本文将介绍赫夫曼树的作用以及它在不同应用领域中的具体应用。

2.赫夫曼树的基本概念赫夫曼树，也称为最优二叉树，是一种树形结构。

它的构建基于赫夫曼编码算法，该算法通过将频率较高的字符编码为较短的二进制码，从而实现数据的高效压缩。

3.赫夫曼树的构建赫夫曼树的构建过程包括以下几个步骤：1.统计字符频率：遍历待压缩的数据，统计各个字符出现的频率。

2.构建叶子节点：将每个字符及其频率作为叶子节点，构成初始的二叉树。

3.合并节点：选择两个频率最低的节点合并，并将合并后的节点作为新的节点插入二叉树中。

4.重复合并：重复执行合并节点的操作，直到只剩下一个节点，即赫夫曼树的根节点。

4.赫夫曼树的作用赫夫曼树在数据压缩和解压缩中发挥着重要作用，主要体现在以下几个方面：4.1数据压缩赫夫曼树通过赫夫曼编码将频率较高的字符编码为较短的二进制码，从而实现数据的高效压缩。

压缩后的数据体积大大减小，方便存储和传输。

4.2文件压缩赫夫曼树可用于对文件进行压缩，将文件中的字符编码为对应的二进制码，从而减小文件的大小。

在文件传输和存储中，减小文件的大小可以提高传输速度和节省存储空间。

4.3图像压缩赫夫曼树也可用于图像数据的压缩，通过对图像中的像素进行编码，减小图像的大小。

图像压缩在图像处理和存储中起到重要的作用，减小图像的大小可以提高图像的传输速度和存储效率。

4.4视频压缩赫夫曼树在视频编码中也有重要应用，通过对视频帧中的数据进行编码，实现对视频的压缩。

视频压缩可以降低视频的带宽占用率，提高视频传输的效率和稳定性。

5.赫夫曼树的应用举例除了数据压缩方面，赫夫曼树在其他领域也有广泛应用，以下列举几个常见的应用场景：5.1字符串匹配赫夫曼树可以用于字符串匹配算法中，通过构建赫夫曼树和相关数据结构，提高字符串匹配的效率和准确性。

哈夫曼树除哈夫曼编码之外的应用
除了用于哈夫曼编码外，哈夫曼树还有一些其他的应用，包括：
1. 数据压缩：哈夫曼树被广泛应用于数据压缩算法中，如在文件压缩中常用的Huffman压缩算法。

该算法利用哈夫曼树将
频率较高的字符编码为较短的比特序列，从而实现数据的有效压缩。

2. 图像压缩：哈夫曼树可以用于图像压缩算法中的灰度压缩。

通过统计每个灰度级出现的频率，构建哈夫曼树，并将灰度级映射成相应的哈夫曼编码，实现图像数据的压缩。

3. 加密算法：哈夫曼树可以用于加密算法中，比如基于哈夫曼树的可逆数据隐藏算法。

该算法利用哈夫曼树将目标数据隐藏到另一段数据中，通过哈夫曼编码实现隐藏过程，解密时再利用哈夫曼树将隐藏的数据提取出来。

4. 文件搜索：哈夫曼树可以应用于快速搜索文件数据的场景中。

通过构建文件的哈夫曼树，可以有效地进行关键字搜索，加快搜索速度。

5. 数据库索引：哈夫曼树可以用于数据库的索引结构中，如
B+树索引。

通过利用哈夫曼树的性质，将索引数据进行有序
排列，提高数据库的查询效率。

总之，哈夫曼树的应用非常广泛，不仅限于哈夫曼编码，还可
以应用于数据压缩、图像压缩、加密算法、文件搜索、数据库索引等领域。

2.9.1 哈夫曼树及应用哈夫曼树又称最优树（二叉树），是一类带权路径最短的树。

构造这种树的算法最早是由哈夫曼(Huffman)1952年提出，这种树在信息检索中很有用。

结点之间的路径长度：从一个结点到另一个结点之间的分支数目。

树的路径长度：从树的根到树中每一个结点的路径长度之和。

结点的带权路径长度：从该结点到树根之间的路径长度与结点上权的乘积。

树的带权路径长度：树中所有叶子结点的带权路径长度之和，记作：WPL为最小的二叉树就称作最优二叉树或哈夫曼树。

完全二叉树不一定是最优二叉树。

哈夫曼树的构造：（1）根据给定的n个权值{w1,w2,...,w n}构造n棵二叉树的集合F={T1,T2,...,T n}，其中Ti 中只有一个权值为w i的根结点，左右子树为空；（2）在F中选取两棵根结点的权值为最小的数作为左、右子树以构造一棵新的二叉树，且置新的二叉树的根结点的权值为左、右子树上根结点的权值之和。

（3）将新的二叉树加入到F中，删除原两棵根结点权值最小的树；（4）重复（2）和（3）直到F中只含一棵树为止，这棵树就是哈夫曼树。

例1：例2：结点的存储结构:构造哈夫曼树的算法说明：#define n /* 叶子总数 */#define m 2*n-1 /* 结点总数 */证：由性质3，叶子结点数 n0=n2+1，故哈夫曼树结点总数为 n0+n2=n0+(n0-1)=2*n0-1 例3 在解某些判定问题时，利用哈夫曼树获得最佳判定算法。

（a)WPL=0.05*1+0.15*2+0.4*3+0.3*4+0.1*4=3.15（b)(c)WPL=0.4*1+0.3*2+0.15*3+0.05*4+0.1*4=2.05WPL=0.05*3+0.15*3+0.4*2+0.3*2+0.1*2=2.2哈夫曼编码从哈夫曼树根结点开始，对左子树分配代码“0”，右子树分配代码“1”，一直到达叶子结点为止，然后将从树根沿每条路径到达叶子结点的代码排列起来，便得到了哈夫曼编码。

哈夫曼树及其应用路径长度树中一个结点到另一个结点之间的路径由这两个结点之间的分枝构成，路径上的分枝数目称为它的路径长度。

由树的定义可知，从根结点到达树的每个结点有且仅有一条路径。

我们曾规定树的根的层数为1，如果树中某个结点的层数为k ，则从树的根到该结点的路径长度为（k-1）。

例如，在图1（a ）中，从根A 到结点B 、C 、D 、E 、F 、G 、H 的路径长度分别为1、1、2、2、3、3、4。

树的路径长度是从树的根结点到树的各个结点的路径长度之和，记作PL 。

例如，图1所示的3棵二叉树的路径长度分别为：PL(a) = 0+1+1+2+2+3+3+4 = 6 PL(b) = 0+1+1+2+2+2+2+3 = 13 PL(c) = 0+1+1+2+2+2+2+3 = 13由于二叉树中第k 层的结点最多为2k-1个，而树的根到第k 层的结点的路径长度为k-1，换句话说，二叉树中路径长度为k-1的这样的结点最多有2k-1个。

显然，在n 个结点的各二叉树中，完全二叉树具有最小的路径长度。

例如，图1（b ）所示为完全二叉树，其路径长度是13。

但具有最小路径长度的不一定是完全二叉树。

例如，图1（c ）所示为非完全二叉树，它也具有最小路径长度。

一般来说，若深度为k 的n 个结点的二叉树具有最小路径长度，那么从根结点到第k-1层具有最多的结点数2k-1-1，余下的n-2k-1+1个结点在第k 层的任一位置上。

哈夫曼树首先我们考虑带权的二叉树。

假如给定一个有n 个权值的集合{w 1，w 2，…，w n }，其中wi ≥0（1≤i ≤n ）。

若T 是一棵有n 个叶子的二叉树，而且将权w 1，w 2，…，w n 分别赋给T 的n 个叶子，那么我们称T 是权w 1，w 2，…，w n 的二叉树。

叶子的带权路径长度为T 的根到该叶子之间的路径长度与该叶子中权的乘积。

n 个叶子的二叉树的带权路径长度定义为：∑==ni i i l w WPL 1其中：w i 为叶子i 的权，l i 为根结点到叶子i 之间的路径长度。

哈夫曼树的实际应用
哈夫曼树在实际中有许多应用，以下是一些例子：
1. 数据压缩：哈夫曼树常用于数据压缩算法，如哈夫曼编码。

哈夫曼编码是一种前缀编码，它可以将数据中的字符编码为二进制字符串，使得平均编码长度最短，从而达到数据压缩的效果。

2. 文件存储：在文件存储中，哈夫曼树可以用于数据存储和检索。

例如，可以使用哈夫曼树来存储文件索引，以便快速找到文件。

3. 图像处理：在图像处理中，哈夫曼树可以用于图像压缩和编码。

例如，可以使用哈夫曼树来编码图像中的像素值，从而减小图像文件的大小。

4. 通信网络：在通信网络中，哈夫曼树可以用于数据传输和调度。

例如，可以使用哈夫曼树来优化数据的传输路径和顺序，以提高网络传输的效率和可靠性。

5. 数据库优化：在数据库优化中，哈夫曼树可以用于索引和查询处理。

例如，可以使用哈夫曼树来构建索引，以便快速检索数据库中的数据。

总的来说，哈夫曼树在许多领域中都有广泛的应用，特别是在需要数据压缩、文件存储、图像处理、通信网络和数据库优化的领域中。

哈夫曼树及其应⽤1、基本概念a、路径和路径长度若在⼀棵树中存在着⼀个结点序列 k1，k2，……，kj，使得 ki是ki+1 的双亲（1<=i<j），则称此结点序列是从 k1 到 kj 的路径。

从 k1 到 kj 所经过的分⽀数称为这两点之间的路径长度，它等于路径上的结点数减1.b、结点的权和带权路径长度在许多应⽤中，常常将树中的结点赋予⼀个有着某种意义的实数，我们称此实数为该结点的权，(如下⾯⼀个树中的蓝⾊数字表⽰结点的权)结点的带权路径长度规定为从树根结点到该结点之间的路径长度与该结点上权的乘积。

c、树的带权路径长度树的带权路径长度定义为树中所有叶⼦结点的带权路径长度之和，公式为：其中，n表⽰叶⼦结点的数⽬，wi 和 li 分别表⽰叶⼦结点 ki 的权值和树根结点到 ki 之间的路径长度。

如下图中树的带权路径长度 WPL = 9 x 2 + 12 x 2 + 15 x 2 + 6 x 3 + 3 x 4 + 5 x 4 = 122d、哈夫曼树哈夫曼树⼜称最优⼆叉树。

它是 n 个带权叶⼦结点构成的所有⼆叉树中，带权路径长度 WPL 最⼩的⼆叉树。

如下图为⼀哈夫曼树⽰意图。

2、构造哈夫曼树假设有n个权值，则构造出的哈夫曼树有n个叶⼦结点。

n个权值分别设为 w1、w2、…、wn，则哈夫曼树的构造规则为：(1) 将w1、w2、…，wn看成是有n 棵树的森林(每棵树仅有⼀个结点)；(2) 在森林中选出两个根结点的权值最⼩的树合并，作为⼀棵新树的左、右⼦树，且新树的根结点权值为其左、右⼦树根结点权值之和；(3)从森林中删除选取的两棵树，并将新树加⼊森林；(4)重复(2)、(3)步，直到森林中只剩⼀棵树为⽌，该树即为所求得的哈夫曼树。

如：对下图中的六个带权叶⼦结点来构造⼀棵哈夫曼树，步骤如下：注意：为了使得到的哈夫曼树的结构尽量唯⼀，通常规定⽣成的哈夫曼树中每个结点的左⼦树根结点的权⼩于等于右⼦树根结点的权。

哈夫曼树算法用途哈夫曼树是一种常用的数据压缩算法，广泛应用于文件压缩、图像压缩、音频压缩等领域。

它可以根据数据的频率分布构建一颗最优的二叉树，从而实现数据的高效压缩和解压缩。

下面将从哈夫曼树的原理、构建方法和应用领域等方面进行详细阐述。

首先，我们来了解一下哈夫曼树的原理。

哈夫曼树是一颗带权路径长度最短的二叉树，其带权路径长度是指所有叶子结点的权值乘以其到根结点的路径长度之和。

对于一组给定的权值集合，构建哈夫曼树的过程是这样的：首先将权值按照从小到大的顺序排序，然后取权值最小的两个结点作为叶子结点，构建一个新的父节点，其权值为两个叶子结点的权值之和。

将这个新的父节点插入到原来的集合中，重复上述步骤直到只剩下一个根结点为止。

最终构建出的二叉树就是一颗哈夫曼树。

接下来，我们来介绍一下哈夫曼树的构建方法。

构建哈夫曼树的核心思想是贪心算法，即每次都选择权值最小的两个结点进行合并。

具体的构建步骤如下：1. 将待构建哈夫曼树的结点按照权值从小到大排序。

2. 创建一个空的哈夫曼树，将权值最小的两个结点作为叶子结点插入到树中，并创建一个新的父节点，其权值为这两个结点的权值之和。

3. 将这个新的父节点插入到原来的结点集合中，并将原来的两个结点从集合中删除。

4. 重复上述步骤，直到只剩下一个根结点为止，构建出的二叉树就是一颗哈夫曼树。

构建哈夫曼树的时间复杂度为O(nlogn)，其中n为叶子结点的个数。

由于每次都需要排序，所以效率较低。

为了提高效率，可以使用最小堆这种数据结构来快速选择权值最小的结点。

哈夫曼树的应用领域非常广泛。

其中最为重要的应用之一就是数据压缩。

在计算机存储和传输过程中，数据通常需要经过压缩以减小存储空间和传输带宽。

哈夫曼树作为一种高效的数据压缩算法，可以根据数据的频率分布来构建一个最优的编码表，将频率高的字符用较短的编码表示，而将频率低的字符用较长的编码表示，从而实现数据的高效压缩。

在文件压缩中，哈夫曼树可以根据不同字符的出现频率来构建一个相对最优的编码表，然后将文件中的字符按照这个编码表进行替换。

哈夫曼树hufferman构成原理应用及其数学证明哈夫曼树（Huffman Tree），又称最优树，它是一种常用的编码技术，它是一种十分高效的字符编码技术， 它主要是通过对字符按照出现频率高低进行分组，从而构成一颗树；每个字符的编码由树的层次顺序确定，字符越靠近根节点，编码越短，且编码长度与概率成正比，最后得出最优（最短）编码。

哈夫曼树构成原理：哈夫曼树构成原理是通过将信源字符重新按照概率顺序构成一棵有序树来实现的，即带有权值的叶子节点的树。

例如，某信源由四种字符A，B，C，D组成，出现的概率分别为p1，p2，p3，p4。

则可以构成一棵哈夫曼树。

首先，将四个字符依据概率从大到小重新排列，得到ABCD，依据概率大小选择A和B两个字符，以他们为叶子节点构成根节点，这样就分出了两颗子树。

接着将C和D两个字符以此作为叶子节点构成另外两棵子树，将他们与上面的根节点联接在一起，当初始树建立完毕，就得到了一棵哈夫曼树。

哈夫曼树数学证明：证明哈夫曼树是最优树：假设一棵信源树的叶子节点有n个，则此树的权重之和为：w1+w2+…+wn，其中wi是叶子节点i的权重，建立该信源树的目标是将其权重之和最小化，而在没有违反信源编码原理的前提下，树的最小权重之和也就是最优树的权重之和。

假设w1～wn分别为叶子节点1～n的权重，从大到小排列为w1，w2，…，wn，一棵以w1，w2，…，wn为叶子节点的最优树的权重之和为：T（w1，w2，…，wn）=w1+w2+…+wn+2（w1+w2）+2（w1+w2+w3）+……+2（w1+w2+…+wn-1）＝2（w1+w2+…+wn-1）+wn ＝2T（w1，w2，…，wn-1）+wn由上式可知，最优树的权重之和T（w1，w2，…，wn）是由T （w1，w2，…，wn-1）和wn组成的，也就是说，每次取出w1，w2，…，wn中的最大者wn作为树的一个节点，其余的作为树的另一个节点，而每一次节点的选取都是满足最优化条件的，因此一棵满足最优树条件的树就是哈夫曼树，而此树的权重之和也就是最优树的权重之和．从上述可以看出，哈夫曼树构成原理和哈夫曼树数学证明都支持哈夫曼树是最优树的观点，因此哈夫曼树是一种有效的编码技术。