广东省南华中学2016届高三数学天天练习21 文

南华中学高2016级文科数学天天练习（30）姓名：一、选择题：（1）设tan ,tan αβ是方程2320x x -+=的两个根,则tan()αβ+的值为（ ） （A ）3-（B ）1-（C ） 1（D ） 3（2）若函数[]()sin (0,2)3x f x ϕϕπ+=∈是偶函数,则ϕ=（ ）（A ）2π （B ）23π （C ）32π （D ）53π（3）在ABC ∆中,内角A ,B ,C 所对的边分别是,,a b c ,已知8=5b c ,=2C B ,则cos C =（ ）（A ）725（B ）725-（C ）725±（D ）2425二、填空题：（4）设ABC ∆的内角,,A B C 的对边分别为,,a b c ,且35cos ,cos ,3,513A B b ===则c =_____ .（5）函数xxy cos 2cos 2-+=的最大值为________.（6）设ABC ∆的内角,,A B C 所对的边为,,a b c ;则下列命题正确的是_____（填正确结论的序号） ①若2ab c >;则3C π<②若2a b c +>;则3C π<③若333a b c +=;则2C π<④若()2a b c ab +<;则2C π> ⑤若22222()2a b c a b +<;则3C π>三、解答题：（7）如图，平面直角坐标系xOy 中，,3ABC π∠= 6ADCp?,AC =，BCD ∆的面（Ⅰ）求AB 的长；（Ⅱ）若函数()sin()(0,0,)2f x M x M πωϕωϕ=+>><的图像经过,,A B C 三点，其中,A B 为()f x 的图像与x 轴相邻的两个交点，求函数()f x 的解析式.天天练30答案（1）A 【解析】tan tan 3tan tan 3,tan tan 2.tan()31tan tan 12αβαβαβαβαβ++==+===---(2) C 【解析】由[]()sin(0,2)3x f x ϕϕπ+=∈为偶函数可知，y 轴是函数()f x 图像的对称轴，而三角函数的对称轴是在该函数取得最值时取得，故3(0)sin13()3322f k k k Z ϕϕπππϕπ==±⇒=+⇒=+∈,而[]0,2ϕπ∈,故0k =时,32πϕ=. (3) A 【解析】∵8=5b c ,由正弦定理得8sin =5sin B C ,又∵=2C B ,∴8sin =5sin 2B B , 所以8s i B B B ,易知s i B ≠,∴4cos =5B ,2cos =cos 2=2cos 1C B B -=725.(4)145c = 【解析】由35412cos ,cos sin ,sin 513513A B A B ==⇒==,由正弦定理sin sin a b A B =得43sin 13512sin 513b A a B ⨯===, 由余弦定理2222142cos 25905605a cb bc A c c c =+-⇒-+=⇒=.(5) 3 【解析】22221(2cos )2cos ,cos 11,3113y y y x x x y y y ---=+=⇒-≤≤≤≤++ (6) 【解析】正确的是①②③①222221cos 2223a b c ab ab ab c C C ab ab π+-->⇒=>=⇒< ②2222224()()12cos 2823a b c a b a b a b c C C ab ab π+-+-++>⇒=>≥⇒< ③当2C π≥时,22232233c a b c a c b c a b ≥+⇒≥+>+与333a b c +=矛盾④取2,1a b c ===满足()2a b c ab +<得:2C π<⑤取2,1a b c ===满足22222()2a b c a b +<得:3C π<(7) 解：（Ⅰ）∵3ABCp?，6ADC p ?，∴6BCD p ?，23CBD p?，又∵BCD ∆，∴12sin23BCD S BD BC p D =鬃2BC == ∴2BC =. ……………………………………………………………………………2分在ABC D 中，AC =，3ABC p?，由余弦定理得：2222cos3AC AB BC AB BC p=+-?，即2174222A B A B =+-创， 整理得2230AB AB --=，………………………………………………………4分 ∴3AB =，或1AB =-(舍去)，∴AB 的长为3.………………………………5分（Ⅱ）由（Ⅰ）知，(2,0),(1,0),A B C -，∵函数()sin()(0,0,)2f x M x M πωϕωϕ=+>><的图像经过,,A B C 三点，其中,A B 为()f x 的图像与x 轴相邻的两个交点，∴函数()f x 的半个周期32T =，对称轴为12x =， ∴26T p w ==，∵0ω>，∴3pw =…………………………7分 ∴1,232k k Z p p j p ?=+?，∴,3k k Z p j p =+?， 又∵2πϕ<，∴3p j =，…………9分∴()sin()33f x M x p p=+，又∵(0)sin 3f M p ===，∴2M =，…………11分 ∴函数()f x 的解析式是()2sin()33f x x p p=+.………………………………12分。

南华中学高2016级文科数学天天练习（5）姓名:一、选择题：1。

函数)1ln(+=x y 与xy 1=的图像交点的横坐标所在区间为( ）A 。

(0,1)B 。

(1,2) C.(2,3)D 。

(3,4)2。

从某项综合能力测试中抽取100人的成绩，统计如表,则这100人成绩的标准差为( ）B ．3C ．5D ．853.e ,4=为单位向量，当e a ,的夹角为32π时，e a +在e a -上的投影为（ ）A 。

5B 。

154C 。

13D 。

7二、填空题：4。

已知直线1y kx =+与曲线3y x ax b =++切于点(1,3)，则b 的值为__________。

5。

函数4log )(2xx f =，等比数列{}n a 中，8852=⋅⋅a a a ，则=+++)(...)()(921a f a f a f __________.6.已知ABC 面积S 和三边,,a b c 满足:22(b c),8S ab c =--+=，则ABC 面积S 的最大值为 三、解答题:7.已知等差数列}{na 的公差不为零，其前n 项和为nS ，若5S =70，且2272,,a a a 成等比数列，(1）求数列}{na 的通项公式；（2）设数列⎭⎬⎫⎩⎨⎧n S 1的前n 项和为nT ，求证:8361<≤nT．南华中学高2016级文科数学天天练习（6）姓名：一、选择题：1。

执行如图所示的程序框图，输出的S 值为（ ）A ．2B ．4C ．8D ．162.若||2||||a b a b a=-=+，则向量a b +与a 的夹角为(）A ．6π B ．3π C ．32πD ．65π3。

函数)2||,0,0)(sin()(πφωφω<>>+=A x A x f 的部分图象如图示,则将()y f x =的图象向右平移6π个单位后，得到的图象解析式为（ ）A ．x y 2sin =B ．x y 2cos =C ．)322sin(π+=x y D ．)62sin(π-=x y二、填空题：4．若ABC ∆的三边长组成的集合是{}3,2，则ABC ∆的面积是 5.在等差数列{}na 中，912162aa =+，则数列{}na 的前11项和S 11等于 ．6.向量(1,0),(1,1)OA OB ==,O 为坐标原点，动点(,)P x y 满足0102OP OA OP OB ⎧≤⋅≤⎪⎨≤⋅≤⎪⎩,则点(,)Q x y y +构成图形的面积为 ．三、解答题：7.在△ABC 中，角A,B ，C 的对边分别为a ，b ，c ．已知C B C B cos cos 41)cos(2=+-（1）求角A 的大小；（2）若72=a ,△ABC 的面积为32，求c b +．南华中学高2016级文科数学天天练习（7）姓名：一、选择题：1.已知复数Z 满足(1)z 35i i -=+，则复数Z 在复平面内对应的点位于( )A 。

南华中学高2016级文科数学天天练习(1)姓名:一、选择题: 1.数列{}na 满足111n naa +=-，112a=则3a =（ )A ．12B ． 2C ． 1-D ． 12.从区间0,2π⎡⎤⎢⎥⎣⎦内随机取一个数x ，则3sin x <的概率为（ )A ．3 B ．23C ． 12D ． 133.若两个非零向量,a b →→满足2a b a b a →→→+=-=，则向量a b +与a b -的夹角是( ）A ．6π B ．3π C ．23πD ．56π 二、填空题： 4.设函数4()f x x ax =+，若曲线()y f x =在1x =处的切线斜率为1，则a =；5。

已知ABC 中，A 、B 、C的对边分别为,,a b c ，且2223ab c bc =+，则A= ；6. 如图,在ABC ∆中，120,2,1,BAC AB AC D ∠=︒==是边BC 上一点，2,DC BD =则AD BC ⋅=______________.三、解答题：7.已知(2cos ,sin ),(cos ,sin )a x x b x x x ==，设函数()f x a b =⋅。

(1）求()f x 图像的对称轴方程；（2）求()f x 在5,12ππ⎡⎤⎢⎥⎣⎦上的值域.南华中学高2016级文科数学天天练习（2）姓名：一、选择题： 1。

不等式1)2(log 22>++-x x的解集为（ ）A 、()0,2-B 、()1,1-C 、()1,0D 、()2,12.已知命题p ：函数()f x x a =+在(,1)-∞-上是单调函数,命题q ：函数()log (1),a g x x =+（0a >且1a ≠）在(1,)-+∞上是增函数。

则p ⌝是q 的(）A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既非充分也非必要条件3.已知函数)(x f 是定义在R 上的奇函数，对任意0,,≠+∈y x R y x ，都有0)()(>++yx y f x f ，若y x 2>，则（ ))2()(.y f x f A > )2()(.y f x f B ≥)2()(.y f x f C <)2()(.y f x f D ≤4.某公司为改善职工的出行条件，随机抽取50名职工，调查他们的居住地与公司的距离d ［单位:千米］。

南华中学高2016级文科数学天天练习（27）“20—21题” 姓名：1.已知椭圆2222:1(0)x y C a b a b+=>>的离心率为12，左、右焦点为12,F F ，点P 是椭圆C上任意一点，且12PF F ∆（1）求椭圆C 的方程；（2）过2F 作垂直于x 轴的直线l 交椭圆于,A B 两点（点A 在第一象限），,M N 是椭圆上位于直线l 两侧的动点，若MAB NAB ∠=∠，求证：直线MN 的斜率为定值．2.已知函数()()ln f x x x a x =+-，其中a 为常数。

（1）当1a =-时，求()f x 的极值；（2）若()f x 是区间1(,1)2内的单调递增函数，求实数a 的取值范围；（3）过坐标原点可以作几条直线与曲线()y f x =相切？请说明理由．题源自重庆一中高2016级2015-2016学年度高三上期第四次月考参考答案1．解：（1）由题12c a =①，12PF F ∆1232c b =②由方程组222122,1c a bc a b c a b c ⎧=⎪⎪⎪=⇒===⎨⎪=+⎪⎪⎩，所以椭圆方程为：22143x y += （2）3(1,)2A ，设1122(,)(,)M x y N x y 直线MN 方程为：y kx m =+，代入椭圆22143x y +=得：222(43)84120k x kmx m +++-=， 所以121222840,,4343km mx x x x k k -∆>+==++，又由题M N 、是椭圆上位于直线l 两侧的动点，若MAB NAB∠=∠，等价于：化简得：(21)(223)0k m k -+-=，所以当12k =时上式恒成立． 所以直线MN 的斜率为定值，且等于12． 另解：可以设直线AM 的斜率求,M N 的坐标，再求斜率．2．解：（1）当1a =时，2121(21)(1)()21(0)x x x x f x x x x x x----'=--==> 所以()f x 在区间(0,1)内单调，在区间(1,)+∞内单调递增，于是()f x 有极小值(1)0f =，无极大值．（2）易知1()2f x x a x '=--在区间1(,1)2内单调递增， 所以由题意可得1()20f x x a x '=--≥在1(,1)2内恒成立，即12a x x ≤-在1(,1)2内恒成立，所以min 1(2)a x x≤-，因为函数1()2h x x x =-在1(,1)2x ∈时单减， 所以()(1,1)h x ∈-所以1a ≤-，的数a 取值范围是(],1-∞．（3）设切点为2(,ln )t t at t +-，则切线方程为：21(2)()ln y t a x t t at t t=------，因为过原点，所在210(2)()ln t a t t at t t=------，化简得21ln 0t t -+=设2()1ln h t t t =-+则1()20h t t t'=+>，所以()h t 在(0,)+∞内单调递增，又(1)0h =，故方程21ln 0t t -+=有唯一实根1t =，所以满足条件的切线只有一条．。

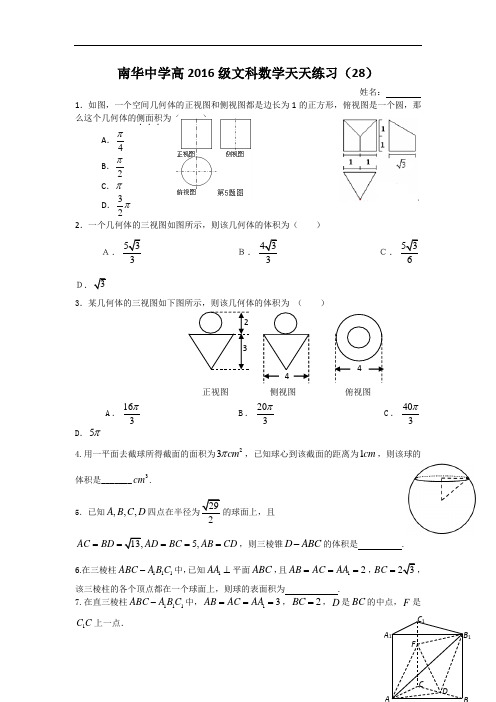
南华中学高2016级文科数学天天练习（28）姓名：1．如图，一个空间几何体的正视图和侧视图都是边长为1的正方形，俯视图是一个圆，那么这个几何体的侧面积．．．为（ ） A ．4πB ．2πC ．πD ．32π2．一个几何体的三视图如图所示，则该几何体的体积为（ ）Ａ．3 Ｂ．3 Ｃ．63．某几何体的三视图如下图所示，则该几何体的体积为 （ ）A ．163π B ．203π C ．403πD ．5π4.用一平面去截球所得截面的面积为23cm π，已知球心到该截面的距离为1cm ，则该球的体积是_______3cm .5．已知,,,A B C D的球面上，且5,AC BD AD BC AB CD ====，则三棱锥D ABC -的体积是 .6.在三棱柱111ABC A B C -中，已知1AA ⊥平面ABC ，且12A B A C A A ===，BC =该三棱柱的各个顶点都在一个球面上，则球的表面积为 .7.在直三棱柱111ABC A B C -中，13AB AC AA ===，2BC =，D 是BC 的中点，F 是1C C 上一点．正视图 侧视图 俯视图CDFA 1B 1C 1（Ⅰ）当2CF =时，证明：1B F ⊥平面ADF ； （Ⅱ）若D B FD 1⊥，求三棱锥1B ADF -的体积．南华中学高2016级文科数学天天练习（29）姓名：一、选择题：1．函数y ＝sin x sin ⎝⎛⎭⎫π2＋x 的最小正周期是( )A ．π2B ．2πC ．πD ．4π2．为了得到函数y ＝cos ⎝⎛⎭⎫2x ＋π3的图像，可将函数y ＝sin 2x 的图像( )A ．向左平移5π6B ．向右平移5π6C ．向左平移 5π12D ．向右平移5π123.已知3sin 5ϕ=，且2ϕπ⎛⎫∈π ⎪⎝⎭，，函数()sin()(0)f x x ωϕω=+>的图像的相邻两条对称轴之间的距离等于2π，则4f π⎛⎫⎪⎝⎭的值为（ ） （A ）35-（B ）45- （C ）35 （D ）45二、填空题：4．已知向量a ＝(sin θ，cos θ)，b ＝(2，－3)，且a ∥b ，则tan θ＝_____ ___． 5．已知α∈R ，sin α＋3cos α＝5，则tan2α＝______ __．6．将函数f (x )＝sin ⎝⎛⎭⎫3x ＋π4的图像向右平移π3个单位长度，得到函数y ＝g (x )的图像，则函数y ＝g (x )在区间⎣⎡⎦⎤π3，2π3上的最小值为_____ ___．三、解答题：7.已知a ，b ，c 是△ABC 中角A ，B ，C 的对边，且3c o s c o s B C +=23s i ns i n 2c o sB C A +．（Ⅰ）求角A 的大小；（Ⅱ ）若△ABC 的面积S =5b =，求sin sin B C 的值．南华中学高2016级文科数学天天练习（30）姓名：一、选择题：（1）设tan ,tan αβ是方程2320x x -+=的两个根,则tan()αβ+的值为（ ）（A ）3-（B ）1- （C ） 1 （D ） 3（2）若函数[]()sin (0,2)3x f x ϕϕπ+=∈是偶函数,则ϕ=（ ） （A ）2π （B ）23π （C ）32π （D ）53π（3）在ABC ∆中,内角A ,B ,C 所对的边分别是,,a b c ,已知8=5b c ,=2C B ,则cos C =（ ）（A ）725（B ）725-（C ）725±（D ）2425二、填空题：（4）设ABC ∆的内角,,A B C 的对边分别为,,a b c ,且35cos ,cos ,3,513A B b ===则c =_____ .（5）函数xxy cos 2cos 2-+=的最大值为________.（6）设ABC ∆的内角,,A B C 所对的边为,,a b c ;则下列命题正确的是_____（填正确结论的序号）①若2ab c >;则3C π<②若2a b c +>;则3C π<③若333a b c +=;则2C π<④若()2a b c ab +<;则2C π> ⑤若22222()2a b c a b +<;则3C π>三、解答题：（7）如图，平面直角坐标系xOy 中，,3ABC π∠= 6ADCp?,AC =BCD ∆的面（Ⅰ）求AB 的长；（Ⅱ）若函数()sin()(0,0,)2f x M x M πωϕωϕ=+>><的图像经过,,A B C 三点，其中,A B 为()f x 的图像与x 轴相邻的两个交点，求函数()f x 的解析式.南华中学高2016级文科数学天天练习（31）姓名：一、选择题：（1）在矩形ABCD 中，O 是对角线的交点，若O e e 则,3,521===（ ）（A ）)35(2121e e + （B ）)35(2121e e - (C ）)53(2121e e - （D ）)35(2112e e -（2）设向量b a ,满足10=+b a ，|6=-b a ，则=⋅b a ( ）（A ）1 （B ）2 （C ）3 （D ）5 （3）设四边形ABCD 为平行四边形，6=，4=.若点M ，N 满足，3=,2=，则NM AM ⋅=（ ）（A ）20 （B ）15 （C ）9 （D ）6（4）点O 是△ABC 所在平面内的一点，满足⋅=⋅=⋅，则点O 是△ABC的（ ）（A ）三个内角的角平分线的交点 （B ）三条边的垂直平分线的交点 （C ）三条中线的交点 （D ）三条高的交点（5）设0≤θ<2π，已知两个向量),sin ,(cos 1θθ==2OP ,sin 2(θ-)cos 2θ-则向量21P P 长度的最大值是（ ）（A ） 222+ （B ）31+ （C ）221+（D）322+ 二、填空题：（6）已知向量=a )1,6(，=b )21,4(-，直线l 过点A(3，－1)且与向量b a 2+垂直，则直线l的方程为 .（7）已知e 为单位向量，||a =4，e a 与的夹角为π32，则e a 在方向上的投影为 .三、解答题：（8）如图，在平行四边形ABCD 中，,E F 分别是BC,DC 的中点，G 为交点，若AB a =，AD b =.试以b a ,为基底表示.,,（9）设两向量21,e e 满足1,221==e e 21,e e 的夹角为060, 若向量t 2217e e +与向量+1e t 2e 的夹角为钝角, 求实数t 的取值范围.天天练28答案1．C 【析】：由几何体的三视图可知几何体为底面半径为21，高为1的圆柱，而圆柱侧面展开图为一个矩形，该矩形的长为底面圆的周长ππ=⨯212，高为1，所以该圆柱侧面积为ππ=⨯⨯=11s考点：空间几何体的三视图和直观图、空间几何体的表面积2．A 【析】：该几何体为一个三棱柱截去一个三棱锥，所以体积为22122-23⨯⨯. 考点：空间几何体的体积. 3.A 【析】：观察可知，该几何体为球、圆锥的组合体，球半径为1，圆锥底面半径为2，圆锥高为3，所以该几何体的体积为324116123333πππ⨯+⨯⨯=，故选A ． 考点：三视图，几何体的体积. 4.323π 分析:设截面圆半径为r ,则23r ππ=,23r =,球半径为R ,则222314R r d =+=+=,2R =,所以343233V R ππ==(3cm )5.解析：根据题意，可将三棱锥D ABC -补成一个长方体，如图所示设长方体从同一顶点出发的三条棱长分别为,,a b c ，则有222222222221332542429a c a a b b b c AB c a b c R ⎧+==⎪⎧+=⎪⎪⇒=⎨⎨+=⎪⎪=⎩⎪++==⎩所以11244324328323D ABC V a b c -=-⨯⨯⨯⨯⨯=⨯⨯-⨯⨯⨯=长方体.6. 20π 解析：由2,AB AC BC ===，根据余弦定理可求得1cos 2A ==-，所以sin A =，所以ABC ∆的外接圆的半径122r ===，设该圆的圆心为1O ，设球心为O ，根据对称性及球的性质可知，1OO ⊥平面ABC ，且11112OO AA ==所以球半径R OA ===球的表面积为24420R πππ=⨯=.7.（Ⅰ）证明：因为AB AC =，D 是BC 的中点，所以AD ⊥BC .在直三棱柱111ABC A B C -中，因为1B B ⊥底面ABC ，AD ⊂底面ABC ，所以AD ⊥1B B .因为BC ∩1B B ＝B ，所以AD ⊥平面11B BCC .因为1B F ⊂平面11B BCC ，所以AD ⊥1B F .在矩形11B BCC 中，因为11C F CD ==，112B C CF ==，所以Rt DCF ∆≌11Rt FC B ∆. 所以∠CFD ＝∠11C B F .所以∠1=90B FD .（或通过计算1FD B F ==1B D ,得到△1B FD 为直角三角形） 所以1B F FD ⊥. 因为AD ∩FD ＝D ，所以1B F ⊥平面ADF .（Ⅱ）解：因为1AD B DF ⊥平面，AD =D 是BC 的中点，所以1CD =. 在Rt △1B BD 中，1BD CD ==，13BB =，所以1B D ==.因为1FD B D ⊥，所以Rt CDF ∆∽1Rt BB D ∆．所以11DF CDB D BB =. 所以113DF ==．所以111113329B ADF B DFV S AD-∆=⋅=⨯=.天天练29答案1、C2、 C3、 B4、23-5、43-6、-7.解：（Ⅰ）由23c o s c o s23s i n s i n2c o sB C B C A+=+，得()23c o s22c o sB C A++=．即22cos3cos20A A+-=．即(2cos1)(cos2)0A A-+=．解得1cos2A=或cos2A=-（舍去）．因为0A<<π，所以Aπ=3．（Ⅱ）由1sin2S bc A===，得20bc=．因为5b=，所以4c=．由余弦定理2222cosa b c bc A=+-，得212516220=212a=+-⨯⨯，故a=根据正弦定理2sin sin sina b cRA B C===，得5sin sin sin sin7b cB C A Aa a=⨯=．天天练30答案（1）A【解析】tan tan3tan tan3,tan tan 2.tan()31tan tan12αβαβαβαβαβ++==+===---(2)C【解析】由[]()sin(0,2)3xf xϕϕπ+=∈为偶函数可知，y轴是函数()f x图像的对称轴，而三角函数的对称轴是在该函数取得最值时取得，故3(0)sin13()3322f k k k Zϕϕπππϕπ==±⇒=+⇒=+∈,而[]0,2ϕπ∈,故0k=时,32πϕ=.(3)A【解析】∵8=5b c,由正弦定理得8sin=5sinB C,又∵=2C B,∴8sin=5sin2B B, 所以8s iB B B,易知s iB≠,∴4cos=5B,2cos=cos2=2cos1C B B-=725.(4)145c=【解析】由35412cos,cos sin,sin513513A B A B==⇒==,由正弦定理sin sina bA B=得43sin13512sin513b AaB⨯===,由余弦定理2222142cos25905605a cb bc A c c c=+-⇒-+=⇒=.(5) 3 【解析】22221(2cos )2cos ,cos 11,3113y y y x x x y y y ---=+=⇒-≤≤≤≤++ (6) 【解析】正确的是①②③①222221cos 2223a b c ab ab ab c C C ab ab π+-->⇒=>=⇒< ②2222224()()12cos 2823a b c a b a b a b c C C ab ab π+-+-++>⇒=>≥⇒< ③当2C π≥时,22232233c a b c a c b c a b ≥+⇒≥+>+与333a b c +=矛盾④取2,1a b c ===满足()2a b c ab +<得:2C π<⑤取2,1a b c ===满足22222()2a b c a b +<得:3C π<(7) 解：（Ⅰ）∵3ABC p ?，6ADC p ?，∴6BCD p ?，23CBD p?，又∵BCD ∆12sin 23BCD S BD BC p D =鬃2BC == ∴2BC =. ……………………………………………………………………………2分在ABC D 中，AC =，3ABC p?，由余弦定理得：2222cos 3AC AB BC AB BC p=+-?，即2174222A B A B =+-创，整理得2230AB AB --=，………………………………………………………4分 ∴3AB =，或1AB =-(舍去)，∴AB 的长为3.………………………………5分（Ⅱ）由（Ⅰ）知，(2,0),(1,0),A B C -，∵函数()sin()(0,0,)2f x M x M πωϕωϕ=+>><的图像经过,,A B C 三点，其中,A B 为()f x 的图像与x 轴相邻的两个交点，∴函数()f x 的半个周期32T =，对称轴为12x =， ∴26T p w==，∵0ω>，∴3pw =…………………………7分∴1,232k k Z p p j p ?=+?，∴,3k k Z pj p =+?， 又∵2πϕ<，∴3p j =，…………9分∴()sin()33f x M x p p=+，又∵(0)sin 3f M M p ===2M =，…………11分∴函数()f x 的解析式是()2sin()33f x x p p=+.………………………………12分天天练31答案（1）选A ，=+=+==)(21)(21210BC DC BC AB AC C )35(2121e e +（2）选A , 解析：将上述两式平方后相减得，44=⋅b a（3）选C, ,43AD AB AM += ,3141AB AD CN CM MN +-=-=，所以,9)1693616(481)916(481)34(121)34(4122=⨯-⨯=-=-⋅+=⋅AD AB AD AB AD AB NM AM（4）选D ，0，即0）-（得,由=⋅=⋅⋅=⋅CA OB OC OA OB OC OB OB OA ,AC OB ⊥所以同理可得.三条高的交点是则点,,ABC O BC OA AB OC ∆⊥⊥（5）选A ，22)cos sin 2()sin cos 2(θθθθ--+--===))4sin(22(2πθ+-，时，达到最大值。

南华中学高2016级文科数学天天练习（30）姓名：一、选择题：（1）设tan ,tan αβ是方程2320x x -+=的两个根,则tan()αβ+的值为（ ） （A ）3-（B ）1-（C ） 1（D ） 3（2）若函数[]()sin (0,2)3x f x ϕϕπ+=∈是偶函数,则ϕ=（ ） （A ）2π （B ）23π （C ）32π （D ）53π（3）在ABC ∆中,内角A ,B ,C 所对的边分别是,,a b c ,已知8=5b c ,=2C B ,则cos C =（ ）（A ）725（B ）725-（C ）725±（D ）2425二、填空题：（4）设ABC ∆的内角,,A B C 的对边分别为,,a b c ,且35cos ,cos ,3,513A B b ===则c =_____ .（5）函数xxy cos 2cos 2-+=的最大值为________.（6）设ABC ∆的内角,,A B C 所对的边为,,a b c ;则下列命题正确的是_____（填正确结论的序号）①若2ab c >;则3C π<②若2a b c +>;则3C π<③若333a b c +=;则2C π<④若()2a b c ab +<;则2C π> ⑤若22222()2a b c a b +<;则3C π>三、解答题：（7）如图，平面直角坐标系xOy 中，,3ABC π∠= 6ADCp?,AC =BCD ∆的面（Ⅰ）求AB 的长；（Ⅱ）若函数()sin()(0,0,)2f x M x M πωϕωϕ=+>><的图像经过,,A B C 三点，其中,A B 为()f x 的图像与x 轴相邻的两个交点，求函数()f x 的解析式.天天练30答案（1）A 【解析】tan tan 3tan tan 3,tan tan 2.tan()31tan tan 12αβαβαβαβαβ++==+===---(2) C 【解析】由[]()sin(0,2)3x f x ϕϕπ+=∈为偶函数可知，y 轴是函数()f x 图像的对称轴，而三角函数的对称轴是在该函数取得最值时取得，故3(0)sin13()3322f k k k Z ϕϕπππϕπ==±⇒=+⇒=+∈,而[]0,2ϕπ∈,故0k =时,32πϕ=. (3) A 【解析】∵8=5b c ,由正弦定理得8sin =5sin B C ,又∵=2C B ,∴8sin =5sin 2B B ,所以8s i B B B ,易知si B ≠,∴4cos =5B ,2cos =cos 2=2cos 1C B B -=725.(4)145c = 【解析】由35412cos ,cos sin ,sin 513513A B A B ==⇒==, 由正弦定理sin sin a b A B =得43sin 13512sin 513b A a B ⨯===, 由余弦定理2222142cos 25905605a cb bc A c c c =+-⇒-+=⇒=.(5) 3 【解析】22221(2cos )2cos ,cos 11,3113y y y x x x y y y ---=+=⇒-≤≤≤≤++ (6) 【解析】正确的是①②③①222221cos 2223a b c ab ab ab c C C ab ab π+-->⇒=>=⇒< ②2222224()()12cos 2823a b c a b a b a b c C C ab ab π+-+-++>⇒=>≥⇒< ③当2C π≥时,22232233c a b c a c b c a b ≥+⇒≥+>+与333a b c +=矛盾④取2,1a b c ===满足()2a b c ab +<得:2C π<⑤取2,1a b c ===满足22222()2a b c a b +<得:3C π<(7) 解：（Ⅰ）∵3ABCp?，6ADC p ?，∴6BCD p ?，23CBD p ?，又∵BCD ∆12sin 23BCDS BD BC p D =鬃24BC == ∴2BC =. ……………………………………………………………………………2分在ABC D 中，AC =，3ABC p ?， 由余弦定理得：2222cos3AC AB BC AB BC p =+-?，即2174222AB A B =+-创， 整理得2230AB AB --=，………………………………………………………4分 ∴3AB =，或1AB =-(舍去)，∴AB 的长为3.………………………………5分（Ⅱ）由（Ⅰ）知，(2,0),(1,0),A B C -， ∵函数()sin()(0,0,)2f x M x M πωϕωϕ=+>><的图像经过,,A B C 三点，其中,A B 为()f x 的图像与x 轴相邻的两个交点，∴函数()f x 的半个周期32T =，对称轴为12x =， ∴26T p w==，∵0ω>，∴3pw =…………………………7分∴1,232k k Z p p j p ?=+?，∴,3k k Z pj p =+?， 又∵2πϕ<，∴3p j =，…………9分∴()sin()33f x M x p p=+，又∵(0)sin 32f M M p ===2M =，…………11分∴函数()f x 的解析式是()2sin()33f x x p p=+.………………………………12分。

南华中学高2016级文科数学天天练习（13)姓名:一、选择题：1．给定空间中的直线l 及平面a ，条件“直线l 与平面a 内无数条直线都垂直“是”直线l 与平面a 垂直"的（ ）A ．充要条件B ．充分不必要条件C ．必要不充分条件D ．既不充分又不必要条件2．已知三棱锥的三视图如右图所示，则它的外接球的表面积为（ )A ．π16B ．π8C ．π4D ．π23．已知PA 垂直于ABC ∆所在的平面,5==AC AB ，6=BC ，3=PA ，则A 到平面PBC 的距离为（ ）A ．4B ．15C ．53D ．512二、填空题:4．将函数()sin(3)4f x x π=+的图象向右平移3π个单位长度，得到函数()x g y =的图象,则函数()x g y =在⎥⎦⎤⎢⎣⎡323ππ，上的最小值为 ．5．一个几何体的正视图为一个三角形，则这个几何体可能是下列几何体中的 ．(填入所有可能的几何体前的编号)①三棱锥;②四棱锥； ③三棱柱；④四棱柱;⑤圆锥；⑥圆柱．6．已知任何一个三次函数()()320f x axbx cx d a =+++≠都有对称中心()()00x f x M ，,记函数()x f 的导函数为()x f '，()x f '的导函数为()x f ''，则有()0''0=x f ，若函数()233x x x f -=,则=⎪⎭⎫ ⎝⎛+⋯+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛20164031201632016220161f f f f .三、解答题：7．如图:在四棱锥ABCD P -中，底面ABCD 是平行四边形，⊥BC 平面PAB ，AB PA ⊥,M 为PB 中点，2==AD PA ，1=AB ．（1）求证：∥PD 面ACM ;(2）求PMCD V-．南华中学高2016级文科数学天天练习(14）姓名：一、选择题：1。

《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有委米依垣内角,下周八尺，高五尺。

南华中学高2016级文科数学天天练习（34）姓名：一、选择题：1．已知数列{}na 满足n n a n na a2,111+==+，则此数列的通项公式na 等于（ ）（A ）2)1(2+n （B ）)1(2+n n （C ）121-n（D ）121-n 2.设等差数列}{na 的前n 项和为,nS 且满足,0,01615<>S S则15152211,,,a S a S a S 中最大的项为（ ）.A66a S.B77a S.C 99a S.88a S3。

已知正项等比数列{}na 满足:7652aa a =+,若存在两项,m n a a 14a =，则14mn+的最小值为( ）A 32B ．53C ．256D ．不存在二、填空题:4．在△ABC 中，tan A 是以－4为第三项，4为第7项的等差数列的公差,tan B 是以13为第三项,9为第六项的等比数列的公比，则C= ．5．已知数列{a n ｝的前n 项和S n ＝3n 2－2n ＋1，则其通项公式为________________．6．设数列｛a n ｝中,a 1＝2，a n ＋1＝a n ＋n ＋1，则通项a n ＝________。

三、解答题:7．数列{na ｝的前n 项和为nS ，且满足11a=,2(1)n n S n a =+.（1）求{na ｝的通项公式; （2)求和T n =1211123(1)na a n a ++++。

南华中学高2016级文科数学天天练习（35）姓名:一、填空题：1．已知数列｛a n ｝的前n 项和为S n ,且S n ＝2a n －1(n ∈N ＊），则a 5等于( )A ．－16B ．16C ．31D ．322．若等比数列{}na 满足0,1,2,3nan >=……且25252(3)n n a a n -⋅=≥，则当1n ≥时，2123221log log log n a a a -+++=( ）A ．(21)n n -B ．2(1)n +C ．2nD ．2(1)n -二、填空题:3．数列｛a n }中，a 1＝1，a n ＋1＝3a n ＋2，则它的一个通项公式为a n＝________.4．在数列{a n ｝中，a 1＝1，前n 项和S n ＝错误!a n ，则｛a n ｝的通项公式为________．5．已知数列{a n ｝满足a 1＝1，a n ＝错误!·a n －1(n ≥2)，则a n ＝________. 三、解答题：6．已知数列{}n a 中，12a=，且当2n ≥时,1220n n n a a ---=(1）求数列{}na 的通项公式；（2）若{}na 的前n 项和为nS ，求nS .7．设数列{}na 的前n 项和为,nS 已知11,a=142n n S a +=+(Ⅰ）设12nn n b a a +=-，证明数列{}n b 是等比数列；(Ⅱ)求数列{}n a 的通项公式.天天练34参考答案1.B 2。

南华中学高2016级文科数学天天练习（21）姓名：一、选择题：1．若函数cos 2y x =与函数)2sin(φ+=x y 在⎥⎦⎤⎢⎣⎡40π，上的单调性相同，则ϕ的一个值为（ ）A ．6πB ．4πC ．43πD ．23π 2．已知两定点(2,0),(1,0)A B -，若动点P 满足||2||PA PB =，则点P 的轨迹所包围的图形的面积为（ ）（A ）π （B ）4π （C ）8π （D ）9π3.如图，12F F 、是双曲线2222-=1(>0,>0)x y a b a b的左、右焦点，过1F 的直线l 与双曲线的左右两支分别交于点A 、B 两点．若2A B F ∆为等边三角形，则双曲线的离心率为（ ）A ．4B ．3D 二、填空题：4.设函数24,0()3,0x x f x x x ⎧->=⎨--<⎩，若()(1)f a f >，则实数a 的取值范围是_____________．5.等比数列{}n a 的公比大于1，514215,6a a a a -=-=，则3a ＝____________．6.设()f x '和()g x '分别是函数()f x 和()g x 的导函数，若()()0f x g x ''⋅≤在区间I 上恒成立，则称函数()f x 和()g x 在区间I 上单调性相反．若函数31()23f x x a x =-与函数2()2g x x b x =+在开区间(,),a b a >上单调性相反，则b a -的最大值等于 ． 三、解答题：7.如图，四棱锥P ABCD -，底面ABCD 是边长为2的菱形，60ABC ∠=，M 为侧棱PD的三等分点（靠近D 点），O 为,AC BD 的交点，且PO ⊥面ABCD ，PO =。

（1）若在棱PD 上存在一点N ，且//BN AMC 面，确定点N 的位置，并说明理由； （2）求点B 到平面MAC 的距离。

南华中学高2016级文科数学天天练习（26）“17—19题”+”三选一”模拟题 姓名：1.如图，ABC ∆，4B π=，角A 的平分线AD 交BC 于点D，设,sin BAD αα∠==； （1）求sin BAC ∠和sin C ；（2）若28BA BC =，求AC 的长．2.央视记者柴静的《穹顶之下》的播出，让大家对雾霾天气的危害有了更进一步的认识，对于雾霾天气的研究也渐渐活跃起来，某研究机构对春节燃放烟花爆竹的天数x 与雾霾天数y 进行统计分析，得出下表数据．（1）请画出上表数据的散点图；（2）请根据上表提供的数据，用最小二乘法求出y 关于x 的线性回归直线方程ˆˆˆy bx a=+；（3）试根据（2）求出线性回归方程，预测燃放烟花爆竹的天数为9的雾霾天数．（相关公式1221ˆˆˆ,ni ii ni i x y nx ybay bx x nx==-==--∑∑）3.如图，四边形ABCD 为矩形，SA ⊥平面ABCD ，E F 、分别是SC SD 、的中点，2,SA AD ==，AB =。

（1）求证：SD ⊥平面AEF ；（2）求三棱锥F AED -的体积．4.（三选一）（1）如图，AB 是圆O 的一条切线，切点为B ，直线ADE CFD CGE 、、都是圆O 的割AC ．cos 2sin x r y r θθ⎧=+⎪⎪⎨⎪=+⎪⎩（θ为参数，0r >），l 的极坐标方程为sin()14πρθ+=，r 的值．()8()f x a a R <∈的解集不是空集。

（I ）求实数a 的取值范围；（II ）求24a a+的最小值．题源自重庆一中高2016级2015-2016学年度高三上期第四次月考参考答案1．解：（1）254sin sin 22sin cos2555BAC ααα∠====，32472sin sin()sin cos cos sin 252510C B A B A B A =+=+=+=， （2）由28cos282824BA BC AB BC AB BC π=⇒=⇒=且72sin 104sin 85AB C BC A ===，所以解得7,AB BC ==，由余弦定理得：2222cos 49325625AC AB BC AB BC B =+-=+-=，所以5AC =2．解：（1）散点图如图所示： （2）4142537586106i i i x y ==⨯+⨯+⨯+⨯=∑，457864x +++==，235644y +++==，42222214578154ii x ==+++=∑，则12221ˆˆ4106464ˆ1154464ni ii nii x y xybxx =-=--⨯⨯===-⨯-∑∑, ˆ462a y bx=-=-=-，故线性回归方程为ˆˆˆ2y bx a x =+=-， （3）由线性回归方程可以预测，燃烧烟花爆竹的天数为9的雾霾天数为7天．3．解：（1）∵SA AD =，F 为SD 的中点，∴SD AF ⊥， ∵SA ⊥平面ABCD ，AB ⊂平面ABCD ，∴AB SA ⊥∵AB AD ⊥，SA AD 、是平面SAD 内的两条相交直线，∴AB SAD ⊥平面， ∵SD SAD ⊂平面，∴SD AB ⊥，∵//EF AB ，∴SD EF ⊥ ∵AF EF 、是平面AEF 内的两条相交直线∴SD ⊥平面AEF （2）111162233222F AED E AFD AFD DC V V S EF --∆==== 4.（1）证明：∵AB 为切线，AE 为割线，∴2AB AD AE =， 又∵AC AB =，∴2AD AE AC =，∴AD ACAC AE=，又∵EAC CAD ∠=∠， ∴ADCACE ∆∆，∴ADC ACE ∠=∠，又∵ADC EGF ∠=∠，∴EGF ACE ∠=∠，∴//GF AC ．（2）解：圆C 的参数方程为cos 22x ry θ⎧=+⎪⎪⎨⎪=⎪⎩（θ为参数，0r >），消去参数θ得：222(((0)22x y r r +++=>2，半径r ，0x y +=，0=的距离为2d ==，3dr +=，∴3321r d =-=-= ． ()min2108x x a -+-<，8=，∴881a a <⇒>（II ）1a >时，224422a a a a a +=++，22432222a a a a ++≥= 当且仅当242a a =，即2a =时等号成立，所以24a a+的最小值为3．。