应用回归分析-实用回归分析

数据分析方法：回归分析实用指南引言数据分析在当今社会中扮演着至关重要的角色。

通过收集、整理和分析数据，我们可以获得有关特定问题或现象的深入洞察。

回归分析是一种常用的统计分析方法，可以帮助我们理解变量之间的关系，并预测未来的趋势。

本文将为您介绍回归分析的概念、应用和常见方法，希望能够为您在实际应用中提供一些有用的指导。

什么是回归分析？回归分析是一种用于研究变量之间关系的统计方法。

它通过建立一个数学模型来描述自变量（独立变量）与因变量（依赖变量）之间的关系。

回归分析可以帮助我们理解变量之间的关联性，从而探索隐藏在数据背后的规律。

回归分析的应用领域回归分析在各个领域都有广泛的应用，以下是一些常见的应用领域：1. 经济学在经济学中，回归分析被用来研究各种经济变量之间的关系，如GDP与投资、通货膨胀与失业率等。

通过回归分析，经济学家可以预测未来的经济趋势，为政府和企业提供决策支持。

2. 市场营销在市场营销领域，回归分析被广泛应用于市场调研和销售预测。

通过分析市场数据和消费者行为，市场营销人员可以确定哪些因素对产品销售额产生积极影响，并相应地调整营销策略。

3. 医学研究医学研究中也常用回归分析来探索疾病与生活方式、遗传因素等之间的关系。

通过回归分析，医生和研究人员可以找到影响疾病发生和发展的风险因素，从而提供更有效的预防和治疗方法。

4. 社会科学回归分析在社会科学研究中也是一个重要的工具。

通过回归分析，社会科学家可以研究教育、犯罪、就业等不同社会现象之间的关系，从而为社会政策制定提供依据。

简单线性回归分析在回归分析中，最简单的一种形式是简单线性回归分析。

在简单线性回归中，我们只考虑一个自变量和一个因变量之间的关系。

1. 模型表达式简单线性回归模型的表达式为：Y=β0+β1X+ɛ其中，Y是因变量，X是自变量，β0和β1是回归系数，ɛ是误差项。

2. 回归系数解释回归系数β0和β1分别表示截距和斜率。

截距β0表示当自变量X为0时，因变量Y 的预测值。

回归分析与相关分析的概念与应用回归分析和相关分析是统计学中常用的两种数据分析方法，它们可以帮助我们理解和解释变量之间的关系。

本文将介绍回归分析和相关分析的概念以及它们在实际应用中的用途。

一、回归分析的概念与应用回归分析是一种用于研究变量之间关系的方法。

它通过建立一个数学模型来描述自变量与因变量之间的关系，并使用统计方法对模型进行评估。

在回归分析中，我们需要选择一个合适的回归模型，并利用样本数据来估计模型参数。

回归分析可以应用于各种场景，例如市场营销、经济预测和医学研究等。

以市场营销为例，我们可以使用回归分析来研究广告投入与销售额之间的关系，从而制定更有效的营销策略。

此外，回归分析还可以用于预测未来的趋势和模式，帮助决策者做出准确的预测。

二、相关分析的概念与应用相关分析是用来衡量两个变量之间关系强度的统计方法。

它可以告诉我们这两个变量是否呈现线性相关，并给出相关系数来表示相关程度。

相关系数的取值范围是-1到1，当相关系数接近于-1时，表示负相关；当相关系数接近于1时，表示正相关；当相关系数接近于0时，表示无相关关系。

相关分析被广泛应用于各个领域，例如社会科学研究、金融分析和环境监测等。

在社会科学研究中，我们可以利用相关分析来研究教育水平与收入之间的关系，以及人口密度与犯罪率之间的关系。

通过分析相关性，我们可以发现变量之间的内在联系，进而做出有针对性的政策或决策。

三、回归分析与相关分析的联系与区别回归分析和相关分析都是用来研究变量之间关系的统计方法，但它们有一些区别。

首先，回归分析关注的是因变量与自变量之间的关系，并通过建立模型来预测因变量的取值。

而相关分析则更加关注变量之间的相关程度，并不涉及因果关系的解释。

其次，回归分析假设因变量与自变量之间存在一种函数关系，而相关分析只是衡量两个变量之间的相关性，并不要求存在具体的函数形式。

因此，回归分析可以进行更加深入的解释和预测，而相关分析则更加简单直观。

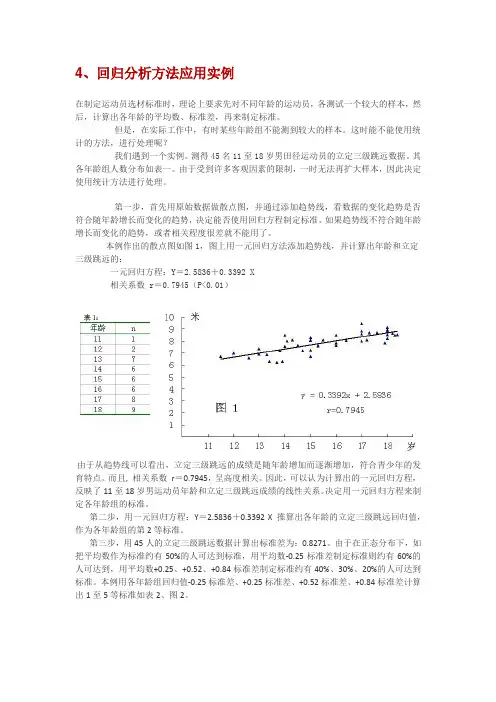
4、回归分析方法应用实例在制定运动员选材标准时，理论上要求先对不同年龄的运动员，各测试一个较大的样本，然后，计算出各年龄的平均数、标准差，再来制定标准。

但是，在实际工作中，有时某些年龄组不能测到较大的样本。

这时能不能使用统计的方法，进行处理呢？我们遇到一个实例。

测得45名11至18岁男田径运动员的立定三级跳远数据。

其各年龄组人数分布如表一。

由于受到许多客观因素的限制，一时无法再扩大样本，因此决定使用统计方法进行处理。

第一步，首先用原始数据做散点图，并通过添加趋势线，看数据的变化趋势是否符合随年龄增长而变化的趋势，决定能否使用回归方程制定标准。

如果趋势线不符合随年龄增长而变化的趋势，或者相关程度很差就不能用了。

本例作出的散点图如图1，图上用一元回归方法添加趋势线，并计算出年龄和立定三级跳远的：一元回归方程：Y＝2.5836＋0.3392 X相关系数 r＝0.7945（P<0.01）由于从趋势线可以看出，立定三级跳远的成绩是随年龄增加而逐渐增加，符合青少年的发育特点。

而且, 相关系数r＝0.7945，呈高度相关。

因此，可以认为计算出的一元回归方程，反映了11至18岁男运动员年龄和立定三级跳远成绩的线性关系。

决定用一元回归方程来制定各年龄组的标准。

第二步，用一元回归方程：Y＝2.5836＋0.3392 X 推算出各年龄的立定三级跳远回归值，作为各年龄组的第2等标准。

第三步，用45人的立定三级跳远数据计算出标准差为：0.8271。

由于在正态分布下，如把平均数作为标准约有50%的人可达到标准，用平均数-0.25标准差制定标准则约有60%的人可达到，用平均数+0.25、+0.52、+0.84标准差制定标准约有40%、30%、20%的人可达到标准。

本例用各年龄组回归值-0.25标准差、+0.25标准差、+0.52标准差、+0.84标准差计算出1至5等标准如表2、图2。

2、应用方差分析方法进行数据统计分析的研究。

第一章习题1.1变量间统计关系和函数关系的区别是什么？1.2回归分析与相关分析的区别和联系是什么？1.3回归模型中随机误差项的意义是什么？1.4线性回归模型中的基本假设是什么？1.5回归变量设置的理论依据是什么？在设置回归变量时应注意哪些问题？1.6收集、整理数据包括哪些基本内容？1.7构造回归理论模型的基本依据是什么？1.8为什么要对回归模型进行检验？1.9回归模型有哪几个方面的应用？1.10为什么强调运用回归分析研究经济问题要定性分析和定量分析相结合？第二章 习题2.1一元线性回归模型有哪些基本假定？ 2.2 考虑过原点的线性回归模型1,1,,i i i y x i n βε=+=误差1,,n εε仍满足基本假定。

求1β的最小二乘估计。

2.3证明（2.27）式，10nii e==∑，10ni i i x e ==∑。

2.4回归方程01Ey x ββ=+的参数01,ββ的最小二乘估计与极大似然估计在什么条件下等价？给出证明。

2.5 证明0ˆβ是0β的无偏估计。

2.6 证明(2.42)式 ()()222021,i x Var n x x βσ⎡⎤=+⎢⎥-⎢⎥⎣⎦∑成立 2.7 证明平方和分解式SST SSR SSE =+2.8 验证三种检验的关系，即验证：（1）t ==（2）2212ˆ1ˆ2xx L SSR F t SSE n βσ===-2.9 验证（2..63）式：()()221var 1i i xx x x e n L σ⎡⎤-=--⎢⎥⎢⎥⎣⎦2.10 用第9题证明()2211ˆˆ2n i ii y y n σ==--∑是2σ的无偏估计。

2.11* 验证决定系数2r 与F 值之间的关系式 22Fr F n =+-以上表达式说明2r 与F 值是等价的，那么我们为什么要分别引入这两个统计量，而不是只使用其中的一个。

2.12* 如果把自变量观测值都乘以2，回归参数的最小二乘估计0ˆβ和1ˆβ会发生什么变化？如果把自变量观测值都加上2，回归参数的最小二乘估计0ˆβ和1ˆβ会发生什么变化？ 2.13 如果回归方程01ˆˆˆy x ββ=+相应的相关系数r 很大，则用它预测时，预测误差一定较小。

回归分析的应用及回归分析的类型什么是回归分析？正确问题的近似答案要比近似问题的精确答案更有价值这正是回归分析所追求的目标，它是最常用的预测建模技术之一，有助于在重要情况下做出更明智的决策。

回归分析是作为数据科学家需要掌握的第一个算法。

它是数据分析中最常用的预测建模技术之一。

即使在今天，大多数公司都使用回归技术来实现大规模决策。

要回答“什么是回归分析”这个问题，我们需要深入了解基本面。

简单的回归分析定义是一种用于基于一个或多个独立变量（X）预测因变量（Y）的技术。

经典的回归方程看起来像这样：等式中，hθ（x）是因变量Y，X是自变量，θ0是常数，并且θ1是回归系数。

回归分析的应用回归分析有三个主要应用：•解释他们理解困难的事情。

例如，为什么客户服务电子邮件在上一季度有所下降。

•预测重要的商业趋势。

例如，明年会要求他们的产品看起来像什么？•选择不同的替代方案。

例如，我们应该进行PPC（按点击付费）还是内容营销活动？不同类型的回归分析技术有许多可用的回归技术，不同的技术更适合于不同的问题。

回归分析技术的类型基于：•自变量的数量（1,2或更多）•因变量的类型（分类，连续等）•回归线的形状主要类型的回归分析1. 线性回归线性回归是最常用的回归技术。

线性回归的目的是找到一个称为Y的连续响应变量的方程，它将是一个或多个变量（X）的函数。

因此，线性回归可以在仅知道X时预测Y的值。

它不依赖于任何其他因素。

Y被称为标准变量，而X被称为预测变量。

线性回归的目的是通过点找到称为回归线的最佳拟合线。

这就是数学线性回归公式/等式的样子：在上面的等式中，hθ（x）是标准变量Y，X是预测变量，θ0是常数，并且θ1是回归系数线性回归可以进一步分为多元回归分析和简单回归分析。

在简单线性回归中，仅使用一个独立变量X来预测因变量Y的值。

另一方面，在多元回归分析中，使用多个自变量来预测Y，当然，在这两种情况下，只有一个变量Y，唯一的区别在于自变量的数量。