(实验2)多元回归分析实验报告

计量经济学实验报告多元线性回归、多重共线性、异方差实验报告、研究目的和要求:随着经济的发展，人们生活水平的提高，旅游业已经成为中国社会新的经济增长点。

旅游产业是一个关联性很强的综合产业，一次完整的旅游活动包括吃、住、行、游、购、娱六大要素，旅游产业的发展可以直接或者间接推动第三产业、第二产业和第一产业的发展。

尤其是假日旅游，有力刺激了居民消费而拉动内需。

2012年，我国全年国内旅游人数达到30.0亿人次，同比增长13.6%，国内旅游收入2.3万亿元，同比增长19.1%。

旅游业的发展不仅对增加就业和扩大内需起到重要的推动作用，优化产业结构，而且可以增加国家外汇收入，促进国际收支平衡，加强国家、地区间的文化交流。

为了研究影响旅游景区收入增长的主要原因，分析旅游收入增长规律，需要建立计量经济模型。

影响旅游业发展的因素很多，但据分析主要因素可能有国内和国际两个方面，因此在进行旅游景区收入分析模型设定时，引入城镇居民可支配收入和旅游外汇收入为解释变量。

旅游业很大程度上受其产业本身的发展水平和从业人数影响，固定资产和从业人数体现了旅游产业发展规模的内在影响因素，因此引入旅游景区固定资产和旅游业从业人数作为解释变量。

因此选取我国31个省市地区的旅游业相关数据进行定量分析我国旅游业发展的影响因素。

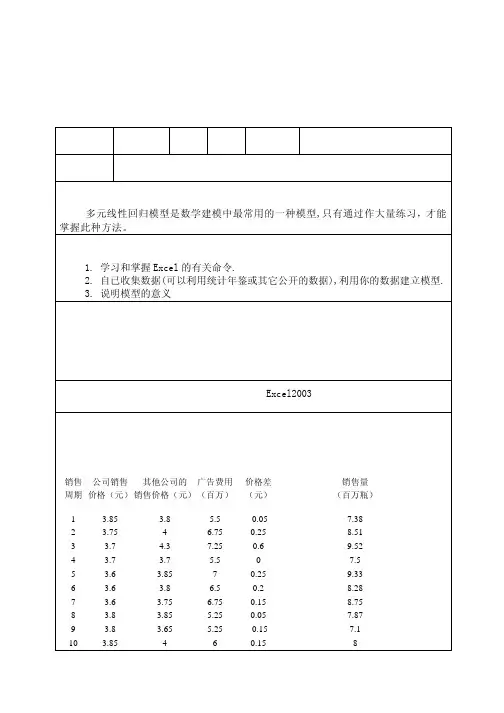
二、模型设定根据以上的分析，建立以下模型57丫=仇+ B1X 1+ 伍X 2+ B 3X 3+ 34 X 4 +Ut参数说明：旅游景区营业收入/万元X 1 旅游业从业人员/人 X 2 旅游景区固定资产/万元 X 3 旅游外汇收入/万美元 X 4城镇居民可支配收入/元收集到的数据如下（见表 2.1）:表2.1 2011年全国旅游景区营业收入及相关数据（按地区分） 地区 北 京 天 津 河 北 山 西内蒙 古辽 丿jA吉营业收入145249.0148712.3182226.8729465.0 70313.0 25665.3 20389.3 从业人 数1454 66 247879645771 3626 64812906 固定资产694252.393529.67 420342.7121809.7206819.146573.27 87827.16外汇收入可支配 收入5416017555 447655671967097 2713138528 32903. 0326920. 8618292. 2318123. 8720407.20466. 8417796.林0 6 57 黑龙38367.8 3034 137426.215696.91762江 1 1 7 18 上194762. 9110 563007.4 57511 36230. 海 3 6 4 8 48 江316051. 1401 1195000. 56529 26340. 苏65 54 60 7 73 浙385976. 1324 1110975. 45417 30970. 江92 59 20 3 68 安79562.7 5584 139769.0 11791 18606. 徽 5 0 2 8 13 福155378. 8030 151897.6 36344 24907. 建95 3 9 4 40 江54961.6 4179 17494.85528.05 41500西 6 1 87 山116995. 1430 327733.2 25507 22791. 东67 26 9 6 84 河222108. 7016 482005.3 18194.54903南33 4 2 80 湖104565. 6276 243794.618373.94018北58 7 2 87 湖118180. 806110143 18844.257226.7南87 5 4 05 广476345. 2265 1160675. 13906 26897. 东50 39 4 19 48 广66195.5 4987 143982.0 10518 18854. 西 5 6 3 8 06 海29081.6 3075 18368.70386.55 37615南0 9 95 重86713.6 5016 230124.0 96806 20249.庆7 0 0 70 四218624. 7075 464763.5 17899.59383川03 6 2 12 贵42214.1 2768 16495.62415.21 13507州 4 3 01 云135897. 6267 348426.0 16086 18575. 南97 9 4 1 62 西30406.7 462971.0 16195.6023 12963藏 3 3 56 陕48692.1 5707 154529.1 12950 18245. 西7 7 9 5 23 —30949.0 3128 14988.56684.68 1740肃0 0 68 青15603.1 -J 638.43 8741 9851.28 2659海31 /宁49509.8 1219 17578.23149.90 620夏 6 6 92 新28993.1 4045 15513.52280.36 46519疆 1 1 62 数据来源：1.中国统计年鉴2012，2.中国旅游年鉴2012。

X X X学院实验报告第 1 页（1）用eviews得到数据如下：建立回归模型：AHE=-6.631562+0.186713*CLFPRM+0.004974*UNRMR2=0.622402，F=11.53822，P=0.001094，T=（-2.093464）（4.419819）（0.238515）可知城市男性劳动参与率和城市男性失业率与真实的平均小时工资存在正相关关系。

经济意义：说明在其他条件保持不变的情况下，城市男性劳动参与率每增加一个百分点，真实的平均小时工资增加0.186713美元，城市男性失业率每增加百分之一，真实的平均小时工资增加0.004974美元。

（2）用eviews得到数据如下：建立回归模型：AHE=10.60094-0.05345*CLFPRFR2=0.65384，F=28.33262，P=0.000085，T=（18.85195）（-5.32284）可知城市女性劳动参与率与真实的平均小时工资存在负相关关系。

经济意义：说明在其他条件保持不变的情况下，城市女性劳动参与率每增加一个百分点，真实的平均小时工资减少0.05345美元。

（3）用eviews得到数据如下：第 3 页建立回归模型：AHE=157.048-1.919573*CLFPRM-0.232917*UNRMR2=0.91981，F=80.29262，P=0.000，T=（11.69701）（-10.72079）（-2.635153）可知城市男性劳动参与率和城市男性失业率与当前平均小时工资存在显著的负相关关系。

经济意义：说明在其他条件保持不变的情况下，城市男性劳动参与率每增加百分之一，当前平均小时工资减少1.919573美元，城市男性失业率每增加百分之一，当前平均小时工资减少0.232917美元。

（4）用eviews得到数据如下：建立回归模型：AHE=-23.92719+0.595155*CLFPRFR2=0.958337，F=345.0332，P=0.000，T=（-13.33538）（18.57507）可知城市女性劳动参与率与当前平均小时工资存在显著的正相关关系。

多元线性回归模型实验报告计量经济学Revised by BLUE on the afternoon of December 12,2020.实验报告课程名称金融计量学实验项目名称多元线性回归模型班级与班级代码实验室名称（或课室）专业任课教师xxx学号： xxx姓名： xxx 实验日期： 2012年 5 月3日广东商学院教务处制姓名 xxx 实验报告成绩评语：指导教师（签名）年月日说明：指导教师评分后，实验报告交院（系）办公室保存多元线性回归模型一、实验目的通过上机实验,使学生能够使用 Eviews 软件估计可化为线性回归模型的非线性模型，并对线性回归模型的参数线性约束条件进行检验。

二、实验内容（一）根据中国某年按行业分的全部制造业国有企业及规模以上制造业非国有企业的工业总产值Y，资产合计K及职工人数L进行回归分析。

（二）掌握可化为线性多元非线性回归模型的估计和多元线性回归模型的线性约束条件的检验方法（三）根据实验结果判断中国该年制造业总体的规模报酬状态如何三、实验步骤（一）收集数据下表列示出来中国某年按行业分的全部制造业国有企业及规模以上制造业非国有企业的工业总产值Y，资产合计K及职工人数L。

序号工业总产值Y（亿元）资产合计K（亿元）职工人数L（万人）序号工业总产值Y（亿元）资产合计K（亿元）职工人数L（万人）1 113 17 432 67 18 613 84 19 2404 27 20 2225 327 21 806 120 22 967 58 23 2228 31 24 1639 16 25 24410 66 26 14511 58 27 13812 28 28 4613 61 29 21814 254 30 1915 83 31 4516 33表1（二）创建工作文件（Workfile）。

1、启动Eviews5，在主菜单上依次点击File\New\Workfile（如图），按确定。

2、在弹出的对话框中选择数据的时间频率（本实验为序列数据），输入数据数为31（如图1），然后点击OK（如图2）。

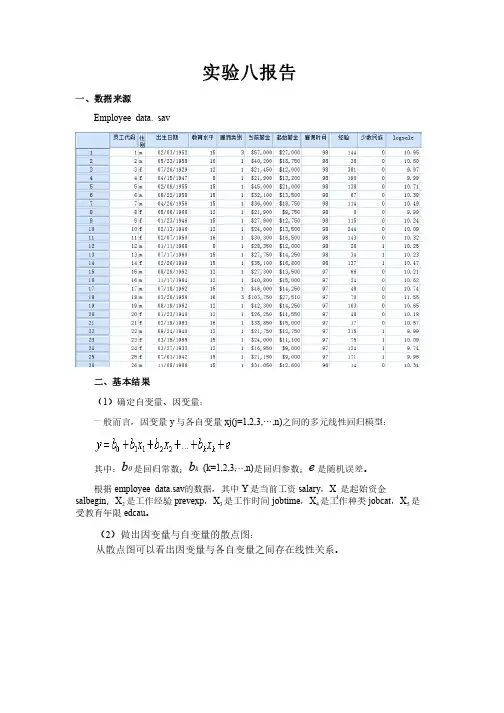
实验八报告一、数据来源Employee data. sav 二、基本结果（1）确定自变量、因变量：）确定自变量、因变量：一般而言，因变量y与各自变量xj(j=1,2,3,…,n)之间的多元线性回归模型：之间的多元线性回归模型：其中：b0是回归常数；b k (k=1,2,3,…,n)是回归参数；e是随机误差。

是随机误差。

根据employee data.sav的数据，其中Y是当前工资salary，X1是起始资金salbegin，X2是工作经验prevexp，X3是工作时间jobtime，X4是工作种类jobcat，X5是受教育年限edcau。

（2）做出因变量与自变量的散点图：）做出因变量与自变量的散点图：从散点图可以看出因变量与各自变量之间存在线性关系。

（3）检验因变量Y是否服从正态分布的模型假定——因变量Y并没有很好地服从正态分布。

地服从正态分布。

的残差图（4）线性回归Y的残差图此标准化残差图表明，此线性回归的标准化残差呈楔形分布而非带状分布，不满足回归模型同方差的假定。

布，不满足回归模型同方差的假定。

当前薪金多元线性回归分析的残差图图当前薪金多元线性回归分析的残差图（5）通过以上检验可以看出，当前薪金并不是好的变量，对当前薪金进行Ln变换（取对数）生成新的随进变量logsale，将logsale作为因变量Y用逐步回归的方法进行回归分析：的方法进行回归分析：1）p-p图：图：较好的服从了正态分布。

发现取对数后，logY较好的服从了正态分布。

2）logY的标准化残差图：的标准化残差图：上图表明因变量Y（logsale）的标准化残差近似呈带状分布，满足模型同方差的假定。

差的假定。

3）逐步回归的判定系数：）逐步回归的判定系数：通过逐步回归，得到方程的判定系数如下表。

R²越接近1，说明回归方程解释了因变量总变异量的绝大部分比例。

本估计的回归方程有一个好的拟合，，可以认为拟合度高。

在模型5中达到0.810，且调整后的R²达到0.808，可以认为拟合度高。

《多元统计与程序设计》课程实验报告1 实验内容（1）掌握回归分析和逐步回归分析的思想和计算步骤；（2）用Matlab实现回归分析和逐步回归分析；2 模型建立与求解2.1回归分析2.1.1模型的建立设随机变量y与m个自变量存在线性关系：y= (2.1.1)式（2.1.1）称为回归方程，其中称为回归系数，为随机变量，称为随机误差，它可理解为y无法用表示的是其他各种随机因素造成的误差。

要用来估计随机变量y的均值E（y）,即E（y）=此处假定,y。

其中，，是与无关的待定系数。

设有n组样本观测值数据：其中表示第i次试验或第i个样本关于变量的观测值。

于是有：==………（2.1.2）其中，为m+1个待定系数，为n 个相互独立的且服从同一正态分布的随机变量，式（2.1.2）称为多元（m 元）线性回归数学模型。

式（2.1.2）也可写成矩阵形式，设⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=nm n n m m x x x x x xx x x X 212222111211111则式（2.1.2）可表示为（2.1.3）式（2.1.3）称为多元线性回归模型的矩阵形式。

2.1.2回归模型中参数的确定采用最小二乘法来对回归模型式（2.3）中的作最小二乘估计。

设m 3210，b，，b ，b ，b b 分别是的最小二乘估计值，于是有 m m 22110x b x b x b b yˆ++++=（2.1.4）式（2.1.4）中：yˆ是y 中的一个最小二乘估计。

对于每一个试验数据。

由式（2.1.4），可得一个i ˆy，即：n i x b x b b yim m i i ,,2,1ˆ110 =+++=，。

这里称i ˆy 为实际值i y 的回归值。

显然，回归值i yˆ与实际值i y 有误差，即 i y -i ˆy=n i x b x b b y im m i i ,,2,1110 =+++-， 当然我们希望i ˆy与i y 值偏离程度越小越好，这样才能使回归值i ˆy 与实际值i y 拟合得最好。

回归分析实验报告实验报告：回归分析摘要：回归分析是一种用于探究变量之间关系的数学模型。

本实验以地气温和电力消耗量数据为例，运用回归分析方法，建立了气温和电力消耗量之间的线性回归模型，并对模型进行了评估和预测。

实验结果表明，气温对电力消耗量具有显著的影响，模型能够很好地解释二者之间的关系。

1.引言回归分析是一种用于探究变量之间关系的统计方法，它通常用于预测或解释一个变量因另一个或多个变量而变化的程度。

回归分析陶冶于20世纪初，经过不断的发展和完善，成为了数量宏大且复杂的数据分析的重要工具。

本实验旨在通过回归分析方法，探究气温与电力消耗量之间的关系，并基于建立的线性回归模型进行预测。

2.实验设计与数据收集本实验选择地的气温和电力消耗量作为研究对象，数据选取了一段时间内每天的气温和对应的电力消耗量。

数据的收集方法包括了实地观测和数据记录，并在数据整理过程中进行了数据的筛选与清洗。

3.数据分析与模型建立为了探究气温与电力消耗量之间的关系，需要建立一个合适的数学模型。

根据回归分析的基本原理，我们初步假设气温与电力消耗量之间的关系是线性的。

因此，我们选用了简单线性回归模型进行分析，并通过最小二乘法对模型进行了估计。

运用统计软件对数据进行处理，并进行了以下分析：1)描述性统计分析：计算了气温和电力消耗量的平均值、标准差和相关系数等。

2)直线拟合与评估：运用最小二乘法拟合出了气温对电力消耗量的线性回归模型，并进行了模型的评估，包括了相关系数、残差分析等。

3)预测分析：基于建立的模型，进行了其中一未来日期的电力消耗量的预测，并给出了预测结果的置信区间。

4.结果与讨论根据实验数据的分析结果，我们得到了以下结论：1)在地的气温与电力消耗量之间存在着显著的线性关系，相关系数为0.75，表明二者之间的关系较为紧密。

2)构建的线性回归模型：电力消耗量=2.5+0.3*气温，模型参数的显著性检验结果为t=3.2，p<0.05，表明回归系数是显著的。

试验汇报课程名称金融计量学试验项目名称多元线性回归模型班级与班级代码试验室名称（或课室）专业任课老师xxx学号: xxx姓名: xxx试验日期: 5 月3日广东商学院教务处制姓名xxx 试验汇报成绩评语:指导老师（署名）年月日说明: 指导老师评分后, 试验汇报交院（系）办公室保留多元线性回归模型一、试验目经过上机试验,使学生能够使用 Eviews 软件估量可化为线性回归模型非线性模型, 并对线性回归模型参数线性约束条件进行检验。

二、试验内容（一）依据中国某年按行业分全部制造业国有企业及规模以上制造业非国有企业工业总产值Y, 资产累计K及职员人数L进行回归分析。

（二）掌握可化为线性多元非线性回归模型估量和多元线性回归模型线性约束条件检验方法（三）依据试验结果判定中国该年制造业总体规模酬劳状态怎样？三、试验步骤（一）搜集数据下表列示出来中国某年按行业分全部制造业国有企业及规模以上制造业非国有企业工业总产值Y, 资产累计K及职员人数L。

序号工业总产值Y（亿元）资产累计K（亿元）职员人数L（万人）序号工业总产值Y（亿元）资产累计K（亿元）职员人数L（万人）1 3722.7 3078.22 113 17 812.7 1118.81 432 1442.52 1684.43 67 18 1899.7 2052.16 613 1752.37 2742.77 84 19 3692.85 6113.11 2404 1451.29 1973.82 27 20 4732.9 9228.25 2225 5149.3 5917.01 327 21 2180.23 2866.65 806 2291.16 1758.77 120 22 2539.76 2545.63 967 1345.17 939.1 58 23 3046.95 4787.9 2228 656.77 694.94 31 24 2192.63 3255.29 1639 370.18 363.48 16 25 5364.83 8129.68 24410 1590.36 2511.99 66 26 4834.68 5260.2 14511 616.71 973.73 58 27 7549.58 7518.79 13812 617.94 516.01 28 28 867.91 984.52 4613 4429.19 3785.91 61 29 4611.39 18626.94 21814 5749.02 8688.03 254 30 170.3 610.91 1915 1781.37 2798.9 83 31 325.53 1523.19 4516 1243.07 1808.44 33表1（二）创建工作文件（Workfile）。

多元统计分析实验报告（精选多篇）第一篇：多元统计分析实验报告多元统计分析得实验报告院系:数学系班级:1３级 B 班姓名:陈翔学号:2013１611233 实验目得:比较三大行业得优劣性实验过程有如下得内容:(１)正态性检验;(2)主体间因子,多变量检验a;(３)主体间效应得检验;(4)对比结果(K 矩阵);(5)多变量检验结果;(６)单变量检验结果;(7)协方差矩阵等同性得Box 检验ａ,误差方差等同性得Ｌevene 检验 a;(8)估计;(9)成对比较,多变量检验;(10)单变量检验。

实验结果:综上所述,我们对三个行业得运营能力进行了具体得比较分析,所得数据表明,从总体来瞧,信息技术业要稍好于电力、煤气及水得生产与供应业以及房地产业。

１。

正态性检验Kｏlmogorｏv－SｍirnovaShapiｒ o—Wilk 统计量 dｆ Sig.统计量ｄｆ Sig、净资产收益率。

１１３ 35、2００＊。

97８ 35。

6７7 总资产报酬率。

121 35、２00＊。

964 3５、298 资产负债率。

08６ 35。

2００*.9６2 35、265 总资产周转率.1８0 3５、006。

864 ３5。

00０流动资产周转率、164 3５、０18.88５35、002 已获利息倍数、２8１35.０00。

55１３5、0０0 销售增长率.1０3 ３５、2０0＊。

９4９ 35、104 资本积累率。

251 35。

０00、655 35。

0０0 *。

这就是真实显著水平得下限。

ａ。

Lillｉeforｓ显著水平修正此表给出了对每一个变量进行正态性检验得结果,因为该例中样本中ｎ＝35<2000,所以此处选用 Shapiro—W ｉｌk 统计量。

由 Sig。

值可以瞧到,总资产周转率、流动资产周转率、已获利息倍数及资本积累率均明显不遵从正态分布,因此,在下面得分析中,我们只对净资产收益率、总资产报酬率、资产负债率及销售增长率这四个指标进行比较,并认为这四个变量组成得向量遵从正态分布(尽管事实上并非如此)。

回归分析实验报告回归分析实验报告引言：回归分析是一种常用的统计方法，用于探究变量之间的关系。

本实验旨在通过回归分析来研究某一自变量对因变量的影响，并进一步预测未来的趋势。

通过实验数据的收集和分析，我们可以得出一些有关变量之间关系的结论，并为决策提供依据。

数据收集：在本次实验中，我们收集了一组数据，包括自变量X和因变量Y的取值。

为了保证数据的可靠性和准确性，我们采用了随机抽样的方法，并对数据进行了严格的统计处理。

数据分析：首先，我们进行了数据的可视化分析，绘制了散点图以观察变量之间的分布情况。

通过观察散点图，我们可以初步判断变量之间是否存在线性关系。

接下来，我们使用回归分析方法对数据进行了拟合，并得到了回归方程。

回归方程：通过回归分析，我们得到了如下的回归方程：Y = a + bX其中，a表示截距，b表示斜率。

回归方程可以用来预测因变量Y在给定自变量X的取值时的期望值。

回归系数的解释：在回归方程中，截距a表示当自变量X为0时，因变量Y的取值。

斜率b表示自变量X每变动一个单位时，因变量Y的平均变动量。

通过对回归系数的解释，我们可以更好地理解变量之间的关系。

回归方程的显著性检验：为了验证回归方程的有效性，我们进行了显著性检验。

通过计算回归方程的F值和P值，我们可以判断回归方程是否具有统计学意义。

如果P值小于显著性水平（通常为0.05），则我们可以拒绝零假设，即回归方程是显著的。

回归方程的拟合优度：为了评估回归方程的拟合程度，我们计算了拟合优度（R²）。

拟合优度表示因变量的变异程度可以被自变量解释的比例。

拟合优度的取值范围为0~1，值越接近1表示回归方程对数据的拟合程度越好。

回归方程的预测：通过回归方程，我们可以进行因变量Y的预测。

当给定自变量X的取值时，我们可以利用回归方程计算出因变量Y的期望值。

预测结果可以为决策提供参考，并帮助我们了解自变量对因变量的影响程度。

结论：通过本次实验，我们成功地应用了回归分析方法，研究了自变量X对因变量Y的影响，并得到了回归方程。

多元线性回归实例分析报告多元线性回归是一种用于预测目标变量和多个自变量之间关系的统计分析方法。

它可以帮助我们理解多个自变量对目标变量的影响，并通过建立回归模型进行预测。

本文将以一个实例为例，详细介绍多元线性回归的分析步骤和结果。

假设我们研究了一个电子产品公司的销售数据，并想通过多元线性回归来预测销售额。

我们收集了以下数据：目标变量（销售额）和三个自变量（广告费用、产品种类和市场规模）。

首先，我们需要对数据进行探索性分析，了解数据的分布、缺失值等情况。

我们可以使用散点图和相关系数矩阵来查看变量之间的关系。

通过绘制广告费用与销售额的散点图，我们可以观察到一定的正相关关系。

相关系数矩阵可以用来度量变量之间的线性关系的强度和方向。

接下来，我们需要构建多元线性回归模型。

假设目标变量（销售额）与三个自变量（广告费用、产品种类和市场规模）之间存在线性关系，模型可以表示为：销售额=β0+β1*广告费用+β2*产品种类+β3*市场规模+ε其中，β0是截距，β1、β2和β3是回归系数，ε是误差项。

我们可以使用最小二乘法估计回归系数。

最小二乘法可以最小化目标变量的预测值和实际值之间的差异的平方和。

通过计算最小二乘估计得到的回归系数，我们可以建立多元线性回归模型。

在实际应用中，我们通常使用统计软件来进行多元线性回归分析。

通过输入相应的数据和设置模型参数，软件会自动计算回归系数和其他统计指标。

例如，我们可以使用Python的statsmodels库或R语言的lm函数来进行多元线性回归分析。

最后，我们需要评估回归模型的拟合程度和预测能力。

常见的评估指标包括R方值和调整R方值。

R方值可以描述自变量对因变量的解释程度，值越接近1表示拟合程度越好。

调整R方值考虑了模型中自变量的个数，避免了过度拟合的问题。

在我们的实例中，假设我们得到了一个R方值为0.8的多元线性回归模型，说明模型可以解释目标变量80%的方差。

这个模型还可以用来进行销售额的预测。

回归分析实验报告实验报告实验课程：[信息分析]专业：[信息管理与信息系统]班级：[ ]学⽣姓名：[ ]指导教师：[请输⼊姓名]完成时间：2013年6⽉28⽇⼀．实验⽬的多元线性回归简单地说是涉及多个⾃变量的回归分析，主要功能是处理两个变量之间的线性关系，建⽴线性数学模型并进⾏评价预测。

本实验要求掌握附带残差分析的多元线性回归理论与⽅法。

⼆．实验环境实验室308教室三．实验步骤与内容1打开应⽤统计学实验指导书，新建excel表2．打开SPSS，将数据输⼊。

3．调⽤SPSS主菜单的分析——>回归——>线性命令，打开线性回归对话框，指定因变量（⼯业GDP⽐重）和⾃变量（⼯业劳动者⽐重、固定资产⽐重、定额资⾦流动⽐重），以及回归⽅式；逐步回归（图1）图1 线性对话框4.在统计栏中，选择估计以输出回归系数B的估计值、t统计量等，选择Duribin-watson以进⾏DW检验；选择模型拟合度输出拟合优度统计量值，如R^2、F统计量值等（图2）。

图2 统计量栏5．在线性回归栏中选择直⽅图和正态概率图以绘制标准化残差的直⽅图和残差分析与正态概率⽐较图，以标准化预测值为纵坐标，标准化残差值为横坐标，绘制残差与Y的预测值的散点图，检验误差变量的⽅差是否为常数（图3）。

图3 绘制栏6.提交分析，并在输出窗⼝中查看结果，以及对结果进⾏分析。

系统在进⾏逐步分析的过程中产⽣了两个回归模型，模型1先将与因变量（销售收⼊）线性关系的⾃变量地区⼈⼝引⼊模型，建⽴他们之间的⼀元线性关系。

⽽后逐步引⼊其他变量，表1中模型2表明将⾃变量⼈均收⼊引⼊，建⽴⼆元线性回归模型，可见地区⼈⼝和⼈均收⼊对销售收⼊的影响同等重要。

从表2中给出了两个模型各⾃的R^2和调整后的R^2,第⼀个模型中的销售收⼊中有99%的变动可以⽤地区⼈⼝的变动解释，第⼆个模型中地区⼈⼝和⼈均收⼊的变动可以解释销售收⼊中99.9%的变动，显然第⼆个模型的拟合数据效果⽐较好⼀点。