圆的切线的判定性质和画法
- 格式:ppt
- 大小:668.00 KB
- 文档页数:10

2024年中考重点之圆的切线与切圆定理圆是几何学中非常重要的基本形状之一,而关于圆的切线和切圆定理是中考数学中的重点内容之一。
本文将详细介绍圆的切线以及切圆定理的概念和应用。
一、圆的切线1. 切线的定义在平面几何中,切线是一条与圆只有一个交点的直线。
2. 切线的性质(1)切线与半径的关系:切线与半径垂直相交。
(2)切线的方向:切线与半径的夹角为90度。
(3)切线的长度:从切点到圆心的部分是切线的长度。
二、切圆定理1. 切圆定理的表述在一个圆中,如果一条直线通过圆上的两个不同的点,并且这条直线的两端分别与圆相交,那么这条直线就被称为切线,并且它与圆的切点在同一条直径上。
2. 切圆定理的应用(1)切线与半径的关系:由切圆定理可知,切线与半径在切点处构成90度的夹角,因此可以利用这一性质求解有关圆的问题。
(2)求切线长度:利用切圆定理可以通过已知的半径长度和圆心和切点的距离求解切线的长度。
(3)求切点坐标:利用切圆定理可以通过已知的圆心坐标和切线方程求解切点的坐标。
三、例题解析题目:已知一个圆的半径为r,圆心的坐标为(h, k),直线y = mx + c(m ≠ 0)经过与圆的两个交点,求切线的方程。
解析:根据题目中已知条件,直线y = mx + c与圆相交于两个不同的点。
由于直线是切线,因此切线与直径垂直相交,并且切点在同一条直径上。
设切点的坐标为(x1, y1),则根据切圆定理,切点的横坐标为h - (km + c)/(m^2 + 1),纵坐标为k + m(x1 - h)。
由于切线垂直于半径,可以得到切线的斜率为-1/m。
由切点坐标可以确定切线的方程为y - y1 = -(1/m)(x - x1)。
将切点的坐标代入切线方程,可以得到切线的具体方程为y - (k + m(x1 - h)) = -(1/m)(x - (h - (km + c)/(m^2 + 1)))。
至此,我们得到了关于切线的方程。
四、总结本文详细介绍了圆的切线和切圆定理的概念和应用。

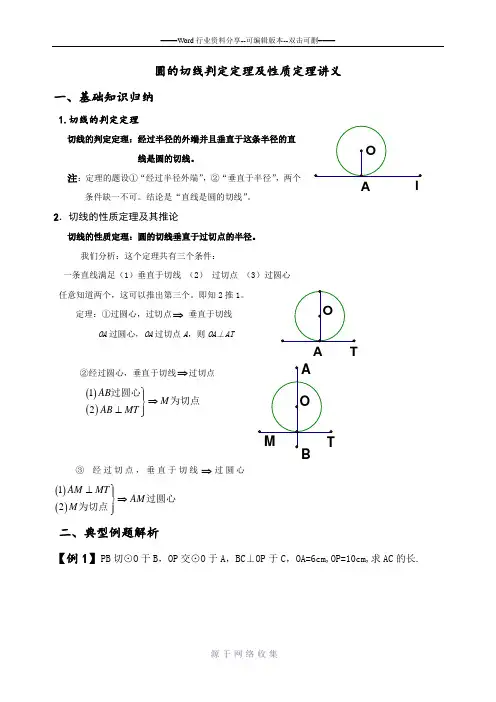
AT圆的切线判定定理及性质定理讲义一、基础知识归纳1.切线的判定定理切线的判定定理:经过半径的外端并且垂直于这条半径的直 线是圆的切线。
注:定理的题设①“经过半径外端”,②“垂直于半径”,两个 条件缺一不可。
结论是“直线是圆的切线”。
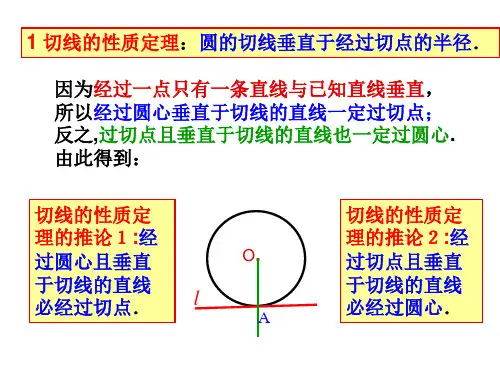
2.切线的性质定理及其推论切线的性质定理:圆的切线垂直于过切点的半径。
我们分析:这个定理共有三个条件:一条直线满足(1)垂直于切线 (2) 过切点 (3)过圆心 任意知道两个,这可以推出第三个。
即知2推1。
定理:①过圆心,过切点⇒ 垂直于切线 OA 过圆心,OA 过切点A ,则OA ⊥AT②经过圆心,垂直于切线⇒过切点()()12AB M AB MT ⎫⎪⇒⎬⊥⎪⎭过圆心为切点③ 经过切点,垂直于切线⇒过圆心()()12AM MT AM M ⊥⎫⎪⇒⎬⎪⎭过圆心为切点二、典型例题解析【例1】PB 切⊙O 于B ,OP 交⊙O 于A ,BC ⊥OP 于C ,OA=6cm,OP=10cm,求AC 的长.AAOBPCM【例2】如图,⊙O 的直径AB =6cm ,点P 是AB 延长线上的动点,过点P 作⊙O 的切线,切点为C ,连结AC .若CPA 的平分线交AC 于点M ,你认为∠CMP 的大 小是否发生变化?若变化,请说明理由;若不变,求出∠CMP 的度数【例3】如图,若⊙的直径AB 与弦AC 的夹角为30°,切线CD 与AB 的延长线交于点D,且⊙O 的半径为2,则CD 的长是多少?【例4】如图,AB 为半圆O 的直径,CB 是半圆O 的切线,B 是切点,AC•交半圆O 于点D ,已知CD=1,AD=3,那么cos ∠CAB=________.【例5】设直线ι到⊙O 的圆心的距离为d ,半径为R ,并使x 2-2d x +R=0,BDC试由关于x 的一元二次方程根的情况讨论ι与⊙O 的位置关系.【例6】在Rt ABC △中,90ACB ∠=°,D 是AB 边上一点,以BD 为直径的O ⊙与边AC 相切于点E ,连结DE 并延长,与BC 的延长线交于点F . (1)求证:BD BF =;(2)若64BC AD ==,,求O ⊙的面积.。


圆的切线:切线的定义、性质和求解方法切线是与圆相切于一点且只与圆的该点相交一次的直线。
切线与半径垂直,也就是与半径所在的直径形成直角。
切线的定义给定一个圆,如果通过圆上的一点作两条直线,其中一条与半径垂直且只与该点相交一次,那么称这条直线为这个圆的一条切线。
切线的性质1. 切线与圆相切于一点,且只与圆的该点相交一次。
2. 切线与半径垂直,即与半径所在的直径形成直角。
3. 以切点为端点的切线被称为切线段。
4. 圆心到切点的线段被称为切线的斜率。
切线的求解方法求解圆的切线可以根据以下步骤进行:1. 给定一个圆和切点P,连接圆心O与切点P,得到半径OP。
2. 利用切线性质,使切线与半径OP垂直,得到直角三角形。
3. 根据已知条件,计算切线的长度。
切线的长度可以通过利用勾股定理或几何构造法进行计算。
勾股定理法求切线长度1. 已知圆的半径r和切点与圆心的连线OP的长度d。
2. 根据勾股定理,有切线长度s的平方等于d的平方减去圆的半径r的平方,即s^2 = d^2 - r^2。
3. 取根号可以得到切线的长度s。
几何构造法求切线长度1. 已知圆的半径r和切点与圆心的连线OP的长度d。
2. 以切点为圆心,作一条半径为r的圆。
3. 连接圆心与新圆上与切点P相对应的点Q,得到直角三角形OPQ。
4. 根据直角三角形OPQ中的三边关系,可以计算出切线的长度s。
这是圆的切线的定义、性质和求解方法的简要介绍。
掌握这些基本概念和求解方法,可以帮助我们更好地理解和应用切线在几何学中的重要性。

九年级数学圆的切线的知识点数学中的圆是一个常见的几何图形,它有许多有趣的性质,其中之一就是切线。
切线是一个与圆相切于一点且与圆没有其它的交点的直线。
在这篇文章中,我们将探讨九年级数学课程中关于圆的切线的知识点。
1. 切线定义及性质切线是一个特殊的直线,它与圆只有一个交点,且与圆在该点的切线相切。
切线的性质有以下几点:(1) 切线与半径垂直:切线与从切点到圆心的半径垂直相交。
(2) 弦切角相等:切线和过切点的弦所夹的角相等。
(3) 切线长度相等:从圆外的任意一点引切线,得到的切线长度都相等。
2. 切线的判定方法在几何中,判断一条直线是否为圆的切线,有以下两种判定方法:(1) 切线判定法一:若直线与圆只有一个交点,并且该交点到圆心的距离等于圆的半径,则该直线是圆的切线。
(2) 切线判定法二:若直线与圆相交,且与圆的切点处平分被切角,那么该直线也是圆的切线。
3. 切线的性质在解题中的应用切线的性质经常在解题过程中被使用,下面介绍几个常见的应用情况:(1) 切线的长度:我们可以利用切线的性质来求解切线的长度。
根据切线与半径垂直的性质,我们可以使用勾股定理或者勾股定理的变形来求解切线的长度。
(2) 弦的长度:通过切线和弦的切角相等的性质,我们可以利用已知的切线长度和弦的长度来计算未知的切线或者弦的长度。
(3) 切线的方程:切线与圆的关系可以通过方程来表示。
我们可以利用切线判定法一中的条件,得到切线方程的一般形式。
4. 实际生活中的切线应用切线在实际生活中有许多应用,下面介绍几个例子:(1) 轮胎的设计:车辆的轮胎通常是圆形的,轮胎的切线对于保证行驶的稳定性非常重要。
(2) 光学反射:光线在两种介质之间传播时,若入射角等于反射角,则光线与界面的交点所在的直线即为切线。
(3) 经济决策:在经济学中,曲线图表上的切线可以表示某一点的边际效应,帮助决策者做出合理的判断。
总结起来,九年级数学课程中关于圆的切线的知识点包括切线的定义及性质,切线的判定方法,切线性质的应用,以及实际生活中的切线应用。

圆切线的性质及判定一.切线的判定方法:⑴.切线的定义:与圆有唯一公共点的直线叫做圆的切线。
⑵.到圆心的距离等于半径的直线是圆的切线⑶.经过半径的外端,并且垂直于这条半径的直线是圆的切线。
二.辅助线规律:(1)直线与圆有公共点时,辅助线的作法是“连结圆心和公共点”,再证直线与半径垂直简称:“有点,连接,证垂直”。
即当条件中已知直线与圆有公共点时,利用“⑶.经过半径的外端,并且垂直于这条半径的直线是圆的切线”证明。
(2)当直线与圆并没明确有公共点时,辅助线的作法是“过圆心向直线作垂线”,再证圆心到直线的距离等于半径简称:“无点,作垂线,证(等于)半径”。
即当条件没有告诉直线与圆有公共点时,利用“(2)到圆心的距离等于半径的直线是圆的切线;”证明。
三.例题讲析:例1. 已知:直线AB经过⊙O上的点C,并且OA=OB,CA=CB求证:直线AB是⊙O的切线。
例2. 如图,已知OA=OB=5厘米,AB=8厘米,⊙O的直径为6厘米求证:AB与⊙O相切例3. 如图,已知AB是⊙O的直径,点D在AB的延长线上,BD=OB,点C在圆上,∠CAB=30°.求证:DC是⊙O的切线。
例4. 如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D.求证:AC平分∠DAB。
例5. 已知:AB是⊙O的直径,BC是⊙O的切线,切点为B,OC平行于AD求证:DC是⊙O的切线。
例6. 如图,A是⊙O外一点,连OA交⊙O于C,过⊙O上一点P作OA的垂线交OA于F,交⊙O于E,连结PA,若∠FPC=∠CPA.求证:PA是⊙O的切线例7. 如图,AB=AC,以AB为直径的⊙O交BC于D,DE⊥AC于E求证:DE与⊙O相切例8. 如图,已知AB为⊙O的直径,BC切⊙O于B,AC交⊙O于P,CE=EB,E点在BC上。
求证:PE是⊙O的切线。
四.练习:1、如图7,AB为⊙O直径,PA、PC为⊙O的切线,A、C为切点,∠BAC=30°(1)求∠P大小。
切线的判定1.切线的性质:垂直于过切点的半径.(连半径,得垂直)l2.切线的判定:(1)定义法:和圆只有一个交点的直线是圆的切线;(2)距离法:到圆心距离等于半径的直线是圆的切线;l证明d=r即可,常用于已知数据的计算,比如动圆相切问题.(3)判定定理:经过半径外端且垂直于这条半径的直线是圆的切线.换个说法:⎧⎨⎩有交点:连半径,证垂直无交点:作垂直,证半径,多用于几何证明.多为有交点,重点考虑如何证垂直:①证明和已知垂线平行;②证明夹角为直角.3.常见相切图(1)角分+等腰得平行:点C在以AB为直径的圆O上,AH⊥CH,且AC平分∠HAB.连接OC,则OC=OA,∴∠OCA=∠OAC,又∠OAC=∠HAC,∴∠OCA=∠HAC,∴OC∥AH,∴OC⊥CH,∴CH是圆O的切线.(2)证明和已知直角相等.证明△PCO≌△P AO,可得∠PCO=∠P AO=90°.B(3)证明夹角为直角.(弦切角定理)如图,若∠BAC=∠D,则AB是圆O切线.B如图,连接AO并延长交圆O于点P,则∠P=∠D=∠BAC,∵∠P+∠P AC=90°,∴∠BAC+∠P AC=90°,即AB⊥AP,∴AB是圆O的切线.B1.(2018·滨州)如图,AB 为O 的直径,点C 在O 上,AD CD ⊥于点D ,且AC 平分DAB ∠,求证:(1)直线DC 是O 的切线;(2)22AC AD AO =⋅.【分析】(1)连接OC ,∵OA =OC ,∴∠OAC =∠OCA ,又AC 平分∠DAB ,∴∠DAC =∠OAC , ∴∠OCA =∠DAC ,∴AD ∥OC , ∵AD ⊥CD ,∴OC ⊥CD , ∴DC 是圆O 的切线.(2)连接BC ,过点C 作CH ⊥AN 交AB 于H 点,则2AC AH AB =⋅,∵AH =AD ,AB =2AO , ∴22AC AD AO =⋅.2.(2018·泰州)如图,AB 为O 的直径,C 为O 上一点,ABC ∠的平分线交O 于点D ,DE BC ⊥于点E .(1)试判断DE 与O 的位置关系,并说明理由;(2)过点D 作DF AB ⊥于点F,若BE =3DF =,求图中阴影部分的面积.B【分析】 (1)相切.连接OD ,∵BD 平分∠ABE ,∴∠ABD =∠EBD , ∵OB =OD ,∴∠OBD =∠ODB , ∴∠EBD =∠ODB ,∴OD ∥BE , ∵DE ⊥BE ,∴OD ⊥DE , ∴DE 与圆O 相切.(2)易证△BED ≌△BFD,∴BF =BE =DF =3,∴∠ABD =30°,连接OD ,则∠AOD =60°,易证OD =∴(2113262S ππ=⋅-=, 故阴影部分面积为2π-.【角分+等腰得平行】3.(2018·锦州)如图,在ABC∆中,90C∠=︒,AE平分BAC∠交BC于点E,O是AB 上一点,经过A,E两点的O交AB于点D,连接DE,作DEA∠的平分线EF交O 于点F,连接AF.(1)求证:BC是O的切线.(2)若4sin5EFA∠=,AF=AC的长.【分析】(1)连接EO,则OA=OE,∴∠OAE=∠OEA,又AE平分∠BAC,∴∠OAE=∠CAE,∴∠OEA=∠CAE,∴OE∥AC,∵AC⊥BC,∴OE⊥BC,∴BC是圆O的切线.(2)EF平分∠AED,则点F是半圆AD中点,连接OF,则△AOF是等腰直角三角形,∴5OA AF===,∴AD=10,4sin sin5EDA EFA∠=∠=,∴AE=8,DE=6,∵AE平分∠BAC,∴4 cos cos5CAE EAD∠=∠=,即45ACAE=,∴44328555AC AE==⨯=,故AC的长为325.4.(2018·毕节市)如图,在△ABC中,以BC为直径的圆C交AC于点E,过点E作AB的垂线交AB于点F,交CB的延长线于点G,且∠ABG=2∠C.(1)求证:EG是圆O的切线;(2)若1tan2C=,AC=8,求圆O的半径.【分析】(1)连接OE,则OE=OC,∴∠OEC=∠OCE,∴∠EOG=2∠C,又∠ABG=2∠C,∴∠EOG=∠ABG,∴OE∥AB,∵EG⊥AB,∴EG⊥OE,∴EG是圆O的切线.(2)连接BE,则BE⊥AC,∵OE∥AB,∴△ABC是等腰三角形,∴E是AC中点,∵AC=8,∴142CE AC==,∵1tan2C=,∴122BE CE==,∴BC=r=OB,故圆O.【有交点,证垂直,全等证明夹角为直角】5.(2019·天水)如图,AB、AC分别是O的直径和弦,OD AC⊥于点D.过点A作O 的切线与OD的延长线交于点P,PC、AB的延长线交于点F.(1)求证:PC是O的切线;(2)若60ABC∠=︒,10AB=,求线段CF的长.【分析】(1)连接OC,∵OP⊥AC,∴OP平分AC,∴OP是AC的垂直平分线,∴P A=PC,易证△POA≌△POC,∴∠PCO=∠P AO=90°,∴OC⊥PC,∴PC是圆O的切线.(2)若∠ABC=60°则△OBC是等边三角形,∴∠BOC=60°,OC=OB=5,在Rt△OCF中,CF=故CF的长为6.(2016·郴州)如图,OA ,OD 是O 半径,过A 作O 的切线,交AOD ∠的平分线于点C ,连接CD ,延长AO 交O 于点E ,交CD 的延长线于点B (1)求证:直线CD 是O 的切线;(2)如果D 点是BC 的中点,O 的半径为3cm ,求DE 的长度(结果保留)πB【分析】(1)易证△COA ≌△COD ,∴∠ODC =∠OAC =90°,即OD ⊥CD ,∴CD 是圆O 的切线.(2)若点D 是BC 的中点,则△BOC 是等腰三角形,∴∠OBC =∠OCB ,又∠OCB =∠OCA ,∴设∠OBC =∠OCB =∠OCA =α, ∴390α=︒,30α=︒,∴∠BOD =60°,∴1236DE ππ=⋅⋅=cm ,故DE 的长度是πcm .7.(2018·丹东)如图,直线AD 经过O 上的点A ,ABC ∆为O 的内接三角形,并且CAD B ∠=∠.(1)判断直线AD 与O 的位置关系,并说明理由;(2)若30CAD ∠=︒,O 的半径为1,求图中阴影部分的面积.(结果保留)πD【分析】 (1)相切.连接AO 并延长交圆O 于点P ,连接CP ,则∠P =∠B ,又∵∠B =∠CAD ,∴∠P =∠CAD , ∵∠P +∠P AC =90°,∴∠CAD +∠P AC =90°, ∴P A ⊥AD ,∴AD 是圆O 的切线.(2)连接OC ,则∠AOC =2∠APC =2∠CAD =60°,21166S ππ=⋅⋅=扇AOC,21AOCS=∴6S π=阴,故阴影部分的面积为6π-【有交点证垂直,证明夹角为直角】8.(2019·盐城)如图,在Rt△ABC中,90ACB∠=︒,CD是斜边AB上的中线,以CD为直径的O分别交AC、BC于点M、N,过点N作NE AB⊥,垂足为E.(1)若O的半径为52,6AC=,求BN的长;(2)求证:NE与O相切.【分析】(1)∵52r=,∴CD=5,∴AB=10,∴BC=8,连接DN,则DN⊥BC,∴DN∥AC,∴点N是BC中点,∴118422BN BC==⨯=.故BN的长为4.(2)连接NO,∵N、O分别是BC、CD中点,∴NO∥BD,∵NE⊥BD,∴NE⊥NO,∴NE与圆O相切.9.(2018·本溪)如图,在Rt△ABC中,∠C=90°,点O,D分别为AB,BC的中点,连接OD,作⊙O与AC相切于点E,在AC边上取一点F,使DF=DO,连接DF.(1)判断直线DF与⊙O的位置关系,并说明理由;(2)当∠A=30°,CF时,求⊙O的半径.【分析】(1)相切.连接OE,则OE⊥AC,∴点E是AC边中点,连接OF,过点O作OH⊥DF交DF于H点,∵DO∥AC,∴∠DOF=∠OF A,又DO=DF,∴∠DOF=∠DFO,∴∠OF A=∠OFD,易证△OFE≌△OFH,∴OH=OE,∴DF是圆O的切线.(2)设半径为r,则CD=r,DF=DO,∴CF=,又CF,∴r=1,10.(2018·江西)如图,在△ABC 中,O 为AC 上一点,以点O 为圆心,OC 为半径做圆,与BC 相切于点C ,过点A 作AD ⊥BO 交BO 的延长线于点D ,且∠AOD =∠BAD . (1)求证:AB 为⊙O 的切线; (2)若BC =6,tan ∠ABC =43,求AD 的长.【分析】(1)∵∠AOD +∠DAO =90°,∠ABD +∠BAD =90°,且∠AOD =∠BAD ,∴∠DAO =∠ABD ,又∠DAO =∠OBC , ∴∠ABD =∠OBC ,过点O 作OH ⊥AB 交AB 于H 点,易证△BOH ≌△BOC ,∴OH =OC ,∴AB 是圆O 的切线. (2)∵BC =6,4tan 3ABC ∠=,∴AC =8,AB =10, BH =BC =6,AH =4,OH =3,OA =5,∴5OD ===2AD OD ==.故AD 的长为【圆中等腰三角形】11.(2018·鄂尔多斯)如图,O 是ABC ∆的外接圆,AC 是直径,弦BD BA =,EB DC ⊥,交DC 的延长线于点E . (1)求证:BE 是O 的切线; (2)当3sin 4BCE ∠=,3AB =时,求AD 的长.【分析】(1)连接BO 并延长,分别交AD 、圆O 于点H 、Q ,易证△BDQ ≌△BAQ ,∴DQ =AQ ,又AB =DB , ∴BQ 是AD 的垂直平分线, ∴BQ ⊥AD ,∵AC 是直径,∴∠ADC =90°,又∠E =90°,∴AD ∥BE , ∴BQ ⊥BE ,∴BE 是圆O 的切线.(2)∵∠BAC =∠CBE ,∴∠ACB =∠BCE ,∴3sin 4ACB ∠=,∵AB=3,∴AC =4,BC∵3sin 4BE BCE BC ∠===,∴BE =, ∴HD BE ==,∴AD =2HD .故AD。

圆的切线与切点的性质与判定圆是几何学中的重要概念之一,它有很多特性和性质。
其中一个重要的性质是切线与切点的关系。
本文将介绍切线与切点的性质以及判定方法。
一、切线与切点的定义在几何学中,我们定义一个几何图形与另一个图形的一点相切时,这个点是该图形的切点,而与该图形相切的直线称为切线。
对于圆来说,切点是与圆相交于一点的直线,这条直线同时也是圆的切线。
二、切线与切点的性质1. 切点与圆心连线垂直于切线假设有一个圆,它的圆心是O,切点是A,切线是l。
根据性质,可以得出结论:切点与圆心连线AO垂直于切线l。
这一性质可以通过几何推理或使用垂直性质证明得出。
2. 切线与半径的夹角切线与半径的夹角等于90度。
对于任意一条半径OA和切线l,我们可以推导出∠OAL=90°。
这个性质也可以通过几何证明得出。
3. 切点在切线上的唯一性每条切线与圆只有一个切点。
这个切点是在圆上与切线相切的点,其他点不与切线相切。
也就是说,对于一条切线l和圆O,它们的切点A是唯一的。
4. 切线在切点处切分弦切线在切点处将切点外的弦分为两段,其中一个是切点外的弧。
三、切点的判定方法如何判断一条直线是否是圆的切线?下面是两种判定方法:1. 切线定理给定一个圆,如果一个直线与圆相交,在交点处的切角为90度,则这条直线是圆的切线。
换句话说,如果一个线段与圆相交于一点,并与半径的延长线构成90度的夹角,那么这条线段就是圆的切线。
2. 切线的斜率圆的切线的斜率与切点处圆的切线相切。
通过计算待判定的直线与给定圆的相切点的斜率,如果该斜率等于切点切线的斜率,那么这条直线就是圆的切线。
四、实际应用切线和切点的性质在几何学和物理学中有广泛的应用。
例如,在求解圆的切线问题时,可以利用切点与圆心连线垂直于切线的性质,来确定切线方程的斜率。
在实际生活中,切线和切点的性质也用于计算机图形学、光学等领域,例如,用于光线的反射和折射的计算。
总结:本文介绍了圆的切线与切点的性质与判定方法。

圆的切线知识点总结
圆的切线知识点总结
圆的切线定理知识包括了切线长定理、切割线定理和割线定理。
圆的切线
垂直于过切点的半径;经过半径的`一端,并且垂直于这条半径的直线,是这个圆的切线。
切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线。
切线的性质:(1)经过切点垂直于过切点的半径的直线是圆的切线。
(2)经过切点垂直于切线的直线必经过圆心。
(3)圆的切线垂直于经过切点的半径。
切线长定理:从圆外一点到圆的两条切线的长相等,那点与圆心的连线平分切线的夹角。
切割线定理:圆的一条切线与一条割线相交于p点,切线交圆于C点,割线交圆于A B两点,则有pC^2=pA·pB
割线定理:与切割线定理相似两条割线交于p点,割线m交圆于A1 B1两点,割线n交圆于A2 B2两点
则pA1·pB1=pA2·pB2。
初中数学知识归纳圆的切线与切点的性质初中数学知识归纳——圆的切线与切点的性质圆是初中数学中一个重要的图形,圆的切线和切点是圆的重要性质之一。
在本文中,我们将归纳总结初中数学中关于圆的切线与切点的性质。
一、圆的切线的定义与性质切线是与圆只有一个公共点的直线。
下面给出几个关于圆的切线的性质:1. 切线与半径垂直:一个切线与通过切点的半径垂直相交。
2. 切线长度相等:如果两条切线都与同一条半径垂直,则这两条切线的长度相等。
3. 外切线:若直线与圆外切,并且与通过切点的圆的半径垂直,则该直线是圆的外切线。
4. 内切线:若直线与圆内切,并且与通过切点的圆的半径垂直,则该直线是圆的内切线。
二、圆的切点的定义与性质切点是切线与圆的唯一交点。
下面给出几个关于圆的切点的性质:1. 切点在切线上:切点是切线与圆的唯一交点,所以切点一定在切线上。
2. 切点与半径的关系:切点与圆心连线构成的半径与切线垂直相交于切点。
3. 同一切线的切点关系:如果两条切线是同一直线的不同部分,那么它们在切点出重合。
三、切线与切点的应用圆的切线与切点的性质在几何证明和问题求解中有着广泛的应用。
下面以一个例题来说明:例题:已知圆 O 的半径为 5cm,过圆外一点 A 作圆的切线 AB,AB 的长度为 12cm,求 AB 与 OA 的夹角。
解析:根据圆的切线与半径垂直的性质可知,AO 与 AB 垂直相交于切点 B。
由于圆 O 的半径为 5cm,所以 OB = 5cm。
根据勾股定理,可得 AO² = AB² + OB²,即 OA² = 12² + 5²。
计算可得OA ≈ 13cm。
根据余弦定理,夹角 AOB 的余弦为cosθ = AB / OA,即 c osθ = 12 / 13。
通过反余弦函数可计算得到夹角 AOB 的近似值,约为 36.87°。
通过以上例题,我们可以看到切线与切点的性质在解决具体问题时非常有用。
三圆的切线的性质及判定定理[对应学生用书P25]1.切线的性质(1)性质定理:圆的切线垂直于经过切点的半径. 如图,已知AB 切⊙O 于A 点,则OA ⊥AB .(2)推论1:经过圆心且垂直于切线的直线必经过切点. (3)推论2:经过切点且垂直于切线的直线必经过圆心. 2.圆的切线的判定方法(1)定义:和圆只有一个公共点的直线是圆的切线. (2)数量关系:到圆心距离等于半径的直线是圆的切线. (3)定理:过半径外端点且与这条半径垂直的直线是圆的切线.其中(2)和(3)是由(1)推出的,(2)是用数量关系来判定,而(3)是用位置关系加以判定的.[说明] 在切线的判定定理中要分清定理的题设和结论,“经过半径的外端”和“垂直于这条半径”这两个条件缺一不可,否则该直线就不是圆的切线.[对应学生用书P25]圆的切线的性质[例1] 如图,已知∠C =90°,点O 在AC 上,CD 为⊙O 的直径,⊙O 切AB于E ,若BC =5,AC =12.求⊙O 的半径.[思路点拨] ⊙O 切AB 于点E ,由圆的切线的性质,易联想到连接OE 构造Rt △OAE ,再利用相似三角形的性质,求出⊙O 的半径.[解] 连接OE ,∵AB 与⊙O 切于点E , ∴OE ⊥AB ,即∠OEA =90°. ∵∠C =90°,∠A =∠A , ∴Rt △ACB ∽Rt △AEO , ∴OE BC =AOAB. ∵BC =5,AC =12,∴AB =13, ∴OE 5=12-OE 13,∴OE =103.即⊙O 的半径为103.利用圆的切线的性质来证明或进行有关的计算有时需添加辅助线,其中连接圆心和切点的半径是常用辅助线,从而可以构造直角三角形,利用直角三角形边角关系求解,或利用勾股定理求解,或利用三角形相似求解等.1.如图,AB 切⊙O 于点B ,延长AO 交⊙O 于点C ,连接BC .若∠A =40°,则∠C =( )A .20°B .25°C .40°D .50°解析:连接OB ,因为AB 切⊙O 于点B ,所以OB ⊥AB ,即∠ABO =90°,所以∠AOB =50°.又因为点C 在AO 的延长线上,且在⊙O 上, 所以∠C =12∠AOB =25°.答案:B2.如图,已知P AB 是⊙O 的割线,AB 为⊙O 的直径.PC 为⊙O 的切线,C 为切点,BD ⊥PC 于点D ,交⊙O 于点E ,P A =AO =OB =1.(1)求∠P 的度数; (2)求DE 的长. 解:(1)连接OC .∵C 为切点,∴OC ⊥PC ,△POC 为直角三角形. ∵OC =OA =1,PO =P A +AO =2, ∴sin ∠P =OC PO =12.∴∠P =30°.(2)∵BD ⊥PD ,∴在Rt △PBD 中, 由∠P =30°,PB =P A +AO +OB =3, 得BD =32.连接AE .则∠AEB =90°,∴AE ∥PD . ∴∠EAB =∠P =30°,∴BE =AB sin 30°=1,∴DE =BD -BE =12.圆的切线的判定[例2] 已知D 是△ABC ADB =60°,求证:AB 是△BCD 的外接圆的切线.[思路点拨]连接OB ,OC ,OD →∠BOD =90°→ ∠OBC =∠OCB =30°→∠ABO =90°→结论. [证明] 如图,连接OB ,OC ,OD ,OD 交BC 于E . ∵∠DCB 是BD 所对的圆周角, ∠BOD 是BD 所对的圆心角,∠BCD =45°, ∴∠BOD =90°.∵∠ADB 是△BCD 的一个外角, ∴∠DBC =∠ADB -∠ACB =60°-45°=15°, ∴∠DOC =2∠DBC =30°, 从而∠BOC =120°,∵OB =OC ,∴∠OBC =∠OCB =30°. 在△OEC 中,因为∠EOC =∠ECO =30°, ∴OE =EC ,在△BOE 中,因为∠BOE =90°,∠EBO =30°. ∴BE =2OE =2EC , ∴CE BE =CD DA =12, ∴AB ∥OD ,∴∠ABO =90°, 故AB 是△BCD 的外接圆的切线.要证明某直线是圆的切线,主要是运用切线的判定定理,除此以外,还有圆心到直线的距离等于半径等判定方法,但有时需添加辅助线构造判定条件,其中过圆心作直线的垂线是常用辅助线.3.本例中,若将已知改为“∠ABD =∠C ”,怎样证明:AB 是△BCD 的外接圆的切线. 证明:作直径BE ,连接DE , ∵BE 是⊙O 的直径,∴∠BDE =90°, ∴∠E +∠DBE =90°. ∵∠C =∠E ,∠ABD =∠C , ∴∠ABD +∠DBE =90°. 即∠ABE =90°.∴AB 是△BCD 的外接圆的切线.4.如图,△ABC 内接于⊙O ,点D 在OC 的延长线上,sin B =12,∠D =30°.(1)求证:AD 是⊙O 的切线. (2)若AC =6,求AD 的长. 解:(1)证明:如图,连接OA , ∵sin B =12,∴∠B =30°,∵∠AOC =2∠B ,∴∠AOC =60°, ∵∠D =30°,∴∠OAD =180°-∠D -∠AOC =90°, ∴AD 是⊙O 的切线. (2)∵OA =OC ,∠AOC =60°,∴△AOC 是等边三角形,∴OA =AC =6, ∵∠OAD =90°,∠D =30°, ∴AD =3AO =6 3.圆的切线的性质和判定的综合考查[例3] 如图,AB 为⊙O 的直径,D 是BC 的中点,DE ⊥AC 交AC 的延长线于E ,⊙O 的切线BF 交AD 的延长线于点F .(1)求证:DE 是⊙O 的切线;(2)若DE =3,⊙O 的半径为5,求BF 的长. [思路点拨] (1)连接OD ,证明OD ⊥DE ; (2)作DG ⊥AB . [证明] (1)连接OD , ∵D 是BC 中点,∴∠1=∠2. ∵OA =OD ,∴∠2=∠3. ∴∠1=∠3. ∴OD ∥AE .∵DE ⊥AE ,∴DE ⊥OD ,即DE 是⊙O 的切线. (2)过D 作DG ⊥AB , ∵∠1=∠2,∴DG =DE =3. 在Rt △ODG 中,OG =52-32=4, ∴AG =4+5=9.∵DG ⊥AB ,FB ⊥AB ,∴DG ∥FB . ∴△ADG ∽△AFB . ∴DG BF =AG AB. ∴3BF =910.∴BF =103.对圆的切线的性质与判定的综合考查往往是热点,其解答思路常常是先证明某直线是圆的切线,再利用切线的性质来求解相关结果.5.如图,已知两个同心圆O ,大圆的直径AB 交小圆于C 、D ,大圆的弦EF 切小圆于C ,ED 交小圆于G ,若小圆的半径为2,EF =43,试求EG 的长.解:连接GC ,则GC ⊥ED . ∵EF 和小圆切于C , ∴EF ⊥CD ,EC =12EF =2 3.又CD =4,∴在Rt △ECD 中, 有ED =EC 2+CD 2 =(23)2+42=27.由射影定理可知EC 2=EG ·ED , ∴EG =EC 2ED =(23)227=677.6.如图,以Rt △ABC 直角边AC 上一点O 为圆心,OC 为半径的⊙O 与AC 的另一个交点为E ,D 为斜边AB 上一点且在⊙O 上,AD 2=AE ·AC .(1)证明:AB 是⊙O 的切线; (2)若DE ·OB =8,求⊙O 的半径. 解:(1)证明:连接OD ,CD ,∵AD 2=AE ·AC , ∴AD AE =ACAD.又∵∠DAE =∠DAC , ∴△DAE ∽△CAD ,∴∠ADE =∠ACD . ∵OD =OC ,∴∠ACD =∠ODC , 又∵CE 是⊙O 的直径,∴∠ODE +∠CDO =90°,∴∠ODA =90°, ∴AB 是⊙O 的切线. (2)∵AB ,BC 是⊙O 的切线,∴OB ⊥DC ,∴DE ∥OB ,∴∠CED =∠COB , ∵∠EDC =∠OCB ,∴△CDE ∽△BCO , ∴DE CO =CEBO,DE ·OB =2R 2=8, ∴⊙O 的半径为2.[对应学生用书P27]一、选择题1.下列说法:①与圆有公共点的直线是圆的切线;②垂直于圆的半径的直线是圆的切线;③与圆心的距离等于半径的直线是圆的切线;④过直径的端点,垂直于此直径的直线是圆的切线.其中正确的有( )A .①②B .②③C .③④D .①④答案:C2.如图,AB 是⊙O 的直径,BC 是⊙O 的切线,AC 交⊙O 于D .AB =6,BC =8,则BD 等于( )A .4B .4.8C .5.2D .6解析:∵AB 是⊙O 的直径,∴BD ⊥AC . ∵BC 是⊙O 的切线,∴AB ⊥BC . ∵AB =6,BC =8,∴AC =10. ∴BD =AB ·BCAC =4.8.答案:B3.如图,CD 切⊙O 于B ,CO 的延长线交⊙O 于A ,若∠C =36°,则∠ABD 的度数是( )A .72°B .63°C .54°D .36°解析:连接OB .∵CD 为⊙O 的切线,∴∠OBC =90°. ∵∠C =36°,∴∠BOC =54°. 又∵∠BOC =2∠A ,∴∠A =27°, ∴∠ABD =∠A +∠C =27°+36°=63°. 答案:B4.如图,在⊙O 中,AB 为直径,AD 为弦,过B 点的切线与AD 的延长线交于C ,若AD =DC ,则sin ∠ACO 等于( )A.1010 B.210 C.55D.24 解析:连接BD ,则BD ⊥AC .∵AD =DC ,∴BA =BC , ∴∠BCA =45°.∵BC 是⊙O 的切线,切点为B , ∴∠OBC =90°.∴sin ∠BCO =OB OC =OB 5OB =55,cos ∠BCO =BC OC =2OB 5OB =255.∴sin ∠ACO =sin(45°-∠BCO ) =sin 45°cos ∠BCO -cos 45°sin ∠BCO =22×255-22×55=1010. 答案:A 二、填空题5.如图,已知∠AOB =30°,M 为OB 边上一点,以M 为圆心、2为半径作⊙M .若点M 在OB 边上运动,则当OM =________时,⊙M 与OA 相切.解析:若⊙M 与OA 相切,则圆心M 到直线OA 的距离等于圆的半径2.过M作MN⊥OA于点N,则MN=2.在Rt△MON中,∵∠MON=30°,∴OM=2MN=2×2=4.答案:46.已知P A是圆O的切线,切点为A,P A=2,AC是圆O的直径,PC与圆O交于B点,PB=1.则圆O 的半径R=________.解析:AB=AP2-PB2= 3.由AB2=PB·BC,∴BC=3,Rt△ABC中,AC=AB2+BC2=2 3.∴R= 3.答案: 37.圆O的直径AB=6,C为圆周上一点,BC=3,过C作圆的切线l,过A作l的垂线AD,AD分别与直线l、圆交于点D、E,则∠DAC=________,DC=________.解析:连接OC,∵OC=OB,∴∠OCB=∠OBC.又∠DCA+∠ACO=90°,∠ACO+∠OCB=90°,∴∠DCA=∠OCB,∵OC=3,BC=3,∴△OCB是正三角形.∴∠OBC=60°,即∠DCA=60°.∴∠DAC=30°.在Rt△ACB中,AC=AB2-BC2=33,DC=AC sin 30°=32 3.答案:30°33 2三、解答题8.如图所示,D是⊙O的直径AB的延长线上一点,PD是⊙O的切线,P是切点,∠D=30 °.求证:P A=PD.证明:如图,连接OP,∵PD是⊙O的切线,P为切点.∴PO⊥PD.∵∠D=30°,∴∠POD=60°.又∵OA=OP,∴∠A=∠APO=30°.∴∠A=∠D.∴P A=PD.9.如图,已知在△ABC中,AB=AC,以AB为直径的⊙O交BC于D,过D点作⊙O的切线交AC于E.求证:(1)DE⊥AC;(2)BD2=CE·CA.证明:(1)连接OD,AD.∵DE是⊙O的切线,D为切点,∴OD⊥DE.∵AB是⊙O的直径,∴AD⊥BC.又AB=AC,∴BD=DC.∴OD∥AC.∴DE⊥AC.(2)∵AD⊥BC,DE⊥AC,∴△CDE∽△CAD.∴CDCA=CECD.∴CD2=CE·CA.∴BD=DC.∴BD2=CE·CA.10.如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AE⊥CD,垂足为E,DA平分∠BDE.(1)求证:AE是⊙O的切线;(2)若∠DBC=30°,DE=1 cm,求BD的长.解:(1)证明:连接OA.∵DA平分∠BDE,∴∠BDA=∠EDA.∵OA=OD,∴∠ODA=∠OAD.∴∠OAD=∠EDA.∴OA∥CE.∵AE⊥DE,∴∠AED=90°,∴∠OAE=∠DEA=90°.∴AE⊥OA.∴AE是⊙O的切线.(2)∵BD是直径,∴∠BCD=∠BAD=90°.∵∠DBC=30°,∴∠BDC=60°.∴∠BDE=120°.∵DA平分∠BDE,∴∠BDA=∠EDA=60°.∴∠ABD=∠EAD=30°.在Rt△AED中,∠AED=90°,∠EAD=30°,∴AD=2DE.在Rt△ABD中,∠BAD=90°,∠ABD=30°,∴BD=2AD=4DE.∵DE的长是1 cm,∴BD的长是4 cm.。
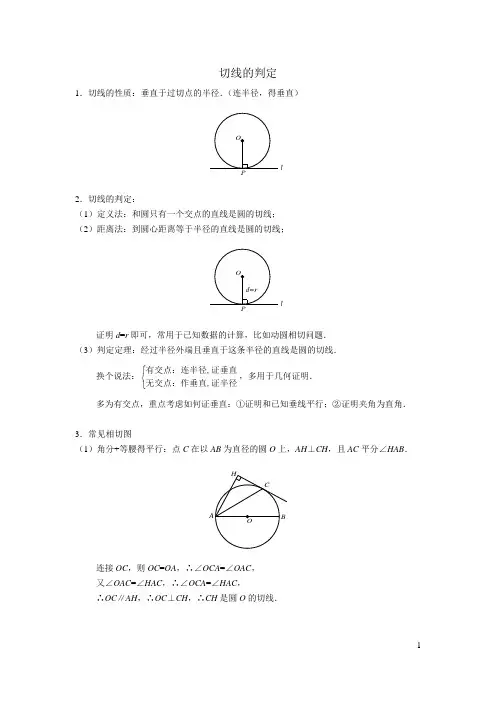
切线的判定方法
切线指的是一条刚好触碰到曲线上某一点的直线。
圆的切线的判定方法有:和圆只有一个公共点的直线是圆的切线;和圆心的距离等于圆的半径的直线是圆的切线;经过半径的外端并且垂直于这条半径的直线是圆的切线。
一、切线的性质定理
圆的切线垂直于经过切点的半径。
推论1:经过圆心且垂直于切线的直线必经过切点。
推论2:经过切点且垂直于切线的直线必经过圆心。
二、切线的主要性质
(1)切线和圆只有一个公共点;
(2)切线和圆心的距离等于圆的半径;
(3)切线垂直于经过切点的半径;
(4)经过圆心垂直于切线的直线必过切点;
(5)经过切点垂直于切线的直线必过圆心;
(6)从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项。