_圆的切线性质与判定定理
- 格式:ppt
- 大小:374.50 KB
- 文档页数:17



圆的切线判定和性质(教案)第一章:圆的切线定义和判定1.1 圆的切线定义引入圆的切线概念,讲解切线的定义和特点展示圆的切线示意图,让学生理解切线与圆的关系1.2 圆的切线判定条件讲解圆的切线的判定条件通过示例和练习,让学生掌握如何判断一条直线是否为圆的切线第二章:圆的切线性质2.1 圆的切线性质介绍圆的切线的性质,如切线与半径垂直、切线与圆心连线垂直等展示切线性质的示意图,让学生理解并记忆这些性质2.2 圆的切线定理讲解圆的切线定理,如切线定理、切线长定理等通过示例和练习,让学生掌握切线定理的应用和证明方法第三章:圆的切线方程3.1 圆的切线方程的定义和特点讲解圆的切线方程的定义和特点展示切线方程的示意图,让学生理解切线方程的形式和含义3.2 圆的切线方程的求法讲解如何求解圆的切线方程通过示例和练习,让学生掌握求解切线方程的方法和技巧第四章:圆的切线与圆的位置关系4.1 圆的切线与圆相切讲解圆的切线与圆相切的情况和特点展示切线与圆相切的示意图,让学生理解切线与圆的切点、切线与半径的关系4.2 圆的切线与圆相离讲解圆的切线与圆相离的情况和特点通过示例和练习,让学生掌握如何判断切线与圆的位置关系第五章:圆的切线应用5.1 圆的切线与圆的切点应用讲解如何利用切点性质解决问题,如求解切线长度、切线与半径的关系等通过示例和练习,让学生掌握切点性质的应用方法5.2 圆的切线与圆的方程应用讲解如何利用切线方程解决问题,如求解切线方程、判断切线与圆的位置关系等通过示例和练习,让学生掌握切线方程的应用方法第六章:圆的切线与圆的交点应用6.1 圆的切线与圆的交点性质讲解圆的切线与圆的交点的性质,如切线与圆的交点与圆心连线垂直、交点到圆心的距离等于半径等展示切线与圆的交点性质的示意图,让学生理解并记忆这些性质6.2 圆的切线与圆的交点应用讲解如何利用切线与圆的交点解决问题,如求解交点坐标、判断交点与圆的关系等通过示例和练习,让学生掌握切线与圆的交点的应用方法第七章:圆的切线与圆的切线应用7.1 圆的切线与圆的切线相交讲解圆的切线与圆的切线相交的情况和特点展示切线与切线相交的示意图,让学生理解切线与切线的交点、切线与半径的关系7.2 圆的切线与圆的切线平行讲解圆的切线与圆的切线平行的情况和特点通过示例和练习,让学生掌握如何判断切线与切线的位置关系第八章:圆的切线与圆的切线综合应用8.1 圆的切线与圆的切线相切讲解圆的切线与圆的切线相切的情况和特点展示切线与切线相切的示意图,让学生理解切线与切线的切点、切线与半径的关系8.2 圆的切线与圆的切线综合应用讲解如何利用切线与切线综合解决问题,如求解切线与切线的交点、判断切线与圆的位置关系等通过示例和练习,让学生掌握切线与切线综合的应用方法第九章:圆的切线与圆的应用实例9.1 圆的切线与圆的切割应用实例讲解圆的切线与圆的切割应用实例,如切割线段、切割角度等展示切割应用实例的示意图,让学生理解切割原理和应用9.2 圆的切线与圆的轨迹应用实例讲解圆的切线与圆的轨迹应用实例,如轨迹方程、轨迹图形等通过示例和练习,让学生掌握切线与圆的轨迹的应用方法第十章:圆的切线综合练习10.1 圆的切线综合练习题提供一系列圆的切线综合练习题,让学生巩固所学知识通过解答练习题,让学生提高解题能力和综合运用能力10.2 圆的切线综合练习解答提供练习题的解答和解析,帮助学生理解和掌握解题方法通过练习解答,让学生巩固知识,提高学习效果重点和难点解析一、圆的切线定义和判定(第一章)重点关注内容:圆的切线的定义和特点,以及如何判断一条直线是否为圆的切线。

1与切线有关的定理一、切线的性质及判定 1. 切线的性质:定理:圆的切线垂直于过切点的半径.推论1:经过圆心且垂直于切线的直线必经过切点. 推论2:经过切点且垂直于切线的直线必经过圆心. 2. 切线的判定:定义法:和圆只有一个公共点的直线是圆的切线; 距离法:到圆心距离等于半径的直线是圆的切线;定理:经过半径的外端并且垂直于这条半径的直线是圆的切线. 3. 切线长和切线长定理:⑴ 切线长:在经过圆外一点的圆的切线上,这点和切点之间的线段的长,叫做这点到圆的切线长.⑵ 切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角.①切线的判定定理设OA 为⊙O 的半径,过半径外端A 作l ⊥OA ,则O 到l 的距离d=r ,∴l 与⊙O 相切.因此,我们得到:切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线. 注:定理的题设①“经过半径外端”,②“垂直于半径”,两个条件缺一不可.结论是“直线是圆的切线”.举例说明:只满足题设的一个条件不是⊙O 的切线.l AlAl证明一直线是圆的切线有两个思路:(1)连接半径,证直线与此半径垂直;(2)作垂线,证垂足在圆上②切线的性质定理及其推论切线的性质定理:圆的切线垂直于过切点的半径. 二、内切圆1. 定义:和三角形各边都相切的圆叫做三角形的内切圆,内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.P22. 多边形内切圆:和多边形的各边都相切的圆叫做多边形的内切圆,这个多边形叫做圆的外切多边形.3.直角三角形的内切圆半径与三边关系OF ED C BACBA CBAcbacba(1) (2)图(1)中,设a b c ,,分别为ABC ∆中A B C ∠∠∠,,的对边,面积为S 则内切圆半径(1)s r p=,其中()12pa b c =++;图(2)中,90C∠=︒,则()12r a b c =+-cm,BC=14 cm ,CA=13 cm ,求AF 、BD 、CE 的长例2. 如图所示,已知:AB是⊙O的直径,BC是⊙O的切线,切点为B。

圆的切线的性质及判定定理圆的相切的定义:直线和圆只有一个公共点,即圆心到直线的距离等于半径,这条直线叫圆的切线。
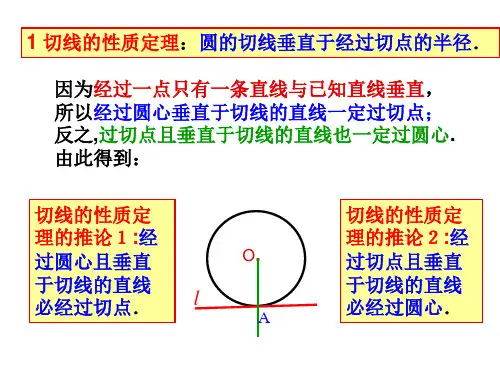
切线的性质定理:圆的切线垂直于经过切点的半径。
推论1:经过圆心且垂直于切线的直线必经过切点;推论2:经过切点且垂直于切线的直线必经过圆心。
切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线。
直线与圆的位置关系:相离:直线和圆没有公共点,即圆心到直线的距离大于半径;相交:直线和圆有两个公共点,即圆心到直线的距离小于半径,这条直线叫圆的割线;相切:直线和圆只有一个公共点,即圆心到直线的距离等于半径,这条直线叫圆的切线。
圆内接四边形的性质与判定定理圆内接四边形的概念:如果一个多边形的所有顶点都在一个圆上,这个多边形就叫做圆内接多边形,这个圆就是多边形的外接圆。
圆内接四边形的性质:圆内接四边形对角互补;圆内接四边形的外角等于它的内角的对角。
圆内接四边形的判定:如果一个四边形的对角互补,那么这个四边形的四个顶点共圆。
推论:如果一个四边形的一个外角等于它的内角的对角,那么这个四边形的四个顶点共圆。
方法总结:1、在解决与圆内接四边形有关的问题时,要注意观察图形,分清四边形的外角和内对角的位置,正确应用性质.2、当两圆相交时,常常通过连结两圆的公共弦,构建出圆内接四边形,进一步解决问题.圆周角定理圆周角的定义:顶点在圆上,它们的两边在圆内的部分分别是圆的弦•一条弧所对的圆周角等于它所对的圆心角的一半。
圆心角定理:圆心角的度数等于它所对弧的度数。
推论1:同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧也相推论2:半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径。
圆周角的特点:(1) 角的顶点在圆上;(2) 角的两边在圆内的部分是圆的弦.圆周角和圆心角相对于圆心与直径的位置关系有三种:A A A解题规律:解决圆周角和圆心角的计算和证明问题,要准确找出同弧所对的圆周角和圆心角,然后再灵活运用圆周角定理.。

圆的切线知识点总结一、切线的定义在欧式几何中,对圆的切线有以下几种定义:1. 如果一条直线与圆相交于两点,那么这条直线就被称为圆的切线。
2. 一条直线与圆相交于圆上的一点,那么这条直线就是圆的切线。
3. 一条直线与圆相切于圆上的一点,且直线上的其他点都在圆的外部,那么这条直线就是圆的切线。
这三种定义表达了切线与圆的位置关系,指出了切线与圆的相交情况以及位置特征。
二、切线的性质1. 切线与半径垂直圆的半径与切线的交点处相互垂直。
2. 切线定理若直线l与圆相切于点P,直线l与直径所夹的角为直角。
3. 切线长度相等过圆外一点作一切线与圆相交于A、B两点,连接线A、B,若CA=CB,则线段CA与线段CB构成圆的切线。
4. 切线的判定若直线l经过圆外一点,分别与圆上两点A、B相连,若线段AB的中点恰好是圆心O,那么直线l即为圆的切线。
5. 切线的唯一性圆外一点到圆的切线唯一。
以上是切线的主要性质,这些性质在解题时常常起到重要的作用,特别是在证明几何问题时,能够帮助我们理解和应用切线的知识。
三、切线与圆的位置关系1. 内切线如果一条直线与圆相交于圆上的一点,但直线上的其他点都在圆的内部,那么这条直线就是圆的内切线。
2. 外切线如果一条直线与圆相交于圆上的一点,且直线上的其他点都在圆的外部,那么这条直线就是圆的外切线。
3. 相切线如果一条直线与圆相切于圆上的一点,且直线上的其他点都在圆的外部,那么这条直线就是圆的相切线。
切线与圆的位置关系在解题时十分重要,通过分析切线和圆的位置关系,可以帮助我们求解许多几何问题。
四、切线的判定方法1. 切线与圆的位置关系我们可以通过切线与圆的位置关系来判断一条直线是否为圆的切线,如切线的定义所述,可以分析直线与圆的相交情况以及位置特征来判定切线。
2. 对于圆外一点到圆的切线的判定,我们可以利用中位线作图,利用几何思维判定出直线是否为圆的切线。
3. 切线定理的应用切线定理是判定切线的重要原理之一,通过利用切线定理,可以判定一条直线是否为圆的切线。




圆的切线判定定理
圆的切线判定定理是一个用于判断一条直线是否为圆的切线的准则。
根据该定理,当一条直线与圆相切时,该直线与圆的切点之间的线段与圆的半径垂直。
具体来说,如果一条直线与圆相交,且通过与圆的切点,与圆的半径垂直相交,那么这条直线就是圆的切线。
换句话说,这条直线切到了圆的边界,只与圆相交于切点。
这个定理可以用一个简单的几何证明来解释。
假设有一个圆和一条直线,直线通过圆的切点,并且与圆的半径垂直相交。
我们可以证明这条直线是圆的切线,因为根据几何定理,直线与圆的边界只能相交于两个点,而这两个点中的一个就是切点。
因此,这条直线与圆的边界只有一个交点,这就是切点,所以这条直线是圆的切线。
总之,圆的切线判定定理告诉我们,当一条直线与圆相交,且通过切点与圆的半径垂直相交时,这条直线就是圆的切线。
圆的十八个定理圆的十八个定理包括:1.圆心角定理:在同圆或等圆中,相等的圆心角所对弧相等,所对的弦相等,所对的弦的弦心距相等。
2.圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半。
3.垂径定理:垂直弦的直径平分该弦,并且平分这条弦所对的两条弧。
4.切线之判定定理:经过半径的外端并且垂直于该半径的直线是圆的切线。
5.切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,这一点与圆心的连线平分这两条切线的夹角。
6.公切线长定理:如果两圆有两条外公切线或两条内公切线,那么这两条外公切线长相等,两条内公切线长也相等。
如果他们相交,那么交点一定在两圆的连心线上。
7.相交弦定理:圆内两条弦相交,被交点分成的两条线段长的乘积相等。
8.切割线定理:从圆外一点向圆引一条切线和一条割线,则切线长是这点到割线与圆的两个交点的两条线段长的比例中项。
9.割线长定理:从圆外一点向圆引两条割线,这一点到每条割线与圆的交点的两条线段长的积相等。
10.切线的性质定理:圆的切线垂直于经过切点的半径。
11.弦切角定理:弦切角等于它所夹的弧对的圆周角。
12.定理:相交两圆的连心线垂直平分两圆的公共弦。
13.把圆分成n(n≥3)个等分:依次连结各分点所得的多边形是这个圆的内接正n边形;经过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正n边形。
14.任何正多边形都有一个外接圆和一个内切圆,这两个圆是同心圆。
15.正n边形的半径和边心距把正n边形分成2n个全等的直角三角形。
16.圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角。
17.两圆的半径分别为R、r,圆心距为d:两圆外离d>R+r;两圆外切d=R+r;两圆相交R-r<dr);两圆内切d=R-r(R>r);两圆内含d<R-r(R>r)。
18.圆锥曲线:圆是一种特殊的圆锥曲线,它是由一个固定点(焦点)和一个固定直线(准线)上的所有点的轨迹组成的。
三圆的切线的性质及判定定理[对应学生用书P25]1.切线的性质(1)性质定理:圆的切线垂直于经过切点的半径. 如图,已知AB 切⊙O 于A 点,则OA ⊥AB .(2)推论1:经过圆心且垂直于切线的直线必经过切点. (3)推论2:经过切点且垂直于切线的直线必经过圆心. 2.圆的切线的判定方法(1)定义:和圆只有一个公共点的直线是圆的切线. (2)数量关系:到圆心距离等于半径的直线是圆的切线. (3)定理:过半径外端点且与这条半径垂直的直线是圆的切线.其中(2)和(3)是由(1)推出的,(2)是用数量关系来判定,而(3)是用位置关系加以判定的.[说明] 在切线的判定定理中要分清定理的题设和结论,“经过半径的外端”和“垂直于这条半径”这两个条件缺一不可,否则该直线就不是圆的切线.[对应学生用书P25]圆的切线的性质[例1] 如图,已知∠C =90°,点O 在AC 上,CD 为⊙O 的直径,⊙O 切AB于E ,若BC =5,AC =12.求⊙O 的半径.[思路点拨] ⊙O 切AB 于点E ,由圆的切线的性质,易联想到连接OE 构造Rt △OAE ,再利用相似三角形的性质,求出⊙O 的半径.[解] 连接OE ,∵AB 与⊙O 切于点E , ∴OE ⊥AB ,即∠OEA =90°. ∵∠C =90°,∠A =∠A , ∴Rt △ACB ∽Rt △AEO , ∴OE BC =AOAB. ∵BC =5,AC =12,∴AB =13, ∴OE 5=12-OE 13,∴OE =103.即⊙O 的半径为103.利用圆的切线的性质来证明或进行有关的计算有时需添加辅助线,其中连接圆心和切点的半径是常用辅助线,从而可以构造直角三角形,利用直角三角形边角关系求解,或利用勾股定理求解,或利用三角形相似求解等.1.如图,AB 切⊙O 于点B ,延长AO 交⊙O 于点C ,连接BC .若∠A =40°,则∠C =( )A .20°B .25°C .40°D .50°解析:连接OB ,因为AB 切⊙O 于点B ,所以OB ⊥AB ,即∠ABO =90°,所以∠AOB =50°.又因为点C 在AO 的延长线上,且在⊙O 上, 所以∠C =12∠AOB =25°.答案:B2.如图,已知P AB 是⊙O 的割线,AB 为⊙O 的直径.PC 为⊙O 的切线,C 为切点,BD ⊥PC 于点D ,交⊙O 于点E ,P A =AO =OB =1.(1)求∠P 的度数; (2)求DE 的长. 解:(1)连接OC .∵C 为切点,∴OC ⊥PC ,△POC 为直角三角形. ∵OC =OA =1,PO =P A +AO =2, ∴sin ∠P =OC PO =12.∴∠P =30°.(2)∵BD ⊥PD ,∴在Rt △PBD 中, 由∠P =30°,PB =P A +AO +OB =3, 得BD =32.连接AE .则∠AEB =90°,∴AE ∥PD . ∴∠EAB =∠P =30°,∴BE =AB sin 30°=1,∴DE =BD -BE =12.圆的切线的判定[例2] 已知D 是△ABC ADB =60°,求证:AB 是△BCD 的外接圆的切线.[思路点拨]连接OB ,OC ,OD →∠BOD =90°→ ∠OBC =∠OCB =30°→∠ABO =90°→结论. [证明] 如图,连接OB ,OC ,OD ,OD 交BC 于E . ∵∠DCB 是BD 所对的圆周角, ∠BOD 是BD 所对的圆心角,∠BCD =45°, ∴∠BOD =90°.∵∠ADB 是△BCD 的一个外角, ∴∠DBC =∠ADB -∠ACB =60°-45°=15°, ∴∠DOC =2∠DBC =30°, 从而∠BOC =120°,∵OB =OC ,∴∠OBC =∠OCB =30°. 在△OEC 中,因为∠EOC =∠ECO =30°, ∴OE =EC ,在△BOE 中,因为∠BOE =90°,∠EBO =30°. ∴BE =2OE =2EC , ∴CE BE =CD DA =12, ∴AB ∥OD ,∴∠ABO =90°, 故AB 是△BCD 的外接圆的切线.要证明某直线是圆的切线,主要是运用切线的判定定理,除此以外,还有圆心到直线的距离等于半径等判定方法,但有时需添加辅助线构造判定条件,其中过圆心作直线的垂线是常用辅助线.3.本例中,若将已知改为“∠ABD =∠C ”,怎样证明:AB 是△BCD 的外接圆的切线. 证明:作直径BE ,连接DE , ∵BE 是⊙O 的直径,∴∠BDE =90°, ∴∠E +∠DBE =90°. ∵∠C =∠E ,∠ABD =∠C , ∴∠ABD +∠DBE =90°. 即∠ABE =90°.∴AB 是△BCD 的外接圆的切线.4.如图,△ABC 内接于⊙O ,点D 在OC 的延长线上,sin B =12,∠D =30°.(1)求证:AD 是⊙O 的切线. (2)若AC =6,求AD 的长. 解:(1)证明:如图,连接OA , ∵sin B =12,∴∠B =30°,∵∠AOC =2∠B ,∴∠AOC =60°, ∵∠D =30°,∴∠OAD =180°-∠D -∠AOC =90°, ∴AD 是⊙O 的切线. (2)∵OA =OC ,∠AOC =60°,∴△AOC 是等边三角形,∴OA =AC =6, ∵∠OAD =90°,∠D =30°, ∴AD =3AO =6 3.圆的切线的性质和判定的综合考查[例3] 如图,AB 为⊙O 的直径,D 是BC 的中点,DE ⊥AC 交AC 的延长线于E ,⊙O 的切线BF 交AD 的延长线于点F .(1)求证:DE 是⊙O 的切线;(2)若DE =3,⊙O 的半径为5,求BF 的长. [思路点拨] (1)连接OD ,证明OD ⊥DE ; (2)作DG ⊥AB . [证明] (1)连接OD , ∵D 是BC 中点,∴∠1=∠2. ∵OA =OD ,∴∠2=∠3. ∴∠1=∠3. ∴OD ∥AE .∵DE ⊥AE ,∴DE ⊥OD ,即DE 是⊙O 的切线. (2)过D 作DG ⊥AB , ∵∠1=∠2,∴DG =DE =3. 在Rt △ODG 中,OG =52-32=4, ∴AG =4+5=9.∵DG ⊥AB ,FB ⊥AB ,∴DG ∥FB . ∴△ADG ∽△AFB . ∴DG BF =AG AB. ∴3BF =910.∴BF =103.对圆的切线的性质与判定的综合考查往往是热点,其解答思路常常是先证明某直线是圆的切线,再利用切线的性质来求解相关结果.5.如图,已知两个同心圆O ,大圆的直径AB 交小圆于C 、D ,大圆的弦EF 切小圆于C ,ED 交小圆于G ,若小圆的半径为2,EF =43,试求EG 的长.解:连接GC ,则GC ⊥ED . ∵EF 和小圆切于C , ∴EF ⊥CD ,EC =12EF =2 3.又CD =4,∴在Rt △ECD 中, 有ED =EC 2+CD 2 =(23)2+42=27.由射影定理可知EC 2=EG ·ED , ∴EG =EC 2ED =(23)227=677.6.如图,以Rt △ABC 直角边AC 上一点O 为圆心,OC 为半径的⊙O 与AC 的另一个交点为E ,D 为斜边AB 上一点且在⊙O 上,AD 2=AE ·AC .(1)证明:AB 是⊙O 的切线; (2)若DE ·OB =8,求⊙O 的半径. 解:(1)证明:连接OD ,CD ,∵AD 2=AE ·AC , ∴AD AE =ACAD.又∵∠DAE =∠DAC , ∴△DAE ∽△CAD ,∴∠ADE =∠ACD . ∵OD =OC ,∴∠ACD =∠ODC , 又∵CE 是⊙O 的直径,∴∠ODE +∠CDO =90°,∴∠ODA =90°, ∴AB 是⊙O 的切线. (2)∵AB ,BC 是⊙O 的切线,∴OB ⊥DC ,∴DE ∥OB ,∴∠CED =∠COB , ∵∠EDC =∠OCB ,∴△CDE ∽△BCO , ∴DE CO =CEBO,DE ·OB =2R 2=8, ∴⊙O 的半径为2.[对应学生用书P27]一、选择题1.下列说法:①与圆有公共点的直线是圆的切线;②垂直于圆的半径的直线是圆的切线;③与圆心的距离等于半径的直线是圆的切线;④过直径的端点,垂直于此直径的直线是圆的切线.其中正确的有( )A .①②B .②③C .③④D .①④答案:C2.如图,AB 是⊙O 的直径,BC 是⊙O 的切线,AC 交⊙O 于D .AB =6,BC =8,则BD 等于( )A .4B .4.8C .5.2D .6解析:∵AB 是⊙O 的直径,∴BD ⊥AC . ∵BC 是⊙O 的切线,∴AB ⊥BC . ∵AB =6,BC =8,∴AC =10. ∴BD =AB ·BCAC =4.8.答案:B3.如图,CD 切⊙O 于B ,CO 的延长线交⊙O 于A ,若∠C =36°,则∠ABD 的度数是( )A .72°B .63°C .54°D .36°解析:连接OB .∵CD 为⊙O 的切线,∴∠OBC =90°. ∵∠C =36°,∴∠BOC =54°. 又∵∠BOC =2∠A ,∴∠A =27°, ∴∠ABD =∠A +∠C =27°+36°=63°. 答案:B4.如图,在⊙O 中,AB 为直径,AD 为弦,过B 点的切线与AD 的延长线交于C ,若AD =DC ,则sin ∠ACO 等于( )A.1010 B.210 C.55D.24 解析:连接BD ,则BD ⊥AC .∵AD =DC ,∴BA =BC , ∴∠BCA =45°.∵BC 是⊙O 的切线,切点为B , ∴∠OBC =90°.∴sin ∠BCO =OB OC =OB 5OB =55,cos ∠BCO =BC OC =2OB 5OB =255.∴sin ∠ACO =sin(45°-∠BCO ) =sin 45°cos ∠BCO -cos 45°sin ∠BCO =22×255-22×55=1010. 答案:A 二、填空题5.如图,已知∠AOB =30°,M 为OB 边上一点,以M 为圆心、2为半径作⊙M .若点M 在OB 边上运动,则当OM =________时,⊙M 与OA 相切.解析:若⊙M 与OA 相切,则圆心M 到直线OA 的距离等于圆的半径2.过M作MN⊥OA于点N,则MN=2.在Rt△MON中,∵∠MON=30°,∴OM=2MN=2×2=4.答案:46.已知P A是圆O的切线,切点为A,P A=2,AC是圆O的直径,PC与圆O交于B点,PB=1.则圆O 的半径R=________.解析:AB=AP2-PB2= 3.由AB2=PB·BC,∴BC=3,Rt△ABC中,AC=AB2+BC2=2 3.∴R= 3.答案: 37.圆O的直径AB=6,C为圆周上一点,BC=3,过C作圆的切线l,过A作l的垂线AD,AD分别与直线l、圆交于点D、E,则∠DAC=________,DC=________.解析:连接OC,∵OC=OB,∴∠OCB=∠OBC.又∠DCA+∠ACO=90°,∠ACO+∠OCB=90°,∴∠DCA=∠OCB,∵OC=3,BC=3,∴△OCB是正三角形.∴∠OBC=60°,即∠DCA=60°.∴∠DAC=30°.在Rt△ACB中,AC=AB2-BC2=33,DC=AC sin 30°=32 3.答案:30°33 2三、解答题8.如图所示,D是⊙O的直径AB的延长线上一点,PD是⊙O的切线,P是切点,∠D=30 °.求证:P A=PD.证明:如图,连接OP,∵PD是⊙O的切线,P为切点.∴PO⊥PD.∵∠D=30°,∴∠POD=60°.又∵OA=OP,∴∠A=∠APO=30°.∴∠A=∠D.∴P A=PD.9.如图,已知在△ABC中,AB=AC,以AB为直径的⊙O交BC于D,过D点作⊙O的切线交AC于E.求证:(1)DE⊥AC;(2)BD2=CE·CA.证明:(1)连接OD,AD.∵DE是⊙O的切线,D为切点,∴OD⊥DE.∵AB是⊙O的直径,∴AD⊥BC.又AB=AC,∴BD=DC.∴OD∥AC.∴DE⊥AC.(2)∵AD⊥BC,DE⊥AC,∴△CDE∽△CAD.∴CDCA=CECD.∴CD2=CE·CA.∴BD=DC.∴BD2=CE·CA.10.如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AE⊥CD,垂足为E,DA平分∠BDE.(1)求证:AE是⊙O的切线;(2)若∠DBC=30°,DE=1 cm,求BD的长.解:(1)证明:连接OA.∵DA平分∠BDE,∴∠BDA=∠EDA.∵OA=OD,∴∠ODA=∠OAD.∴∠OAD=∠EDA.∴OA∥CE.∵AE⊥DE,∴∠AED=90°,∴∠OAE=∠DEA=90°.∴AE⊥OA.∴AE是⊙O的切线.(2)∵BD是直径,∴∠BCD=∠BAD=90°.∵∠DBC=30°,∴∠BDC=60°.∴∠BDE=120°.∵DA平分∠BDE,∴∠BDA=∠EDA=60°.∴∠ABD=∠EAD=30°.在Rt△AED中,∠AED=90°,∠EAD=30°,∴AD=2DE.在Rt△ABD中,∠BAD=90°,∠ABD=30°,∴BD=2AD=4DE.∵DE的长是1 cm,∴BD的长是4 cm.。