下载文档原格式
第十二章超静定系统12-1 试问下列结构(梁或刚架)中那些是静定的?哪些是超静定的?若是超静定的,试说明它的次数。
答：a , 静定b , f , 一次超静定d ,e , 二次超静定g , h , 三次超静定c , 几何可变12-2 试求下列各超静定梁的支反力，设各梁均为等截面梁，其抗弯刚度为EI。
a)解：图a 可分解如下图0=+BR BP f f ---------（1） EIL R f EIPL L L EIPlf B BR BP 3485)23(2432=-=--=代入（1）式得 163;)(1611;)(165PL MR P R AA B =↑=↑=（ ）b)解：设支承B 反力为B R由P 和B R 共同作用下B 点的总挠度要求为零，即有 ()()↓=↑==+-⨯-=+P R P EI L R L L EIPLf f C B BR BP 43;47R 03)5.13(60B 32PL MC41=（⌫）c)解：设支承B 反力为B R ，则必定有0=+BR BP f f ---------（1）EIlR EIl R f EIb l Pb f B B BR BP 648)2(48]4)2(3[3322==--=代入(1)式 得 3222)3(lb l Pb R B -=d)解：0M MA-= （ ）)(23)(2323;23,3)(,2002032↓=↑+==-=--=-==+lM R P l M R lM P R EIl M l EIP R l EIP R f EI Mlf f f A B B B B BRP BM BRP BMe)解：e 图可由下图e ’和e ”叠加而成因为BB RB qp RB qp R EIlEIl R f qlEIl l EIl ql l EIqlEI qlf f f 383)2(4895)236(6))((68)1(033422334==-=--⋅--=-----=+代入（1）式得 )(12895↑=q l R B ； )(256`161↑=q l R A ；26433q l MA-= （ ）f)解：A , B 端转角为零，则有：0,0=+BAMAMAq θθ ----------（1） 0,0=+BAMBMBq θθ ----------（2）式中，EIlq Aq 3608300-=θ ； EIlq Bq 3607300=θEI lMEI lMBAMAMBA63,⋅+⋅=θEIlMEIlMABMBMBA63,⋅-⋅-=θ将以上θ表达式代入（1），（2）联立求解得：20201l q MA=； 20301l q MB=； l q R A 0207= ； l q R B 0203=12-3 梁AB 的一端固定，另端由拉杆拉住，梁与杆系用同一材料两成，其弹性模量为E ，梁截面惯矩为I ，拉杆的截面积为A ，梁上承受均布载荷q ，试求拉杆BC 的内力。
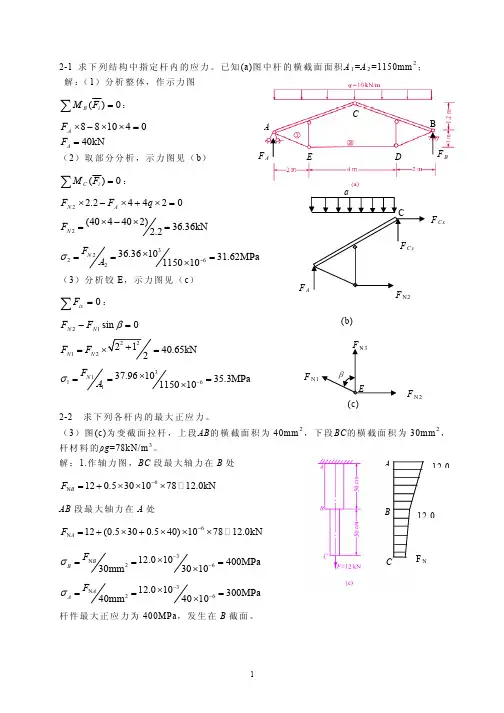
2-1 求下列结构中指定杆内的应力。
已知(a)图中杆的横截面面积A 1=A 2=1150mm 2； 解：（1）分析整体，作示力图∑=0)(i BF M：CB 041088=××−×A F AF N1F N2(c)40kN A F =（2）取部分分析，示力图见（b ）∑=0)(i CF M：02442.22=×+×−×q F F A N2(404402)36.36kN 2.2N F ×−×==3262236.361031.62MPa 115010N F A σ−×===×（3）分析铰E ，示力图见（c ）∑=0ix F ：0sin 12=−βN N F F1240.65kN N N F F == 3161137.961035.3MPa 115010N F A σ−×===×2-2 求下列各杆内的最大正应力。
（3）图(c)为变截面拉杆，上段AB 的横截面积为40mm 2，下段BC 的横截面积为30mm 2，杆材料的ρg =78kN/m 3。
解：1.作轴力图，BC 段最大轴力在B 处6N 120.530107812.0kN B F −=+×××AB 段最大轴力在A 处6N 12(0.5300.540)107812.0kN A F −=+×+×××3N 2612.010400MPa 30mm3010B B F σ−−×===× 3N 2612.010300MPa 40mm 4010AA F σ−−×===×杆件最大正应力为400MPa ，发生在B 截面。
EDF BF AF CxF N2(b)A120B120F NC2-4 一直径为15mm ，标距为200mm 的合金钢杆，比例极限内进行拉伸试验，当轴向荷载从零缓慢地增加58.4kN 时，杆伸长了0.9mm ，直径缩小了0.022mm ，确定材料的弹性模量E 、泊松比µ。
材料力学-学习指导及习题答案第一章绪论1-1 图示圆截面杆，两端承受一对方向相反、力偶矩矢量沿轴线且大小均为M的力偶作用。
试问在杆件的任一横截面m-m上存在何种内力分量，并确定其大小。
解：从横截面m-m将杆切开，横截面上存在沿轴线的内力偶矩分量M x，即扭矩，其大小等于M。
1-2 如图所示，在杆件的斜截面m-m上，任一点A处的应力p=120 MPa，其方位角θ=20°，试求该点处的正应力σ与切应力τ。
解：应力p与斜截面m-m的法线的夹角α=10°，故σ＝p cosα=120×cos10°=118.2MPaτ＝p sinα=120×sin10°=20.8MPa1-3 图示矩形截面杆，横截面上的正应力沿截面高度线性分布，截面顶边各点处的正应力均为σmax=100 MPa，底边各点处的正应力均为零。
试问杆件横截面上存在何种内力分量，并确定其大小。
图中之C点为截面形心。
解：将横截面上的正应力向截面形心C简化，得一合力和一合力偶，其力即为轴力F N=100×106×0.04×0.1/2=200×103 N =200 kN其力偶即为弯矩M z=200×(50-33.33)×10-3 =3.33 kN·m1-4 板件的变形如图中虚线所示。
试求棱边AB与AD的平均正应变及A点处直角BAD的切应变。
解：第二章轴向拉压应力2-1试计算图示各杆的轴力，并指出其最大值。
解：(a) F N AB=F, F N BC=0, F N，max=F(b) F N AB=F, F N BC=－F, F N，max=F(c) F N AB=－2 kN, F N2BC=1 kN, F N CD=3 kN, F N，max=3 kN(d) F N AB=1 kN, F N BC=－1 kN, F N，max=1 kN2-2 图示阶梯形截面杆AC，承受轴向载荷F1=200 kN与F2=100 kN，AB段的直径d1=40 mm。
轴向拉压1. 等截面直杆CD 位于两块夹板之间，如图示。
杆件与夹板间的摩擦力与杆件自重保持平衡。
设杆CD 两侧的摩擦力沿轴线方向均匀分布，且两侧摩擦力的集度均为q ，杆CD 的横截面面积为A ，质量密度为ρ，试问下列结论中哪一个是正确的？ (A)gA q ρ=；(B) 杆内最大轴力ql F =maxN ；(C) 杆内各横截面上的轴力2N gAlF ρ=；(D) 杆内各横截面上的轴力0N =F 。
2. 低碳钢试样拉伸时，横截面上的应力公式A F N =σ适用于以下哪一种情况?(A) 只适用于σ≤p σ； (B) 只适用于σ≤e σ； (C) 只适用于σ≤s σ； (D) 在试样拉断前都适用。
3. 在A 和B 两点连接绳索ACB ，绳索上悬挂物重P ，如图示。
点A 和点B 的距离保持不变，绳索的许用拉应力为][σ。
试问：当α角取何值时，绳索的用料最省？ (A) 0； (B) 30； (C) 45； (D) 60。
4. 桁架如图示，载荷F 可在横梁（刚性杆）DE 上自由移动。
杆1和杆2的横截面面积均为A ，许用应力均为][σ（拉和压相同）。
求载荷F 的许用值。
以下四种答案中哪一种是正确的？ (A) 2][A σ； (B) 3][2Aσ； (C) A ][σ；(D)A ][2σ。
5. 设受力在弹性范围内，问空心圆杆受轴向拉伸时，外径与壁厚的下列四种变形关系中哪一种是正确的？ (A) 外径和壁厚都增大； (B) 外径和壁厚都减小； (C) 外径减小，壁厚增大； (D) 外径增大，壁厚减小。
6. 三杆结构如图所示。
今欲使杆3的轴力减小，问应采取以下哪一种措施？(A) 加大杆3的横截面面积； CDqqlaABααC PCADaaaaBEF21αα132(B) 减小杆3的横截面面积； (C) 三杆的横截面面积一起加大； (D) 增大α角。
7. 图示超静定结构中，梁AB 为刚性梁。
设1l ∆和2l ∆分别表示杆1的伸长和杆2的缩短，试问两斜杆间的变形协调条件的正确答案是下列四种答案中的哪一种? (A) βαsin 2sin 21l l ∆=∆； (B) βαcos 2cos 21l l ∆=∆； (C) αβsin 2sin 21l l ∆=∆；(D) αβcos 2cos 21l l ∆=∆。
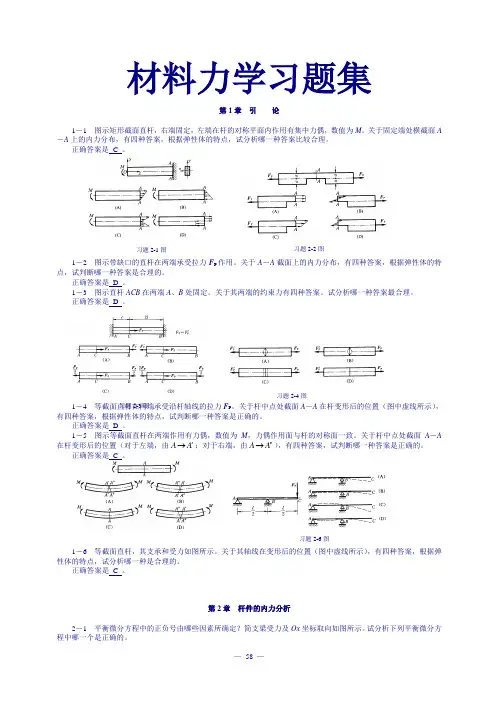
习题2-1图 习题2-2图 习题2-3图 习题2-4图 习题2-5图 习题2-6图 材料力学习题集第1章 引 论1－1 图示矩形截面直杆，右端固定，左端在杆的对称平面内作用有集中力偶，数值为M 。
关于固定端处横截面A －A 上的内力分布，有四种答案，根据弹性体的特点，试分析哪一种答案比较合理。
正确答案是 C 。
1－2 图示带缺口的直杆在两端承受拉力F P 作用。
关于A －A 截面上的内力分布，有四种答案，根据弹性体的特点，试判断哪一种答案是合理的。
正确答案是 D 。
1－3 图示直杆ACB 在两端A 、B 处固定。
关于其两端的约束力有四种答案。
试分析哪一种答案最合理。
正确答案是 D 。
1－4 等截面直杆在两端承受沿杆轴线的拉力F P 。
关于杆中点处截面A －A 在杆变形后的位置（图中虚线所示），有四种答案，根据弹性体的特点，试判断哪一种答案是正确的。
正确答案是 D 。
1－5 图示等截面直杆在两端作用有力偶，数值为M ，力偶作用面与杆的对称面一致。
关于杆中点处截面A －A 在杆变形后的位置（对于左端，由A A '→；对于右端，由A A ''→），有四种答案，试判断哪一种答案是正确的。
正确答案是 C 。
1－6 等截面直杆，其支承和受力如图所示。
关于其轴线在变形后的位置（图中虚线所示），有四种答案，根据弹性体的特点，试分析哪一种是合理的。
正确答案是 C 。
第2章 杆件的内力分析2－1 平衡微分方程中的正负号由哪些因素所确定？简支梁受力及Ox 坐标取向如图所示。
试分析下列平衡微分方程中哪一个是正确的。
习题2-1图习题2-2图习题2-3图习题2-4图（A d Q F d M（B （C （D 2－2 对于图示承受均布载荷q 的简支梁，其弯矩图凸凹性与哪些因素相关？试判断下列四种答案中哪几种是正确的。
2－3 已知梁的剪力图以及a 、e 截面上的弯矩M a 和M e ，如图所示。
第十三章 交 变 应 力
13.1火车轮轴受力情况如图所示。
a =500mm,l =1435mm,轮轴中段直径d =15cm 。
若P =50kN,试求轮轴中段截面边缘上任一点的最大应力
σmax 、最小应力σmin 、循环特征r ,并作出σ-t 曲线。
(原图见教P141.) 解：22615.05.01050max /5.75/105.753
323332m MN m N d Pa W M
=⨯====⨯⨯⨯ππσ
1
/5.755.755.752
max min max min
-===-=-=-σσσσr m MN 13.5货车轮轴两端载荷P=110kN ，材料为车轴钢,σb =500MPa,σ-1=240Mpa 。
规定安全系数n =1.5。
试校核Ⅰ—Ⅰ和Ⅱ—Ⅱ截面的强度。
（原图见教材P142.）
解：校核Ⅰ—Ⅰ截面的强度：
23.1/9.72/9.72/109.721081332max min 226108.0082.010110108.0082.0max 3323332==-=-==⨯====
⨯⨯⨯⨯⨯d D
P W M m MN m MN m N σσσππ
由教材图13-8（c ）查得：当2/500m MN b =σ时，34.1=σK
由教材表13-1查得： 当mm d 108=时，碳钢70.0=σε
由教材表13-2查得： 当2/400m MN b =σ时，车削加工，95.0=β
当2/800m MN b =σ时，车削加工，90.0=β
用插入法求得： 当2/500m MN b =σ时，车削加工，94.0=β
根据教材（13-11）式可知：5.162.19.7224094.070.034.1m ax 1====
⨯⨯-n n K σσσβσεσ
校核Ⅱ—Ⅱ截面的强度 ：
226133.0118.010110133.0118.0max /2.56/102.563333
3m MN m N P W M =⨯====⨯⨯⨯⨯⨯ππσ 2max min /2.56m MN -=-=σσ
3.013340==d r
； 1
.1133146
==d D
由教材图13-8（a ）查得：当2/500m MN b =σ时，2
.1=σK
由教材表13-1查得：当mm d 133=时，碳钢68.0=ε
由教材表13-2查得：当2/400m NM b =σ时，粗车加工，85.0=β
当2/800m MN σ时，粗车加工，80.0=β
用插入法求得：当2/800m MN b =σ时，粗车加工，84.0=β
根据教材（13-11）式可知：5.103.22.5624084.068.02.1m ax 1
=>===⨯⨯-n n K σσσβσεσ
结论：车轴强度足够。
13.6在σm -σa 坐标系中，标出与图示应力循环对应的原点，并求出自原点出发并通过这些点的射线与σm 轴的夹角a 。
解：（b ）'2663;2011113
1120403131max min ====
-===
-++--a tga r r r σσ (d) 5120040max min
===
σσr
'4133;6667.00111151
15====+-+-a tga r r
200。
