用R软件实现一元线性回归

一元回归r系数推导
一元回归分析中的R系数，也称为相关系数或者简单相关系数，用于衡量自变量和因变量之间的线性相关程度。

R系数的平方则表
示回归方程对因变量变异的解释程度。

要推导一元回归的R系数，我们首先需要计算相关系数。

相关
系数r的计算公式为：
r = Σ((X X̄)(Y Ȳ)) / √(Σ(X X̄)²Σ(Y Ȳ)²)。

其中，Σ表示求和，X̄和Ȳ分别表示自变量X和因变量Y的
平均值。

接下来，我们计算R系数的平方，即R²。

R²表示因变量的变
异中能够被自变量解释的比例，计算公式为：
R² = r²。

这样，我们就得到了一元回归的R系数。

R²的取值范围在0到
1之间，越接近1表示回归方程对因变量的解释能力越强，即自变
量和因变量之间的线性关系越密切。

除了R系数，我们还可以通过F检验、调整R²等指标来评估回归模型的拟合程度和解释能力。

需要注意的是，R系数只能反映自变量和因变量之间的线性相关程度，对于非线性关系的刻画能力有限。

在实际应用中，我们还需要结合实际情况和领域知识，综合考量多个指标来全面评估回归模型的质量和可靠性。

27. 回归分析回归分析是研究一个或多个变量（因变量）与另一些变量（自变量）之间关系的统计方法。

主要思想是用最小二乘法原理拟合因变量与自变量间的最佳回归模型（得到确定的表达式关系）。

其作用是对因变量做解释、控制、或预测。

回归与拟合的区别：拟合侧重于调整曲线的参数，使得与数据相符；而回归重在研究两个变量或多个变量之间的关系。

它可以用拟合的手法来研究两个变量的关系，以及出现的误差。

回归分析的步骤：（1）获取自变量和因变量的观测值；（2）绘制散点图，并对异常数据做修正；（3）写出带未知参数的回归方程；（4）确定回归方程中参数值；（5）假设检验，判断回归方程的拟合优度；（6）进行解释、控制、或预测。

（一）一元线性回归一、原理概述1. 一元线性回归模型：Y=0+1X+ε其中X是自变量，Y是因变量，0,1是待求的未知参数，0也称为截距；ε是随机误差项，也称为残差，通常要求ε满足：① ε的均值为0；② ε的方差为 2；③ 协方差COV(εi , εj )=0，当i≠j 时。

即对所有的i≠j, εi 与εj 互不相关。

用最小二乘法原理，得到最佳拟合效果的01ˆˆ,ββ值： 1121()()ˆ()n i i i nii x x y y x x β==--=-∑∑， 01ˆˆy x ββ=- 2.模型检验(1) 拟合优度检验计算R 2，反映了自变量所能解释的方差占总方差的百分比，值越大说明模型拟合效果越好。

通常可以认为当R 2大于0.9时，所得到的回归直线拟合得较好，而当R 2小于0.5时，所得到的回归直线很难说明变量之间的依赖关系。

(2) 回归方程参数的检验回归方程反应了因变量Y 随自变量X 变化而变化的规律，若 1=0，则Y 不随X 变化，此时回归方程无意义。

所以，要做如下假设检验：H 0: 1=0, H 1: 1≠0；① F 检验若 1=0为真，则回归平方和RSS 与残差平方和ESS/(N-2)都是 2的无偏估计，因而采用F 统计量：来检验原假设β1=0是否为真。

【机器学习笔记】⼀元线性回归原理、公式及代码实现概要线性回归是逻辑回归的基础，逻辑回归⼜是神经⽹络的组成部分，⽤于解决2分类问题线性回归是所有算法的基础线性关系与⾮线性关系概念：线性关系是指变量之间的关系是⼀次函数，⼀个⾃变量x和因变量y的关系表⽰为⼀条直线，两个⾃变量和因变量y的关系表⽰为⼀个平⾯⾮线性关系是指⼀个⾃变量x和因变量y的关系表⽰为⼀条曲线，两个⾃变量和因变量y的关系表⽰为⼀个曲⾯⼀个⾃变量x就等同于⼀个特征，拟合的时候就是⼀条线，⽽如果是多个特征，则是拟合⾯线性关系可以理解为就是⼀次函数，不管有多少个⾃变量⽰例：线性关系：y=a×x+b⾮线性关系：y=x2回归问题概念：预测⼀个连续问题的数值，线性回归主要⽤于处理回归问题，少数情况⽤于处理分类问题⼀元线性回归概念：⽤来描述⾃变量和因变量都只有⼀个（⼀个⾃变量称为⼀元）的情况，且⾃变量和因变量之间呈线性关系（⼀次函数）的回归模型表⽰形式：y=a×x+b只有x⼀个⾃变量，y为因变量，a为斜率，也称为x的权重，b为截距作⽤：通过⼀元线性回归模型寻找到⼀条合适的直线，最⼤程度地拟合⾃变量 x 和因变量 y 之间的关系，这样我们知道⼀个 x 的值，就可以通过这条拟合的直线找到最可能的 y学习⼀元线性模型的过程就算通过训练数据得到合适的a和b的过程，也就是该⼀元线性模型的参数即为 a 和 b，当输⼊⼀个新的测试数据点的时候，我们可以通过训练好的模型来进⾏预测。

模型好坏评价⽅式⽬标：预测值与真实值之间的差距越⼩越好，距离越⼩，代表我们的模型效果越好很⾃然的⼀个想法是：对于每⼀个点（x）都计算y−y_predict然后将所有的值进⾏累加最后除以样本数，这样是为了减少样本对于结果的影响。

公式：1 nn∑i=1(y i−y_predict i)这个公式存在的问题：预测出来的值有可能⼤于真实值也可能⼩于真实值，这将导致误差被虚弱，正负中和导致最终累加误差接近于 0改进：对每个点的误差计算取绝对值，也就是|y i−y_predict i|，之后我们再进⾏累加问题：后续的误差计算以及求导问题绝对值函数，⽐如y=|x|在x=0处连续，但是在x处左导数为-1，右导数为1，不相等，可导函数必须光滑，所以函数在x=0不可导进⼀步优化：对于每个点计算得到的误差，对这个结果做⼀次平⽅，并且为了忽略样本数的影响，取平均值公式：Processing math: 100%1 nn∑i=1(y i−y_predict i)2最⼩⼆乘法由于y_predict i=ax i+b 代⼊上⼀节的公式中1 nn∑i=1(y i−ax i−b)2通过最⼩⼆乘法来寻找最优的参数 a 和 b，从⽽使这个表达式尽可能的⼩概念：⼀种数学优化技术，通过最⼩化误差的平⽅和来寻找最优的参数公式：a=∑n i=1(x i−¯x)(y i−¯y)∑n i=1(x i−¯x)2 b=¯y−a¯x代码实现import numpy as npfrom matplotlib import pyplot as pltif __name__ == '__main__':# 准备数据x = np.array([1, 2, 4, 6, 8]) # ⼀元线性回归模型仅处理向量，⽽不能处理矩阵 y = np.array([2, 5, 7, 8, 9])x_mean = np.mean(x)y_mean = np.mean(y)# 求a和bdenominator = 0.0 # 分母numerator = 0.0 # 分⼦for x_i, y_i in zip(x, y): # 将x, y向量合并起来形成元组(1, 2)、(2, 5)numerator += (x_i - x_mean) * (y_i - y_mean)denominator += (x_i - x_mean) ** 2a = numerator / denominatorb = y_mean - a * x_mean# ⽤a和b构造线性函数，输出的预测值存⼊y_predicty_predict = a * x + b # 这个函数是⾮常拟合训练集x的# 画出这条直线，以及训练集的数据plt.scatter(x, y, color='b')plt.plot(x, y_predict, color='r')plt.xlabel('x', fontsize=15)plt.ylabel('y', fontsize=15)plt.show()# 输⼊测试数据，回归⼀个值x_test = 7y_predict_test = a * x_test + bprint(y_predict_test)⼀元线性回归模型仅处理向量，⽽不能处理矩阵进⾏⼀定的封装以后：import numpy as npimport matplotlib.pyplot as pltclass SimpleLinearRegressionSelf:# 初始化变量def __init__(self):"""初始化simple linear regression模型"""self.a_ = None # 类内使⽤，⾮⽤户外部输⼊的变量self.b_ = None # 类内使⽤，⾮⽤户外部输⼊的变量# 训练模型def fit(self, x_train, y_train):assert x_train.ndim == 1x_mean = np.mean(x_train)y_mean = np.mean(y_train)denominator = 0.0numerator = 0.0for x_i, y_i in zip(x_train, y_train):numerator += (x_i - x_mean) * (y_i - y_mean)denominator += (x_i - x_mean) ** 2self.a_ = numerator / denominatorself.b_ = y_mean - self.a_ * x_meanreturn self# 预测def predict(self, x_test_group): # 输⼊的是向量集合# 对输⼊向量集合中的每⼀个向量都进⾏⼀次预测，预测的具体实现被封装在_predict函数中 return np.array([self._predict(x_test) for x_test in x_test_group])def _predict(self, x_test):# 求每⼀个输⼊的x_test以得到预测值return self.a_ * x_test + self.b_# 衡量模型分数def mean_squared_error(self, y_true, y_predict):return np.sum((y_true - y_predict) ** 2) / len(y_true)def r_square(self, y_true, y_predict):# 计算指定数据（数组元素）沿指定轴的⽅差return 1 - (self.mean_squared_error(y_true, y_predict) / np.var(y_true))if __name__ == '__main__':x = np.array([1, 2, 4, 6, 8])y = np.array([2, 5, 7, 8, 9])lr = SimpleLinearRegressionSelf()lr.fit(x, y)print(lr.predict([7]))print(lr.r_square([8, 9], lr.predict([6, 8])))此处衡量模型分数的公式为：R2=1−1n∑ni=1(y_predict i−y i)2∑n i=1(¯y−y i)2。

r语言建立标准化回归方程一、简介标准化回归方程是一种在统计学中常用的方法，主要用于量化两个或多个变量之间的线性关系。

通过标准化，我们可以消除变量间的单位差异，使得回归分析更加准确。

在R语言中，我们可以使用内置的统计函数轻松地建立标准化回归方程。

二、步骤1.数据准备：首先，我们需要准备包含自变量和因变量的数据集。

确保数据已经进行了适当的清理和预处理。

2.加载R语言统计包：在R语言中，我们需要使用相应的统计包来进行回归分析。

常用的统计包包括“stats”和“ggplot2”。

3.标准化数据：使用R语言的“scale”函数对数据进行标准化处理，将所有变量都转换为无量纲值。

4.建立回归方程：使用“lm”函数或“glm”函数（适用于多元线性回归模型）来建立标准化回归方程。

5.模型评估：使用R语言的内置统计函数（如“summary”函数）对模型进行评估，包括模型系数、R方值、调整R方值等。

三、示例代码以下是一个使用R语言建立标准化回归方程的示例代码：```r#加载所需的统计包library(stats)library(ggplot2)#准备数据集，假设我们有一个包含自变量x和因变量y的数据集datadata<-data.frame(x=c(1,2,3,4,5),y=c(2.5,3.7,4.9,5.8,6.5)) #对数据进行标准化处理data_scaled<-scale(data)#建立标准化回归方程，这里我们使用多元线性回归模型model<-lm(y~x,data=data_scaled)#输出模型摘要，评估模型性能summary(model)```四、结果解释标准化回归方程的输出将包括模型的系数、标准误差、t值和p 值等统计信息。

这些信息可以帮助我们理解自变量和因变量之间的关系强度和方向。

通常，系数较大的值表示该自变量对因变量的影响较大，而t值和p值则可以用于判断该关系是否具有统计学意义。

一元线性回归r方
一元线性回归r方是一种常见的统计分析方法，用于描述
两个变量之间的关系，以及预测未知数据的趋势。

它最常用于分析解释变量与因变量之间的关系，也可以用于检验现有的理论假设。

一元线性回归r方的计算方法是，首先，通过线性回归拟
合出一条最优回归线，然后计算出该回归线和实际数据之间的相关性，从而得出一元线性回归r方的值。

一元线性回归r方
的值介于0到1之间，其中1表示完美拟合，0表示没有拟合。

一元线性回归r方的应用非常广泛，可以用于统计分析，
市场调研，经济预测，社会科学，金融投资等多个领域。

它可以帮助我们分析解释变量（如价格，汇率，收入）与因变量（如消费，投资，利润）之间的关系，从而为决策者提供有效的决策参考。

此外，一元线性回归r方还可以用于预测未知数
据的变化趋势，帮助企业管理者有效地分析市场，进而采取有效的策略。

总之，一元线性回归r方是一个非常实用的统计分析方法，可以用于分析变量之间的关系，以及预测未知数据的趋势，为企业管理者提供有效的决策参考，提高企业的经营管理水平。

多元线性回归公式推导及R语⾔实现多元线性回归多元线性回归模型实际中有很多问题是⼀个因变量与多个⾃变量成线性相关，我们可以⽤⼀个多元线性回归⽅程来表⽰。

为了⽅便计算，我们将上式写成矩阵形式:Y = XW假设⾃变量维度为NW为⾃变量的系数，下标0 - NX为⾃变量向量或矩阵，X维度为N,为了能和W0对应，X需要在第⼀⾏插⼊⼀个全是1的列。

Y为因变量那么问题就转变成，已知样本X矩阵以及对应的因变量Y的值，求出满⾜⽅程的W，⼀般不存在⼀个W是整个样本都能满⾜⽅程，毕竟现实中的样本有很多噪声。

最⼀般的求解W的⽅式是最⼩⼆乘法。

最⼩⼆乘法我们希望求出的W是最接近线性⽅程的解的，最接近我们定义为残差平⽅和最⼩，残差的公式和残差平⽅和的公式如下：上⾯的公式⽤最⼩残差平⽅和的⽅式导出的，还有⼀种思路⽤最⼤似然的⽅式也能推导出和这个⼀样的公式，⾸先对模型进⾏⼀些假设：误差等⽅差不相⼲假设，即每个样本的误差期望为0，每个样本的误差⽅差都为相同值假设为σ误差密度函数为正态分布 e ~ N(0, σ^2)简单推导如下:由此利⽤最⼤似然原理导出了和最⼩⼆乘⼀样的公式。

最⼩⼆乘法求解⼆次函数是个凸函数，极值点就是最⼩点。

只需要求导数=0解出W即可。

模拟数据我们这⾥⽤R语⾔模拟实践⼀下，由于我们使⽤的矩阵运算，这个公式⼀元和多元都是兼容的，我们为了可视化⽅便⼀点，我们就⽤R语⾔⾃带的women数据做⼀元线性回归，和多元线性回归的⽅式基本⼀样。

women数据如下> womenheight weight1 58 1152 59 1173 60 1204 61 1235 62 1266 63 1297 64 1328 65 1359 66 13910 67 14211 68 14612 69 15013 70 15414 71 15915 72 164体重和⾝⾼具有线性关系，我们做⼀个散点图可以看出来：我们⽤最⼩⼆乘推导出来的公式计算w如下X <- cbind(rep(1, nrow(women)), women$height)X.T <- t(X)Y <- women$weightw <- solve(X.T %*% X) %*% X.T %*% Y> w[,1][1,] -87.51667[2,] 3.45000> lm.result <- lm(women$weight~women$height)> lm.resultCall:lm(formula = women$weight ~ women$height)Coefficients:(Intercept) women$height-87.52 3.45上⾯的R代码w使我们利⽤公式计算出来的，下边是R语⾔集成的线性回归函数拟合出来的，可以看出我们的计算结果是正确的，lm的只是⼩数点取了两位⽽已，将回归出来的函数画到图中看下回归的效果。

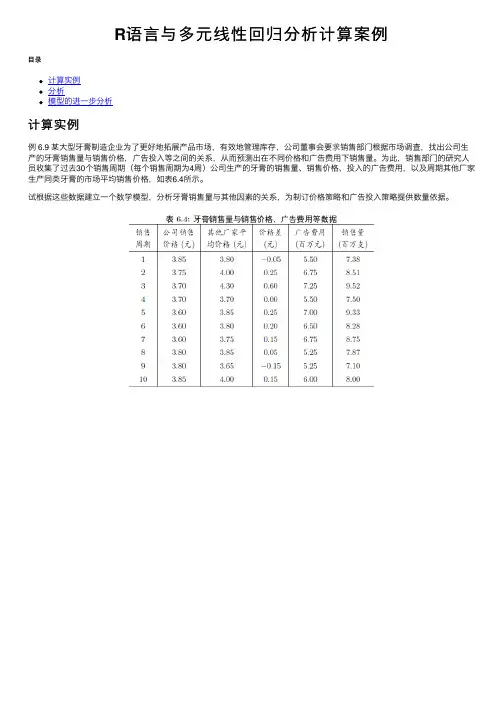
R语⾔与多元线性回归分析计算案例⽬录计算实例分析模型的进⼀步分析计算实例例 6.9 某⼤型⽛膏制造企业为了更好地拓展产品市场，有效地管理库存，公司董事会要求销售部门根据市场调查，找出公司⽣产的⽛膏销售量与销售价格，⼴告投⼊等之间的关系，从⽽预测出在不同价格和⼴告费⽤下销售量。

为此，销售部门的研究⼈员收集了过去30个销售周期（每个销售周期为4周）公司⽣产的⽛膏的销售量、销售价格、投⼊的⼴告费⽤，以及周期其他⼚家⽣产同类⽛膏的市场平均销售价格，如表6.4所⽰。

试根据这些数据建⽴⼀个数学模型，分析⽛膏销售量与其他因素的关系，为制订价格策略和⼴告投⼊策略提供数量依据。

分析由于⽛膏是⽣活的必需品，对于⼤多数顾客来说，在购买同类⽛膏时，更多的会关⼼不同品牌之间的价格差，⽽不是它们的价格本⾝。

因此，在研究各个因素对销售量的影响时，⽤价格差代替公司销售价格和其他⼚家平均价格更为合适。

模型的建⽴与求解记⽛膏销售量为Y，价格差为X1，公司的⼴告费为X2，假设基本模型为线性模型:输⼊数据，调⽤R软件中的lm（）函数求解，并⽤summary（）显⽰计算结果（程序名：exam0609.R）计算结果通过线性回归系数检验和回归⽅程检验，由此得到销售量与价格差与⼴告费之间的关系为：模型的进⼀步分析为进⼀步分析回归模型，我们画出y与x1和y与x2散点图。

从散点图上可以看出，对于y与x1，⽤直线拟合较好。

⽽对于y与x2，则⽤⼆次曲线拟合较好，如下图：绘制x1与y的散点图和回归直线绘制x2与y的散点图和回归曲线其中 I(X2^2)，表⽰模型中X2的平⽅项，及X22，从上图中，将销售量模型改为：似乎更合理，我们做相应的回归分析：此时，我们发现，模型残差的标准差Residual standard error有所下降，相关系数的平⽅Multiple R-squared有所上升，这说明模型修正的是合理的。

但同时也出现了⼀个问题，就是对于β2的P-值>0.05。

一元线性回归分析实验报告.doc一、实验目的本实验旨在通过一元线性回归模型，探讨两个变量之间的关系，即一个变量是否随着另一个变量的变化而呈现线性变化。

通过实际数据进行分析，理解一元线性回归模型的应用及其局限性。

二、实验原理一元线性回归是一种基本的回归分析方法，用于研究两个连续变量之间的关系。

其基本假设是：因变量与自变量之间存在一种线性关系，即因变量的变化可以由自变量的变化来解释。

一元线性回归的数学模型可以表示为：Y = aX + b，其中Y是因变量，X是自变量，a是回归系数，b是截距。

三、实验步骤1.数据收集：收集包含两个变量的数据集，用于建立一元线性回归模型。

2.数据预处理：对数据进行清洗、整理和标准化，确保数据的质量和准确性。

3.绘制散点图：通过散点图观察因变量和自变量之间的关系，初步判断是否为线性关系。

4.建立模型：使用最小二乘法估计回归系数和截距，建立一元线性回归模型。

5.模型评估：通过统计指标（如R²、p值等）对模型进行评估，判断模型的拟合程度和显著性。

6.模型应用：根据实际问题和数据特征，对模型进行解释和应用。

四、实验结果与分析1.数据收集与预处理：我们收集了一个关于工资与工作经验的数据集，其中工资为因变量Y，工作经验为自变量X。

经过数据清洗和标准化处理，得到了50个样本点。

2.散点图绘制：绘制了工资与工作经验的散点图，发现样本点大致呈线性分布，说明工资随着工作经验的变化呈现出一种线性趋势。

3.模型建立：使用最小二乘法估计回归系数和截距，得到一元线性回归模型：Y = 50X + 2000。

其中，a=50表示工作经验每增加1年，工资平均增加50元；b=2000表示当工作经验为0时，工资为2000元。

4.模型评估：通过计算R²值和p值，对模型进行评估。

在本例中，R²值为0.85，说明模型对数据的拟合程度较高；p值为0.01，说明自变量对因变量的影响是显著的。

r语言多元线性回归模型
多元线性回归模型是最常用的统计分析方法之一，常用于模拟一些统计数据，衡量变量之间存在的某种影响关系。

多元线性回归模型可以用来确定影响因素，以及出现的预测值的变化趋势。

本文将介绍多元线性回归模型，以及如何使用R语言进行多元线性回归分析。

多元线性回归模型也称为多元回归，是一种用于描述两个或更多不同类型的变量之间关系的数据分析工具。

它通常用来分析多个解释变量（也称为自变量）与一个响应变量（也称为因变量）之间的相互作用和依赖关系。

主要思想是假定因变量和自变量之间存在线性关系，以及自变量的变化将导致因变量的变化，反之亦然。

R语言是一种对多元线性回归分析提供了良好支持的数
据分析工具。

要进行多元线性回归分析，首先需要选择合适的数据集。

接下来，使用R语言中的lm函数建立
模型，该函数可以接收参数x和y来确定因变量和自变量。

然后，使用summary函数对结果进行整理和汇总，获得每个变量的系数和参数估计值，并计算残差值。

最后，使用plot函数可以得到建立的模型的图像。

多元线性回归模型可以被用来研究一定定量变量之间的关系。

通过调整参数优化各个变量的回归，可以更准确地预测变量之间存在的关系，用以分析数据所暗示的影响关系，同时给出科学的建议和结果，用以指导实际的解决方案。

R语言是实现多元线性回归的有效数据分析工具，可以很好地帮助我们理解多变量之间的关系以及分析数据所蕴含的影响关系。

原创R语言线性回归案例数据分析可视化报告附代码数据在数据分析领域，线性回归是一种常用的数据建模和预测方法。

本文将使用R语言进行一个原创的线性回归案例分析，并通过数据可视化的方式呈现分析结果。

下面是我们的文本分析报告，同时包含相关的代码数据（由于篇幅限制，只呈现部分相关代码和数据）。

请您详细阅读以下内容。

1. 数据概述本次案例我们选用了一个关于房屋价格的数据集，数据包含了房屋面积、房间数量、地理位置等多个维度的信息。

我们的目标是分析这些因素与房屋价格之间的关系，并进行可视化展示。

2. 数据预处理在开始回归分析之前，我们需要对数据进行预处理，包括数据清洗和特征选择。

在这个案例中，我们通过删除空值和异常值来清洗数据，并选择了面积和房间数量两个特征作为自变量进行回归分析。

以下是示例代码：```R# 导入数据data <- read.csv("house_data.csv")# 清洗数据data <- na.omit(data)# 删除异常数据data <- data[data$area < 5000 & data$rooms < 10, ]# 特征选择features <- c("area", "rooms")target <- "price"```3. 线性回归模型建立我们使用R语言中的lm()函数建立线性回归模型，并通过summary()函数输出模型摘要信息。

以下是相关代码：```R# 线性回归模型建立model <- lm(data[, target] ~ ., data = data[, features])# 输出模型摘要信息summary(model)```回归模型摘要信息包含了拟合优度、自变量系数、截距等重要信息，用于评估模型的拟合效果和各个因素对因变量的影响程度。

⼀元线性回归的matlab实现（含R⽅和F分布检验）学习资料⼀元线性回归的m a t l a b实现(含R⽅和F分布检验)⼀元线性回归的matlab实现（含检验）【更新】说明：正⽂中命令部分可以直接在Matlab中运⾏，作者(Yangfd09_LZU)在MATLAB R2009a(7.8.0.347)中运⾏通过%求⼀元线性回归⽅程%数据要求：两⾏。

第⼀⾏存放x的观察值，第⼆⾏存放y的观察值%数据⽂件名：data_yyhg.mat；变量名：test%load data_yyhg.matN=length(test(1,:)); %注：也可以⽤[M,N]=size(test)% 但不能⽤N=size(test(1,:))sx=0;sx2=0;sy=0;sy2=0;sxy=0;Lxy=0;Lyy=0;for i=1:Nsx=sx+test(1,i);sx2=sx2+test(1,i)^2;sy=sy+test(2,i);sy2=sy2+test(2,i)^2;sxy=sxy+test(1,i)*test(2,i);Lxy=Lxy+(test(1,i)-sum(test(1,:))/N)*(test(2,i)-sum(test(2,:)/N)); Lyy=Lyy+(test(2,i)-sum(test(2,:))/N)^2;endr=[N,sx;sx,sx2]\[sy;sxy];a=r(1);b=r(2);%F分布检验U=b*Lxy;Q=Lyy-U;F=(N-2)*U/Q;%拟合优度检验x=test(1,:);y=a+b*x;eq=sum(test(2,:))/N;ssd=0;ssr=0;for i=1:Nssd=ssd+(test(2,i)-y(i))^2;ssr=ssr+(y(i)-eq)^2;endsst=ssd+ssr;RR=ssr/sst;%命令窗⼝中显⽰回归⽅程。