《计量经济学》eviews实验报告一元线性回归模型详解

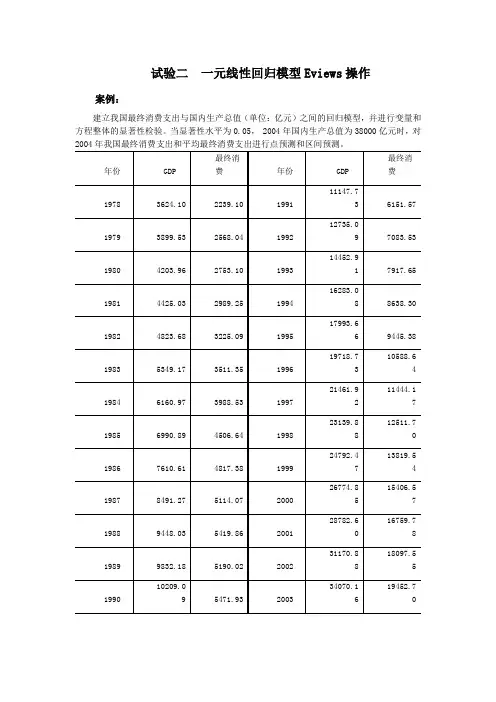
试验二一元线性回归模型Eviews操作案例：建立我国最终消费支出与国内生产总值（单位：亿元）之间的回归模型，并进行变量和方程整体的显著性检验。

当显著性水平为0.05， 2004年国内生产总值为38000亿元时，对2004年我国最终消费支出和平均最终消费支出进行点预测和区间预测。

一、创建工作文件建立工作文件的方法有以下几种。

1．菜单方式在主菜单上依次单击File→New→Workfile（见图2-1），选择数据类型和起止日期。

时间序列提供起止日期（年、季度、月度、周、日），非时间序列提供最大观察个数。

本例中在Start Data里输入1978，在End data 里输入2003，见图2-3。

单击OK后屏幕出现Workfile工作框，如图2-4所示。

2．命令方式在命令窗口直接输入建立工作文件的命令CREATE，命令格式：CREATE 数据频率起始期终止期其中，数据频率类型分别为A（年）、Q（季）、M（月）、U（非时间序列数据）。

输入Eviews 命令时，命令字与命令参数之间只能用空格分隔。

如本例可输入命令：CREATE A 1978 2003工作文件创立后，需将工作文件保存到磁盘，单击工具条中Save→输入文件名、路径→保存，或单击菜单兰中File→Save或Save as→输入文件名、路径→保存。

图2-1这时屏幕上出现Workfile Range对话框，如图2-2所示。

图2-2图2-3图2-4二、输入和编辑数据建立或调入工作文件以后，可以输入和编辑数据。

输入数据有两种基本方法：命令方式和菜单方式。

1．命令方式命令格式：data 〈序列名1〉〈序列名2〉…〈序列名n〉功能：输入新变量的数据，或编辑工作文件中现有变量的数据。

在本例中，在命令窗口直接输入：Data Y X2．菜单方式在主菜单上单击Objects→New object，在New object对话框里，选Group并在Name for Object上定义变量名（如变量X、Y），单击OK，屏幕出现数据编辑框。

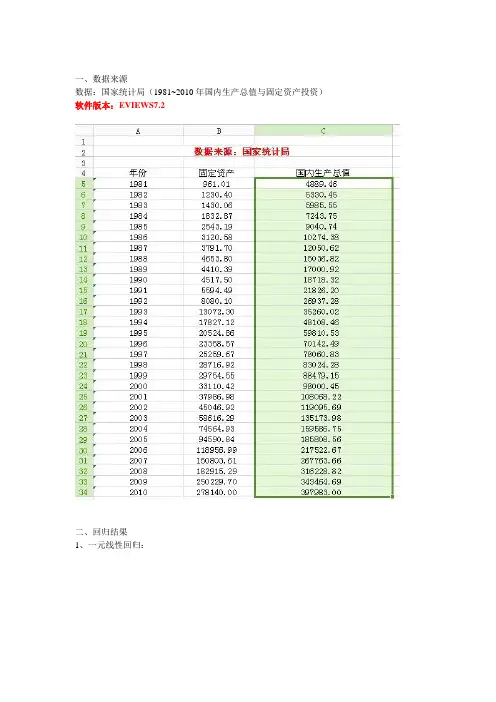
一、数据来源
数据：国家统计局（1981~2010年国内生产总值与固定资产投资）软件版本：EVIEWS7.2
二、回归结果
1、一元线性回归：
三、模型诊断与修正
DW检验：相关系数δ=0.8546，查表得，
1.35
1.49
L
U
d
d
=
=
经检验，DW<1.35,自变量呈一阶正自
相关
四、广义差分法修正后的结果
对E 进行滞后一期的自回归，可得回归方程：E=0.9337E(-1)
对原模型进行广义差分，输出结果为：
**ˆˆ6981.723 1.002749t t y x =+
由于使用广义差分数据，样本容量减少了1个，为29个。

查5%的显著性水平的DW
统计表可知， 1.341.48
L U d d ==，模型中的4-DU>DW>DU ，所以广义差分模型已无序列相关。

根据()1ˆˆ16981.723βρ-=，可得1
ˆ=105305.023β。

因此，原回归模型应为 105305.023 1.002749t t y x =+
采用普莱斯-文斯滕变换后第一个观测值变为211y δ-为1750.7019和211x δ-为344.1377，变换后普通最小二乘结果为**ˆˆ7555.503 1.0611t t y
x =+，根据()1ˆˆ17555.503βρ-=，得1
ˆ=113959.321β，由此，最终模型是 ˆ113959.321 1.0611t t y
x =+。

S .. . ..学生实验报告（经管类专业用）一、实验目的及要求：1、目的利用ＥＶＩＥＷＳ实验软件，使学生在实验过程中全面了解和熟悉计量经济学的基本概念，熟悉一元线性回归模型估计的基本程序和基本方法。

2、内容及要求(１)．熟悉ＥＶＩＥＷＳ实验软件的基本操作程序和方法；(2)、掌握一元线性回归模型基本概念，了解其估计和检验原理(3)、提交实验报告二、仪器用具：三、实验结果与数据处理：1 经研究发现，家庭书刊消费受家庭收入几户主受教育年数的影响，表中为对某地区部分. . . 资料. .8家庭抽样调查得到样本数据：(1) 建立家庭书刊消费的计量经济模型； （2）利用样本数据估计模型的参数；（3）检验户主受教育年数对家庭书刊消费是否有显著影响； （4）分析所估计模型的经济意义和作用 答：（1）建立家庭书刊消费的计量经济模型： i i i i u T X Y +++=321βββ其中：Y 为家庭书刊年消费支出、X 为家庭月平均收入、T 为户主受教育年数 （2即 ii i T X Y 3703.5208645.00162.50ˆ++-= （49.46026）（0.02936） （5.20217）t= (-1.) (2.) (10.06702)R 2=0. 944732.02=R F=146.2974(3) 检验户主受教育年数对家庭书刊消费是否有显著影响:由估计检验结果, 户主受教育年数参数对应的t 统计量为10.06702, 明显大于t 的临界值131.2)318(025.0=-t ，同时户主受教育年数参数所对应的P 值为0.0000，明显小于05.0=α，均可判断户主受教育年数对家庭书刊消费支出确实有显著影响。

（4）本模型说明家庭月平均收入和户主受教育年数对家庭书刊消费支出有显著影响，家庭月平均收入增加1元，家庭书刊年消费支出将增加0.086元，户主受教育年数增加1年，家庭书刊年消费支出将增加52.37元。

一元线性回归分析研究实验报告一元线性回归分析研究实验报告一、引言一元线性回归分析是一种基本的统计学方法，用于研究一个因变量和一个自变量之间的线性关系。

本实验旨在通过一元线性回归模型，探讨两个变量之间的关系，并对所得数据进行统计分析和解读。

二、实验目的本实验的主要目的是：1.学习和掌握一元线性回归分析的基本原理和方法；2.分析两个变量之间的线性关系；3.对所得数据进行统计推断，为后续研究提供参考。

三、实验原理一元线性回归分析是一种基于最小二乘法的统计方法，通过拟合一条直线来描述两个变量之间的线性关系。

该直线通过使实际数据点和拟合直线之间的残差平方和最小化来获得。

在数学模型中，假设因变量y和自变量x之间的关系可以用一条直线表示，即y = β0 + β1x + ε。

其中，β0和β1是模型的参数，ε是误差项。

四、实验步骤1.数据收集：收集包含两个变量的数据集，确保数据的准确性和可靠性；2.数据预处理：对数据进行清洗、整理和标准化；3.绘制散点图：通过散点图观察两个变量之间的趋势和关系；4.模型建立：使用最小二乘法拟合一元线性回归模型，计算模型的参数；5.模型评估：通过统计指标（如R2、p值等）对模型进行评估；6.误差分析：分析误差项ε，了解模型的可靠性和预测能力；7.结果解释：根据统计指标和误差分析结果，对所得数据进行解释和解读。

五、实验结果假设我们收集到的数据集如下：经过数据预处理和散点图绘制，我们发现因变量y和自变量x之间存在明显的线性关系。

以下是使用最小二乘法拟合的回归模型：y = 1.2 + 0.8x模型的R2值为0.91，说明该模型能够解释因变量y的91%的变异。

此外，p 值小于0.05，说明我们可以在95%的置信水平下认为该模型是显著的。

误差项ε的方差为0.4，说明模型的预测误差为0.4。

这表明模型具有一定的可靠性和预测能力。

六、实验总结通过本实验，我们掌握了一元线性回归分析的基本原理和方法，并对两个变量之间的关系进行了探讨。

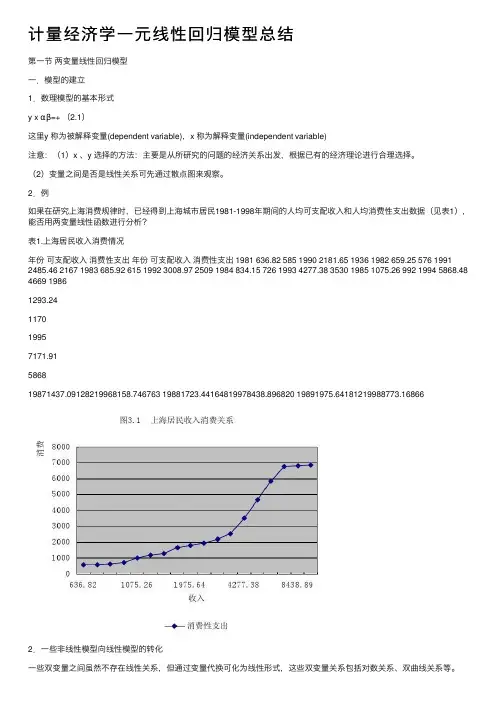
计量经济学⼀元线性回归模型总结第⼀节两变量线性回归模型⼀．模型的建⽴1．数理模型的基本形式y x αβ=+ （2.1）这⾥y 称为被解释变量(dependent variable)，x 称为解释变量(independent variable)注意：（1）x 、y 选择的⽅法：主要是从所研究的问题的经济关系出发，根据已有的经济理论进⾏合理选择。

（2）变量之间是否是线性关系可先通过散点图来观察。

2．例如果在研究上海消费规律时，已经得到上海城市居民1981-1998年期间的⼈均可⽀配收⼊和⼈均消费性⽀出数据（见表1），能否⽤两变量线性函数进⾏分析？表1.上海居民收⼊消费情况年份可⽀配收⼊消费性⽀出年份可⽀配收⼊消费性⽀出 1981 636.82 585 1990 2181.65 1936 1982 659.25 576 1991 2485.46 2167 1983 685.92 615 1992 3008.97 2509 1984 834.15 726 1993 4277.38 3530 1985 1075.26 992 1994 5868.48 4669 19861293.24117019957171.91586819871437.09128219968158.746763 19881723.44164819978438.896820 19891975.64181219988773.168662．⼀些⾮线性模型向线性模型的转化⼀些双变量之间虽然不存在线性关系，但通过变量代换可化为线性形式，这些双变量关系包括对数关系、双曲线关系等。

例3-2 如果认为⼀个国家或地区总产出具有规模报酬不变的特征，那么采⽤⼈均产出y与⼈均资本k的形式，该国家或者说地区的总产出规律可以表⽰为下列C-D⽣产函数形式y Akα=（2.2）也就是⼈均产出是⼈均资本的函数。

能不能⽤两变量线性回归模型分析这种总量⽣产规律？3．计量模型的设定（1）基本形式：y x αβε=++ （2.3）这⾥ε是⼀个随机变量，它的数学期望为0，即（2.3）中的变量y 、x 之间的关系已经是不确定的了。

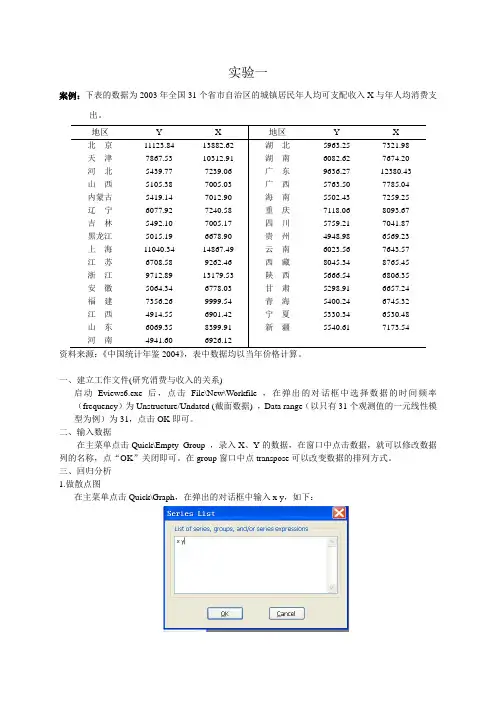
实验一案例：下表的数据为2003年全国31个省市自治区的城镇居民年人均可支配收入X与年人均消费支出。

地区Y X 地区Y X北京11123.84 13882.62 湖北5963.25 7321.98天津7867.53 10312.91 湖南6082.62 7674.20河北5439.77 7239.06 广东9636.27 12380.43山西5105.38 7005.03 广西5763.50 7785.04内蒙古5419.14 7012.90 海南5502.43 7259.25辽宁6077.92 7240.58 重庆7118.06 8093.67吉林5492.10 7005.17 四川5759.21 7041.87黑龙江5015.19 6678.90 贵州4948.98 6569.23上海11040.34 14867.49 云南6023.56 7643.57江苏6708.58 9262.46 西藏8045.34 8765.45浙江9712.89 13179.53 陕西5666.54 6806.35安徽5064.34 6778.03 甘肃5298.91 6657.24福建7356.26 9999.54 青海5400.24 6745.32江西4914.55 6901.42 宁夏5330.34 6530.48山东6069.35 8399.91 新疆5540.61 7173.54河南4941.60 6926.12资料来源：《中国统计年鉴2004》，表中数据均以当年价格计算。

一、建立工作文件(研究消费与收入的关系)启动Eviews6.exe后，点击File\New\Workfile ，在弹出的对话框中选择数据的时间频率（frequency）为Unstructure/Undated (截面数据) ，Data range（以只有31个观测值的一元线性模型为例）为31，点击OK即可。

二、输入数据在主菜单点击Quick\Empty Group ，录入X、Y的数据，在窗口中点击数据，就可以修改数据列的名称，点“OK”关闭即可。

计量经济学eviews实验报告计量经济学Eviews实验报告引言：计量经济学是经济学中的一个重要分支，它通过运用统计学和数学方法来分析经济现象，并建立经济模型来预测和解释经济变量之间的关系。

Eviews是一种流行的计量经济学软件，它提供了丰富的数据分析和模型建立工具，被广泛应用于经济学研究和实证分析。

一、数据收集与处理在进行计量经济学实验之前，首先需要收集相关的经济数据。

这些数据可以来自于各种来源，如经济统计局、金融机构或者自行收集。

然后，我们需要对数据进行处理，包括数据清洗、转换和整理，以便于后续的分析和建模。

二、描述性统计分析描述性统计分析是计量经济学中的第一步，它通过计算数据的均值、方差、相关系数等统计量来描述数据的基本特征。

在Eviews中，我们可以使用各种命令和函数来进行描述性统计分析，比如mean、var、cor等。

通过描述性统计分析，我们可以对数据的分布和变化情况有一个初步的了解。

三、回归分析回归分析是计量经济学中最常用的方法之一，它用于研究一个或多个自变量对一个因变量的影响。

在Eviews中，我们可以使用OLS（Ordinary Least Squares）命令来进行回归分析。

首先，我们需要选择一个合适的回归模型，然后通过最小二乘法估计模型的参数。

通过回归分析，我们可以得到模型的拟合优度、参数估计值和统计显著性等信息，从而判断变量之间的关系和影响程度。

四、模型诊断与改进在进行回归分析之后，我们需要对模型进行诊断和改进。

模型诊断主要包括残差分析、异方差性检验和多重共线性检验等。

在Eviews中，我们可以使用DW （Durbin-Watson）统计量来检验残差的自相关性，使用Breusch-Godfrey检验来检验异方差性，使用VIF（Variance Inflation Factor）来检验多重共线性。

如果模型存在问题，我们可以通过引入其他变量、转换变量或者使用其他的回归方法来改进模型。

⼀元线性回归模型实验报告⼭东轻⼯业学院实验报告成绩课程名称：计量经济学指导教师：刘海鹰实验⽇期： 2012年4⽉9⽇院（系）：商学院专业班级⾦融10-1 实验地点：机电楼B座5楼学⽣姓名：张⽂奇学号： 201008021029 同组⼈⽆实验项⽬名称：⼀元线性回归⽅程的预测⼀、实验⽬的和要求掌握利⽤ EViews 建⽴⼀元线性回归模型的⽅法，并且进⾏参数估计，对其结果进⾏相关分析以及未来形势的预测。

⼆、实验原理⼀元线性回归模型的建⽴与参数估计及点预测、EViews 软件三、主要仪器设备、试剂或材料计算机、EViews 软件四、实验⽅法与步骤1、启动Eviews5软件，建⽴新的workfile.在主菜单中选择【File】--【New】--【Workfile】,弹出Workfile Create对话框，在Workfile structure type中选择Dated-regular frequency，然后在Frequency 中选择annual，Start date中输⼊1980，End date中输⼊1998，点击OK按钮。

2、在主菜单上依次单击Quick→Empty Group。

3、建⽴⼀个空组，输⼊数据。

4、为每个时间序列取序列名。

单击数据表中的SER01，在数据组对话框中的命令窗⼝输⼊该序列名称Y，回车后Yes。

采⽤同样的步骤修改序列名X。

数据输⼊操作完成。

5、数据输⼊完毕，单击⼯作⽂件窗⼝⼯具条的Save或单击菜单兰的File Save将数据存⼊磁盘,⽂件名为张⽂奇。

6、在主菜单上选Quick菜单，单击Estimate Equation项，屏幕出现Equation Specification估计对话框，在Estimation Settings 中选OLS估计，即Least Squares，输⼊：Y C X（其中C为Eviews固定的截距项系数）。

然后OK，出现⽅程窗⼝。

Eviews的估计结果。

一元线性回归分析实验报告.doc一、实验目的本实验旨在通过一元线性回归模型，探讨两个变量之间的关系，即一个变量是否随着另一个变量的变化而呈现线性变化。

通过实际数据进行分析，理解一元线性回归模型的应用及其局限性。

二、实验原理一元线性回归是一种基本的回归分析方法，用于研究两个连续变量之间的关系。

其基本假设是：因变量与自变量之间存在一种线性关系，即因变量的变化可以由自变量的变化来解释。

一元线性回归的数学模型可以表示为：Y = aX + b，其中Y是因变量，X是自变量，a是回归系数，b是截距。

三、实验步骤1.数据收集：收集包含两个变量的数据集，用于建立一元线性回归模型。

2.数据预处理：对数据进行清洗、整理和标准化，确保数据的质量和准确性。

3.绘制散点图：通过散点图观察因变量和自变量之间的关系，初步判断是否为线性关系。

4.建立模型：使用最小二乘法估计回归系数和截距，建立一元线性回归模型。

5.模型评估：通过统计指标（如R²、p值等）对模型进行评估，判断模型的拟合程度和显著性。

6.模型应用：根据实际问题和数据特征，对模型进行解释和应用。

四、实验结果与分析1.数据收集与预处理：我们收集了一个关于工资与工作经验的数据集，其中工资为因变量Y，工作经验为自变量X。

经过数据清洗和标准化处理，得到了50个样本点。

2.散点图绘制：绘制了工资与工作经验的散点图，发现样本点大致呈线性分布，说明工资随着工作经验的变化呈现出一种线性趋势。

3.模型建立：使用最小二乘法估计回归系数和截距，得到一元线性回归模型：Y = 50X + 2000。

其中，a=50表示工作经验每增加1年，工资平均增加50元；b=2000表示当工作经验为0时，工资为2000元。

4.模型评估：通过计算R²值和p值，对模型进行评估。

在本例中，R²值为0.85，说明模型对数据的拟合程度较高；p值为0.01，说明自变量对因变量的影响是显著的。

1.一元线性回归分析（Eviews）研究一个解释变量对一个被解释变量的函数关系Eviews操作主要是Quick。

例子：分析31个省城镇居民平均每人全年家庭总收入X（元）与2011年底城镇居民家庭平1.打开Eviews，依次点击File\New\Workfile。

2.点击”Q uick-Empty Group”,输入数据,点击”obs”,按“”第一列和第二列分别命名为Y和X，将数据粘贴。

二、作Y与X的相关图（散点图）在“Workfile”窗口中，选择X和Y的数据表，双击选择“Open Group”。

选择“View\Graph”，在Graph type中选择“Scatter”，在Fit lines选择“Regression Line”。

从散点图中可以看出，X与Y近似于线性关系，可考虑建立简单线性回归模型。

Y i=β1+β2X i+u i三、估计参数（求出β1和β2的值）假定所建立的模型及其中的随机扰动项u i满足各项古典假定，可以用OLS法估计其参数。

1.方法一：点击“Quick\Estimate Equation”,在Specification中输入“Y C X”。

方法二：在Eviews主命令框中输入“LS Y C X”,按回车。

结果第一行依次表示：变量，参数，标准误差，t统计量，概率值样本回归函数为：Ŷi=11.95802+0.002873X iR2=0.831966,即判定系数表示回归解释平方和与总平方和之比，拟合优度度量值。

2.显示回归结果的图形，在“Equation”框中，点击“Resids”。

四、模型检验1.经济意义检验所估计的参数β̂1=11.95802，β̂2=0.002873，分别表示城镇居民平均每人全年家庭总收入每增加1元，2011年底城镇居民家庭平均每百户计算机拥有量增加0.002873台，与预期的经济意义相符。

2.拟合优度和统计检验R2=0.831966,即判定系数表示回归解释平方和与总平方和之比，拟合优度度量值，说明所建立的模型拟合效果较好。

山西大学实验报告实验报告题目：计量经济学实验报告学院：专业：课程名称：计量经济学学号：学生姓名：教师名称：崔海燕上课时间：一、实验目的：掌握一元线性回归模型的参数估计方法以及对模型的检验和预测的方法。

二、实验原理：1、运用普通最小二乘法进行参数估计；2、对模型进行拟合优度的检验；3、对变量进行显著性检验；4、通过模型对数据进行预测。

三、实验步骤：（一）建立模型1、新建工作文件并保存打开Eviews软件，在主菜单栏点击File\new\workfile，输入start date 1978和end date 2006并点击确认，点击save键，输入文件名进行保存。

2输入并编辑数据在主菜单栏点击Quick键，选择empty\group新建空数据栏，先输入被解释变量名称y，表示中国居民总量消费，后输入解释变量x，表示可支配收入，最后对应各年分别输入数据。

点击name键进行命名，选择默认名称Group01,保存文件。

得到中国居民总量消费支出与收入资料：年份X Y19786678.83806.719797551.64273.219807944.24605.5198184385063.919829235.25482.4198310074.65983.21984115656745.7198511601.77729.2198613036.58210.9198714627.788401988157949560.5198915035.59085.5199016525.99450.9199118939.610375.8199222056.511815.3199325897.313004.7199428783.413944.2199531175.415467.9199633853.717092.5199735956.218080.6199838140.919364.119994027720989.3200042964.622863.92001 46385.4 24370.1 2002 51274 26243.2 2003 57408.1 28035 2004 64623.1 30306.2 2005 74580.4 33214.4 2006 85623.1 36811.2注：y 表示中国居民总量消费 x 表示可支配收入3、 画散点图，判断被解释变量与解释变量之间是否为线性关系在主菜单栏点击Quick\graph 出现对话框，输入 “x y ”，点击确定。

实验二 一元线性回归模型 2.1 实验目的 掌握一元线性回归模型的基本理论，一元线性回归模型的建立、估计、检验及预测的方法，以及相应的EViews软件操作方法。 2.2 实验内容

建立中国消费函数模型。 以表2.1中国的收入与消费的总量数据为基础，建立中国消费函数的一元线性回归模型。 表2.1 年份 X（GDP） Y(Cons) 1990 18319.5 11365.2 1991 21280.4 13145.9 1992 25863.7 15952.1 1993 34500.7 20182.1 1994 46690.7 26796 1995 58510.5 33635 1996 68330.4 40003.9 1997 74894.2 43579.4 1998 79003.3 46405.9 1999 82673.2 49722.8 2000 89112.5 54617.2 2001 98592.9 58927.4 2002 107897.6 62798.5 2003 121730.3 67493.5 2004 142394.2 75439.7

数据来源：2004年中国统计年鉴，中国统计出版社 2.3 实验步骤

2.3.1 散点相关图分析 将表1.1的GDP设为变量X，总消费设为Y，建立变量X和Y的相关图，如图2.1所示。可以看X和Y之间呈现良好的线性关系。可以建立一元线性回归模型。 100002000030000400005000060000700008000004000080000120000160000X

Y

图2.1 2.3.2 估计线性回归模型

在数组窗口中点击Proc\Make Equation，如果不需要重新确定方程中的变量或调整样本区间，可以直接点击OK 进行估计。也可以在EViews 主窗口中点击Quick\Estimate Equation，在弹出的方程设定框（见图2.2）内输入模型： Y C X 或 Y = C(1) + C(2) * X