stata软件基本操作和简单的一元线性回归

STATA软件操作相关与回归分析一、相关分析相关分析用于研究两个变量之间的相关性。

在STATA中，可以使用命令"correlate"进行相关分析。

语法：correlate 变量列表例子：我们以一个示例数据集"auto"为例，研究汽车价格与里程数和马力之间的相关性。

```sysuse autocorrelate price mpg turn```上述命令将计算汽车价格（price）与里程数（mpg）和轮胎转向（turn）之间的相关系数。

输出结果将显示相关系数矩阵，其中包括Pearson相关系数、Spearman相关系数和Kendall相关系数。

二、简单线性回归简单线性回归分析用于研究一个因变量和一个自变量之间的关系。

在STATA中，可以使用命令“regress”进行简单线性回归分析。

语法：regress 因变量自变量例子：我们继续使用上述示例数据集"auto"，研究汽车价格与里程数之间的关系。

```sysuse autoregress price mpg```上述命令将进行汽车价格（price）与里程数（mpg）之间的简单线性回归分析。

输出结果将包括回归系数估计值、拟合优度、标准误差、t值、P值等。

另外，使用命令“predict”可以进行预测。

例子：我们可以使用上述回归模型，对新数据进行价格的预测。

```predict new_price, x```上述命令将对新数据集中的里程数进行预测，并将结果保存在新的变量new_price中。

三、多元回归分析多元回归分析用于研究一个因变量和多个自变量之间的关系。

在STATA中，可以使用命令“regress”进行多元回归分析。

语法：regress 因变量自变量1 自变量2 ...例子：我们使用示例数据集"auto"，研究汽车价格与里程数、马力和重量之间的关系。

```sysuse autoregress price mpg displacement weight```上述命令将进行汽车价格（price）与里程数（mpg）、马力（displacement）和重量（weight）之间的多元线性回归分析。

一元回归的stata实例和stata命令运行结果的存储与调用
在Stata中，我们可以使用`regress`命令进行一元回归分析。

下面是一个示例：
假设我们有一个数据集`data.dta`，包含两个变量`y`和`x`，我们想要使用一元回归来预测`y`，其中`x`是预测变量。

首先，我们需要读取数据集：
```
use data.dta
```
然后，我们可以使用`regress`命令进行一元回归：
```
regress y x
```
运行上述命令后，Stata会输出回归结果，包括截距、斜率和其他统计数据。

现在，我们可以将回归结果存储起来以供后续使用。

我们可以使用`estimates store`命令将回归结果存储到一个特定的名称（例如`reg_results`）：
```
estimates store reg_results
```
存储后，我们可以使用`estimates restore`命令调用回归结果：
```
estimates restore reg_results
```
一旦我们恢复了回归结果，我们可以使用`estimates list`命令查看回归结果：
```
estimates list
```
除了使用`estimates`命令，我们还可以使用返回结果存储在临时或永久变量中。

例如，我们可以使用`predict`命令将预测值存储在一个新变量中：
```
predict y_hat
```
上述命令将回归模型的预测值存储在名为`y_hat`的变量中。

希望以上内容能对你有所帮助！。

stata拟合方程
在Stata中，进行回归分析（拟合方程）是一种常见的统计分析方法。

它可以帮助探索变量之间的关系，并进行预测和推断。

下面介绍如何在Stata中进行回归分析：
1.数据准备：
首先，确保数据已经被加载到Stata中，并且了解想要探索的变量。

2.简单线性回归：
假设想要进行简单线性回归，即一个自变量和一个因变量的关系。

以下是一个示例：
使用regress命令进行简单线性回归
regress y x
这里的y是因变量，x是自变量。

regress命令将拟合一个简单线性回归模型，并输出回归系数、拟合优度、残差等统计信息。

3.多元回归：
如果有多个自变量，可以进行多元回归分析：
使用regress命令进行多元回归
regress y x1 x2 x3
这里x1、x2和x3是多个自变量。

regress命令将拟合一个多元线性回归模型，并输出相关的统计信息。

4.分析结果：
在回归分析完成后，Stata会输出回归系数、拟合优度、标准误差、t值、p 值等统计信息。

这些信息可以帮助理解变量之间的关系、各自的影响力、统计显著性等。

5.可选项和进阶：
●可以使用robust选项来计算鲁棒标准误差。

●可以使用predict命令获取回归结果的预测值、残差等。

●还可以执行其他类型的回归分析，如Logistic回归、Poisson回归等。

Stata提供丰富的选项和功能来进行回归分析，并生成详细的统计摘要。

这些步骤和命令是简单示例，可以根据具体需求和数据特点进行更多的分析和探索。

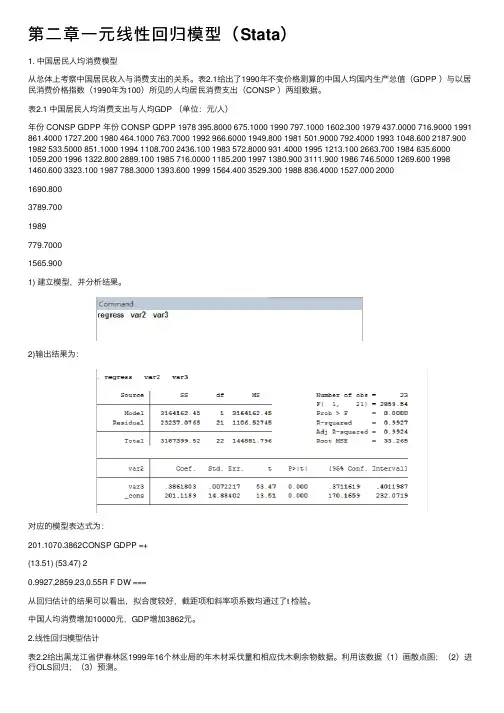
第⼆章⼀元线性回归模型（Stata）1. 中国居民⼈均消费模型从总体上考察中国居民收⼊与消费⽀出的关系。

表2.1给出了1990年不变价格测算的中国⼈均国内⽣产总值（GDPP ）与以居民消费价格指数（1990年为100）所见的⼈均居民消费⽀出（CONSP ）两组数据。

表2.1 中国居民⼈均消费⽀出与⼈均GDP （单位：元/⼈）年份 CONSP GDPP 年份 CONSP GDPP 1978 395.8000 675.1000 1990 797.1000 1602.300 1979 437.0000 716.9000 1991 861.4000 1727.200 1980 464.1000 763.7000 1992 966.6000 1949.800 1981 501.9000 792.4000 1993 1048.600 2187.900 1982 533.5000 851.1000 1994 1108.700 2436.100 1983 572.8000 931.4000 1995 1213.100 2663.700 1984 635.6000 1059.200 1996 1322.800 2889.100 1985 716.0000 1185.200 1997 1380.900 3111.900 1986 746.5000 1269.600 1998 1460.600 3323.100 1987 788.3000 1393.600 1999 1564.400 3529.300 1988 836.4000 1527.000 20001690.8003789.7001989779.70001565.9001) 建⽴模型，并分析结果。

2)输出结果为：对应的模型表达式为：201.1070.3862CONSP GDPP =+(13.51) (53.47) 20.9927,2859.23,0.55R F DW ===从回归估计的结果可以看出，拟合度较好，截距项和斜率项系数均通过了t 检验。