小学奥数：格点型面积(毕克定理)资料讲解

第2讲 格点与面积【知识梳理】一. 正方形格点面积公式（1）定义：在一张纸上，先画出一些水平直线和一些竖直直线，并使任意两条相邻的平行线的距离都相等(通常规定是1个单位)，这样在纸上就形成了一个方格网，其中的每个交点就叫做一个格点．在方格网中，以格点为顶点画出的多边形叫做格点多边形。

（2）公式：右图中的乡村小屋图形就是一个格点多边形．下面就看一下其面积的计算。

用N 表示多边形内部格点，L 表示多边形周界上的格点，S 表示多边形面积，我们能发现如下规律：12L S N =+-．这个规律就是毕克定理。

二、三角形格点问题（1）定义：所谓三角形格点多边形是指：每相邻三点成“∵”或“∴”，所形成的三角形都是等边三角形．规定它的面积为1，以这样的点为顶点画出的多边形为三角形格点多边形。

（2）公式：关于三角形格点多边形的面积同样有它的计算公式：如果用S 表示面积，N 表示图形内包含的格点数，L 表示图形周界上的格点数，那么有22S N L =⨯+-，就是格点多边形面积等于图形内部所包含格点数的2倍与周界上格点数的和减去2。

【典例精讲】【例1】图中每个最小正方形的面积都是1平方厘米，那么三个阴影图形的面积分别是多少平方厘米？【训练1】图中相邻两格点间的距离均为1厘米，那么阴影图形的面积分别为多少平方厘米？【例2】图中每个最小正方形的面积都是1平方厘米，那么阴影图形的面积分别为多少平方厘米？平方厘米？【例3】如图，相邻两格点间的距离均为1厘米，求阴影部分的面积。

【训练3】如图，相邻两格点间的距离均为1厘米，求阴影部分的面积。

米？【训练4】图中每个最小正方形的面积都是4平方厘米，那么阴影图形的面积为多少平方厘米？【能力提升】图中每个最小正方形的面积都是1平方厘米，那么阴影图形的面积为多少平方厘米？【课后巩固】1.图中每个最小正方形的面积都是1平方厘米，那么阴影图形的面积是__________平方厘米。

2.图中每个最小正方形的面积都是1平方厘米，那么阴影图形的面积是___________平方厘米。

1.毕克定理三角形格点面积公式是什么？
答：三角形毕克定理的公式：S=a+b÷2－1。

皮克定理是指一个计算点阵中顶点在格点上的多边形面积公式，其中a表示多边形内部的点数，b表示多边形落在格点边界上的点数，S表示多边形的面积。

三角形是由同一平面内不在同一直线上的三条线段‘首尾’顺次连接所组成的封闭图形，在数学、建筑学有应用。

常见的三角形按边分有普通三角形（三条边都不相等），等腰三角（腰与底不等的等腰三角形、腰与底相等的等腰三角形即等边三角形）；按角分有直角三角形、锐角三角形、钝角三角形等，其中锐角三角形和钝角三角形统称斜三角形。

几何图形题型一：格点图形的面积计算（毕克定理） 1、正方形格点多边形的面积计算公式：（毕克定理）正方形格点多边形的面积＝内点个数＋界点个数÷2－1，如果用S 表示面积，N 表示图形内包含的格点数，L 表示图形周界上的格点数，那么，正方形格点面积可以表示为：S ＝N ＋12L －1。

2、三角形格点多边形及其面积计算公式每相邻三点成“∵”或“∴”，所形成的三角形都是等边三角形，规定它的面积为1，以这样的点为顶点画出的多边形为三角形格点多边形。

三角形格点多边形的面积计算公式：（毕克定理）三角形格点多边形的面积＝(内点个数＋界点个数÷2－1)×2，如果用S 表示面积，N 表示图形内包含的格点数，L 表示图形周界上的格点数，那么，三角形格点面积可以表示为：S ＝(N ＋12L －1)×2。

注意：1．毕克定理对任何格点图形都适用。

要区分面积是几个单位。

2．在数格点时要细心。

3．严格区分正方形格点多边形和三角形格点多边形。

正方形格点图形的面积[模型例题1．]如图是用橡皮筋在钉板上围成的一个三角形，计算它的面积是多少。

(每相邻两个小钉之间的距离都等于1个长度单位)分析 直接套用正方形格点多边形面积公式“正方形格点多边形的面积＝内点个数＋界点个数÷2－1”即可解答。

解：5＋3÷2－1＝5.5 答：三角形的面积为5.5。

[模型例题2．]如图所示，在边长为1厘米的正方形格点中，图形“”的面积是多少平方厘米？分析直接套用正方形格点多边形面积公式“正方形格点多边形的面积＝内点个数＋界点个数÷2－1”即可解答。

解：6＋10÷2－1＝10(平方厘米)答：图形“”的面积是10平方厘米。

三角形格点图形的面积[模型例题3．]下图中有28个点，其中每相邻的三点“∵”或“∴”所形成的三角形都是面积为1的等边三角形，试计算△ABC的面积。

分析直接套用三角形格点多边形面积公式“三角形格点多边形的面积＝(内点个数＋界点个数÷2－1)×2”即可解答。

面积计算公式：皮克公式:格点多边形面积=多边形一周的格点数÷2+多边形内部格点数-1。

设格点多边形的面积为s，它各边上格点的个数和为x。

格点多边形，其内部都只有一个格点，它们的面积与各边上格点的个数和的对应关系如下表，请写出s与x之间的关系式。

相关信息：
1、格点多边形的面积必为整数或半整数（奇数的一半）。

2、格点关于格点的对称点为格点。

3、格点多边形面积公式：设某格点多边形内部有格点a个，格点多边形的边上有格点b个，该格点多边形面积为S，则根据皮克公式有S=a+b/2-1。

4、格点正多边形只能是正方形。

5、格点三角形边界上无其他格点，内部有一个格点，则该点为此三角形的重心。

格点面积公式毕克定理嘿，同学们！今天咱们来聊聊一个挺有趣的数学知识——格点面积公式毕克定理。

先来讲讲我之前遇到的一件小事儿。

有一次我去公园散步，看到地上铺着那种一格一格的地砖，就像咱们数学里的格点图。

我突然就想到了毕克定理，感觉数学知识真是无处不在。

那什么是毕克定理呢？简单来说，就是计算格点多边形面积的一个好办法。

假设一个格点多边形内部有 N 个格点，边上有 L 个格点，那这个多边形的面积就等于 N + L/2 - 1 。

咱们来通过几个例子感受感受。

比如说一个简单的正方形格点图，边长是 3 个格子。

内部没有格点，边上有 4 个格点。

按照毕克定理，面积就是 0 + 4/2 - 1 = 1 ，正好就是这个正方形的面积。

再比如一个稍微复杂点的三角形格点图，内部有 3 个格点，边上有6 个格点。

那它的面积就是 3 + 6/2 - 1 = 5 。

有些同学可能会问了，这毕克定理有啥用呢？用处可大啦！比如说在一些数学竞赛中，如果遇到求格点图形面积的题目，用毕克定理就能快速又准确地得出答案。

而且呀，毕克定理还能帮助我们更好地理解图形和数量之间的关系。

通过计算格点图形的面积，我们能更深入地感受数学的奇妙和规律。

在实际生活中，也能看到毕克定理的影子呢。

比如设计师在设计一些图案的时候，可能就会用到格点和毕克定理来计算面积和比例，确保设计的美观和合理。

同学们，数学的世界就像一个大宝藏，毕克定理只是其中的一颗小宝石。

只要咱们用心去探索，就能发现更多有趣又实用的知识。

就像我在公园里看到的那些地砖格点，它让我在平常的生活中也能想到数学。

咱们学习数学，不只是为了考试，更是为了能在生活中发现它的美，用它来解决问题，让生活变得更有趣、更有条理。

希望大家以后看到格点图形的时候，都能想起毕克定理，用它来算出面积，感受数学的魅力！。

面积计算公式：皮克公式:格点多边形面积=多边形一周的格点数÷2+多边形内部格点数-1
设格点多边形的面积为s，它各边上格点的个数和为x。

格点多边形，其内部都只有一个格点，它们的面积与各边上格点的个数和的对应关系如下表，请写出s与x之间的关系式。

格点的起源
格点问题起源于以下两个问题的研究：
1、狄利克雷除数问题，即求x>1时D2（x）=区域{1≤u≤x，1≤v≤x，uv≤x}上的格点数。

1849年，狄利克雷证明了D2（x）=xlnx+（2ν一1）x+△（x），这里ν为欧拉常数，△（x）=O（x0.5）。

这一问题的目的是要求出使余项估计△（x）=O（x）成立的又的下确界θ0。

2、圆内格点问题，设x>1，A2（x）=圆内μ+ν≤x上的格点数。

高斯证明了A2（x）=πx+R（x），这里R（x）=O（x^1/2）,求使余项估计R（x）=O（x）成立的λ的下确界α的问题，称之为圆内格点问题或高斯圆问题。

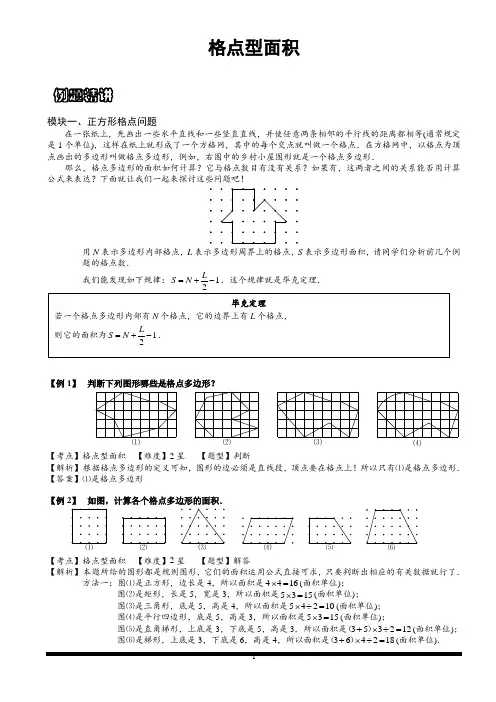
格点型面积模块一、正方形格点问题在一张纸上，先画出一些水平直线和一些竖直直线，并使任意两条相邻的平行线的距离都相等(通常规定是1个单位)，这样在纸上就形成了一个方格网，其中的每个交点就叫做一个格点．在方格网中，以格点为顶点画出的多边形叫做格点多边形，例如，右图中的乡村小屋图形就是一个格点多边形．那么，格点多边形的面积如何计算？它与格点数目有没有关系？如果有，这两者之间的关系能否用计算公式来表达？下面就让我们一起来探讨这些问题吧！用N表示多边形内部格点，L表示多边形周界上的格点，S表示多边形面积，请同学们分析前几个例题的格点数．我们能发现如下规律：12LS N=+-．这个规律就是毕克定理．【例1】判断下列图形哪些是格点多边形？⑴⑵⑶【考点】格点型面积【难度】2星【题型】判断【解析】根据格点多边形的定义可知，图形的边必须是直线段，顶点要在格点上！所以只有⑴是格点多边形．【答案】⑴是格点多边形【例2】如图，计算各个格点多边形的面积．【考点】格点型面积【难度】2星【题型】解答【解析】本题所给的图形都是规则图形，它们的面积运用公式直接可求，只要判断出相应的有关数据就行了．方法一：图⑴是正方形，边长是4，所以面积是4416⨯=(面积单位)；图⑵是矩形，长是5，宽是3，所以面积是5315⨯=(面积单位)；图⑶是三角形，底是5，高是4，所以面积是54210⨯÷=(面积单位)；图⑷是平行四边形，底是5，高是3，所以面积是5315⨯=(面积单位)；图⑸是直角梯形，上底是3，下底是5，高是3，所以面积是353212+⨯÷=（）(面积单位)；图⑹是梯形，上底是3，下底是6，高是4，所以面积是364218+⨯÷=（）(面积单位)．毕克定理若一个格点多边形内部有N个格点，它的边界上有L个格点，则它的面积为12LS N=+-．例题精讲如果两格点之间的距离是2，能利用刚计算的结果说出相应面积么？(教师总结：面积数值均扩大4倍．) 方法二：以上部分图形除了利用各自的面积公式直接求出外，我们还可以从推导它们的面积公式过程中得到启发，即用“割补法”或“扩展法”分别转化成长方形来求．这一种方法很重要，在下面的题目中我们还将使用这种方法！如图⑶，我们利用“扩展法”将其转化，如图所示，从图中易知三角形面积是长方形面积的一半．如图⑷，我们利用“割补法”将其阴影部分面积平移到右边，转化成一个长方形，从中易得平行四边形面积．同理，图⑸、⑹也可利用同样的思想．【答案】图⑴16；图⑵15；图⑶10；图⑷15；图⑸12；图⑹18．【例 3】 如图(a )，计算这个格点多边形的面积．【考点】格点型面积 【难度】2星 【题型】解答 【解析】 方法一(扩展法)．这是个三角形，虽然有三角形面积公式可用，但判断它的底和高却十分困难，只能另想别的办法：这个三角形是处在长是6、宽是4的矩形内，除此之外还有其他三个直角三角形，如下右图(b )，这三个直角三角形面积很容易求出，再用矩形面积减去这三个直角三角形面积，就是所要求的三角形面积．矩形面积是6424⨯=；直角三角形Ⅰ的面积是：6226⨯÷=；直角三角形Ⅱ的面积是：4224⨯÷=；直角三角形Ⅲ面积是4224⨯÷=；所求三角形的面积是2464410-++=（）(面积单位)．方法二(割补法)．将原三角形分割成两个我们方便计算面积的三角形，如(c )图．因此三角形的面积是：52252210⨯÷+⨯÷=(面积单位)．【答案】10【例 4】 右图是一个方格网，计算阴影部分的面积．【考点】格点型面积 【难度】2星 【题型】解答 【关键词】新加坡小学数学奥林匹克竞赛 【解析】 扩展法．把所求三角形扩展成正方形ABCD 中．这个正方形中有四个三角形：一个是要求的AEF V ；另外三个分别是：△ABE 、△FEC 、△DAF ，它们都有一条边是水平放置的，易求它们的面积分别为21.5cm ，22cm ，21.5cm ．所以，图中阴影部分的面积为：33 1.5224⨯-⨯+=（）(2cm )．【答案】4【例 5】 分别计算图中两个格点多边形的面积．【考点】格点型面积 【难度】3星 【题型】解答 【解析】 利用“扩展法”和“割补法”我们都可以简单的得到第一幅图的面积均为9面积单位．第二幅图的面积均为10面积单位．【点评】“一个格点多边形面积的大小很可能是由哪些因素决定呢？”“格点多边形内部的格点数和周界上的格点数与格点多边形的面积有没有什么内在联系呢？”下面我们就来探讨一下！在巩固中，我们发现两个图形面积相等．进一步还可以发现第一个图形边界上的格点数是8个；第二个图形边界上的格点数是10个，包含在图形内的格点数也相等，都是6个．【答案】第一幅图的面积均为9；第二幅图的面积均为10．【巩固】 求下列各个格点多边形的面积．（1） （2） （3） （4）【考点】格点型面积 【难度】3星 【题型】解答【解析】 ⑴ ∵12L =；10N =，∴1211011522L S N =+-=+-=(面积单位)；⑵ ∵10L =；16N =，∴1011612022L S N =+-=+-=(面积单位)；⑶ ∵6L =；12N =，∴611211422L S N =+-=+-=(面积单位)；⑷ ∵10L =；13N =，∴1011311722L S N =+-=+-=(面积单位)．用N 表示多边形内部格点，L 表示多边形周界上的格点，S 表示多边形面积，请同学们分析前几个例题的格点数．我们能发现如下规律：12LS N =+-．这个规律就是毕克定理．【答案】⑴15；⑵ 20；⑶14；⑷17【例 6】 “乡村小屋”的面积是多少？【考点】格点型面积 【难度】3星 【题型】解答【解析】 图形内部格点数9N =；图形边界上的格点数20L = ；根据毕克定理， 则1182LS N =+-=(单位面积)． 【答案】18【例 7】 右图是一个812⨯面积单位的图形．求矩形内的箭形ABCDEFGH 的面积．H GFED C BA【考点】格点型面积 【难度】3星 【题型】解答 【解析】 箭形ABCDEFGH 的面积810214842121232246=+÷-+⨯+÷-⨯=++=（）（）(面积单位)． 【答案】46【例 8】 比较图中的两个阴影部分①和②的面积，它们的大小关系______【考点】格点型面积【难度】3星【题型】填空【关键词】希望杯，五年级，二试，第9题，6分【解析】①的面积为：1112111313222⨯⨯+⨯⨯+⨯⨯=，②的面积也为3223⨯÷=。

第2讲 格点与面积【知识梳理】一. 正方形格点面积公式（1）定义：在一张纸上，先画出一些水平直线和一些竖直直线，并使任意两条相邻的平行线的距离都相等(通常规定是1个单位)，这样在纸上就形成了一个方格网，其中的每个交点就叫做一个格点．在方格网中，以格点为顶点画出的多边形叫做格点多边形。

（2）公式：右图中的乡村小屋图形就是一个格点多边形．下面就看一下其面积的计算。

用N 表示多边形内部格点，L 表示多边形周界上的格点，S 表示多边形面积，我们能发现如下规律：12L S N =+-．这个规律就是毕克定理。

二、三角形格点问题（1）定义：所谓三角形格点多边形是指：每相邻三点成“∵”或“∴”，所形成的三角形都是等边三角形．规定它的面积为1，以这样的点为顶点画出的多边形为三角形格点多边形。

（2）公式：关于三角形格点多边形的面积同样有它的计算公式：如果用S 表示面积，N 表示图形内包含的格点数，L 表示图形周界上的格点数，那么有22S N L =⨯+-，就是格点多边形面积等于图形内部所包含格点数的2倍与周界上格点数的和减去2。

【典例精讲】【例1】图中每个最小正方形的面积都是1平方厘米，那么三个阴影图形的面积分别是多少平方厘米？【答案】4平方厘米；4平方厘米；12平方厘米【解析】左起第一个阴影图形可以分割成4个小正方形，面积为4平方厘米；左起第二个阴影图形可以分割成上、下两个三角形，上面三角形的面积为2×2÷2=2平方厘米，下面三角形的面积是2×2÷2=2平方厘米，则阴影部分的面积为2+2=4平方厘米；左起第三个阴影部分图形可以分割成上面一个三角形、下面一个梯形，上面三角形的面积为5×2÷2=5平方厘米，下面梯形的面积为（2+5）×2÷2=7平方厘米，则阴影部分的面积为5+7=12平方厘米。

【训练1】图中相邻两格点间的距离均为1厘米，那么阴影图形的面积分别为多少平方厘米？【答案】8平方厘米；8平方厘米【解析】左起第一个阴影部分可以分割成8个小正方形，面积为8平方厘米；左起第二个阴影部分可以分割成上、下两个三角形，上面三角形的面积是4×2÷2=4平方厘米，下面三角形的面积为4×2÷2=4平方厘米，则阴影部分的面积为4+4=8平方厘米。

小学奥数：格点型面积（毕克定理）板块一正方形格点问题在一张纸上，先画出一些水平直线和一些竖直直线，并使任意两条相邻的平行线的距离都相等（通常规定是1个单位），这样在纸上就形成了一个方格网，其中的每个交点就叫做一个格点•在方格网中，以格点为顶点画出的多边形叫做格点多边形，例如，右图中的乡村小屋图形就是一个格点多边形.那么，格点多边形的面积如何计算？它与格点数目有没有关系？如果有，这两者之间的关系能否用计算用N表示多边形内部格点，L表示多边形周界上的格点，S表示多边形面积，请同学们分析前几个例题的格点数.我们能发现如下规律：S = N - -1 •这个规律就是毕克定理.2毕克定理若一个格点多边形内部有N个格点，它的边界上有L个格点，则它的面积为s=N +丄一1 •2【例1】用9个钉子钉成相互间隔为1厘米的正方阵（如右图）•如果用一根皮筋将适当的三个钉子连结起来就得到一个三角形，这样得到的三角形中，面积等于1平方厘米的三角形的个数有多少？面积等于2平方厘米的三角形有多少个？【例3】判断下列图形哪些是格点多边形?【巩固】如果两格点之间的距离是2，能利用刚计算的结果说出相应面积么？（教师总结：面积数值均扩大4倍.）【例【例2】如图，4 4的方格纸上放了 __________ 个.【例【例6】（“新加坡小学数学奥林匹克”竞赛试题）右图是一个方格网，计算阴影部分的面积. 【例7】分别计算图中两个格点多边形的面积.【巩固】求下列各个格点多边形的面积.【例8】我们开始提到的“乡村小屋”的面积是多少?⑷【例9】右图是一个8 12面积单位的图形.求矩形内的箭形ABCDEFGH的面积.H【例11】 （“小学数学奥林匹克”竞赛试题）5 5的方格纸，小方格的面积是 1平方厘米，小方格的顶点称为格点.请你在图上选 7个格点，要求其中任意 3个格点都不在一条直线上，并且使这 7个点用直线连接后所围成的面积尽可能大•那么，所围图形的面积是__________ 平方厘米.【例12】 （“保良局亚洲区城市小学数学”竞赛试题 ）第一届保良局亚洲区城市小学数学邀请赛在 7月21日开幕，下面的图形中，每一个小方格的面积是 1 ,那么7、2、1三个数字所占的面积之和是多少？【例13】 （第六届“从小爱数学”邀请赛试题）两个边长相等的正方形各被分成25个大小相同的小方格.现将这两个正方形的一部分重叠起来，若左上角的阴影部分 （块状）面积为5.12cm 2，右下角的阴影部分（线状）面积为7.4cm 2，求大正方形的面积.【例14】 （第六届“华杯赛”试题）图中正六边形 ABCDEF 的面积是54 , AP=2PF , CQ=2BQ ，求阴影四边形CEPQ 的面积.F D【例10】 右图中每个小正方形的面积都是1那么图中这只“狗”所占的面积是多少?板块二三角形格点问题所谓三角形格点多边形是指：每相邻三点成•”或“•••”，所形成的三角形都是等边三角形•规定它的面 积为1，以这样的点为顶点画出的多边形为三角形格点多边形.关于三角形格点多边形的面积同样有它的计算公式：如果用 S 表示面积，N 表示图形内包含的格点数， L 表 示图形周界上的格点数，那么有 S=2 N ，L_2，就是格点多边形面积等于图形内部所包含格点数的 2倍与 周界上格点数的和减去 2.【例15】 如图（a ），有21个点，每相邻三个点成或，所形成的三角形都是等边三角形.计算三角形ABC 的面积.A EF D CB (b)【巩固】如图，每相邻三个点所形成的三角形都是面积为 1的等边三角形，计算 ABC 的面积.【例18】 如图，如果每一个小三角形的面积是 1平方厘米，那么四边形 ABCD 的面积是多少平方厘米?【例16】 （每相邻三个点•”或成面积为 1的等边三角形）.【例17】 把大正三角形每边八等分，组成如右图所示的三角形网•如果大三角形的面积是 粗线所围成的三角形的面积.128,求图中A(a)C 求下列格点多边形的面积 ⑴ ⑵⑶ ⑷【例19】 把同一个三角形的三条边分别 5等分、7等分（如图1，图2），然后适当连接这些等分点，便得至厅若干个面积相等的小三角形•已知图 1中阴影部分面积是 294平方分米，那么图 2中阴影部分的面积是 ______ 方分米.【例20】 将图中的图形分割成面积相等的三块.【例22】 （第五届“华杯赛”试题）正六边形ABCDEF 的面积是6平方厘米.M 是AB 中点，N 是CD 中点，P 是EF 中点.问：三角形 MNP 的面积是多少平方厘米？【例23】 如果下图中任意相邻的三个点构成的三角形面积都是 ____ 方厘米.NNE【例21】 如图涂阴影部分的小正六角星形面积是 16平方厘米，问：大正六角星形面积是多少平方厘米?2平方厘米•那么，三角形 ABC 的面积是團I 2。