【精准解析】上海市七宝中学2019-2020学年高二下学期期中考试数学试题

2019-2020学年高二第二学期期中数学试卷一、选择题（共10小题）.1．（x +1）n 的展开式共有11项，则n 等于（ ） A ．9B ．10C ．11D ．82．已知函数f （x ）＝sin x ，其导函数为f '（x ），则f '（π3）＝（ ）A ．−12B ．32C ．12D ．−323．从0，1，2，3这四个数中任取两个不同的数组成一个两位数，则这个两位数是偶数的概率为（ ） A ．13B ．49C ．12D ．594．在（x +2）5的展开式中，二项式系数的最大值为（ ） A ．5B ．15C ．10D ．205．已知正态密度曲线的函数关系式是f （x ）=2πσe (x−μ)22σ2，设有一正态总体，它的概率密度曲线是函数f （x ）的图象，且f （x ）=18πe (x−10)28（x ∈R ），则这个正态总体的平均数μ与标准差σ分别是（ ） A ．10与8 B ．10与2C ．8与10D ．2与106．设n ∈N*，则Cn01n 80+Cn11n ﹣181+C n21n ﹣282+C n31n ﹣383+……+C nn−1118n ﹣1+Cnn 108n 除以9的余数为（ ）A ．0B ．8C ．7D ．27．在比赛中，如果运动员甲胜运动员乙的概率是23，那么在五次比赛中，运动员甲恰有三次获胜的概率是（ ）A．40243B．80243C．110243D．202438．设（1+x）n＝a0+a1x+a2x2+a3x3+……+a n x n，若a0+a1+a2+a3+……+a n＝64，则展开式中系数最大的项是（）A．15x2B．21x3C．20x3D．30x39．某旅游公司为了推出新的旅游产品项目，派出五名工作人员前往重庆的三个网红景点一“洪崖洞夜景、轻轨穿楼、长江索道”进行团队游的可行性调研．若每名工作人员只去一个景点，每个景点至少有一名工作人员前往，其中工作员甲、乙需要到同一景点调研，则不同的人员分配方案种数为（）A．18 B．36 C．54 D．7210．设函数f(x)=ax+xx−1(x＞1)，若a是从1，2，3三数中任取一个，b是从2，3，4，5四数中任取一个，那么f（x）＞b恒成立的概率为（）A．16B．14C．34D．56二、多项选择题（本大题共2小题，每小题5分，共10分.全部选对得5分，部分选对得3分，有选错得0分）11．若随机变量X服从两点分布，其中P(X=0)=13，E（X）、D（X）分别为随机变量X均值与方差，则下列结论正确的是（）A．P（X＝1）＝E（X）B．E（3X+2）＝4C．D（3X+2）＝4 D．D(X)=4912．已知函数f（x）＝xlnx，若0＜x1＜x2，则下列结论正确的是（）A．x2f（x1）＜x1f（x2）B．x1+f（x1）＜x2+f（x2）C ．f(x 1)−f(x 2)x 1−x 2＜0D ．当lnx ＞﹣1时，x 1f （x 1）+x 2f （x 2）＞2x 2f （x 1） 三、填空题（本大题共4小题，每小题5分，共20分） 13．函数在f （x ）＝﹣x +1x在[1，2]上的最大值是 ．14．随机变量ξ服从正态分布N （1，σ2），已知P （ξ＜0）＝0.3，则P （ξ＜2）＝ ．15．设（1+ax ）2020＝a 0+a 1x +a 2x 2+……+a 2019x 2019+a 2020x 2020，若a 1+2a 2+3a 3+…+2019a 2019+2020a 2020＝2020a ，则实数a ＝ ．16．在《爸爸去哪儿》第二季第四期中，村长给6位“萌娃”布置一项搜寻空投食物的任务．已知：①食物投掷地点有远、近两处；②由于Grace 年纪尚小，所以要么不参与该项任务，但此时另需一位小孩在大本营陪同，要么参与搜寻近处投掷点的食物；③所有参与搜寻任务的小孩须被均分成两组，一组去远处，一组去近处，那么不同的搜寻方案有 种．（以数字作答）四、解答题（本大题共6小题，共计70分） 17．有4名学生和2位老师站成一排合影． （1）若2位老师相邻，则排法种数为多少？ （2）若2位老师不相邻，则排法种数为多少？18．甲、乙、丙三位学生各自独立地解同一道题，已知甲、乙做对该题的概率都为13，丙做对该题的概率为14，且三位学生能否做对相互独立，设随机变量X 表示这三位学生中做对该题的人数，其分布列为：X0123P13a b136（1）求a，b的值；（2）求X的数学期望．19．在（x+2）10的展开式中，求：（1）含x8项的系数；（2）如果第3r项和第r+2项的二项式系数相等，求r的值，20．在一次购物抽奖活动中，假设10张奖券中有一等奖奖券1张，可获价值50元的奖品，有二等奖奖券3张，每张可获价值10元的奖品，其余6张没有奖品．（1）顾客甲从10张奖券中任意抽取1张，求中奖次数X的概率分布．（2）顾客乙从10张奖券中任意抽取2张，①求顾客乙中奖的概率；②设顾客乙获得的奖品总价值Y元，求Y的概率分布及期望．21．2018年10月28日，重庆公交车坠江事件震惊全国，也引发了广大群众的思考﹣﹣如何做一个文明的乘客．全国各地大部分社区组织居民学习了文明乘车规范．A社区委员会针对居民的学习结果进行了相关的问卷调查，并将得到的分数整理成如图所示的统计图．（Ⅰ）求得分在[70，80）上的频率；（Ⅱ）求A社区居民问卷调査的平均得分的估计值；（同一组中的数据以这组数据所在区间中点的值作代表）（Ⅲ）由于部分居民认为此项学习不具有必要性，A社区委员会对社区居民的学习态度作调查，所得结果统计如下：（表中数据单位：人）认为此项学习十分必要认为此项学习不必要50岁以上400600 50岁及50岁以下800200根据上述数据，计算是否有99.9%的把握认为居民的学习态度与年龄相关．附：K2=n(ad−bc)2(a+b)(c+d)(a+c)(b+d)，其中n＝a+b+c+d．P（K2≥k0）0.1000.0500.0100.001 k0 2.706 3.841 6.63510.82822．已知函数f（x）＝（ax2+x+a）e﹣x（a∈R）．（Ⅰ）当a＝0时，求f（x）在点（0，f（0））处的切线方程；（Ⅱ）若a≥0，求函数f（x）的单调区间；（Ⅲ）若对任意的a≤0，f（x）≤bln（x+1）在x∈[0，+∞）上恒成立，求实数b的取值范围．参考答案一、单项选择题（本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的.）1．（x+1）n的展开式共有11项，则n等于（）A．9 B．10 C．11 D．8【分析】直接利用二项式定理的性质写出结果即可．解：因为（x+1）n的展开式共有11项，则n+1＝11⇒n＝10；故选：B．【点评】本题考查二项式定理的简单性质的应用，基本知识的考查．2．已知函数f（x）＝sin x，其导函数为f'（x），则f'（π3）＝（）A．−12B．32C．12D．−32【分析】可以求出导函数f′（x）＝cos x，从而可得出f′(π3)的值．解：∵f（x）＝sin x，∴f′（x）＝cos x，∴f′(π3)=cosπ3=12．故选：C．【点评】本题考查了基本初等函数的求导公式，已知函数求值的方法，考查了计算能力，属于基础题．3．从0，1，2，3这四个数中任取两个不同的数组成一个两位数，则这个两位数是偶数的概率为（）A．13B．49C．12D．59【分析】基本事件总数n＝3×3＝9，这个两位数是偶数包含的基本事件个数m＝1×3+1×2＝5．由此能求出这个两位数是偶数的概率．解：从0，1，2，3这四个数中任取两个不同的数组成一个两位数，基本事件总数n＝3×3＝9，这个两位数是偶数包含的基本事件个数m＝1×3+1×2＝5．∴这个两位数是偶数的概率为p=mn=59．故选：D．【点评】本题主要考查概率的求法，考查古典概型计算公式等知识，意在考查学生的转化能力和计算求解能力．4．在（x+2）5的展开式中，二项式系数的最大值为（）A．5 B．15 C．10 D．20【分析】展开式中共有6项，根据展开式中间两项的二项式系数最大，故第3，4项的二项式系数最大，问题得以解决．解：展开式中共有6项，根据展开式中间两项的二项式系数最大故第3，4项的二项式系数最大，故C52＝C53＝10，故选：C．【点评】本题主要考查二项式系数的性质及二项展开式的通项公式是解决二项展开式的特定项问题的工具，属于基础题． 5．已知正态密度曲线的函数关系式是f （x ）=2πσe (x−μ)22σ2，设有一正态总体，它的概率密度曲线是函数f （x ）的图象，且f （x ）=8πe (x−10)28（x ∈R ），则这个正态总体的平均数μ与标准差σ分别是（ ） A ．10与8B ．10与2C ．8与10D ．2与10【分析】把已知函数解析式转化为正态密度曲线的函数关系式求解．解：∵f （x ）=18πe (x−10)28=22π(x−10)22×22，∴平均数μ＝10，标准差σ＝2． 故选：B ．【点评】本题考查正态密度曲线的函数，是基础题． 6．设n ∈N*，则Cn 01n 80+C n 11n ﹣181+C n 21n ﹣282+C n 31n ﹣383+……+C nn−1118n ﹣1+Cnn 108n 除以9的余数为（ ）A ．0B ．8C ．7D ．2【分析】直接利用二项式定理把条件转化即可求解结论． 解：因为Cn 01n 80+C n 11n ﹣181+C n 21n ﹣282+C n 31n ﹣383+……+C nn−1118n ﹣1+Cnn 108n ＝（1+8）n ＝9n ； 故除以9的余数为0； 故选：A ．【点评】本题考查余数的求法，是中档题，解题时要认真审题，注意组合数性质及二项式定理的合理运用．7．在比赛中，如果运动员甲胜运动员乙的概率是23，那么在五次比赛中，运动员甲恰有三次获胜的概率是（ ） A ．40243B ．80243C ．110243D ．20243【分析】由条件利用n 次独立重复实验中恰好发生k 次的概率计算公式，计算求得结果． 解：根据每次比赛中，甲胜运动员乙的概率是23，故在五次比赛中，运动员甲恰有三次获胜的概率是C 53•(23)3•(1−23)2=80243， 故选：B ．【点评】本题主要考查n 次独立重复实验中恰好发生k 次的概率计算公式，属于基础题． 8．设（1+x ）n ＝a 0+a 1x +a 2x 2+a 3x 3+……+a n x n ，若a 0+a 1+a 2+a 3+……+a n ＝64，则展开式中系数最大的项是（ ） A ．15x 2B ．21x 3C ．20x 3D ．30x 3【分析】由题意可得 a 0+a 1+a 2+…+a n ＝（1+1）n ＝64，得 n ＝6，由此求得展开式中系数最大的项．解：因为 a 0+a 1+a 2+…+a n ＝（1+1）n ＝64，得 n ＝6， 故展开式中系数最大的项是第四项；即∁63x 3＝20x 3；故选：C ．【点评】本题主要考查二项式定理的应用，二项式系数的性质，属于中档题． 9．某旅游公司为了推出新的旅游产品项目，派出五名工作人员前往重庆的三个网红景点一“洪崖洞夜景、轻轨穿楼、长江索道”进行团队游的可行性调研．若每名工作人员只去一个景点，每个景点至少有一名工作人员前往，其中工作员甲、乙需要到同一景点调研，则不同的人员分配方案种数为（ ） A ．18B ．36C ．54D ．72【分析】根据分步计数原理，把2元素组合一个复合元素，再进行组合和分配，问题得以解决．解：由于工作员甲、乙需要到同一景点调研，把A，B看作一个复合元素，则本题等价于4个元素分配到3个位置，每一个位置至少一个，故有C42A33＝36种，故选：B．【点评】本题考查了排列组合混合问题，先选后排是最基本的思想．10．设函数f(x)=ax+xx−1(x＞1)，若a是从1，2，3三数中任取一个，b是从2，3，4，5四数中任取一个，那么f（x）＞b恒成立的概率为（）A．16B．14C．34D．56【分析】先把f（x）的解析式变形，用分离常数法，然后用均值不等式求出最小值，本题是一个古典概型，试验发生包含的所有事件是12个，满足条件的事件是10个，列举出结果．解：x＞1，a＞0，f（x）＝ax+x−1+1x−1=ax+1x−1+1＝a（x﹣1）+1x−1+1+a≥2√a+1+a＝（√a+1）2，当且仅当x=√1a+1＞1时，取“＝”，∴f（x）min＝（√a+1）2，于是f（x）＞b恒成立就转化为（√a+1）2＞b成立．设事件A：“f（x）＞b恒成立”，则基本事件总数为12个，即（1，2），（1，3），（1，4），（1，5）；（2，2），（2，3），（2，4），（2，5）；（3，2），（3，3），（3，4），（3，5）；事件A包含事件：（1，2），（1，3）；（2，2），（2，3），（2，4），（2，5）；（3，2），（3，3），（3，4），（3，5）共10个由古典概型得P（A）=1012=56，故选：D．【点评】在使用古典概型的概率公式时，应该注意：（1）要判断该概率模型是不是古典概型；（2）要找出随机事件A包含的基本事件的个数和试验中基本事件的总数；当解析式中含有分式，且分子分母是齐次的，注意运用分离常数法来进行式子的变形，在使用均值不等式应注意一定，二正，三相等．二、多项选择题（本大题共2小题，每小题5分，共10分.全部选对得5分，部分选对得3分，有选错得0分）11．若随机变量X服从两点分布，其中P(X=0)=13，E（X）、D（X）分别为随机变量X均值与方差，则下列结论正确的是（）A．P（X＝1）＝E（X）B．E（3X+2）＝4C．D（3X+2）＝4 D．D(X)=49【分析】推丑陋同P（X＝1）=23从而E（X）=0×13+1×23=23，D（X）＝（0−23）2×13+（1−23）2×23=29，由此能过河卒子同结果．解：随机变量X服从两点分布，其中P(X=0)=13，∴P（X＝1）=23，E （X ）=0×13+1×23=23，D （X ）＝（0−23）2×13+（1−23）2×23=29，在A 中，P （X ＝1）＝E （X ），故A 正确；在B 中，E （3X +2）＝3E （X ）+2＝3×23+2=4，故B 正确；在C 中，D （3X +2）＝9D （X ）＝9×29=2，故C 错误； 在D 中，D （X ）=29，故D 错误． 故选：AB ．【点评】本题考查命题真假的判断，考查离散型随机变量的分布列、数学期望、方差等基础知识，考查运算求解能力，是中档题．12．已知函数f （x ）＝xlnx ，若0＜x 1＜x 2，则下列结论正确的是（ ） A ．x 2f （x 1）＜x 1f （x 2）B ．x 1+f （x 1）＜x 2+f （x 2）C ．f(x 1)−f(x 2)x 1−x 2＜0D ．当lnx ＞﹣1时，x 1f （x 1）+x 2f （x 2）＞2x 2f （x 1）【分析】根据条件分别构造不同的函数，求函数的导数，利用函数单调性和导数之间的关系进行判断即可． 解：A ．正确；因为令g （x ）=f(x)x=lnx ，在（0，+∞）上是增函数，∴当 0＜x 1＜x 2 时，g （x 1）＜g （x 2），∴f(x 1)x 1＜f(x 2)x 2即x 2f （x 1）＜x 1f （x 2）．B ．错误；因为令g （x ）＝f （x ）+x ＝xlnx +x ∴g ′（x ）＝lnx +2，∴x ∈（e ﹣2，+∞）时，g ′（x ）＞0，g （x ）单调递增，x ∈（0，e ﹣2）时，g ′（x ）＜0，g （x ）单调递减．∴x 1+f （x 1）与x 2+f （x 2）无法比较大小．C ．错误；因为令g （x ）＝f （x ）﹣x ＝xlnx ﹣x ，g ′（x ）＝lnx ，∴x ∈（0，1）时，g ′（x ）＜0，g （x ）在（0，1）单调递减，x ∈（1，+∞）时，g ′（x ）＞0，g （x ）在（1，+∞）单调递增，∴当0＜x 1＜x 2＜1时，g （x 1）＞g （x 2）， ∴f （x 1）﹣x 1＞f （x 2）﹣x 2， ∴f （x 1）﹣f （x 2）＞x 1﹣x 2， ∴f(x 1)−f(x 2)x 1−x 2＜0．当1＜x 1＜x 2 时，g （x 1）＜g （x 2） ∴f （x 1）﹣x 1＜f （x 2）﹣x 2， ∴f （x 1）﹣f （x 2）＜x 1﹣x 2， ∴f(x 1)−f(x 2)x 1−x 2＞0．D．正确；因为lnx＞﹣1时，f（x）单调递增，又∵A正确，∴x1•f（x1）+x2•f（x2）﹣2x2f（x1）＞x1[f（x1）﹣f（x2）]+x2[f（x2）﹣f（x1）]＝（x1﹣x2）[f（x1）﹣f（x2）]＞0．故选：AD．【点评】本题主要考查命题的真假判断，在求解中用到了利用导数判断函数的单调性，并用到了函数单调性的定义．需要学习掌握的是构造函数的办法，综合性较强，有一定的难度．三、填空题（本大题共4小题，每小题5分，共20分）在[1，2]上的最大值是0 ．13．函数在f（x）＝﹣x+1x【分析】先求导数，得单调性，进而得出最大值．＜0，解：因为f′（x）＝﹣1−1x2所以f（x）在[1，2]上单调递减，f（x）max＝f（1）＝﹣1+1＝0，故答案为：0．【点评】本题考查利用导数求单调性进而得出最大值．14．随机变量ξ服从正态分布N（1，σ2），已知P（ξ＜0）＝0.3，则P（ξ＜2）＝0.7 ．【分析】随机变量ξ服从正态分布N（1，σ2），得到曲线关于x＝1对称，根据曲线的对称性得到小于0的和大于2的概率是相等的，从而做出大于2的数据的概率，根据概率的性质得到结果．解：随机变量ξ服从正态分布N（1，σ2），∴曲线关于x＝1对称，∴P（ξ＜0）＝P（ξ＞2）＝0.3，∴P（ξ＜2）＝1﹣0.3＝0.7，故答案为：0.7【点评】本题考查正态分布曲线的特点及曲线所表示的意义，考查概率的性质，是一个基础题，这种题目可以出现在选择或填空中，是一个送分题目．15．设（1+ax）2020＝a0+a1x+a2x2+……+a2019x2019+a2020x2020，若a1+2a2+3a3+…+2019a2019+2020a2020＝2020a，则实数a＝0 ．【分析】结合所求式子与已知的式子特点，可以对原函数求导数，然后利用赋值法求解即可．解：对已知的式子两边同时求导数可得：2020a（1+ax）2019=a1+2a2x+3a3x2+⋯+2020a2020x2019，令x＝1则：2020a（1+ax）2019＝a1+2a2+3a3+…+2020a2020，又因为：a1+2a2+3a3+…+2019a2019+2020a2020＝2020a，所以（1+a）2019＝1，所以a＝0．故答案为：0．【点评】本题考查二项式定理的系数的性质、赋值法的应用．同时考查了学生的运算能力，属于基础题．16．在《爸爸去哪儿》第二季第四期中，村长给6位“萌娃”布置一项搜寻空投食物的任务．已知：①食物投掷地点有远、近两处；②由于Grace年纪尚小，所以要么不参与该项任务，但此时另需一位小孩在大本营陪同，要么参与搜寻近处投掷点的食物；③所有参与搜寻任务的小孩须被均分成两组，一组去远处，一组去近处，那么不同的搜寻方案有 40 种．（以数字作答）【分析】根据题意，分2种情况讨论：①、Grace 不参与该项任务，需一位小孩在大本营陪同，则其余4人被均分成两组，一组去远处，一组去近处；②、Grace 参与该项任务，则从其余5人中选2人去近处，剩余3人搜寻远处，分别求出每种情况的方案数目；由分类计数原理计算可得答案． 解：根据题意，分2种情况讨论： ①、Grace 不参与该项任务，在其余5人中，任选1人在大本营陪同，有C 51＝5种情况， 剩余4人，平均分成2组，有C 42C 22A 22=3种分组方法，在将2组对应2个地点，有A 22＝2种情况，此时一共有5×3×2＝30种方案； ②、Grace 参与该项任务，在其余5人中，任选2人与Grace 一起搜寻近处投掷点的食物，有C 52＝10种情况， 而剩余3人搜寻远处投掷点的食物，有1种情况， 则此时一共有10×1＝10种方案；则一共有30+10＝40种符合题意的分配方案； 故答案为：40．【点评】本题考查排列、组合的运用，要先认真分析题意，注意2种方案参与的人数不同．四、解答题（本大题共6小题，共计70分） 17．有4名学生和2位老师站成一排合影．（1）若2位老师相邻，则排法种数为多少？（2）若2位老师不相邻，则排法种数为多少？【分析】（1）2位老师站在一起，可以采取绑定法计数，先绑定2位老师，再将2者看作一人与4名学生进行全排列；（2）2位老师互不相邻，可先排4名学生，然后把2位老师插空，最后用乘法原理计数．解：（1）先把2位老师“捆绑”看做1元素，与其余4个元素进行排列，再对2位老师进行排列，共有A22A55＝240种，（2）先让4名学生站好，有A44种排法，这时有5个“空隙”可供2位老师选取，共有A44A52＝480种．【点评】本题考查排列、组合及简单计数问题，解题的关键是熟练掌握计数原理及排列组合的公式，掌握一些特殊的计数技巧，如本题中绑定法，插空法．要注意每种方法与相应问题的对应．18．甲、乙、丙三位学生各自独立地解同一道题，已知甲、乙做对该题的概率都为13，丙做对该题的概率为14，且三位学生能否做对相互独立，设随机变量X表示这三位学生中做对该题的人数，其分布列为：X0123P13a b136（1）求a，b的值；（2）求X的数学期望．【分析】（1）利用相互独立事件概率乘法公式和互斥事件概率加法公式能求出a，利用对立事件概率计算公式能求出b．（2）由离散型随机变量的分布列能求出数学期望E（X）．解：（1）∵甲、乙做对该题的概率都为13，丙做对该题的概率为14，且三位学生能否做对相互独立， ∴a =13×(1−13)×(1−14)+(1−13)×13×(1−14)+(1−13)×(1−13)×14=49， b ＝1﹣P （X ＝0）﹣P （X ＝1）﹣P （X ＝3）＝1−13−49−136=736．（2）E （X ）=0×13+1×49+2×736+3×136=1112． 【点评】本题考查概率的求法，考查离离散型随机变量的数学期望的求法，考查相互独立事件概率乘法公式、互斥事件概率加法公式、对立事件概率计算公式等基础知识，考查运算求解能力，是中档题． 19．在（x +2）10的展开式中，求： （1）含x 8项的系数；（2）如果第3r 项和第r +2项的二项式系数相等，求r 的值， 【分析】先求出展开式的通项．（1）令通项中x 的指数为8，求出k 的值即可； （2）写出该两项的二项式系数，令其相等，求出r 的值． 解：（1）二项式展开式的通项如下：T r+1=C 10r 2r x 10−r ，由已知令10﹣r ＝8， 所以r ＝2．所以含x 8项的系数为C 10222=180．（2）第3r 项与第r +2项的二项式系数相等， 则C 103r−1=C 10r+1，即3r ﹣1＝r +1或3r ﹣1+r +1＝10． 解得r ＝1或r =52（舍）．故r 的值为1．【点评】本题考查二项式展开式系数的性质，利用通项法研究特定项的问题，同时考查学生的化简运算能力．属于基础题．20．在一次购物抽奖活动中，假设10张奖券中有一等奖奖券1张，可获价值50元的奖品，有二等奖奖券3张，每张可获价值10元的奖品，其余6张没有奖品． （1）顾客甲从10张奖券中任意抽取1张，求中奖次数X 的概率分布． （2）顾客乙从10张奖券中任意抽取2张， ①求顾客乙中奖的概率；②设顾客乙获得的奖品总价值Y 元，求Y 的概率分布及期望．【分析】（1）抽奖一次，只有中奖和不中奖两种情况，1表示中奖，0表示不中奖，则X 的取值只有0，1两种，分别求出相应的概率，由此能求出X 的分布列．（2）①顾客乙中奖可分为互斥的两类：所抽取的2张奖券有1张中奖和2张都中奖，由此利用互斥事件概率加法公式能求出顾客乙中奖的概率．②顾客乙所抽取的2张奖券中有0张中奖，1张中奖（1张1等奖或1张2等奖）或2张都中奖（2张二等奖或2张1等奖或1张2等奖1张2等奖），Y 的可能取值为0，10，20，50，60，分别求出相应的概率，由此能求出随机变量Y 的概率分布列和数学期望．解：（1）抽奖一次，只有中奖和不中奖两种情况， 1表示中奖，0表示不中奖，则X 的取值只有0，1两种，P （X ＝0）=C 61C 101=35，P （X ＝1）=C 41C 101=25，∴X 的分布列为：X1P3525（2）①顾客乙中奖可分为互斥的两类：所抽取的2张奖券有1张中奖和2张都中奖， ∴顾客乙中奖的概率为：P =C 41C 61+C 42C 102=23．②顾客乙所抽取的2张奖券中有0张中奖，1张中奖（1张1等奖或1张2等奖）或2张都中奖（2张二等奖或2张1等奖或1张2等奖1张2等奖）， ∴Y 的可能取值为0，10，20，50，60，P （Y ＝0）=C 62C 102=13， P （Y ＝10）=C 41C 61C 102=25，P （Y ＝20）=C 32C 102=115， P （Y ＝50）=C 11C 61C 102=215， P （Y ＝60）=C 11C 31C 102=115，∴随机变量Y 的概率分布列为：Y 010205060P1325115215115EY =0×13+10×25+20×115+50×215+60×115=16（元）．【点评】本题考查概率的求法，考查离离散型随机变量的数学期望的求法，考查互斥事件概率加法公式、古典概型等基础知识，考查运算求解能力，是中档题．21．2018年10月28日，重庆公交车坠江事件震惊全国，也引发了广大群众的思考﹣﹣如何做一个文明的乘客．全国各地大部分社区组织居民学习了文明乘车规范．A 社区委员会针对居民的学习结果进行了相关的问卷调查，并将得到的分数整理成如图所示的统计图．（Ⅰ）求得分在[70，80）上的频率；（Ⅱ）求A社区居民问卷调査的平均得分的估计值；（同一组中的数据以这组数据所在区间中点的值作代表）（Ⅲ）由于部分居民认为此项学习不具有必要性，A社区委员会对社区居民的学习态度作调查，所得结果统计如下：（表中数据单位：人）认为此项学习十分必要认为此项学习不必要50岁以上400600 50岁及50岁以下800200根据上述数据，计算是否有99.9%的把握认为居民的学习态度与年龄相关．附：K2=n(ad−bc)2(a+b)(c+d)(a+c)(b+d)，其中n＝a+b+c+d．P（K2≥k0）0.1000.0500.0100.001 k0 2.706 3.841 6.63510.828【分析】（Ⅰ）由频率分布直方图计算所求的频率值；（Ⅱ）利用各组的中间值与对应的频率乘积的和，计算平均分；（Ⅲ）根据2×2列联表计算观测值，对照临界值得出结论．解：（Ⅰ）由频率分布直方图，计算得分在[70，80）上的频率为1﹣0.1﹣0.15﹣0.2﹣0.15﹣0.1＝0.3；（Ⅱ）由（Ⅰ）知各组的中间值与对应的频率如下表，中间值455565758595频率0.10.150.20.30.150.1计算问卷调査的平均得分为45×0.1+55×0.15+65×0.2+75×0.3+85×0.15+95×0.1＝70.5；（Ⅲ）根据2×2列联表，认为此项学习十分必要认为此项学习不必要合计50岁以上400600100050岁及50岁以下8002001000总计12008002000计算K2=2000×(400×200−600×800)21000×1000×1200×800≈333.333＞10.828，所以有99.9%的把握认为居民的学习态度与年龄相关．【点评】本题考查了频率分布直方图和样本数字特征的应用问题，也考查了独立性检验的应用问题，是基础题．22．已知函数f（x）＝（ax2+x+a）e﹣x（a∈一、选择题）．（Ⅰ）当a＝0时，求f（x）在点（0，f（0））处的切线方程；（Ⅱ）若a≥0，求函数f（x）的单调区间；（Ⅲ）若对任意的a≤0，f（x）≤bln（x+1）在x∈[0，+∞）上恒成立，求实数b的取值范围．【分析】（Ⅰ）当a＝0时，f（x）＝x•e﹣x，f′（x）＝e﹣x﹣x•e﹣x＝e﹣x（1﹣x），可得f′（0）＝1，f（0）＝0，即可得出切线方程．（Ⅱ）由题意，f'（x）＝（2ax+1）e﹣x﹣（ax2+x+a）e﹣x＝﹣e﹣x[ax2+（1﹣2a）x+a ﹣1]＝﹣e﹣x（x﹣1）（ax+1﹣a）．对a分类讨论：a＝0，a＞0，即可得出．（Ⅲ）令g（a）＝e﹣x（x2+1）a+xe﹣x，a∈（﹣∞，0]，当x∈[0，+∞）时，e﹣x（x2+1）≥0，g（a）单调递增，则g(a)max=g(0)=xe−x．可得g（a）≤bln（x+1）对∀a ∈（﹣∞，0]恒成立等价于bln（x+1）≥g（a）max＝g（0），即xe﹣x≤bln（x+1），对x∈[0，+∞）恒成立，对b分类讨论，利用单调性即可得出．解：（Ⅰ）当a＝0时，f（x）＝x•e﹣x，∴f′（x）＝e﹣x﹣x•e﹣x＝e﹣x（1﹣x）……（1分）∴f′（0）＝1，f（0）＝0，∴函数f（x）在点（0，f（0））处的切线方程为y＝x．……（Ⅱ）由题意，f'（x）＝（2ax+1）e﹣x﹣（ax2+x+a）e﹣x＝﹣e﹣x[ax2+（1﹣2a）x+a ﹣1]＝﹣e﹣x（x﹣1）（ax+1﹣a）．……（ⅰ）当a＝0时，f'（x）＝﹣e﹣x（x﹣1），令f'（x）＞0，得x＜1；f'（x）＜0，得x＞1，所以f（x）在（﹣∞，1）单调递增，（1，+∞）单调递减；……（ⅱ）当a＞0时，1−1a＜1，令f'（x）＞0，得1−1a ＜x＜1；f'（x）＜0，得x＜1−1a或x＞1，……所以f（x）在(1−1a ，1)单调递增，在(−∞，1−1a)，（1，+∞）单调递减，………（Ⅲ）令g（a）＝e﹣x（x2+1）a+xe﹣x，a∈（﹣∞，0]，当x∈[0，+∞）时，e﹣x（x2+1）≥0，g（a）单调递增，则g(a)max=g(0)=xe−x，………………则g（a）≤bln（x+1）对∀a∈（﹣∞，0]恒成立等价于bln（x+1）≥g（a）max＝g （0），即xe﹣x≤bln（x+1），对x∈[0，+∞）恒成立．………（ⅰ）当b≤0时，∀x∈（0，+∞），bln（x+1）＜0，xe﹣x＞0，此时xe﹣x＞bln（x+1），不合题意，舍去．…………（ⅱ）当b＞0时，令h（x）＝bln（x+1）﹣xe﹣x，x∈[0，+∞），则h′(x)=bx+1−(e−x−xe−x)=bex+x2−1(x+1)e x，……其中（x+1）e x＞0，∀x∈[0，+∞），令p（x）＝be x+x2﹣1，x∈[0，+∞），则p（x）在区间[0，+∞）上单调递增，……①当b≥1时，p（x）≥p（0）＝b﹣1≥0，所以对∀x∈[0，+∞），h'（x）≥0，则h（x）在[0，+∞）上单调递增，故对任意x∈[0，+∞），h（x）≥h（0）＝0，即不等式bln（x+1）≥xe﹣x在[0，+∞）上恒成立，满足题意．…………②当0＜b＜1时，由p（0）＝b﹣1＜0，p（1）＝be＞0及p（x）在区间[0，+∞）上单调递增，所以存在唯一的x0∈（0，1）使得p（x0）＝0，且x∈（0，x0）时，p（x）＜0．即h'（x）＜0，所以h（x）在区间（0，x0）上单调递减，则x∈（0，x0）时，h（x）＜h（0）＝0，即bln（x+1）＜xe﹣x，不符合题意．……综上所述，b≥1．…………【点评】本题考查了利用利用导数研究函数的单调性极值与最值、方程与不等式的解法、分类讨论方法、等价转化方法，考查学生的运算推理能力，属于难题．。

七宝中学2019-2020学年度第二学期高二年级期中考数学试卷（时间：120分钟；满分：150分）2020.5一、填空题（1-6题每小题4分，7-12每小题5分，共54分）1.若直线,a b 均平行于平面α,那么a 与b 位置关系是__________；2.若1121101211(21)x a a x a x a x +=+++⋅⋅⋅+，则2202101311()()a a a a a a ++⋅⋅⋅+-++⋅⋅⋅+=___3.某学生在上学的路上要经过三个路口，假设在各路口是否遇到红灯是相互独立的，遇到红灯的概率都是13,则这名学生在上学的路上到第三个路口时第一次遇到红灯的概率为____4.在0120的二面角内有一点P ,P 到二面角的两个半平面的距离分别为1米和3米，则P 到该二面角棱的距离为__________5.若12232113C +3C ++3C 385n n n n n n n C ---+⋅⋅⋅+=,则n =__________6.7271除以100的余数是__________7.甲、乙、丙、丁四位同学各自在五一5天小长假里选择连续两天旅游，则至少有两位同学选择时间相同的概率为__________8.设,a b 是两条不同的直线，,αβ是两个不同的平面，则下列四个命题：①若,a b a α⊥⊥,则//b α②若//,a ααβ⊥,则//a β③若,a βαβ⊥⊥,则//a α④若,,a b a b αβ⊥⊥⊥,则αβ⊥其中正确的命题序号是__________9.若y =+则y 的取值范围是__________10.从6男2女共8名学生中选出队长1人，副队长1人，普通队员3人，组成5人服务队，要求服务队中至少有1名女生，共有__________种不同的选法。

（用数字作答）11.在5月6日返校体检中，学号为(1,2,3,4,5)i i =的五位同学的体重增加量()f i 是集合{}1,1.5,2,2.5kg,3,3.5kg kg kg kg kg 中的元素，并满足f(1)≤f(2)≤f(3)≤f(4)≤f(5),则这五同学的体重增加量所有可能的情况有__________种12.设S 为一个非空有限集合，记S 为集合S 中元素的个数，若集合S 的两个子集,A B 满足：A B k =I 并且A B S =U ,则称子集{},A B 为集合的一个“k -覆盖”（其中0k S ≤≤.若S n =,则S 的“k -覆盖”个数为__________二、选择题（每小题5分，共20分）13.在一次数学测试中，高二某班40名学生成绩的平均分为82,方差为10.2,则下列四个数中不可能是该班数学成绩的是（)A.100 B.85 C.65 D.5514.在正方体1111ABCD A B C D -中与1AD 成060角的面对角线的条数是（)A.4条 B.6条 C.8条 D.10条15.电子钟－－天显示的时间是从00:00到23:59,每一时刻都由4个数字组成，则一天中任一时刻显示的四个数字之和为22的概率为（)A.1240 B.1160 C.11440 D.118016.四棱锥P ABCD -底面为正方形，侧面PAD 为等边三角形，且侧面PAD ⊥底面ABCD ,点M 在底面正方形ABCD 内运动，且满足MP MC =,则点M 在正方形ABCD 内的轨迹一定是（)三、解答题（12分＋14分＋16分＋16分＋18分，共76分）17.若n 展开式中第二、三、四项的二项式系数成等差数列。

2019-2020学年上海市闵行区七宝中学高二下学期期中数学试卷一、单选题（本大题共4小题，共12.0分）1.若复数z=a+i1−2i(a∈R,i是虚数单位)是纯虚数，则|a+2i|等于()A. 2B. 2√2C. 4D. 82.条件p：π4<α<π2，条件q：f(x)=log tanαx在(0,+∞)是增函数，则p是q的()A. 充要条件B. 充分不必要条件C. 必要不充分条件D. 既不充分也不必要条件3.在三棱锥中，，是等腰直角三角形，，为中点.则与平面所成的角等于()A. B. C. D.4.如图，长方体ABCD−A1B1C1D1中，AD=CD=1，DD1=2，则直线DB1与直线BC1所成角的余弦值为()A. √3010B. √1010C. √7010D. 3√1010二、单空题（本大题共12小题，共36.0分）5.已知复数z1=3+4i，z2=t+i，，且z1⋅z2是实数，则实数t等于______．6.设复数z1，z2在复平面内的对应点关于虚轴对称，z1=2+i，则|z2z1|=______ ．7.设复数z1=1+i，z2=−2+xi(x∈R)，若z1⋅z2∈R，则x的值等于______．8.如果我们把高和底面半径相等的圆锥称为“标准圆锥”，那么母线长为2√2的“标准圆锥”的体积为______ ．9.若z∈C，且|z+3+4i|≤2，则|z|的取值范围为____________．10.在复数集中分解因式：a4−b4=．11.在复平面内，三点A，B，C分别对应复数z A，z B，z C，若z B−z Az C−z A =1+43i，则△ABC的三边长之比为______．12.若2cos2x=1，则x=______13.已知正三棱柱ABC−A1B1C1的底面边长与侧棱长相等．蚂蚁甲从A点沿表面经过棱BB1，CC1爬到点A1，蚂蚁乙从B点沿表面经过棱CC1爬到点A1.如图，设∠PAB=α，∠QBC=β，若两只蚂蚁各自爬过的路程最短，则α+β=______ ．14.如图，长方体ABCD−A1B1C1D1的棱AB=3，AD=AA1=2，E点在棱D1C1上，且D1E=13D1C1，则直线AE与DB1所成角的余弦值为______．15.给出下列命题：①如果，是两条直线，且//，那么平行于经过的任何平面；②如果平面不垂直于平面，那么平面内一定不存在直线垂直于平面；③若直线，是异面直线，直线，是异面直线，则直线，也是异面直线；④已知平面⊥平面，且∩=，若⊥，则⊥平面；⑤已知直线⊥平面，直线在平面内，//，则⊥．其中正确命题的序号是．16.如图，一个立方体的六个面上分别标有字母A、B、C、D、E、F，如图是此立方体的两种不同放置，则与D面相对的面上的字母是______ ．三、解答题（本大题共5小题，共60.0分）17.计算下列问题：18.如图，在三棱柱ABC−A1B1C1中，BB1⊥平面ABC，AB⊥BC，AA1=AB=BC=2．(Ⅰ)求证：BC1⊥平面A1B1C；(Ⅱ)求异面直线B1C与A1B所成角的大小；=λ(λ∈(0,1)，点N在线段A1B上，(Ⅲ)点M在线段B1C上，且B1MB1C的值(用含λ的代数式表示)．若MN//平面A1ACC1，求A1NA1B19.如图，在四棱锥P−ABCD中，底面ABCD是正方形，侧面PAD是正三角形，且平面PAD⊥平面ABCD．(1)求证：AB⊥平面PAD；(2)求直线PC与底面ABCD所成角的余弦值．20.已知多面体ABCDE中，DE⊥平面ACD，AB//DE，AC=AD=CD=DE=2，AB=1，M为CD的中点．(1)求证：AM//平面BCE；(2)求证：AM⊥平面CDE；(3)求直线BD与平面BCE所成角的正弦值．21.在区间D上，如果函数f(x)为增函数，而函数f(x)为减函数，则称函数f(x)为“弱增函数”.已x．知函数f(x)=1−1+x(1)判断函数f(x)在区间(0,1]上是否为“弱增函数”；|x1−x2|；(2)设x1，x2∈[0,+∞)，且x1≠x2，证明：|f(x2)−f(x1)|<12≤1−bx恒成立，求实数a，b的取值范围．(3)当x∈[0,1]时，不等式1−ax≤√1+x【答案与解析】1.答案：B解析：先用复数的乘除运算将z计算化简，根据纯虚数的概念求出a，再代入|a+2i|计算即可．本题考查了复数代数形式的混合运算，纯虚数的概念、复数的模．考查的均为复数中基本的运算与概念．解：z=a+i1−2i =(a+i)(1+2i)(1−2i)(1+2i)=a−2+(2a+1)i5.根据纯虚数的概念得出{2a+1≠0a−2=0∴a=2．∴|a+2i|=|2+2i|=√22+22=2√2故选B．2.答案：B解析：解：∵π4<α<π2，∴1<tanα，∴f(x)=log tanαx在(0,+∞)是增函数，∴p是q的充分条件；而f(x)=log tanαx在(0,+∞)是增函数，必有tanα>1，解得α∈(kπ+π4,kπ+π2)(k∈Z)，由q不是p的充分条件．综上可知：p是q的充分不必要条件．故选B．由π4<α<π2，可得1<tanα；而反之不成立．当a>1时，函数y=log a x在(0,+∞)是增函数．据此即可判断出答案．充分函数y=tanα、y=log a x的单调性及充分、必要条件的意义是解题的关键．3.答案：B解析：试题分析：先作PO⊥平面ABC，垂足为O，根据条件可证得点O为三角形ABC的外心，从而确定点O为AC的中点，然后证明BO是面PAC的垂线，从而得到∠BEO为BE与平面PAC所成的角，在直角三角形BOE中求解即可。

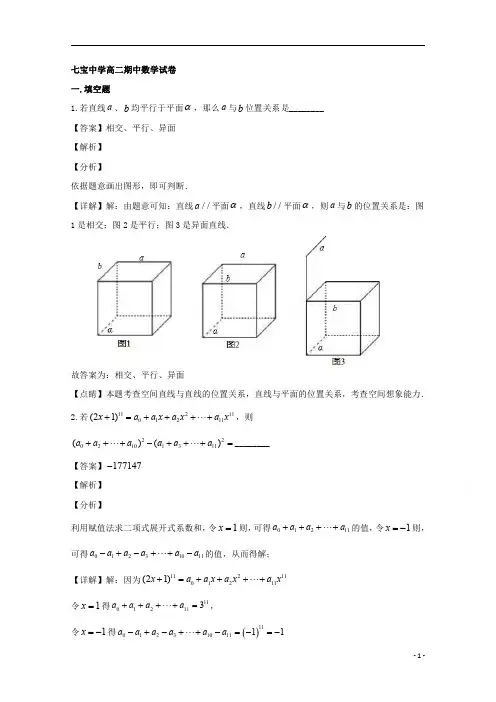
上海市七宝中学2019-2020学年高二数学9月月考试题（含解析）一.填空题1.若“0x <”是“x a <”的充分非必要条件，则实数a 的取值范围是________ 【答案】0a > 【解析】 【分析】“0x <”⇒ “x a <”,但是“x a <”⇏“0x <”，即可求解.【详解】“0x <”是“x a <”的充分非必要条件，故前者是后者的真子集，即可求得0a >。

【点睛】本题考查充分必要条件，是基础题2.函数0(2)()lg(3)1x f x x x -=-++的定义域是________【答案】(3,)+∞ 【解析】 【分析】结合对数的真数大于0，分母不为0以及0次幂底数不为0，即可求解。

【详解】解：3020310x x x x ->⎧⎪-≠⇒>⎨⎪+≠⎩，故原函数定义域为(3,)+∞.【点睛】本题考查定义域的求法，属于基础题。

3.已知向量(2,1)a =-r ，(3,4)b =r ，则向量a r 在向量b r方向上的投影为________【答案】25- 【解析】 【分析】a r 在向量b r方向上的投影为a b br r g r ，即可求解.【详解】向量a r 在向量b r方向上的投影为642cos ,55a b a b a a b a a b b-+<>====-r r r rr r r r g g g r r r g【点睛】a r 在向量b r 方向上的投影a b b r r g r ， b r 在向量a r 方向上的投影a b ar r g r ，可以直接使用，基础题。

4.已知点P是直线12PP 上一点，且1213PP PP =-uu u r uuu r ，若212P P PP λ=uuu r uuu r ，则实数λ=________【答案】23-【解析】 【分析】利用向量的三角形加法法则，即可求解。

七宝中学2019学年第二学期高二4月考试数学试卷一、填空题（本大题共有12题，满分54分）1.某公司有大量客户，且不同龄段客户对其服务的评价有较大差异．为了解客户的评价，该公司准备进行抽样调查，可供选择的抽样方法有简单随机抽样、分层抽样和系统抽样，则最合适的抽样方法是________． 【答案】分层抽样. 【解析】分析：由题可知满足分层抽样特点详解：由于从不同龄段客户中抽取，故采用分层抽样 故答案为分层抽样．点睛：本题主要考查简单随机抽样，属于基础题． 2.若事件E 与F 相互独立，且1()()4P E P F ==，则()P E F I 的值为_______（用最简分数表示）. 【答案】116【解析】 【分析】直接利用公式()=()()P E F P E P F I 计算即可.【详解】因为事件E 与F 相互独立，所以111()=()()4416P E F P E P F =⨯=I . 故答案为：116【点睛】本题考查独立事件同时发生的概率，考查学生的基本计算能力，是一道基础题.3.12x⎛+ ⎝的二项式展开式中的常数项为________（用数值作答）.【答案】495 【解析】 【分析】由二项式定理可得12x⎛+ ⎝展开式的通项为3122112rr r T C x -+=，再令31202r -=得8r =，再代入通项计算即可.【详解】由已知，12x ⎛+ ⎝展开式的通项为31212211212r r r r r r T C x C x --+==，令31202r -=， 得8r =，所以常数项为812495C =.故答案为：495【点睛】本题考查求二项展开式中的特定项，考查学生的运算能力，是一道容易题.4.计算：103237n nn n C C -+++=________（用数值作答）【答案】46 【解析】 【分析】由已知，1001023037n n n n n -≥⎧⎪-≤+⎨⎪≤≤+⎩，解不等式组可得3n =，再代入原式计算即可.【详解】由已知，1001023037n n n n n -≥⎧⎪-≤+⎨⎪≤≤+⎩，解得7732n ≤≤，又n N ∈，所以3n =，所以10379237910361046nnn n C C C C -+++=+=+=. 故答案为：46【点睛】本题考查组合数公式的计算，要注意题目中隐含的条件，考查学生的基本计算能力，是一道容易题.5.从总体中抽取6个样本：4，5，6，10，7，4，则总体方差的点估计值为________. 【答案】133【解析】 【分析】先算出6个样本数据的平均数，然后再利用方差公式计算即可. 【详解】6个样本的平均数456107466x +++++==，所以方差22222221[(46)(56)(66)(106)(76)(46)]6s =-+-+-+-+-+-261363==. 故答案为：133【点睛】本题主要考查方差的计算，考查学生的运算能力，是一道容易题.6.从正方体的6个面中取3个，其中有2个面不相邻的概率为________（用最简分数表示）. 【答案】35【解析】 【分析】利用间接法，先找到所取3个面都相邻的种数，并求出其概率，利用对立事件的概率计算公式计算即可. 【详解】从正方体的6个面中取3个共有36C 种不同结果，从8个顶点出发，3个面都相邻 共有8种不同结果，而其中有2个面不相邻的对立面是3个面都相邻， 故2个面不相邻的概率为3681231205C -==. 故答案为：35【点睛】本题考查古典概型的概率计算问题，正面情况较多可以考虑其对立事件，是一道容易题.7.直线1x y ⎧=⎪⎪⎨⎪=⎪⎩（t 为参数，t R ∈）与曲线2sin cos sin cos x y θθθθ=⎧⎨=-⎩（θ为参数，[0,2)θπ∈）的公共点的坐标为________. 【答案】()1,0 【解析】 【分析】直接利用参数方程与普通方程互化的方法分别得到直线与曲线的普通方程，解方程组即可.【详解】由15x y t⎧=+⎪⎪⎨⎪=⎪⎩消去t ，得210x y --=①，2sin cos sin cos x y θθθθ=⎧⎨=-⎩消去参数θ，得21,(11)y x x =--≤≤②，由①②解得10x y =⎧⎨=⎩或32x y =-⎧⎨=-⎩（舍），所以公共点的坐标为()1,0. 故答案为：()1,0【点睛】本题主要考查参数方程与普通方程的互化，涉及到解方程组，考查学生的计算能力，是一道容易题.8.在5(231)x y -+在展开式中，不含y 的所有项的系数和为________（用数值作答）. 【答案】243 【解析】 【分析】先将问题转化为5(21)x +各项的系数之和，再通过赋值法即可得到答案.【详解】5(231)x y -+=5(213)x y +-，其展开式的通项为515(21)(3)rrr r T C x y -+=+-，不含y 的项的系数和等于5(21)x +各项的系数之和，令1x =，得53243=. 故答案为：243【点睛】本题考查二项展开式的通项公式，考查学生的数学运算能力，本题可以直接令1,0x y ==得到答案，是一道中档题.9.从集合{}23|1,nM z z i i i i n N ==+++++∈L ________（用最简分数表示）. 【答案】13【解析】 【分析】先化简集合M ，再利用古典概型的概率计算公式计算即可.【详解】由已知，123111n ni z i i i i i+-=+++++=-L ，当4,n k k N =∈时，41411()111n n i i iz i i+--⋅===--；当41,n k k N =+∈时，424211()21111n n i i i z i i i i +--⋅====+---；当42,n k k N =+∈时，434311()1111n n i i i iz i i i i +--⋅+====---；当43,n k k N =+∈时，444111()011n n i i z i i++--===--；所以{}0,1,,1M i i =+，故从M 中任取2个元素相加有246C =种不同结果，{1,1}i +，{,1}i i +共2种不同结果，根据古典概型的概率计算公式可得所求的概率为2163=. 故答案为：13【点睛】本题考查古典概型的概率计算问题，涉及到复数的运算，考查学生的运算求解能力，是一道中档题.10.已知袋中有()*82,n n n N+≥∈个大小相同的编号球，其中黄球8个，红球n 个，从中任取两个球，取出的两球是一黄一红的概率为n P ，则n P 的最大值为________（用最简分数表示）. 【答案】815【解析】 【分析】先求出11828165615n nn C C C n n P +⋅==++，只需求出56n n+的最小值即可，结合对勾函数的性质即可得到答案. 【详解】由已知，11822816161656(8)(7)155615n n n C C n n C n n n n n nP +⋅====++++++，又易知函数56y x x =+在上单调递减，在)+∞上单调递增，因为78<<， 所以56n n +的最小值应在7n =或8n =处取得，又5656781578+=+=， 所以min 56()15n n +=，118281616856301515n n n C C C n nP +⋅==≤=++. 故答案为：815【点睛】本题考查古典概型的概率计算问题，涉及到利用对勾函数的性质求函数的最值问题，考查学生的运算求解能力，是一道中档题.11.已知关于x 的实系数方程2220x x +=-和2210x mx ++=的四个不同的根在复平面内对应的点共圆．则m 取值的集合是______. 【答案】3112m m m ⎧⎫-<<=-⎨⎬⎩⎭或【解析】【详解】易知方程2220x x -+=的两根为11x i =+，21x i =-.当2440m ∆=-<，即11m -<<时，方程2210x mx ++=有两个共轭的虚根34x x 、，且34x x 、的实部为1m -≠，此时，12x x 、对应的点在以34x x 、对应的点为直径端点的圆上，该圆的方程为()()2340x x x x y --+=，即()2234340x y x x x x x +-++=.将342x x m +=-，341x x =及12x x 、对应点的坐标()1,1±代入方程，得32m =-. 故m 的取值范围是3112m m m 或⎧⎫-<<=-⎨⎬⎩⎭.12.假设一个随机数发生器一次只能从1，2，3，…，9这九个数学中等可能地选一个数，则该随机数发生器完成了(1)n n >次选择后，选出的n 个数的乘积能被10整除的概率为________（用含n 的代数式示）.【答案】85419n n nn+-- 【解析】 【分析】由题意n 个数中，至少有一次选择了5，至少有一次选择了偶数2、4、6、8之一，设事件A 表示没有一次选择了5，事件B 表示没有一次选择了偶数，则所求概率是1()P A B -U ，再利用加法公式()()()()P A B P A P B P A B ⋃=+-⋂计算即可.【详解】为使选出的n 个数的乘积能被10整除，其中至少有一次选择了5，并且至少有一次选择了 偶数2、4、6、8之一，设事件A 表示没有一次选择了5，事件B 表示没有一次选择了偶数， 则所求概率是1()P A B -U ，从而1()1()()()P A B P A P B P A B -=--+U I8541()()()999n n n =--+=85419n n nn+--. 故答案为：85419n n nn+-- 【点睛】本题考查古典概型的概率计算以及概率的加法公式，考查学生的逻辑推理能力，是一道中档题.二、选择题（本大题共有4题，满分20分）13.若虚数1z ，2z 满足12=z z ，则“1z 与2z 互为共轭复数”是“12z z R ⋅∈”的（ ）A. 充分非必要条件B. 必要非充分条件C. 充要条件D. 即不充分也不必要条件【答案】A 【解析】 【分析】利用定义法判断即可.【详解】当1z 与2z 互为共轭复数，则12z z =，所以1221||z z z R =⋅∈， 令121,1z z ==-，满足12z z R ⋅∈，但1z 与2z 不互为共轭复数， 所以1z 与2z 互为共轭复数是12z z R ⋅∈的充分非必要条件. 故选：A【点睛】本题考查充分条件、必要条件的判断，涉及到共轭复数的相关知识，考查学生的逻辑推理能力，是一道容易题.14.某学校调查了200名学生每周的自习时间（单位：小时），制成了如图所示的频率分布直方图，其中自习时间的范围是17.5，30]，样本数据分组为17.5，20），20，22.5），22.5,25），25，27.5），27.5，30）.根据直方图，这200名学生中每周的自习时间不少于22.5小时的人数是（ ）A. 56B. 60C. 140D. 120【答案】C 【解析】【详解】试题分析：由题意得，自习时间不少于22.5小时的频率为(0.160.080.04) 2.50.7++⨯=，故自习时间不少于22.5小时的频率为0.7200140⨯=，故选C. 考点：频率分布直方图及其应用．15.某个比赛安排4名志愿者完成6项工作，每人至少完成一项，每项工作由一人完成，则不同的安排方式有多少种（ ） A. 7200种 B. 4800种 C. 2640种 D. 1560种【答案】D 【解析】 【分析】分两类，第一类，4人完成的工作数是3，1，1，1，第二类，4人完成的工作数是2，2，1，1，再将工作分组，进行分配即可. 【详解】由题意，分两类：第一类，当4人完成的工作数是3，1，1，1时，首先将6项工作分成4组，一组3项，另外三组各1项，共有3111632133C C C C A 种不同方式，再分配给4个人共311146321433480C C C C A A = 种不同方式；第二类，当4人完成的工作数是2，2，1，1时，首先将6项工作分成4组，两组2项，另外两组各1项，共有221164212222C C C C A A 种不同方式，再分配给4个人共221146421422221080C C C C A A A = 种不同方式；综上，共有1560种不同安排方式. 故选：D【点睛】本题考查排列与组合的综合应用问题，涉及到部分均匀分组问题，考查学生的逻辑推理能力，是一道中档题.16.空间内有三条直线，其中任意两条都不共面但相互垂直，直线l 与这三条直线所成角皆为θ，则tan θ=（ ）A.B.C. 1D. 直线l 不存在【答案】B 【解析】 【分析】在正方体中，设,,AB a AD b AE c ===，直线l 为AC ，由已知，BAC EAC CAD θ∠=∠=∠=，可得a b c ==，从而tan tan BC BAC AB aθ=∠==，代入a b c ==即可得到答案. 【详解】由题意，可将问题放入长方体中研究，设,,AB a AD b AE c ===，直线l 为AC ，由已知，BAC EAC CAD θ∠=∠=∠=，易得AB ⊥平面BCF ,所以222cos AB BAC AC a b c∠==++，同理可得 222cos AE EAC AC a b c ∠==++，222cos AD CAD AC a b c∠==++， 所以222a b c =++222a b c ++222a b c =++，即a b c ==，所以22tan tan 2BC c b BAC AB aθ+=∠===.故选：B【点睛】本题考查求空间中直线所成的角，考查学生的空间想象能力、数学运算能力，是一道中档题.三、解答题（本大题共有5题，满分76分）17.从A ，B ，C 等8人中选出5人排成一排. （1）A 必须在内，有多少种排法？ （2）A ，B ，C 三人不全内，有多少种排法？（3）A ，B ，C 都在内，且A ，B 必须相邻，C 与A ，B 都不相邻，都多少种排法？ （4）A 不允许站排头和排尾，B 不允许站在中间（第三位），有多少种排法？ 【答案】（1）4200种；（2）5520；（3）240；（4）4440 【解析】 【分析】（1）只需从余下的7人中选4人出来排列即可； （2）采用间接法；（3）先从余下5人中选2人有25C 种不同结果，由于A ，B 必须相邻，C 与A ，B 都不相邻，利用捆绑法、插空法即可解决；（4）分所选的5人无A 、B ，有A 、无B ，无A 、有B ，有A 、B 四种情况讨论即可.【详解】（1）由题意，先从余下的7人中选4人共有47C 种不同结果，再将这4人与A 进行全排 列有55A 种不同的排法，故由乘法原理可知共有45754200C A =种不同排法；（2）从8人中任选5人排列共有58A 种不同排法，A ，B ，C 三人全在内有2555C A 种不同排 法，由间接法可得A ，B ，C 三人不全在内共有58A -25555520C A =种不同排法； （3）因A ，B ，C 都在内，所以只需从余下5人中选2人有25C 种不同结果，A ，B 必须 相邻，有22A 种不同排法，由于C 与A ，B 都不相邻，先将选出的2人进行全排列共有22A 种不同排法，再将A 、B 这个整体与C 插入到选出的2人所产生的3各空位中有23A 种不同 排法，由乘法原理可得共有22225223240C A A A =种不同排法； （4）分四类：第一类：所选的5人无A 、B ，共有56720A =种排法；第二类：所选的5人有A 、无B ，共有4146341080C C A =种排法； 第三类：所选的5人无A 、有B ，共有4146441440C C A =种排法； 第四类：所选5人有A 、B ，若A 排中间时，有3464C A 种排法，若A 不排中间时，有31136233C C C A 种排法，共有3411364233()1200C A C C A +=种排法； 综上，共有4440种不同排法.【点睛】本题考查排列与组合的综合应用，求排列与组合的应用题的主要方法有：1.优先法，2.捆绑法，3.插空法，4.间接法，5.先整体后局部，考查学生的逻辑推理能力，是一道中档题.18.某工厂生产A ，B ，C 三种纪念品，每种纪念品均有普通型和精品型两种，某一天产量如下表（单位：个）：现采用分层抽样的方法在这一天生产的纪念品中抽取100个，其中有A 种纪念品40个.（1）若再用分层抽样的方法在所有B 种纪念品中抽取一个容量为13的样本.将该样本看成一个总体，从中任取2个纪念品，求至少有1个精品型纪念品的概率（用最简分数表示）；（2）从C 种精品型纪念品中抽取6个，其某种指标的数据分别如下：4，7，x ，y ，8，5.把这6个数据看作一个总体，其均值为7、方差为6，求x y -的值. 【答案】（1）1126；（2）【解析】 【分析】（1）先由抽样比算出n ，进一步得到13个样本中精品型的个数，再利用古典概型的概率计算公式计算即可；（2）利用平均数、方差可得18x y +=，22176x y +=，进一步得到2148xy =，代入x y -.【详解】（1）由已知，10040(800200)800200150500350n =+⨯+++++，解得500n =，B 种纪念品中抽取一个容量为13的样本中，精品型有131503150500⨯=+个， 从13个纪念品中任取2个有213C 中不同结果，无精品型有210C 种不同结果，所以至少有1个精品型纪念品的概率为210213151126C C -=-=1126. （2）由题意，1(4785)76x y +++++=，所以18x y +=， 又2222221[(47)(77)(7)(7)(87)(57)]66x y -+-+-+-+-+-=， 所以22(7)(7)22x y -+-=，即2214()9822176x y x y +=+-+=， 所以2222()()148xy x y x y =+-+=，故x y -=.【点睛】本题考查统计与概率的简单应用，涉及到分层抽样、平均数、方差的计算，考查学生的运算能力，是一道容易题.19.如图所示，某街道居委会拟在EF 地段的居民楼正南方向的空白地段AE 上建一个活动中心，其中30AE =米．活动中心东西走向，与居民楼平行. 从东向西看活动中心的截面图的下部分是长方形ABCD ，上部分是以DC 为直径的半圆. 为了保证居民楼住户的采光要求，活动中心在与半圆相切的太阳光线照射下落在居民楼上的影长GE 不超过2.5米，其中该太阳光线与水平线的夹角θ满足3tan 4θ=.（1）若设计18AB =米，6AD =米，问能否保证上述采光要求？（2）在保证上述采光要求的前提下，如何设计AB 与AD 的长度，可使得活动中心的截面面积最大？（注：计算中π取3）【答案】（Ⅰ）能（Ⅱ）20AB =米且5AD =米 【解析】 【分析】 （1）以点A坐标原点，AB 所在直线为x 轴，建立平面直角坐标系．设太阳光线所在直线方程为y=34x+b ，利用直线与圆相切，求出直线方程，令x=30，得EG=1.5米＜2.5米，即可得出结论；（2）欲使活动中心内部空间尽可能大，则影长EG 恰为2.5米，即可求出截面面积最大. 【详解】解：如图，以A 为坐标原点，AB 所在直线为x 轴，建立平面直角坐标系．（1）因为AB ＝18米，AD ＝6米， 所以半圆的圆心为H (9,6)，半径r ＝9. 设太阳光线所在直线方程为y ＝－34x ＋b ， 即3x ＋4y －4b ＝02227+24-4b 3+4＝9，解得b ＝24或b ＝32(舍)． 故太阳光线所在直线方程为y ＝－34x ＋24, 令x ＝30，得EG ＝1.5＜2.5. 所以此时能保证上述采光要求． （2）设AD ＝h 米，AB ＝2r 米，则半圆的圆心为H(r，h)，半径为r.方法一设太阳光线所在直线方程为y＝－34x＋b，即3x＋4y－4b＝0，r，解得b＝h＋2r或b＝h－r2(舍)．故太阳光线所在直线方程为y＝－34x＋h＋2r，令x＝30，得EG＝2r＋h－452，由EG≤52，得h≤25－2r.所以S＝2rh＋12πr2＝2rh＋32×r2≤2r(25－2r)＋32×r2＝－52r2＋50r＝－52(r－10)2＋250≤250.当且仅当r＝10时取等号．所以当AB＝20米且AD＝5米时，可使得活动中心的截面面积最大．方法二欲使活动中心内部空间尽可能大，则影长EG恰为2.5米，则此时点G为(30,2.5)，设过点G的上述太阳光线为l1，则l1所在直线方程为y－52＝－34(x－30)，即3x＋4y－100＝0.由直线l1与半圆H相切，得r＝3r+4h-1005.而点H(r，h)在直线l1的下方，则3r＋4h－100＜0，即r＝－3r+4h-1005，从而h＝25－2r.又S＝2rh＋12πr2＝2r(25－2r)＋32×r2＝－52r2＋50r＝－52(r－10)2＋250≤250.当且仅当r＝10时取等号．所以当AB＝20米且AD＝5米时，可使得活动中心的截面面积最大．【点睛】本题考查利用数学知识直线与圆的相切位置关系解决实际问题，考查二次函数配方法的运用和分析解决实际问题的能力，属于中档题．20.已知数列{}n a 的首项为1.记()12*12()knn n k n n n f n a C a C a C a C n N=++⋅⋅⋅+⋅⋅+∈+⋅.（1）若{}n a 为常数列，求(3)f 的值：（2）若{}n a 为公比为2的等比数列，求()f n 的解析式：（3）是否存在等差数列{}n a ，使得()1(1)2n f n n -=-对一切*n N ∈都成立？若存在，求出数列{}n a 的通项公式：若不存在，请说明理由.【答案】（1）(3)7f =（2）31()2n f n -=（3）存在等差数列{}n a 满足题意，21n a n =-【解析】 【分析】(1)根据常数列代入其值得解；(2)根据等比数列和用赋值法解决二项式展开式的相关问题求解；(3)对于开放性的问题先假设存在等差数列，再推出是否有恒成立的结论存在，从而得结论. 【详解】解：（1）∵{}n a 为常数列，∴()1n a n N +=∈.∴123333(3)7f C C C =++=（2）∵{}n a 为公比为2的等比数列，()12n n a n N -+=∈.∴1231()242n nn n n n f n C C C C -=+++L∴1223312()12222n nn n n n f n C C C C +=++++L(12)3n n +=故31()2n f n -=. （3）假设存在等差数列{}n a ，使得()1(1)2nf n n -=-对一切*n N ∈都成立，设公差为d ，则()12*12()k nn n k n n n f n a C a C a C a C n N=+++++∈L L1111()n n k n n n n k n n f n a C a C a C a C --=+++++L L相加得()()121112()2k n n n n n n n f n a a a C C C C --=++++++L L∴()11()222nn n a a f n a -+=+-()11(1)[2(2)]21n n d n d -=+-++--. ∴1()1(2)[2(2)]2(1)2n n f n d n d n --=-++-=-恒成立， 即1(2)(2)(2)20n d d n --+--=n ∈+N 恒成立，∴2d =故{}n a 能为等差数列，使得()1(1)2n f n n -=-对一切n ∈+N 都成立，它的通项公式为21n a n =- 【点睛】本题关键在于观察所求式子的特征运用二项式展开式中的赋值法的思想，属于难度题.21.已知点1F 、2F 为双曲线222:1y C x b-=(0)b >的左、右焦点，过2F 作垂直于x 轴的直线，在x 轴上方交双曲线C 于点M ，且1230MF F ∠=︒，圆O 的方程是222x y b +=. （1）求双曲线C 的方程；（2）过双曲线C 上任意一点P 作该双曲线两条渐近线的垂线，垂足分别为1P 、2P ，求12PP PP ⋅u u u v u u u v的值； （3）过圆O 上任意一点Q 作圆O 的切线l 交双曲线C 于A 、B 两点，AB 中点为M ，求证：||2||AB OM = 【答案】（1）2212y x -=；（2）1229PP PP ⋅=u u u r u u u r ；（3）详见解析. 【解析】 【分析】（1）222b MF b a==，根据1230MF F ∠=o可得21||2MF b =，利用双曲线的定义可得22b =从而得到双曲线的方程.（2）设点()00,P x y ，利用渐近线的斜率可以得到12,PP PP u u u v u u u v 夹角的余弦为13，利用点在双曲线上又可得12PP PP ⨯u u u v u u u v 为定值23，故可得12·PP PP u u u vu u u v 的值. （3）设1122(,),(,)A x y B x y ，切线l 的方程为:002x x y y +=，证明2AB OM =等价于证明OA OB ⊥，也就是证明 12120x x y y +=，联立切线方程和双曲线方程，消元后利用韦达定理可以证明12120x x y y +=.【详解】(1)设2,F M 的坐标分别为,0)y因为点M 在双曲线C 上,所以22021+1y b b-=,即20y b =±,所以22||MF b =，在21Rt MF F ∆中, 1230MF F ∠=o,22||MF b =,所以21||2MF b =， 由双曲线的定义可知: 212||||2MF MF b -==，故双曲线C 的方程为: 2212y x -=.(2)由条件可知:两条渐近线分别为10l y -=；20l y +=. 设双曲线C 上的点00(,)Q x y , 设1l 的倾斜角为θ，则tan θ=0,2πθ⎛⎫∈ ⎪⎝⎭，所以cos θ=， 故21cos 22cos 13θθ=-=-， 所以12,PP PP u u u v u u u v的夹角为2πθ-，且()1cos 23πθ-=. 点Q到两条渐近线的距离分别为1||PP =，2||PP =.因为00(,)Q x y 在双曲线22:12y C x -=上,所以220022x y -= ，所以12PP PP ⋅=u u u r u u ur ()2200212cos 2339x y πθ--=⋅=. (3)由题意,即证: OA OB ⊥,设1122(,),(,)A x y B x y , 切线l 的方程为: 002x x y y +=.00y ≠时,切线l 的方程代入双曲线C 中,化简得:(222000(2)4y x x x x -+20(24)0y -+=，所以01222004(2)x x x y x +=--，20122200(24)(2)y x x y x +=--. 又01021200(2)(2)x x x x y y y y --=⋅012201[42()x x x y =-+220012220082]2x x x x y x -+=-， 所以1212OA OB x x y y ⋅=+u u u r u u u r 220022220000(24)82(2)2y x y x y x +-=-+--2200220042()02x y y x -+==-. 00y =时,易知上述结论也成立.所以12120OA OB x x y y ⋅=+=u u u r u u u r.综上, OA OB ⊥,所以||2||AB OM =u u u r u u u u r.【点睛】（1）过焦点且垂直于实轴的直线与双曲线()222210.0x y a b a b -=>> 交于,A B ，则22b AB a=（通径）.（2）直线与圆锥曲线的位置关系，一般可通过联立方程组并消元得到关于x 或y 的一元二次方程，再把要求解的目标代数式化为关于两个的交点横坐标或纵坐标的关系式，该关系式中含有1212,x x x x +或1212,y y y y +，最后利用韦达定理证明该关系式为恒等式.。

2019-2020年高二下学期期中考试数学理试题一、选择题（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．每小题选出答案后。

）1. 复数1011⎪⎭⎫⎝⎛+-i i 的值是（ ） A ．－1 B ．1 C ．32 D ．－322. 若C z ∈且|22|,1||i z z --=则的最小值是（ ）A ．22B ．212-C ．22+1D ．2-1 3. 如图所示，正方形的四个顶点分别为(0,0),(1,0),(1,1),(0,1)O A B C ，曲线2yx =经过点B ，现将一个质点随机投入正方形中，则质点落在图中阴影区域的概率是（ ） A ．12 B ．14 C ．13 D ．254. 有四位司机、四个售票员组成四个小组，每组有一位司机和一位售票员，则不同的分组方案共有（ ）A.88A 种 B.48A 种 C.44A ·44A 种 D.44A 种5.（1）已知332p q +=，求证2p q +≤，用反证法证明时，可假设2p q +≥； （2）已知a b ∈R ，，1a b +<，求证方程20x ax b ++=的两根的绝对值都小于1．用反证法证明时可假设方程有一根1x 的绝对值大于或等于1，即假设11x ≥，以下结论正确的是（ ）Ａ．(1)与(2)的假设都错误 Ｂ．(1)与(2)的假设都正确Ｃ．(1)的假设正确；(2)的假设错误 Ｄ．(1)的假设错误；(2)的假设正确6.用数学归纳法证明“)12(212)()2)(1(-⋅⋅⋅⋅=+++n n n n n n”（+∈N n ）时，从“1+==k n k n 到”时，左边应增添的式子是（ ）A.12+kB.)12(2+kC.112++k kD.122++k k 7. 经过抛物线212x y =的焦点,且斜率为1-的直线方程为( ) A. 161610x y +-= B. 2210x y +-= C. 4410x y +-= D. 8810x y +-=8.若一个椭圆长轴的长度、短轴的长度和焦距成等差数列，则该椭圆的离心率是( ) A. 51 B. 52 C. 53 D. 549．下面几种推理过程是演绎推理的是( )A ．两条直线平行，同旁内角互补，如果A ∠和B ∠是两条平行直线的同旁内角，则180A B ∠+∠=︒．B ．由平面三角形的性质，推测空间四面体性质．C ．某校高二共10个班，1班51人，2班53人，3班52人，由此推测各班都超过50人D ．在数列{}n a 中()111111,22n n n aa a n a --⎛⎫==+≥ ⎪⎝⎭，由此归纳出{}n a 的通项公式． 10．如图，直线从o l 开始在平面上绕点O 按逆时针方向匀速 （转动角度不超过90度）时，它扫过的园内阴影部分的面积S 是时间t 的函数，这个函数的图像大致是（ ）11.设a R ∈，若函数x ye ax =+，x R ∈，有大于零的极值点，则（ ）A ．1a <-B 。

2019上海市高二第二学期期中数学试题一、单选题1．《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题:“今有委米依垣内角，下周八尺，高五尺.问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图，米堆为一个圆锥的四分之一)，米堆为一个圆锥的四分之一)，米堆底部的弧长为8尺，米堆的高为5尺，问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺，圆周率约为3，估算出堆放的米约有A．14斛B．22斛C．36斛D．66斛【答案】B【解析】试题分析：设圆锥底面半径为r，则，所以，所以米堆的体积为=，故堆放的米约为÷1.62≈22，故选B.【考点】圆锥的性质与圆锥的体积公式2．“两条直线没有公共点”是“两条直线为异面直线”的（）A.充分非必要条件B.必要非充分条件C.充要条件D.既非充分又非必要条件【答案】B【解析】两直线没有公共点则平行或异面；根据异面直线定义可知异面直线无公共点，从而得到结果.【详解】两条直线没有公共点，则两条直线平行或异面，充分条件不成立；若两条直线为异面直线，则两条直线不共面，则必然没有公共点，必要条件成立“两条直线没有公共点”是“两条直线为异面直线”的必要非充分条件故选：B【点睛】本题考查充分条件、必要条件的判定，涉及到异面直线定义的应用，属于基础题. 3．集合{M =正四棱柱}，{P =直四棱柱}，{N =长方体}，{Q =正方体}，则这四个集合之间的关系是（ ） A.P n N n M n Q B.P n M n N n Q C.Q n M n N n P D.Q n N n M n P【答案】C【解析】根据直四棱柱、长方体、正四棱柱和正方体的定义可得到结果. 【详解】直四棱柱是底面为四边形，侧棱和底面垂直的四棱柱； 长方体是底面为矩形的直四棱柱； 正四棱柱是底面为正方形的直四棱柱； 正方体是侧棱长和底面边长相等的正四棱柱；∴Q n M n N n P故选：C 【点睛】本题考查空间几何体的结构特征，需熟练掌握直四棱柱、长方体、正四棱柱和正方体的结构特征，属于基础题.4．一个正方体被一个平面截去一部分后，剩余部分的三视图如图，则截去部分体积与剩余部分体积的比值（ ）正视图 侧视图 俯视图 A.15B.16C.12D.18【答案】A【解析】由三视图可确定截面为平面11AB D ，可知截掉部分为三棱锥111A AB D -，由三棱锥体积公式求得111A A B D V -，即为截去部分体积，从而得到剩余部分体积为3316a a -，作比得到结果. 【详解】由三视图可知，剩余部分为正方体1111ABCD A B C D -沿平面11AB D 截掉三棱锥111A AB D -后得到的图形设正方体棱长为a 11113ABCD A B C D V a -∴=，111111111311136A AB D A A B D A B D V V S AA a --∆==⋅=∴截去部分体积与剩余部分体积之比为：333111:665a a a ⎛⎫-= ⎪⎝⎭故选：A 【点睛】本题考查正方体截面的问题，关键是能够通过三视图确定截面，从而得到确定截掉的部分的体积.5．如图，四个棱长为1的正方体排成一个正四棱柱，AB 是一条侧棱，()1,2,,8i P i =L 是上底面上其余的八个点，则()1,2,,8i AB AP i ⋅=⋅⋅⋅u u u r u u u r的不同值的个数为（ ）A.8B.4C.2D.1【答案】D【解析】根据平面向量运算法则可知2i i AB AP AB AB BP ⋅=+⋅u u u r u u u r u u u r u u u r u u u r ，由线面垂直性质可知0i AB BP ⋅=u u u r u u u r，从而得到21i AB AP AB ⋅==u u u r u u u r u u u r ，进而得到结果. 【详解】()2i i i AB AP AB AB BP AB AB BP ⋅=⋅+=+⋅u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u rAB ⊥Q 平面286BP P P i AB BP ∴⊥u u u r u u u r 0i AB BP ∴⋅=u u u r u u u r21i AB AP AB ∴⋅==u u u r u u u r u u u r则()1,2,,8i AB AP i ⋅=⋅⋅⋅u u u r u u u r 的不同值的个数为1个故选：D 【点睛】本题考查向量数量积的求解问题，关键是能够利用平面向量线性运算将所求向量数量积转化为已知模长的向量和有垂直关系向量的数量积的运算问题，考查了转化与化归的思想.二、填空题6．空间不共面的四个点可以确定__________个平面. 【答案】4【解析】由三点确定一个平面可知共有4种情况，由此得到结果. 【详解】不共面的四个点中任意三个点可构成一个平面，则共可确定4个平面 故答案为：4 【点睛】本题考查空间中平面的确定，属于基础题.7．已知正方体1111ABCD A B C D -的棱长为a ，异面直线BD 与11A B 的距离为__________. 【答案】a【解析】根据线面垂直性质可得1BB BD ⊥，又111BB A B ⊥，可知所求距离为1BB ，从而得到结果. 【详解】1BB ⊥Q 平面ABCD ，BD ⊂平面ABCD 1BB BD ∴⊥又111BB A B ⊥ ∴异面直线BD 与11A B 之间距离为1BB a = 故答案为：a 【点睛】本题考查异面直线间距离的求解，属于基础题.8．在正方体1111ABCD A B C D -中，二面角1C AB D --的大小为__________. 【答案】4π 【解析】由线面垂直性质得1BC AB ⊥，又BC AB ⊥，可得二面角平面角为1C BC ∠，由14C BC π∠=得到结果.【详解】AB ⊥Q 平面11BCC B ，1BC ⊂平面11BCC B 1BC AB ∴⊥又BC AB ⊥，BC ⊂平面ABD 1C BC ∴∠即为二面角1C AB D --的平面角14C BC π∠=Q ∴二面角1C AB D --的大小为4π 故答案为：4π 【点睛】本题考查立体几何中二面角的求解，关键是能够根据二面角平面角的定义找到二面角的平面角.9．如图，在棱长为3cm 的正四面体A BCD -中，若以ABC ∆为视角正面，则其主视图的面积是__________2cm .【答案】36 2【解析】确定正视图为三角形，且底边长为底面三角形边长，高为四面体的高；求得正四面体的高后，即可求得结果.【详解】由题意可得，正视图是以底面三角形边长为底边长，正四面体A BCD-的高为高的三角形Q正四面体棱长为3∴933 942 -=∴正四面体的高22339632AO⎛⎫=-⨯=⎪⎪⎝⎭∴正视图的面积为：1363622⨯=36【点睛】本题考查几何体三视图的求解问题，关键是能够根据给定视角确定正视图的图形构成，属于基础题.10．若正六棱柱的所有棱长均为m，且其体积为123m=__________.【答案】2【解析】根据底面为边长为m的正六边形可求得底面面积，进而利用棱柱体积公式构造方程求得结果.【详解】Q正六棱柱底面为边长为m的正六边形∴底面面积为：()2222m m +⨯=∴正六棱柱体积2V m =⋅=2m =故答案为：2 【点睛】本题考查棱柱体积的相关计算，关键是能够熟悉正棱柱的定义，并准确求解出底面面积. 11．给出以下结论：①空间任意两个共起点的向量是共面的；②两个相等向量就是相等长度的两条有向线段表示的向量；③空间向量的加法满足结合律：()()a b c a b c ++=++r r r r rr ；④首尾相接的若干向量之和，等于由起始向量的起点指向末尾向量的终点的向量. 请将正确的说法题号填在横线上：__________. 【答案】①③④【解析】根据起点和终点3点共面，可知①正确；由相等向量定义可知②错误；根据向量加法运算律和线性运算法则可知③④正确. 【详解】①中，两个向量共起点，与两向量终点共有3个点，则3点共面，可知两向量共面，①正确；②中，两个相等向量需大小相等，方向相同，②错误； ③中，空间向量加法满足结合律，③正确； ④中，由向量加法的三角形法则可知④正确. 故答案为：①③④ 【点睛】本题考查向量部分相关命题的判定，涉及到相等向量的概念、向量加法的运算律和三角形法则的运用等知识，属于基础题.12．已知球的半径为5cm ，有两个平行平面截球所的截面面积分别等于29cm π与216cm π，则这两个平行平面的距离为__________cm .【答案】1或7【解析】利用截面面积求得截面圆半径，利用勾股定理可求得球心到两截面的距离；由两截面与球心的相对位置可确定两平行平面间距离.【详解】由截面面积可知截面圆半径分别为：3cm 和4cm∴球心到两截面的距离分别为：12594d =-=，225163d =-=∴当两截面在球心同侧时，两平行平面间距离为：431-=当两截面在球心两侧时，两平行平面间距离为：437+= 故答案为：1或7 【点睛】本题考查球的平行截面间距离的问题，易错点是忽略两平行平面可位于球心的同侧或两侧，求解时丢失其中一种情况.13．如图，在空间直角坐标系O xyz -中，四面体C OAB -的主视图AOC 是面积为43的直角三角形，且23CO =，OAB ∆是正三角形，且点B 在平面xOy 上，则此四面体的左视图的面积等于__________.【答案】6【解析】作//BD AO ，根据AO ⊥平面yOz 可知BD ⊥平面yOz ，得到左视图为COD ∆；根据AOC S ∆可求得底面正三角形边长，进而求得OD ，从而得到左视图面积.【详解】作//BD AO ，交y 轴于D ，连接CDAO ⊥Q 平面yOz ，//BD AO BD ∴⊥平面yOz∴此四面体的左视图为COD ∆12AOC S AO CO ∆=⋅==Q 4AO ∴= 122BD AO ∴==OD ∴=== 11622COD S CO OD ∆∴=⋅=⨯=故答案为：6 【点睛】本题考查空间几何体的三视图问题的求解，关键是能够根据垂直关系确定左视图的图形，从而利用长度关系来进行求解.14．已知()cos ,1,sin a θθ=r ，()sin ,1,cos b θθ=r ，则向量a b +rr 与a b -r r 的夹角是__________. 【答案】2π 【解析】利用向量坐标运算表示出a b +rr 与a b -r r ，根据数量积运算法则可求得()()0a b a b +⋅-=r rr r ，即两向量垂直，得到夹角.【详解】()sin cos ,2,sin cos a b θθθθ+=++r r ，()cos sin ,0,sin cos a b θθθθ-=--rr()()2222cos sin sin cos 0a b a b θθθθ∴+⋅-=-+-=r rr r()()a b a b ∴+⊥-r r r r ，即a b +r r 与a b -r r 的夹角为2π故答案为：2π 【点睛】本题考查向量夹角的求解，关键是能够通过向量的坐标运算求得两向量的数量积，属于基础题.15．若圆锥的侧面积与过轴的截面面积之比为2π，则其母线与轴的夹角的大小为 ． 【答案】3π 【解析】由题意得：1:(2)222rl h r l h ππ⋅=⇒=⇒母线与轴的夹角为3π 【考点】圆锥轴截面【名师点睛】掌握对应几何体的侧面积，轴截面面积计算方法.如 圆柱的侧面积，圆柱的表面积，圆锥的侧面积，圆锥的表面积，球体的表面积，圆锥轴截面为等腰三角形.16．已知函数22,01(){23,13x x f x x x x ≤≤=-++<≤，将f （x ）的图像与x 轴围成的封闭图形绕x 轴旋转一周，则所得旋转体的体积为________． 【答案】203π【解析】试题分析：将的图像与轴围成的封闭图形绕轴旋转一周，所得旋转体为一个圆锥和一个半个球的组合体，其中球的半径为2，棱锥的底面半径为2，高为1，所以所得旋转体的体积为23114202123233πππ=⨯⨯⨯+⨯⨯⨯=. 【考点】旋转体体积17．鲁班锁是中国传统的智力玩具，起源于中国古代建筑中首创的榫卵结构，它的外观是如图所示的十字立方体，其上下、左右、前后完全对称，六根等长的正四棱柱分成三组，经90︒榫卯起来.若正四棱柱的高为5，底面正方形的边长为1，现将该鲁班锁放进一个球形容器内，则该球形容器的表面积的最小值为__________.（容器壁的厚度忽略不计，结果保留π）【答案】30π【解析】由榫卯结构可确定球形容器半径的最小值，进而利用球的表面积公式求得结果. 【详解】22213052122++=∴该球形容器表面积的最小值为：230430ππ⨯=⎝⎭故答案为：30π本题考查球的表面积的求解问题，关键是能够根据位置关系确定球的半径的最小值，进而应用球的表面积公式求得结果.三、解答题18．已知向量b r 与向量()2,1,2a =-r 共线，且18a b ⋅=r r ，()()ka b ka b +⊥-r r r r ，求实数k 的值.【答案】2k =±【解析】根据向量共线可设b a λ=r r ，由18a b ⋅=r r 可构造方程求得λ，得到b r；由向量垂直可得()()0ka b ka b +⋅-=r r r r ，由数量积运算律可构造方程求得k . 【详解】,a b r r Q 共线 ∴可设()2,,2b a λλλλ==-r r44918a b λλλλ∴⋅=++==r r ，解得：2λ= ()4,2,4b ∴=-r()()ka b ka b +⊥-r r r r Q ()()2220ka b ka b k a b ∴+⋅-=-=r r r r r r 即()()2414164160k ++-++=，解得：2k =± 【点睛】本题考查根据向量的平行、垂直关系求解参数值的问题，关键是能够明确向量共线的条件、向量垂直的坐标表示，属于基础题.19．已知地球的半径为R ，在北纬30°圈上有A 、B 两点.若点A 的经度为东经65︒，点B 的经度为西经25︒，求A 、B 两点的球面距离.【答案】1arccos 4R ⋅ 【解析】根据纬度的定义可知30OBO '∠=o ，从而得到纬线圈所在圆的半径，根据经度差可知90AO B '∠=o ，由勾股定理求得AB ；在AOB ∆中，由余弦定理求得cos AOB ∠，从而得到AOB ∠，由扇形弧长公式可求得球面距离.设北纬30o 的纬线圈的圆心为O '由题意可知：90AO B '∠=o ，30OBO '∠=o 122R OO OB '∴==，33O B OB R '== 3O A O B R ''∴== 226AB O A O B R ''∴=+= 在AOB ∆中，由余弦定理得：2222312cos 24R R R AOB R +-∠== 1arccos 4AOB ∴∠= ,A B ∴两点的球面距离为：1arccos 4R ⋅ 【点睛】本题考查球面距离的求解问题，关键是能够熟练掌握经度和纬度的定义，从而得到图形中的角度关系.20．底面边长为2的正三棱锥P ABC -，其表面展开图是正三角形123PP P ，如图所示.求：（1）123PP P ∆的各边长；（2）三棱锥P ABC -的体积.【答案】（1）各边均为4；（2）23【解析】（1）由123PP P ∆为正三角形，可知三边长均为2AB ，根据2AB =可得结果； （2）根据正三棱锥的特点可求得三棱锥的高，求得底面面积后，根据三棱锥体积公式可求得结果.（1）123PP P ∆Q 为正三角形12231324PP P P PP AB ∴====（2）23234ABC S ∆=⨯=立体图形中求三棱锥的高：()22323633h ⎛⎫=-= ⎪ ⎪⎝⎭ 11222363333P ABC ABC V S h -∆∴=⨯⨯=⨯⨯= 【点睛】本题考查正三棱锥的结构特征、三棱锥体积的求解问题，属于基础题.21．在长方体1111ABCD A B C D -中，2AB BC ==，过1A 、1C 、B 三点的平面截去长方体的一个角后，得到如图所示的几何体111ABCD AC D -，且这个几何体的体积为10.（1）求直线1A B 与平面1ADD 所成的角的大小；（2）求点1D 到平面11A BC 的距离.【答案】（1）2arctan 3；（2）32211【解析】设长方体高为h ，由长方体体积减去截掉的三棱锥体积可得几何体111ABCD AC D -体积，由此建立方程求得3h =；（1）根据直线与平面所成角定义可知1BA A ∠即为所求角，由112tan 3AB BA A AA ∠==可（2）设所求距离为d ，由等体积法可知111111D A BC B A D C V V --=，由此构造关于d 的方程，解方程求得结果.【详解】设长方体的高1AA h =则几何体111ABCD AC D -体积：142103V h h =-⨯⨯=，解得：3h =（1）AB ⊥Q 平面11ADD A ∴直线1A B 与平面1ADD 所成角即为1BA A ∠ 112tan 3AB BA A AA ∠==Q ∴所求线面夹角为：2arctan 3（2）设点1D 到平面11A BC 的距离为d则由111111D A BC B A D C V V --=得：1111111133A BC A D C S d S BB ∆∆⋅⋅=⋅⋅ 11A BC ∆Q 为等腰三角形，114913A B BC ==+=，114422AC =+=∴13211-= 1112211222A BC S ∆∴=⨯=又11112222A D C S ∆=⨯⨯= 11222333d ∴=⨯⨯，解得：322d =即点1D 到面11A BC 的距离为32211 【点睛】本题考查立体几何中直线与平面所成角、点到面的距离的求解问题；立体几何中求解点到面的距离常采用等体积法，将问题转化为三棱锥高的求解，从而利用等体积转化构造方程求得结果，属于常考题型.22．已知圆锥的顶点为P ，底面圆心为O ，母线长为4，23PO =OA 、OB 是底面半径，且：0OA OB ⋅=u u u r u u u r，M 为线段AB 的中点，N 为线段PB 的中点，如图所示：（1）求圆锥的表面积；（2）求异面直线PM 和OB 所成的角的大小，并求A 、N 两点在圆锥侧面上的最短距离.【答案】（1）12π；（2）PM 、OB 夹角为arctan 13，最短距离为2522-【解析】（1）由22r l PO =-求得底面圆半径，根据圆锥表面积公式可求得结果； （2）作//MH BO ，根据异面直线所成角定义可知所成角为PMH ∠；根据向量数量积为零可知OA OB ⊥，进而得到MH AO ⊥，根据线面垂直性质知MH PO ⊥，得到线面垂直关系MH ⊥平面AOP ，由线面垂直性质得MH PH ⊥，根据长度关系可求得tan PMH ∠，进而求得异面直线所成角；求得圆锥侧面展开图圆心角后，根据弧长关系可求得APB ∠，由余弦定理可求得结果.【详解】（1）由题意得：底面圆半径()22224232r l PO =-=-=∴圆锥表面积28412S rl r πππππ=+=+=（2）作//MH BO ，交OA 于H ，连接PH∴异面直线PM 与OB 所成角即为PM 与MH 所成角，即PMH ∠0OA OB ⋅=u u u r u u u r Q OA OB ∴⊥，又//MH BO MH AO ∴⊥PO ⊥Q 平面OAB ，MH ⊂平面OAB MH PO ∴⊥,AO PO ⊂Q 平面AOP ，AO PO O ⊥= MH ∴⊥平面AOP又PH ⊂平面AOP MH PH ∴⊥M Q 为AB 中点，//MH BO H ∴为AO 中点 112MH OB ∴==，221121132PH PO OA ⎛⎫=+=+= ⎪⎝⎭tan 13PH PMH MH∴∠== arctan 13PMH ∴∠= 即异面直线PM 与OB 所成角大小为arctan 13由44πα=得：απ=，即圆锥侧面展开图扇形圆心角为π圆锥侧面展开图如下图所示：124AB r ππ=⋅=Q 4APB BP ππ∴∠== N Q 为BP 中点 2PN ∴=在APN ∆中，由余弦定理可得：2222cos 2082AN AP PN AP PN APN =+-⋅∠=-2522AN ∴=-,A N 两点在圆锥侧面上的最短距离为2522-【点睛】本题考查圆锥表面积的求解、异面直线所成角的求解、利用侧面展开图求解两点间的最短距离问题；求解最短距离的方法为利用侧面展开图，通过两点之间线段最短，从而确定所求的线段，利用余弦定理求得结果.。

2019-2020学年上海市闵行区七宝中学高二（下）期末数学试卷试题数：21.满分：01.（填空题.3分）已知集合A={（x.y ）|x 2+y 2=1}.B={（x.y ）|y=-x}.则A∩B 中元素的个数是___ ．2.（填空题.3分）若平面α外的直线a 与平面α所成角为θ.则θ的取值范围是___ ．3.（填空题.3分）已知 AM ⃗⃗⃗⃗⃗⃗ =（0.1.2）. CN ⃗⃗⃗⃗⃗ =（1.0.2）.则直线AM 和CN 所成角的余弦值是___ ．4.（填空题.3分）在北纬45°圈上有A 、B 两点.若该纬度圈上A 、B 两点间的劣弧长为 √24 πR （R 为地球的半径）.则A 、B 两点间的球面距离是___ ．5.（填空题.3分）设x 、y 满足约束条件 {x +2y −2≥0x −y +1≥02x −y −4≤0 .则z=2x+y 的最大值是___ ．6.（填空题.3分）不等式mx 2-mx-2＜0对任意x∈R 恒成立的充要条件是m∈___ ．7.（填空题.3分）某圆柱的高为2.底面周长为16.其三视图如图.圆柱表面上的点M 在正（主）视图上的对应点为A.圆柱表面上的点N 在侧（左）视图上的对应点为B.则在此圆柱侧面上.从M 到N 的路径中.最短路径的长度为 ___ ．8.（填空题.3分）有一多边形ABCD 水平放置的斜二测直观图A′B′C′D′是直角梯形（如图所示）.其中∠A'B′C′=45°.B′C′⊥C′D′.A′D′=D′C′=1.则原四边形ABCD 的面积为___ ．9.（填空题.3分）正四棱柱ABCD-A 1B 1C 1D 1中.AB=AD=1.E 为BB 1中点.若点P 满足 AP ⃗⃗⃗⃗⃗ = λPD ⃗⃗⃗⃗⃗ .且BP || 平面AED 1.则λ=___ ．10.（填空题.3分）在正方体ABCD-A 1B 1C 1D 1中.给出下面四个命题： ① （ A 1A ⃗⃗⃗⃗⃗⃗⃗ + A 1D 1⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ +A 1B 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ ）2=3（ A 1A ⃗⃗⃗⃗⃗⃗⃗ ）2； ② AD 1⃗⃗⃗⃗⃗⃗⃗ 与 A 1B ⃗⃗⃗⃗⃗⃗⃗ 夹角为120°； ③ A 1C ⃗⃗⃗⃗⃗⃗⃗ •C 1D ⃗⃗⃗⃗⃗⃗⃗ =0； ④ 正方体的体积是| AB ⃗⃗⃗⃗⃗ • BC ⃗⃗⃗⃗⃗ • CC 1⃗⃗⃗⃗⃗⃗⃗ |.则正确的命题是___ ．11.（填空题.3分）如图.半径为R 的球O 的直径AB 垂直于平面α.垂足为B.△BCD 是平面α内边长为R 的正三角形.线段AC.AD 分别与球面交于点M 、N.则三棱锥A-BMN 的体积是___ ．12.（填空题.3分）在三棱锥A-BCD中.AC=AD=BC=BD=10.AB=8.CD=12.点P在侧面ACD上.且到直线AB的距离为√21 .则PB的取值范围是___ ．13.（单选题.3分）已知直线n⫋平面α.则m || n是m || α的（）A.充要条件B.充分非必要条件件C.必要非充分条件D.既非充分又非必要条件14.（单选题.3分）在正方体ABCD-A1B1C1D1中.E.F.G分别为棱1.A1B1的中点.用过点E.F.G的平面截正方体.则位于截面以下部分的几何体的侧（左）视图为（）A.B.C.D.15.（单选题.3分）中国有悠久的金石文化.印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体.但南北朝时期的官员独孤信的印信形状是“半正多面体”．半正多面体是由两种或两种以上的正多边形围成的多面体．半正多面体体现了数学的对称美.如图是一个棱数为24的半正多面体.它的所有顶点都在同一个正方体的棱上.且此正方体的棱长为1．则该半正多面.正确的有（）体：① 有12个顶点；② 有14个面；③ 表面积为3；④ 体积为56A. ① ② ③B. ② ③ ④C. ① ② ④D. ① ② ③ ④16.（单选题.3分）如图.已知正四面体A 1A 2A 3A 4.点A 5.A 6.A 7.A 8.A 9.A 10分别是所在棱中点.点P 满足 A 4P ⃗⃗⃗⃗⃗⃗⃗ =x A 4A 1⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ +y A 4A 2⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ +z A 4A 3⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ 且x+y+z=1.记| A 4Q ⃗⃗⃗⃗⃗⃗⃗⃗ |=| A 4P ⃗⃗⃗⃗⃗⃗⃗ |min .则当1≤i .j≤10且i≠j 时.数量积 A 4Q ⃗⃗⃗⃗⃗⃗⃗⃗ •A i A j ⃗⃗⃗⃗⃗⃗⃗⃗ 的不同取值的个数是（ ）A.3B.5C.9D.2117.（问答题.0分）设函数f （x ）=lg （x 2+2x-3）的定义域为集合A.函数g （x ）=a+ 1|x| -x 在[-3.-1]上存在零点时的a 的取值集合B ． （1）求A∩B ；（2）若集合C={x|x+2p≥0}.若x∈C 是x∈A 充分条件.求实数p 的取值范围．18.（问答题.0分）已知正方体ABCD-A 1B 1C 1D 1中的棱长为2.O 1是A 1C 1中点． （1）求证：AO 1 || 平面DBC 1；（2）设BB 1的中点为M.过A 、C 1、M 作一截面.并求出截面面积．19.（问答题.0分）设一正方形纸片ABCD边长为4厘米.切去阴影部分所示的四个全等的等腰三角形.剩余为一正方形纸片和四个全等的等腰三角形.沿虚线折起.恰好能做成一个正四棱锥（粘接损耗不计）.图中AH⊥PQ.O为正四棱锥底面中心．（1）若正四棱锥的棱长都相等.请求出它的棱长并画出它的直观图示意图；（2）设等腰三角形APQ的底角为x.试把正四棱锥的侧面积表示为x的函数.并求S范围．20.（问答题.0分）如图.在Rt△SOA中.∠OSA= π.斜边SA=4.半圆H的圆心H在边OS上.且与6SA相切.现将Rt△SOA绕SO旋转一周得到一个几何体.点B为圆锥底面圆周上一点.且∠AOB=90°．（1）求球H的半径；（2）求点O到平面SAB的距离；（3）设P是圆锥的侧面与球的交线上一点.求PO与平面SAB所成角正弦值的范围．21.（问答题.0分）设集合A的元素均为实数.若对任意a∈A.存在b∈B.c∈C．使得b+c=a且b-c=1.则称元素最少的B和C为A的“孪生集”；称A的“孪生集”的“孪生集”为A的“2级孪生集”；称A的“2级孪生集”的“孪生集”为A的“3级孪生集”.依此类推…（1）设A={3.5.7}.直接写出集合A的“孪生集”；（2）设元素个数为n的集合A的“孪生集”分别为B和C.若使集合∁B∪C（B∩C）中元素个数最少且所有元素之和为3.证明：A中所有元素之和为3n；（3）若A={a k|a k=a1+2（k-1）.1≤k≤n.k∈N*}.请直接写出A的“n级孪生集”的个数.设A的所有”n级孪生集”的并集为Ω.若Ω=M1∪M2∪M3；求有序集合组（M1.M2.M3）的个数．2019-2020学年上海市闵行区七宝中学高二（下）期末数学试卷参考答案与试题解析试题数：21.满分：01.（填空题.3分）已知集合A={（x.y ）|x 2+y 2=1}.B={（x.y ）|y=-x}.则A∩B 中元素的个数是___ ．【正确答案】：[1]2【解析】：解方程组 {x 2+y 2=1y =−x 即可得出A∩B 中的元素个数．【解答】：解：解 {x 2+y 2=1y =−x得. {x =−√22y =√22 或 {x =√22y =−√22.∴A∩B 元素的个数是2． 故答案为：2．【点评】：本题考查了描述法的定义.元素、集合的定义.交集的定义及运算.考查了计算能力.属于基础题．2.（填空题.3分）若平面α外的直线a 与平面α所成角为θ.则θ的取值范围是___ ． 【正确答案】：[1][0. π2 ]【解析】：当直线a || 平面α时.θ取最小值0.当直线a⊥平面α时.θ取最大值 π2 .当a 与平面α相交且不垂直时.θ∈（0. π2 ）.由此能求出θ的取值范围．【解答】：解：平面α外的直线a 与平面α所成角为θ. 当直线a || 平面α时.θ取最小值0. 当直线a⊥平面α时.θ取最大值 π2. 当a 与平面α相交且不垂直时.θ∈（0. π2 ）.∴平面α外的直线a 与平面α所成角为θ.则θ的取值范围是[0. π2 ]． 故答案为：[0. π2 ]．【点评】：本题考查线面角的取值范围的求法.考查空间中线面关系等基础知识.考查空间想象能力.是基础题．3.（填空题.3分）已知 AM ⃗⃗⃗⃗⃗⃗ =（0.1.2）. CN ⃗⃗⃗⃗⃗ =（1.0.2）.则直线AM 和CN 所成角的余弦值是___ ． 【正确答案】：[1] 45【解析】：利用向量夹角余弦函数公式直接求解．【解答】：解：设直线AM 和CN 所成角为θ. ∵ AM ⃗⃗⃗⃗⃗⃗ =（0.1.2）. CN ⃗⃗⃗⃗⃗ =（1.0.2）. ∴cosθ= |AM ⃗⃗⃗⃗⃗⃗ •CN ⃗⃗⃗⃗⃗⃗ ||AM ⃗⃗⃗⃗⃗⃗|•|CN ⃗⃗⃗⃗⃗⃗ | = √5•√5= 45 ． ∴直线AM 和CN 所成角的余弦值为 45 ． 故答案为： 45 ．【点评】：本题考查异面直线所成角的余弦值的求法.考查向量夹角余弦函数公式等基础知识.考查运算求解能力.是基础题．4.（填空题.3分）在北纬45°圈上有A 、B 两点.若该纬度圈上A 、B 两点间的劣弧长为 √24 πR （R 为地球的半径）.则A 、B 两点间的球面距离是___ ． 【正确答案】：[1] πR3【解析】：先求出北纬45°圈所在圆的半径.是A 、B 两地在北纬45°圈上对应的圆心角.得到线段AB 的长.设地球的中心为O.解三角形求出∠AOB 的大小.利用弧长公式求A 、B 这两地的球面距离．【解答】：解：北纬45°圈所在圆的半径为 √22 R.它们在纬度圈上所对应的劣弧长等于 √24 πR （R 为地球半径）.∴ √24 πR=θ× √22 R （θ是A 、B 两地在北纬45°圈上对应的圆心角）. 故θ= π2 .∴线段AB=R. ∴∠AOB= π3 .∴A 、B 这两地的球面距离是 πR3 . 故答案为： πR3 ．【点评】：本题考查球的有关经纬度知识.球面距离.弧长公式.考查空间想象能力.逻辑思维能力.是基础题．5.（填空题.3分）设x 、y 满足约束条件 {x +2y −2≥0x −y +1≥02x −y −4≤0 .则z=2x+y 的最大值是___ ．【正确答案】：[1]16【解析】：作出不等式组表示的平面区域.由z=2x+y 可得y=-2x+z.则z 表示直线y=-2x+z 在y 轴上的截距.截距越大.z 越大.结合图象即可求解z 的最大值．【解答】：解：作出x 、y 满足约束条件 {x +2y −2≥0x −y +1≥02x −y −4≤0 表示的平面区域.如图所示：由z=2x+y 可得y=-2x+z.则z 表示直线y=-2x+z 在y 轴上的截距.截距越大.z 越大作直线2x+y=0.然后把该直线向可行域平移. 当直线经过A 时.z 最大由 {x −y +1=02x −y −4=0 可得A （5.6）.此时z=16．故答案为：16．【点评】：本题主要考查了线性规划知识的应用.求解的关键是明确目标函数中z 的几何意义． 6.（填空题.3分）不等式mx 2-mx-2＜0对任意x∈R 恒成立的充要条件是m∈___ ． 【正确答案】：[1]（-8.0]【解析】：由不等式mx2-mx-2＜0对任意x∈R恒成立.得m=0或{m≠0(−m)2+8m＜0 .由此能求出不等式mx2-mx-2＜0对任意x∈R恒成立的充要条件．【解答】：解：∵不等式mx2-mx-2＜0对任意x∈R恒成立.∴m=0或{m≠0(−m)2+8m＜0 .解得-8＜m≤0．∴不等式mx2-mx-2＜0对任意x∈R恒成立的充要条件是m∈（-8.0]．故答案为：（-8.0]．【点评】：本题考查充分条件、必要条件、充要条件的判断.考查函数性质等基础知识.考查运算求解能力.是基础题．7.（填空题.3分）某圆柱的高为2.底面周长为16.其三视图如图.圆柱表面上的点M在正（主）视图上的对应点为A.圆柱表面上的点N在侧（左）视图上的对应点为B.则在此圆柱侧面上.从M到N的路径中.最短路径的长度为 ___ ．【正确答案】：[1]2 √5【解析】：判断三视图对应的几何体的形状.利用侧面展开图.转化求解即可．【解答】：解：由题意可知几何体是圆柱.底面周长16.高为：2.直观图以及侧面展开图如图：圆柱表面上的点N在左视图上的对应点为B.则在此圆柱侧面上.从 M到N的路径中.最短路径的长度：√22+42=2√5．故答案为：2√5．【点评】：本题考查三视图与几何体的直观图的关系.侧面展开图的应用.考查计算能力.属于中档题．8.（填空题.3分）有一多边形ABCD 水平放置的斜二测直观图A′B′C′D′是直角梯形（如图所示）.其中∠A'B′C′=45°.B′C′⊥C′D′.A′D′=D′C′=1.则原四边形ABCD 的面积为___ ．【正确答案】：[1]3 √2【解析】：由四边形ABCD 水平放置的直观图得出四边形ABCD 的各边关系.再求四边形ABCD 的面积．【解答】：解：四边形ABCD 水平放置的直观图是直角梯形. 且∠A'B'C'=45°.A'D'=D'C'=1.D'C'⊥B'C'. 所以B′C′=2A′D′=2.A′B′= √2 ；所以四边形ABCD 中.AB=2A′B′=2 √2 .AD=A′D′=1.BC=B′C′=2. 且AB⊥BC .AD || BC.所以四边形ABCD 的面积为S= 12×（1+2）×2 √2 =3 √2 ． 故答案为：3 √2 ．【点评】：本题考查了水平放置的直观图性质等应用问题.也考查了运算求解能力.是基础题． 9.（填空题.3分）正四棱柱ABCD-A 1B 1C 1D 1中.AB=AD=1.E 为BB 1中点.若点P 满足 AP ⃗⃗⃗⃗⃗ = λPD ⃗⃗⃗⃗⃗ .且BP || 平面AED 1.则λ=___ ． 【正确答案】：[1]1【解析】：先猜想点P 为AD 的中点.取AD 1的中点F.连接EF 、PF.再证明BP || 平面AED 1．结合正四棱柱和中位线的性质可推出四边形BPFE 为平行四边形.从而BP || EF.然后由线面平行的判定定理可证得BP || 平面AED 1．【解答】：解：如图所示.分别取AD 1、AD 的中点F 、P.连接EF 、PF.此点P 即为所求．理由如下：∵F 、P 分别为AD 1、AD 的中点.∴FP || D 1D.FP= 12 D 1D.∵E 为BB 1中点.∴BE= 12 BB 1.又D 1D || BB 1.∴FP || BE .FP=BE.∴四边形BPFE 为平行四边形.∴BP || EF .∵BP⊄平面AED 1.EF⊂平面BPFE.∴BP || 平面AED 1．由于P 为AD 的中点.所以λ=1．故答案为：1．【点评】：本题考查空间中线与面的平行关系.对于找点问题.一般可采用先猜后证的思想.熟练掌握线面平行的判定定理是解题的关键.考查学生的空间立体感、逻辑推理能力.属于中档题．10.（填空题.3分）在正方体ABCD-A 1B 1C 1D 1中.给出下面四个命题： ① （ A 1A ⃗⃗⃗⃗⃗⃗⃗ + A 1D 1⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ +A 1B 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ ）2=3（ A 1A ⃗⃗⃗⃗⃗⃗⃗ ）2； ② AD 1⃗⃗⃗⃗⃗⃗⃗ 与 A 1B ⃗⃗⃗⃗⃗⃗⃗ 夹角为120°； ③ A 1C ⃗⃗⃗⃗⃗⃗⃗ •C 1D ⃗⃗⃗⃗⃗⃗⃗ =0； ④ 正方体的体积是| AB ⃗⃗⃗⃗⃗ • BC ⃗⃗⃗⃗⃗ • CC 1⃗⃗⃗⃗⃗⃗⃗ |.则正确的命题是___ ．【正确答案】：[1] ① ② ③【解析】：通过空间向量的运算以及向量的模.判断 ① 的正误；利用建立空间直角坐标系.求解向量的夹角判断 ② 的正误；利用空间向量的数量积判断 ③ 的正误；利用向量的数量积的值判断 ④ 的正误；【解答】：解：在正方体ABCD-A 1B 1C 1D 1中.设正方体的棱长为1.对于 ① （ A 1A ⃗⃗⃗⃗⃗⃗⃗ + A 1D 1⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ + A 1B 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ ）2=（ A 1C ⃗⃗⃗⃗⃗⃗⃗ ）2= |A 1C ⃗⃗⃗⃗⃗⃗⃗ |2 =3.3（ A 1A ⃗⃗⃗⃗⃗⃗⃗ ）2=3.所以 ① 正确；② 建立如图所示的坐标系.则 AD 1⃗⃗⃗⃗⃗⃗⃗ =（-1.0-1）. A 1B ⃗⃗⃗⃗⃗⃗⃗ =（0.1.-1）.AD 1⃗⃗⃗⃗⃗⃗⃗ 与 A 1B ⃗⃗⃗⃗⃗⃗⃗ 夹角的余弦函数值为 A 1B ⃗⃗⃗⃗⃗⃗⃗⃗ •AD 1⃗⃗⃗⃗⃗⃗⃗⃗ |A 1B ⃗⃗⃗⃗⃗⃗⃗⃗ ||AD 1⃗⃗⃗⃗⃗⃗⃗⃗ | = −1√2×√2=- 12 . 所以 AD 1⃗⃗⃗⃗⃗⃗⃗ 与 A 1B ⃗⃗⃗⃗⃗⃗⃗ 夹角为120°.所以 ② 正确；③ A 1C ⃗⃗⃗⃗⃗⃗⃗ •C 1D ⃗⃗⃗⃗⃗⃗⃗ =（-1.1.-1）•（0.-1.-1）=0.所以 ③ 正确；④ | AB ⃗⃗⃗⃗⃗ • BC ⃗⃗⃗⃗⃗ • CC 1⃗⃗⃗⃗⃗⃗⃗ |= |0•CC 1⃗⃗⃗⃗⃗⃗⃗ | =0.所以正方体的体积是| AB ⃗⃗⃗⃗⃗ • BC ⃗⃗⃗⃗⃗ • CC 1⃗⃗⃗⃗⃗⃗⃗ |.不正确；故答案为： ① ② ③ ．【点评】：本题考查命题的真假.空间向量的坐标运算以及数量积的应用.夹角的求法.考查计算能力． 11.（填空题.3分）如图.半径为R 的球O 的直径AB 垂直于平面α.垂足为B.△BCD 是平面α内边长为R 的正三角形.线段AC.AD 分别与球面交于点M 、N.则三棱锥A-BMN 的体积是___ ．【正确答案】：[1] 8√375 R 3【解析】：AB=2R.BC=R.AC= √5 R.△BCD 是平面α内边长为R 的正三角形.ABC∽△AMB . AM AC =45 .类似有 AN AD = 45 . V A−BMN V A−BCD = S △AMN S △ABC =（ 45 ）2.由此能求出三棱锥A-BMN 的体积．【解答】：解：∵AB=2R .BC=R.AC= √5 R.半径为R 的球O 的直径AB 垂直于平面α.垂足为B.△BCD 是平面α内边长为R 的正三角形. 线段AC.AD 分别与球面交于点M 、N.∴∠BAM=∠BAC.∠AMB=∠ABC=90°. ∴△ABC∽△AMB.∴ AB AM = ACAB.∴A M= 4√55R .∴ AMAC =45.类似有ANAD= 45.∴ V A−BMN V A−BCD = S△AMNS△ABC=（45）2= 1625.∴三棱锥A-BMN的体积：V A-BMN= 1625×13×√34×R2×2R = 8√375R3．故答案为：8√375R3．【点评】：本题考查三棱锥的体积的求法.考查球、三棱锥的结构特征等基础知识.考查运算求解能力.是中档题．12.（填空题.3分）在三棱锥A-BCD中.AC=AD=BC=BD=10.AB=8.CD=12.点P在侧面ACD上.且到直线AB的距离为√21 .则PB的取值范围是___ ．【正确答案】：[1][ √92−16√7 . √57 ]【解析】：由题意画出图形.可知P的轨迹.求出tan∠PAB的范围.得到AH.BH的范围.再由勾股定理求解BP的范围．【解答】：解：如图.∵P 到直线AB 的距离为 √21 为定值.∴P 在以AB 为轴.底面半径为 √21 的圆柱的侧面上. 由题设条件可知.P 的轨迹为侧面ACD 与圆柱侧面的交线.是椭圆的一部分．（平面ACD 与轴AB 不垂直.该平面与圆柱侧面的交线为椭圆）．如图设CD 的中点为M.连接AM.BM.由AC=AD=BC=BD=10.CD=12.知AM⊥CD .BM⊥CD .且AM=BM=8．连接AP 并延长交CD 于Q.连接BQ.则AQ=BQ ．∴cos∠BAQ= 12AB AQ =4AQ. ∵AM≤AQ≤AC .即8≤AQ≤10.∴cos∠BAQ= 4AQ ∈（ 25，12）.则tan∠BAQ∈[ √3 . √212 ]． 过P 作PH⊥AB 于H.则PH= √21 ．∴AH= PH tan∠BAQ ∈[2. √7 ].则BH∈[8- √7 .6].∴PB= √BH 2+PH 2 ∈[ √92−16√7 . √57 ]．故答案为：[ √92−16√7 . √57 ]．【点评】：本题考查空间中点、线、面间的距离计算.考查空间想象能力与思维能力.考查运算求解能力.是中档题．13.（单选题.3分）已知直线n ⫋平面α.则m || n 是m || α的（ ）A.充要条件B.充分非必要条件件C.必要非充分条件D.既非充分又非必要条件【正确答案】：D【解析】：直线n⫋平面α.则m || n⇒m || α或m⊂α.m || α⇒m与n平行或异面．【解答】：解：直线n⫋平面α.则m || n⇒m || α或m⊂α.m || α⇒m与n平行或异面.∴m || n是m || α的既非充分又非必要条件．故选：D．【点评】：本题考查充分条件、必要条件、充要条件的判断.考查线面平行、线面平行的性质等基础知识.考查空间想象能力.是基础题．14.（单选题.3分）在正方体ABCD-A1B1C1D1中.E.F.G分别为棱1.A1B1的中点.用过点E.F.G的平面截正方体.则位于截面以下部分的几何体的侧（左）视图为（）A.B.C.D.【正确答案】：C【解析】：首先求出截面的图形.进一步利用三视图求出结果．【解答】：解：正方体被经过E、F、G点的平面所截.其中左边的正方形的左上顶点A被切去.故少一个角.右下面留一个斜棱.故左视图为C．故选：C ．【点评】：本题考查的知识要点：三视图的应用．15.（单选题.3分）中国有悠久的金石文化.印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体.但南北朝时期的官员独孤信的印信形状是“半正多面体”．半正多面体是由两种或两种以上的正多边形围成的多面体．半正多面体体现了数学的对称美.如图是一个棱数为24的半正多面体.它的所有顶点都在同一个正方体的棱上.且此正方体的棱长为1．则该半正多面体： ① 有12个顶点； ② 有14个面； ③ 表面积为3； ④ 体积为 56 .正确的有（ ）A. ① ② ③B. ② ③ ④C. ① ② ④D. ① ② ③ ④【正确答案】：C 【解析】：由图形即可判断 ① ② ；由半正多面体的所有顶点都在同一个正方体的棱上.可得正方形和正三角形的边长.计算即可判断 ③ ；利用割补法计算可得半正多面体的体积.即可判断 ④ ．【解答】：解：由图形可得该半正多面体共有12个顶点.14个面.故 ① ② 正确； 半正多面体的所有顶点都在同一个正方体的棱上.且此正方体的棱长为1.可得该半正多面体所有顶点都为正方体的棱的中点.所以该半正多面体的棱长为 √22 .故半正多面体的面积为6× √22 × √22 +8× √22 × √22× sin60°=3+2 √3 .故 ③ 错误；半正多面体的体积为1-8× 13 × 12 × 12 × 12 × 12 = 56 .故 ④ 正确．故选：C ．【点评】：本题考查正方体的切割后的多面体的性质.属于中档题．16.（单选题.3分）如图.已知正四面体A 1A 2A 3A 4.点A 5.A 6.A 7.A 8.A 9.A 10分别是所在棱中点.点P 满足 A 4P ⃗⃗⃗⃗⃗⃗⃗ =x A 4A 1⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ +y A 4A 2⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ +z A 4A 3⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ 且x+y+z=1.记| A 4Q ⃗⃗⃗⃗⃗⃗⃗⃗ |=| A 4P ⃗⃗⃗⃗⃗⃗⃗ |min .则当1≤i .j≤10且i≠j 时.数量积 A 4Q ⃗⃗⃗⃗⃗⃗⃗⃗ •A i A j ⃗⃗⃗⃗⃗⃗⃗⃗ 的不同取值的个数是（ ）A.3B.5C.9D.21【正确答案】：B 【解析】：先根据空间向量四点共面的向量表达式得到点P 在平面A 1A 2A 3内.又由 A 4Q ⃗⃗⃗⃗⃗⃗⃗⃗ |=| A 4P ⃗⃗⃗⃗⃗⃗⃗ |min 可得到 A 4Q ⃗⃗⃗⃗⃗⃗⃗⃗ ⊥平面A 1A 2A 3.再结合向量数量积的几何意义即可求解．【解答】：解：∵点P 满足 A 4P ⃗⃗⃗⃗⃗⃗⃗ =x A 4A 1⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ +y A 4A 2⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ +z A 4A 3⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ 且x+y+z=1.∴点P 在平面A 1A 2A 3内.由| A 4Q ⃗⃗⃗⃗⃗⃗⃗⃗ |=| A 4P ⃗⃗⃗⃗⃗⃗⃗ |min .可得 A 4Q ⃗⃗⃗⃗⃗⃗⃗⃗ ⊥平面A 1A 2A 3.由向量数量积的几何意义.A i A j 在 A 4Q 的投影有 5 种情况： 0，±12|A 4Q ⃗⃗⃗⃗⃗⃗⃗⃗ |，±|A 4Q ⃗⃗⃗⃗⃗⃗⃗⃗ .∴ 数量积 A 4Q •A i A j ⃗⃗⃗⃗⃗⃗⃗⃗ 的不同取值的个数是 5．故选：B ．【点评】：本题考查空间向量四点共面的向量表达式.向量数量积的几何意义.难点在意将数量积转化为几何意义来解题.属于难题．17.（问答题.0分）设函数f （x ）=lg （x 2+2x-3）的定义域为集合A.函数g （x ）=a+ 1|x| -x 在[-3.-1]上存在零点时的a 的取值集合B ．（1）求A∩B ；（2）若集合C={x|x+2p≥0}.若x∈C 是x∈A 充分条件.求实数p 的取值范围．【正确答案】：【解析】：（1）先分别求出集合A.B.由此能求出A∩B ．（2）求出集合C={x|x+2p≥0}={x|x≥-2p}.由x∈C 是x∈A 充分条件.得到C⊆A .由此能求出实数p 的取值范围．【解答】：解：（1）∵函数f （x ）=lg （x 2+2x-3）的定义域为集合A.∴A={x|x 2+2x-3＞0}={x|x ＜-3或x ＞1}.∵函数g （x ）=a+ 1|x| -x 在[-3.-1]上存在零点时的a 的取值集合B.g （x ）=a+ 1|x| -x 在[-3.-1]有解.∴a=x - 1|x| =x+ 1x ∈[- 103 .-2].∴B=[- 103 .-2].∴A∩B=[- 103 .-3）．（2）∵集合C={x|x+2p≥0}={x|x≥-2p}.x∈C 是x∈A 充分条件.∴C⊆A .∴-2p ＞1.解得p ＜−12 ．∴实数p 的取值范围是（-∞.- 12 ）．【点评】：本题考查交集、实数的取值范围的求法.考查函数性质、交集定义、充分条件等基础知识.考查运算求解能力.是基础题．18.（问答题.0分）已知正方体ABCD-A 1B 1C 1D 1中的棱长为2.O 1是A 1C 1中点．（1）求证：AO 1 || 平面DBC 1；（2）设BB 1的中点为M.过A 、C 1、M 作一截面.并求出截面面积．【正确答案】：【解析】：（1）连接AC.BD.设AC∩BD=O.连接OC1.证明四边形AOC1O1为平行四边形.得AO1 || C1O.再由直线与平面平行的判定.得到C1O⊂平面DBC1.（2）找出过A、C1、M的平面截正方体的截面图形.再由三角形面积公式求解．【解答】：解：（1）证明：如图.连接AC.BD.设AC∩BD=O.连接OC1.由AA1 || CC1.AA1=CC1可得四边形AA1C1C为平行四边形.则AC || A1C1.又C1O1=AO.∴四边形AOC1O1为平行四边形.得AO1 || C1O．而A1O⊄平面DBC1.C1O⊂平面DBC1.∴AO1 || 平面DBC1；（2）连接AM.C1M.设平面AMC1与平面AA1D1D交于AN.由平面AA1D1D || 平面BB1C1C.且平面AMC1∩平面BB1C1C=C1M.平面AMC1∩平面AA1D1D=AN.∴C1M || AN．同理可得AM || C1N.得到四边形AMC1N为平行四边形.在Rt△ABM与Rt△C1B1N中.求得AM=C1M.即四边形AMC1N为菱形.得N为DD1的中点．∵正方体ABCD-A1B1C1D1的棱长为2.∴MN= 2√2 .AC1=√22+22+22=2√3．∴截面面积S= 1×2√2×2√3=2√6．2【点评】：本题考查直线与平面平行的判定.考查空间想象能力与运算求解能力.是中档题．19.（问答题.0分）设一正方形纸片ABCD边长为4厘米.切去阴影部分所示的四个全等的等腰三角形.剩余为一正方形纸片和四个全等的等腰三角形.沿虚线折起.恰好能做成一个正四棱锥（粘接损耗不计）.图中AH⊥PQ.O为正四棱锥底面中心．（1）若正四棱锥的棱长都相等.请求出它的棱长并画出它的直观图示意图；（2）设等腰三角形APQ的底角为x.试把正四棱锥的侧面积表示为x的函数.并求S范围．【正确答案】：a .结合【解析】：（1）设出正四棱锥的棱长a.正方形纸片ABCD边长为4厘米.可得AH= √32正四棱锥的棱长都相等.即可求解a的值.（2）设PH=b.值AH=btanx.由2atanx+2a=4 √2 .即可得a.在表示出正四棱锥的侧面积S.利用基本不等式即可S范围.a . 【解答】：解：（1）设出正四棱锥的棱长a.正方形纸片ABCD边长为4厘米.可得AH= √32a+a=AC=4√2 .∵正四棱锥的棱长都相等.即2×√32∴ a=2√6−2√2．故得正四棱锥的棱长为2√6−2√2；（2）由题意.设PH=b.则AH=btanx.由2atanx+2a=4 √2 . 可得a= 2√2tanx+1.从而侧面积S= 4×12×PO•AH=2a2•tanx = 16tanx(tanx+1)2.其中tanx∈（1.+∞）；∴S= 16tanx+1tanx +2∈（0.4）.故得S范围是（0.4）．【点评】：本题主要考查了正四棱锥的几何性质.正四棱锥中的棱长、高、体积的计算.建立函数模型并求其最值的方法.有一定的难度．20.（问答题.0分）如图.在Rt△SOA中.∠OSA= π6.斜边SA=4.半圆H的圆心H在边OS上.且与SA相切.现将Rt△SOA绕SO旋转一周得到一个几何体.点B为圆锥底面圆周上一点.且∠AOB=90°．（1）求球H的半径；（2）求点O 到平面SAB 的距离；（3）设P 是圆锥的侧面与球的交线上一点.求PO 与平面SAB 所成角正弦值的范围．【正确答案】：【解析】：（1）令SA 与圆切于K.则有SO=3r.即可求解．（2）由等体积法得V O-SAB =V S-OAB ⇒ 13S △SAB •d =13S △OAB •SO .即可得点O 到平面SAB 的距离；（3）如图建立空间直角坐标系.求得平面SAB 的法向量 n ⃗ =(x ，y ，z) .设PO 与平面SAB 所成角为α.则sinα= |PO ⃗⃗⃗⃗⃗ •n ⃗ ||PO ⃗⃗⃗⃗⃗ |•|n ⃗ | = |√6sin(θ+π4)+√3|2√7【解答】：解：（1）如图.令SA 与圆切于K.∵∠OSA= π6 .∴SH=2r .（r 为球半径）∴SO=3r .∵在Rt△SOA 中.∠OSA= π6 .斜边SA=4.∴SO=2 √3 .OA=2.∴r= SO3=2√33． （2）由等体积法.V O-SAB =V S-OAB ⇒ 13S △SAB •d =13S △OAB •SO .∵S △SAB = 12AB •√SA 2−(AB 2)2= 12×2√2•√16−2=2√7 .S △OAB =2. ∴d= 2√217 .即点O 到平面SAB 的距离为 2√217； （3）如图建立空间直角坐标系.则A （0.2.0）.B （2.0.0）.S （0.0.2 √3 ）.P （cosθ.sinθ. √3 ）. SA ⃗⃗⃗⃗⃗ =(0，2，−2√3) . SB ⃗⃗⃗⃗⃗ =(2，0，−2√3 ）. PO ⃗⃗⃗⃗⃗ =(−cosθ，−sinθ，−√3) .设平面SAB 的法向量 n ⃗ =(x ，y ，z) .由 {SA ⃗⃗⃗⃗⃗ •n ⃗ =0SB ⃗⃗⃗⃗⃗ •n ⃗ =0 ⇒ {y =√3z x =√3z∴ n ⃗ =(√3，√3，1) . 设PO 与平面SAB 所成角为α.则sinα= |PO ⃗⃗⃗⃗⃗ •n ⃗ ||PO ⃗⃗⃗⃗⃗ |•|n ⃗ | = |√6sin(θ+π4)+√3|2√7 . √6+√32√7 ]. ∴PO 与平面SAB 所成角正弦值的范围为：[0.√42+√2114 ]．【点评】：本题考查了空间几何体内切球问题、线面角求解.考查了数学运算、直观想象等核心素养.属于中档题．21.（问答题.0分）设集合A的元素均为实数.若对任意a∈A.存在b∈B.c∈C．使得b+c=a且b-c=1.则称元素最少的B和C为A的“孪生集”；称A的“孪生集”的“孪生集”为A的“2级孪生集”；称A的“2级孪生集”的“孪生集”为A的“3级孪生集”.依此类推…（1）设A={3.5.7}.直接写出集合A的“孪生集”；（2）设元素个数为n的集合A的“孪生集”分别为B和C.若使集合∁B∪C（B∩C）中元素个数最少且所有元素之和为3.证明：A中所有元素之和为3n；（3）若A={a k|a k=a1+2（k-1）.1≤k≤n.k∈N*}.请直接写出A的“n级孪生集”的个数.设A的所有”n级孪生集”的并集为Ω.若Ω=M1∪M2∪M3；求有序集合组（M1.M2.M3）的个数．【正确答案】：【解析】：（1）根据集合定义直接得到答案；（2）将集合 A 中元素从小到大排列：a1＜a2＜…＜a n.则“孪生集” B={a1+12，a2+12，…，a n+1 2} . C={a1−12，a2−12，…，a n−12} .a1.a2.….a n构成公差为 2 的等差数列.计算得到答案；（3）A 的“n级孪生集”的个数为 2n.计算元素个数得到答案．【解答】：解：（1）B={2.3.4}.C={1.2.3}；（2）将集合 A 中元素从小到大排列：a1＜a2＜…＜a n.则其“孪生集“ B={a1+12，a2+12，…，a n+12} . C={a1−12，a2−12，…，a n−12} .设集合D=∁（B∪C）（B∩C）.由于a1−12∈C，a1−12∉B，a n+12∈B，a n+12∉C .因此集合 D 中元素个数card（D）≥2.若card（D）=2.则有a k+12=a k+1−12(1≤k≤n−1) .即a k+1-a k=2（1≤k≤n-1）.因此a1.a2.….a n构成公差为 2 的等差数列.D={a1−12，a n+12} .所以a1−12+a n+12=a1+a n2=3 .进而a1+a2+⋯+a n=(a1+a n)n2=3n．（3）A 的“n 级孪生集”的个数为 2n.A 所有“n 级孪生集”的并集Ω 的元素个数为 2n+n-1.每个元素至少属于 M1.M2.M3中的一个.所以有序集合组（M1.M2.M3）的个数为(23−1)2n+n−1=72n+n−1．【说明】由（2）知.A 所有“1 级孪生集”为B={a1+12，a1+32，…，a1+2n−12}，C={a1−12，a1+1 2，…，a1+2n−32} .它们的并集Ω={a1−12，a1+12，…，a1+2n−32，a1+2n−12}有 n+1=21+n-1 个元素；A 所有“2 级孪生集“为{a1+34，a1+54，…，a1+2n+14}，{a1−14，a1+14，…，a1+2n−34} . {a1+14，a1+3 4，…，a1+2n−14}，{a1−34，a1−14，…，a1+2n−54} .它们的并集Ω={a1−34，a1−14，…，a1+2n−14，a1+2n+14} .有 n+3=22+n-1 个元素；A 所有“3 级孪生集“为{a1+78，a1+98，…，a1+2n+58}，{a1−18，a1+18，…，a1+2n−38} .{a1+38，a1+58，…，a1+2n+18}，{a1−58，a1−38，…，a1+2n−78} .{a1+58，a1+78，…，a1+2n+38}，{a1−38，a1−18，…，a1+2n−58} .{a1+18，a1+38，…，a1+2n+18}，{a1−78，a1−58，…，a1+2n−98} .它们的并集Ω={a1−78，a1−58，…，a1+2n+38，a1+2n+58} .有 n+7=23+n-1个元素；A 所有“n 级孪生集“的并集Ω={a1−(2n−1)2n ，a1−(2n−3)2n，…，a1+2n+(2n−3)2n} .其中第 2 个元素的分子和最大元素的分子和恰为2a1+2n.即所有元素从小打到大构成首项为a1−(2n−1)2n .公差为12n−1的等差数列.所以共有a1+2n+(2n−3)2n−a1−(2n−1)2n12n−1+1=2n+n−1项.也即A所有“n 级孪生集”的并集Ω 的元素个数为 2n+n-1．【点评】：本题考查集合的定义.集合元素的个数和元素和.已在考查学生的应用能力.属于难题．。

2019-2020学年上海闵行区七宝中学高二下学期期中数学试卷一、单选题（本大题共4小题，共12.0分）1.某校在一年一度的“校园十佳歌手”比赛中，9位评委为参赛选手A给出的分数的茎叶图如图所示．在去掉一个最高分和一个最低分后，得出选手A得分的中位数是()A. 93B. 92C. 91D. 902.如图所示，AB是⊙O的直径，VA垂直于⊙O所在的平面，点C是圆周上不同于A，B的任意一点，M，N分别为VA，VC的中点，则下列结论正确的是()A. MN//ABB. MN与BC所成的角为45°C. OC⊥平面VACD. 平面VAC⊥平面VBC3.甲、乙、丙三名毕业生参加某公司人力资源部安排的面试，三人依次进行，每次一人，其中甲、乙两人相邻的概率为A. B. C. D.4.已知z1≠−1，z1−1z1+1=bi(b∈R)，z=4(z1+1)2−1，则z对应的点在()A. 圆上B. 抛物线上C. 双曲线上D. 椭圆上二、单空题（本大题共12小题，共36.0分）5.已知集合={直线}，={平面}，.若，给出下列四个命题：①②③④其中所有正确命题的序号是．6.已知(x+1x)9展开式中x5的系数是______；7. 两人射击命中目标的概率分别为现两人同时射击目标，则目标能被命中的概率为。

(用数字作答)8. 如图，在直角梯形ABCD 中，AD//BC ，AD =12BC =2，∠ABC =90°，∠C =45°，E 为BC 中点，现将△CDE 沿DE 折起，使得平面CDE ⊥平面ABED ，连接AC 、BC ，设M 为CE 中点，动点P 在平面CBE 和平面CDE 上运动，且始终满足AM ⊥MP ，则点P 形成的轨迹长度为______．9.10. 在(2x −1√x )5的展开式中，x 2的系数为______．11. 某学生参加2门选修课的考试．假设该学生第一门、第二门课程取得A 的概率依次为45、35，且不同课程是否取得A 相互独立．则该生只取得一门课程A 的概率为______ 12. 给出下列命题：①若f′(x 0)=0，则函数f(x)在x =x 0处有极值； ②m >0是方程x 2m+y 24=1表示椭圆的充要条件；③若f(x)=(x 2−8)e x ，则f(x)的单调递减区间为(−4,2)； ④双曲线x 2a 2−y 2b 2=1的离心率为e 1，双曲线x 2b 2−y 2a 2=1的离心率为e 2，则e 1+e 2的最小值为2√2 其中为真命题的序号是______ ．13. 已知f(x +1)=x 2+2x +3，则f(2)的值为______．14. 第一排有5个座位，安排4个老师坐下，其中老师A 必须在老师B 的左边，共有______ 种不同的排法(结果用数字表示)．15. 周五下午，我们1，2两个班的课分别都是语文，数学，物理，和自习．由于我们两个班的语文，数学，物理老师都一样的，即同一时间，某位老师只能在其中一个班上课，现教务处有______种排课方案．16. 已知集合M ={x||x|<1}，N ={a}，若M ∪N =M ，则实数a 的取值范围是______ ．三、解答题（本大题共5小题，共60.0分）17.已知(1−x+x2)7=a0+a1x+a2x2+⋯+a14x14.求：(1)a0+a1+a2+⋯+a14．(2)a1+a3+a5+⋯+a13．18.如图，在四棱锥P−ABCD中，底面是边长为2的菱形，且∠BAD=120°，且PA⊥平面ABCD，PA=，M，N分别为PB，PD的中点．(1)证明：MN//平面ABCD；(2)过点A作AQ⊥PC，垂足为点Q，求二面角A−MN−Q的平面角的余弦值．19.(本小题满分12分)已知四棱锥的底面为直角梯形，，底面，且，，是的中点。