走进图形世界复习

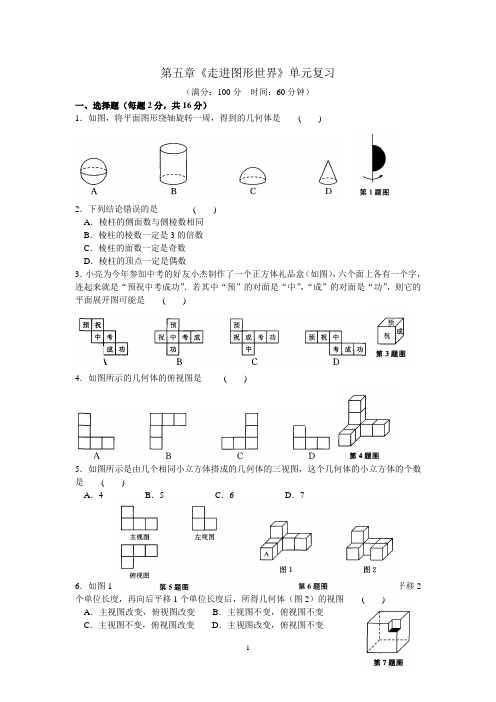
第五章《走进图形世界》单元复习（满分：100分时间：60分钟）一、选择题（每题2分，共16分）1．如图，将平面图形绕轴旋转一周，得到的几何体是( )2．下列结论错误的是( )A．棱柱的侧面数与侧棱数相同B．棱柱的棱数一定是3的倍数C．棱柱的面数一定是奇数D．棱柱的顶点一定是偶数3．小亮为今年参加中考的好友小杰制作了一个正方体礼品盒（如图），六个面上各有一个字，连起来就是“预祝中考成功”．若其中“预”的对面是“中”，“成”的对面是“功”，则它的平面展开图可能是( )4．如图所示的几何体的俯视图是( )5．如图所示是由几个相同小立方体搭成的几何体的三视图，这个几何体的小立方体的个数是( )A．4 B．5 C．6 D．76．如图1所示是由6个棱长为1个单位长度的正方体摆放而成的，将正方体A向右平移2个单位长度，再向后平移1个单位长度后，所得几何体（图2）的视图( )A．主视图改变，俯视图改变B．主视图不变，俯视图不变C．主视图不变，俯视图改变D．主视图改变，俯视图不变7．如图，从边长为10的正方体的一顶点处挖去一个边长为1的小正方体，剩下图形的表面积为( )A．600 B．599 C．598 D．5978．两个完全相同的长方体的长、宽、高分别为3，2，1，把它们叠放在一起组成一个新的长方体，在这些新长方体中，表面积的最小值为( )A．42 B．38 C．20 D．32二、填空题（每题2分，共20分）9．直角三角尺绕它的一条直角边旋转一周，形成一个_______体；一枚硬币在桌面上竖直快速转动，形成一个_______体．10.若一个正多面体有20个顶点，12个面，则它共有_______条棱．11.如图所示是某个几何体的展开图，这个几何体是_______．12.以上三组图形都是由四个等边三角形组成的，其中能折成多面体的是_______．（填序号）13.如图所示的图形可以折成一个长方体，该长方体的表面积为_______cm2.14.如图所示是一个正方体盒的展开图，若在其中的三个正方形A，B，C内分别填入适当的数，使得折成正方体后相对面上的两个数互为相反数，则填人正方形中A，B，C内的三个数依次为_______，_______，_______．15.如图所示是由一些相同的小立方体搭成的几何体，在其三种视图中，面积较小的是_______视图．16.有一个正方体的六个面上分别标有数字1，2，3，4，5，6，从三个不同的角度观察这个正方体所得到的结果如图所示，如果标有数字6的面所对面上的数字记为a，标有数字2的面所对面上的数字记为b，那么a＋b的值为_______．17.如图所示为一个无盖长方体盒子的展开图（重叠部分不计），根据图中数据，可知该无盖长方体的容积为_______．18.若由一些完全相同的小正方体搭成的几何体的主视图和左视图如图所示，则组成这个几何体的小正方体的个数可能是_______．三、解答题（共64分）19.（本题10分）把图中图形绕虚线旋转一周，指出所得几何体与下面A～E中几何体的对应关系．20.（本题12分）如图，小华用若干个正方形和长方形准备拼成一个长方体的展开图．拼完后，小华看来看去总觉得所拼图形似乎存在问题．(1)请你帮小华分析一下拼图是否存在问题：若有多余块，则把图中多余部分涂黑；若还缺少，则直接在原图中补全．(2)若图中的正方形边长为2cm，长方形的长为3cm，宽为2cm，请直接写出修正后所折叠而成的长方体的容积：_______cm3．21．（本题8分）如图所示是一个几何体，请画出它的三视图．22.（本题10分）一个小立方体的六个面分别标有字母A，B．C，D，E，F，从三个不同方向看到的情形如图所示．(1)A对面的字母是_______，B对面的字母是_______，E对面的字母是_______．（请直接填写答案）(2)若A＝2x－1，B＝－3x＋9，C＝－5，D＝1，E＝4x＋5，F＝9，且字母A与它对面的字母表示的数互为相反数，求B，E的值．23.（本题12分）由几个相同的边长为1的小立方块搭成的几何体的俯视图如下图所示，格中的数字表示该位置的小立方块的个数．(1)请在上面方格纸中分别画出这个几何体的主视图和左视图；(2)根据三视图，这个组合几何体的表面积为_______个平方单位；（包括底面积）(3)若上述小立方块搭成的几何体的俯视图不变，各位置的小立方块个数可以改变（总数目不变），则搭成的这样的组合几何体的表面积最大为_______个平方单位．（包括底面积）24．（本题12分）18世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式，被称为欧拉公式．请你观察下列几种简单多面体模型，解答下列问题：(1)根据上面多面体模型，完成表格中的空格：你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是_______．(2)一个多面体的面数比顶点数大8，且有30条棱，则这个多面体的面数是_______．(3)某个玻璃饰品的外形是简单多面体，它的外表面由三角形和八边形两种多边形拼接而成，且有24个顶点，每个顶点处都有3条棱，设该多面体外表面三角形的个数为x，八边形的个数为y个，求x＋y的值．参考答案一、选择题1.A2.C3.C4.B5.B6.C7.A8.D二、填空题9．圆锥球10．30 11．三棱柱12．①③13．88 14．1 0 2 15．主16．7 17．6 18．4或5或6或7三、解答题19．(1)↔B，(2) ↔C，(3) ↔D，(4) ↔A，(5) ↔E20．(1)如图(2)1221．如图22．(1)C D F (2)1723．(1)主视图和左视图分别如下：(2)24(3)2624．(1)6 6 E＝V＋F－2 (2)20 (3)14。

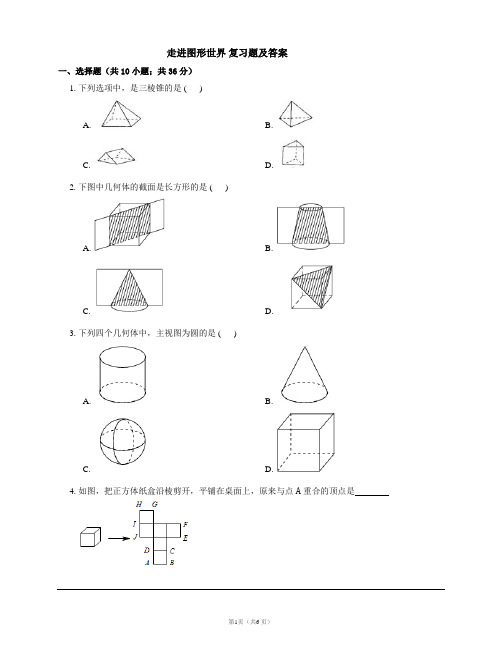
第5章走进图形世界一立体图形、图形的变化一、知识点复习及例题选讲1知识点1 :常见立体图形的认识与分类例1、如图3.1-1，将下列图形与对应的图形名称用线连接起来:例2、埃及金字塔类似于几何体A 、圆锥B 、圆柱C 、棱锥D 、棱柱2、知识点2 :点动成线，线动成面，面动成体 例1、下列图形绕虚线旋转一周，例2、一个棱锥有7个面，这是 __________ 棱锥，有 _________ 个侧面。

例3、棱柱的 ____________ 长相等，上下底面是 _____________ 的多边形，侧面是 例4、下图3.1-8是图（1）的正方体切去一块，得到图（2）~（ 5）形成一个几何体，在对应横线上，写出几何体的名称。

例2、点动成线，线动成面，面动成体，请举实例说明。

3、知识点3 :棱锥、棱柱的棱、侧棱、顶点、底面的概念与统计 1）、n 棱锥有 ________ 条棱， ________ 个顶点， ________ 个面。

n 棱柱有 顶点， ________ 个面。

例1、4棱锥有 _________ 条棱， 顶点， ________ 个面。

个顶点, 个面。

5棱柱有 条棱, 条棱,的几何体,它们各有多少个面？多少条棱？多少个顶点？4、知识点4:欧拉公式的内容例1、将正方体的面数记为f，边数记为e，顶点数记为V，贝U f+v-e= （）A 1B 、2C 、3D 、4例2、有一个几何体，有9个面，16条棱，那么它有__________________ 个顶点。

5、知识点5:图形的变化方式：平移、旋转、翻折下列图形都是由半圆经过变化而得到的，请说出它们最简单的变化过程。

例2、如图，先将图（1）中的图形平移到图（2）的方格中，然后绕右下角的顶点旋转180 °到图（3）的方格中，再翻折到图（4）的方格中。

例3、小明用如下左图的胶滚沿从左到右的方向将图案滚涂到墙上, 案中符合胶滚的图案的是右边所给的四个图（）二、练习面。

第5课时走进图形世界单元复习【知识整理】1．图形由_______、_______、_______组成，点动成_______，线动成_______，面动成_______．2．图形经过平移、______、______后得到的新图形与原图形在大小、形状上都没有变化．3．一个立体图形展开后得到_______图形，某些平面图形折叠后可得到_______图形．在展开与_______的过程中，要注意棱与折痕的关系．4．立体图形的三视图指：_______、_______和_______，通过三视图可以把一个立体图形的各个部位的精确尺寸表示出来；由三视图（平面图形）也能“还原”_______图形．5．矩形绕其一边旋转一周形成的几何体叫_______，直角三角形绕其中一条直角边旋转一周形成的几何体叫_______．【单元训练】1．圆绕着它的一条直径旋转一周所得到的几何体是_______．2．长方体由_______个面围成，圆柱由_______个面围成，圆锥由_______个面围成．3．主视图、左视图和俯视图都是正方形的几何体是_______，几何体中主视图是圆，左视图和俯视图都是长方形，该几何体是_______．4．五棱柱有_______个顶点，_______条棱，_______个面．5．点动成_______，线动成_______．6．举出2个主视图是圆的不同物体的例子：_______．7．小明用如图所示的胶滚沿从左到右的方向将图案滚涂到墙上，下边所给的四个图案中符合胶滚的图案的是( )8．两个完全相同的正方体，将一面完全重合，构成的几何体的面数有( ) A．12个B．11个C．10个D．6个9．用6根长度相等的火柴棒搭等边三角形，最多可搭成( )A．2个B．3个C．4个D．5个10．将一个正方体沿着某些棱剪开，展开成一个平面图形，至少需要剪的棱有( ) A．5条B．6条C．7条D．8条11．如图所示的陀螺是由下面哪两个几何体组合而成的( )A．长方体和圆锥B．长方体和三角形C．圆和三角形D．圆柱和圆锥12．用一个平面去截一个正方体截面的形状不可能是( )A．四边形B．五边形C．六边形D．七边形13．下列四个几何体中，主视图与俯视图不同的共有( )A．1个B．2个C．3个D．4个14．如图是一个由多个相同的小正方体堆积而成的几何体的俯视图，图中所示数字为该位置小正方体的个数，则这个几何体的左视图是( )15．画出下列几何体的三视图．16．如图是一个正方体纸盒的展开图，请把8、－3、－15分别填入余下的3个正方形中，使得按虚线折成正方体后，相对面上的两个数互为相反数．17．将如图所示方格中的阴影部分的图形绕着点O逆时针旋转90°，画出旋转后的图形．18．在平整的地面上，有若干个完全相同的棱长为10 cm的小正方体堆成一个几何体，如图所示．(1)这个几何体由_______个小正方体组成，请画出这个几何体的三视图．(2)如果在这个几何体的表面喷上黄色的漆，则在所有的小正方体中，有_______个正方体只有一个面是黄色，有_______个正方体只有两个面是黄色，有_______个正方体只有三个面是黄色．(3)若现在你手边还有一些相同的小正方体，如果保持俯视图和左视图不变，最多可以再添加几个小正方体？这时如果要重新给这个几何体表面喷上红漆，需要喷漆的面积比原几何体增加还是减少了？增加或减少了多少平方厘米？19．小明把棱长为4的正方体分割成了29个棱长为整数的小正方体，则其中棱长为1的小正方体的个数是( )A．22 B．23 C．24 D．2520．墙角处有若干个大小相同的小正方体堆成如图所示的立体图形，如果你打算搬走其中部分小正方体（不考虑操作技术的限制），但希望搬完后从正面、上面、右面用平行光线照射时，在墙面及地面上的影子不变，那么你最多可以搬走多少个小正方体？参考答案1．球 2.6 3 23．正方体圆柱 4. 10 157 5．线面6．答案不唯一，如圆柱，球7．C8.D9.C10.C11.D12.D13.B14.D 15~17．略18．(1)10 图略(2)1 2 3 (3)4个增加了400 cm219．C20．27个。

第5章走进图形世界复习一、【知识梳理】【训练巩固】（一）、填空题：1、圆围绕着它的一条直径旋转一周所得到的几何图形是。

2、当下面这个图案被折成一个正方体时，数字1对面的数字是？3、长方体由个面围成，圆柱由个面围成，圆锥由个面围成。

4、五棱柱有个顶点，条棱，个面。

5、点动成，线动成。

6、主视图、左视图和俯视图都是正方形的几何体是。

7、把四个棱长为1cm的正方体按图3.5-1所示堆放于地面，则其表面积为 cm2。

8、如图3.5-2的三视图所画的几何体是。

9、几何体中正视图是圆，左视图和俯视图都是长方形，该几何体是。

10、在平整的地面上，有若干个完全相同的棱长为10cm的小正方体堆成一个几何体，如图所示。

（1）这个几何体由个小正方体组成，请画出这个几何体的三视图。

主视图左视图俯视图（2）如果在这个几何体的表面喷上黄色的漆，则在所有的小正方体中，有个正方体只有一个面是黄色，有个正方体只有两个面是黄色，有个正方体只有三个面是黄色。

二、选择题：11、两个完全相同的正方体，将一面完全重合，构成的几何体面数有（）A、12个B、11个C、10个D、6个12、下列几何体中，不属于多面体的是（）A、正方体B、三棱柱C、长方体D、圆锥体13、用六根长度相等的火柴棒搭等边三角形，最多搭成个。

（）A、2B、3C、4D、514、正方体的平面展开图可以是下列图形中的( )15、将一个正方体沿着某些棱剪开，展成一个平面图形，至少需要剪的棱的条数是（）A、5条B、6条C、7条D、8条16、如图3.5-4的陀螺是由下面哪两个几何体组合而成的（）A、长方体和圆锥B、长方体和三角形C、圆和三角形D、圆柱和圆锥17、用一个平面去截一个正方体截面的形状不可能是（）A、四边形B、五边形C、六边形D、七边形18、由6个小正方体组成的图形，它的主视图和俯视图如图所示，请画出它的左视图，与同学交流你画出的图形。

再搭出这个立体图形并观察验证一下。

2023-2024学年苏科版数学七年级上册同步专题热点难点专项练习专题5.4 走进图形世界（章节复习+能力强化卷）知识点01：立体图形1．定义：图形的各部分不都在同一平面内，这样的图形就是立体图形，如长方体、圆柱、圆锥、球等．棱柱、棱锥也是常见的立体图形．知识要点：常见的立体图形有两种分类方法：2．棱柱的相关概念：在棱柱中，相邻两个面的交线叫做棱，相邻两个侧面的交线叫做侧棱．通常根据底面图形的边数将棱柱分为三棱柱、四棱柱、五棱柱、六棱柱……它们底面图形的形状分别为三角形、四边形、五边形、六边形……（如下图）知识要点：（1）棱柱所有侧棱长都相等．棱柱的上、下底面的形状相同，侧面的形状都是平行四边形．（2）长方体、正方体都是四棱柱．（3）棱柱可分为直棱柱和斜棱柱．直棱柱的侧面是长方形，斜棱柱的侧面是平行四边形．3．点、线、面、体：长方体、正方体、圆柱、圆锥、球、棱柱、棱锥等都是几何体,几何体也简称体；包围着体的是面,面有平的面和曲的面两种；面和面相交的地方形成线，线也分为直线和曲线两种；线和线相交的地方形成点．从上面的描述中我们可以看出点、线、面、体之间的关系．此外，从运动的观点看：点动成线，线动成面，面动成体．知识点02：展开与折叠有些立体图形是由一些平面图形围成，将它们的表面适当剪开，可以展开成平面图形，这样的平面图形称为相应立体图形的展开图．知识要点：(1)不是所有的立体图形都可以展成平面图形．例如，球便不能展成平面图形．(2)不同的立体图形可展成不同的平面图形；同一个立体图形，沿不同的棱剪开，也可得到不同的平面图．知识点03：截一个几何体用一个平面去截一个几何体，截出的面叫做截面．截面的形状可能是三角形、四边形、五边形、六边形或圆等等．知识点04：从三个方向看物体的形状一般是从以下三个方向：(1)从正面看；(2)从左面看；(3)从上面看．（如下图）一、选择题（每题2分，共20分）1．（本题2分）（2020秋·江苏南京·七年级南师附中宿迁分校校考期末）如图是一个小正方体的展开图，把展开图折叠成小正方体后，与“数”这个汉字相对的面上的汉字是（）A．我B．很C．喜D．欢2．（本题2分）（2021春·江苏南京·七年级南师附中树人学校校考阶段练习）如图是由5个立方块搭成的几何体的俯视图，小正方形中的数字表示该位置上的小立方块的个数，则这个几何体的主视图是（）A．B．C．D．3．（本题2分）（2020秋·江苏盐城·七年级统考期末）如图1是一个小正方体的侧面形展开图，小正方体从图2中右边所示的位置依次翻到第1格，第2格，第3格，这时小正方体朝上一面的字是（ ）A ．中B ．国C ．江D ．苏4．（本题2分）（2020秋·江苏南京·七年级统考期末）如图所示，在一个正方形盒子的六面上写有“祝”、“母”、“校”、“更”、“美”、“丽”六个汉字，其中“祝”与“更”，“母”与“美”在相对的面上，则这个盒子的展开图（不考虑文字方向） 不可能的是（ ）A ．B ．C ．D ．5．（本题2分）（2020秋·江苏徐州·七年级校考阶段练习）如图，该表面展开图按虚线折叠成正方体后，相对面上的两个数互为相反数，则()x y +的值为（ ）A ．－2B ．－3C ．2D ．16．（本题2分）（2019春·江苏无锡·七年级无锡市江南中学校考开学考试）如图是一个正四面体，现沿它的棱AB 、AC 、AD 剪开展成平面图形，则所得的展开图是（ ）A．B．C．D．7．（本题2分）（2019秋·江苏苏州·七年级统考期末）由n个相同的小正方体搭成的几何体，其主视图和俯视图如图所示，则n的最小值为（）A．10 B．11 C．12 D．138．（本题2分）（2022秋·江苏宿迁·七年级泗阳致远中学校考期末）在一个不透明的布袋中，装有一个简单几何体模型，甲乙两人在摸后各说出了它的一个特征，甲：它有曲面；乙：它有顶点。

课题：第五章走进图形世界复习俯视图左视图主视图课 题：第五章 走进图形世界复习 学案编号：7150 姓名【学习目标】从变换（展开、折叠、平移、旋转和翻折等）的角度认识几何图形，感受丰富的图形世界是由“基本图形”构成的．【学习重点】平面图形与空间图形对应关系的确定．【问题导学】问题1．观察：下图中的几何体是由若干个完全相同的小正方体搭成的．(1)画出几何体的主视图，左视图，俯视图？(2)能移走一个小正方体使它的三个视图都不变吗？问题2．如图是一个由若干个相同的小正方体搭成的几何体的三种视图，组成这个几何体的小正方体的个数为（ ）A ．5个B ．6个C ．7个D ．8个问题3．若在上述折叠的正方体表面上画如图所示的线段，请你在展开图上标出对应的其它两条线段．点数为 ． 5．一个几何体，是由许多规格相同的小正方体堆积而成的，其正视图、左视图如图所示，要摆成 这样的图形，至少需用 块正方体，最多需 用正方体．6．一个立体图形的三视图形如图所示，则该立体图形是（ ） 正视图 左视图俯视图A ．圆锥B ．球C ．圆柱D ．圆7． 一个四棱柱被一刀切去一部分，剩下的部分可能是( )A ．四棱柱B ．三棱柱C ．五棱柱 D ．以上都有可能8．如图所示是一多面体的展开图形，每个面都标有字母，请根据要求回答提问：（1）如果面A 在多面体的底部，那么面 在上面．（2）如果面F 在前面，从左面看是面B ，则正视图 左视图 第5题图面在上面．（3）从右面看是面C，面D在后面，面在上面．。