第7章 轴测投影图
- 格式:pdf
- 大小:591.24 KB
- 文档页数:30

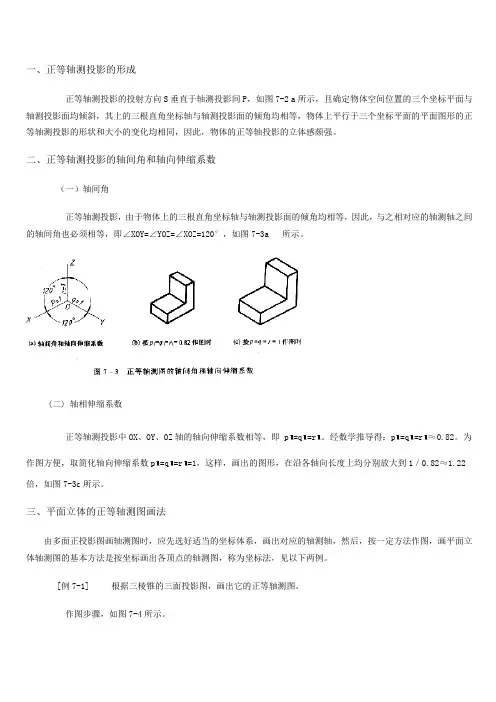
一、正等轴测投影的形成正等轴测投影的投射方向S垂直于轴测投影间P,如图7-2 a所示,且确定物体空间位置的三个坐标平面与轴测投影面均倾斜,其上的三根直角坐标轴与轴测投影面的倾角均相等,物体上平行于三个坐标平面的平面图形的正等轴测投影的形状和大小的变化均相同,因此,物体的正等轴投影的立体感颇强。
二、正等轴测投影的轴间角和轴向伸缩系数(一)轴间角正等轴测投影,由于物体上的三根直角坐标轴与轴测投影面的倾角均相等,因此,与之相对应的轴测轴之间的轴间角也必须相等,即∠XOY=∠YOZ=∠XOZ=120°,如图7-3a 所示。
(二) 轴相伸缩系数正等轴测投影中OX、OY、OZ轴的轴向伸缩系数相等,即 p=q=r。
经数学推导得:p=q=r≈0.82。
为作图方便,取简化轴向伸缩系数p=q=r=1,这样,画出的图形,在沿各轴向长度上均分别放大到1/0.82≈1.22倍,如图7-3c所示。
三、平面立体的正等轴测图画法由多面正投影图画轴测图时,应先选好适当的坐标体系,画出对应的轴测轴,然后,按一定方法作图,画平面立体轴测图的基本方法是按坐标画出各顶点的轴测图,称为坐标法,见以下两例。
[例7-1] 根据三棱锥的三面投影图,画出它的正等轴测图。
作图步骤,如图7-4所示。
[例7-2] 根据六棱柱的三面投影图,画出它的正等轴测图。
作图步骤,如图7-5所示。
本题关键在于选定坐标轴和坐标圆点,如先确定顶面各点的坐标,可避免画不必要的作图线。
四、曲面立体的正等轴测图的画法(一)坐标平面(或其平面)上的圆的正等轴测投影坐标平面(或其平行面)上圆的正等轴测投影为椭圆。
立方体平行于坐标平面的各表面上的内切圆的正等轴测投影,如图7-6所示。
从图7-6中可以看出:(1)分别平行于坐标平面的圆的正等轴测投影均为形状和大小完全相同的椭圆,但其长轴和短轴方向各不相同。
(2)各椭圆的长轴方向垂直于不属于轴测投影(即轴测轴),且在菱形(圆的外切正方形的轴测投影)的长对角线上;短轴方向平行于不属于此坐标平面的那根坐标轴的轴测投影(即轴测轴),且在菱形的短对角线上。





轴测投影图本章简介:本章主要介绍轴侧投影图。
轴测图是一种单面投影图,在一个投影面上能同时反映出物体三个坐标面的形状,并接近于人们的视觉习惯,形象、逼真,富有立体感.但是轴测图一般不能反映出物体各表面的实形,因而度量性差,同时作图较复杂.因此,在工程上常把轴测图作为辅助图样,来说明机器的结构、安装、使用等情况,在设计中,用轴测图帮助构思、想象物体的形状,以弥补正投影图的不足。
本章要求学生了解轴测投影的基本知识,掌握正等侧、斜轴测投影图的画法,具体内容包括轴测投影图的基本知识、正等轴测图、斜轴测图等。
学习重点1. 正等侧、斜轴测的轴间角和轴向伸缩系数2. 正等侧、斜轴测投影图的画法6.1 轴测投影的基本知识图6-1 (a)和图6-1 (b)分别示出同一形体的三面投影图和轴测投影图。
比较这两种图可以看出:三面正投影图既能完整地反映形体的真实形状,又便于标注尺寸,所以在工程中被广泛采用。
但这种图缺乏立体感,需要受过专门训练者才能看懂,而且读图时必须把几个投影图联系起来,才能想象出形体的全貌。
轴测投影图是在一个投影上同时反映形体的长、宽、高三个向度,立体感较强,但度量性较差,作图也较繁琐。
在工程中常采用轴测投影图来弥补多面正投影图直观性差的缺点,故轴测投影图是一种辅助图样。
(a)(b)图6-1 正投影图与轴测投影图(a)三面投影图(b)轴测投影6.1.1 轴测投影图的形成图6-2示出轴测投影图的形成过程。
将形体连同确定其空间位置的直角坐标系,用平行投影法,沿S方向投射到选定的一个投影面P(或Q)上,所得到的投影称为轴测投影。
用这种方法画出的图,称为轴测投影图,简称轴测图。
(a)(b)图6-2 轴测投影图的形成(a)正轴测投影图的形成(b)斜轴测投影图的形成6.1.2 轴间角和轴向伸缩系数如图6-3所示。
当物体连同坐标轴一起投射到轴测投影面(P)上时,坐标轴OX、OY、OZ的投影O1X1、O1Y1、O1Z1称为轴测投影轴。


轴测投影图轴测投影图概述正等轴测图正二等轴测图斜二等轴测图水平斜轴测图VV轴测投影图概述——轴测图的形成轴测图是用平行投影法在一个投影面上同时反映物体三维形状的投影图,它直观性较强,但作图复杂,且不能准确表达物体的原形和大小,多作为辅助图样使用。
轴测图的形成方法有两种:正轴测图斜轴测图Z 1X 1O 1Z 1X 1O 1Z 1O 1X 1Y 1Z 1X 1O 1Y 1Y XZ OXYZ OYXZO轴测投影图概述——轴测图的基本要素r = O 1Z 1/O Z X 1Y 1Z 1O 11、轴测轴空间物体的三个坐标轴OX 、OY 和OZ 在轴测投影面上的投影O 1X 1、O 1Y 1和O 1Z 1称为轴测轴。
2、轴间角在轴测投影面上,每两个轴测轴之间的夹角称为轴间角。
3、轴向变形系数轴测轴上的线段与空间物体相应坐标轴上的对应线段长度之比称为轴向变形系数。
轴间角和轴向变形系数是轴测图中决定物体空间位置或投影方向的作图依据。
——p = r ≠q——p = r ≠q轴测投影图概述——轴测图的分类用正投影法得到的轴测图正轴测图斜轴测图轴测图正等轴测图正二等轴测图正三轴测图斜等轴测图斜二等轴测图斜三轴测图用斜投影法得到的轴测图——p = q = r——p ≠q ≠r——p = q ≠r——q = r ≠p——p = q = r——p ≠q ≠r——p = q ≠r——q = r ≠p轴测投影图概述——轴测图的投影特点VVZ 1X 1O 1Z 1X 1O 1Z 1O 1X 1Y 1Z 1X 1O 1Y 1Y XZ OXYZ OYXZO由于轴测图采用的仍是平行投影,因此它具有平行投影的一般性质,即在原物体与轴测投影间保持以下关系:●空间平行且等长的两直线,其轴测投影也必平行且等长。
●物体上平行于物体空间坐标轴的直线,其轴测投影必平行于相应的轴测轴。
正等轴测图r = 1——正等轴测图的基本要素X 1Y 1Z 1O 1120°120°120°如图所示,若使正等轴测图的三个轴向变形系数均相等,需要保证空间物体的三个坐标轴与轴测投影面的倾角相等,即为35º16'。