07第7章轴测投影

11 轴测投影图一、轴测投影的基本知识二、正等测的画法三、斜等测和斜二测的画法四、轴测投影的选择一、轴测投影的基本知识1、轴测投影的形成和作用2、轴间角和轴向伸缩系数3、轴测投影的分类及应用1、轴测投影的形成和作用轴测投影——将物体连同确定物体的坐标轴，向一个与确定该物体的三个坐标面倾斜的投影面投影，所得的平行投影即为轴测投影。

该投影面称为轴测投影面。

在工程中，轴测投影图一般作为工程辅助图样。

轴测轴——三个坐标轴X 1、Y 1、Z 1的轴测投影X 、Y 、Z 。

轴间角——轴测轴之间的夹角，∠XOY 、∠YOZ 、∠ZOX 轴倾角——轴测轴X 、Y 与水平线间的夹角。

轴向伸缩系数——轴测轴上的单位长度与对应坐标轴上的单位长度之比。

X 轴轴向伸缩系数:p=OA/O 1A 1Y 轴轴向伸缩系数:q=OB/O 1B 1Z轴轴向伸缩系数：r=OC/O CPOCA B YZX推论: 与坐标轴平行的棱线，其轴测投影平行于对应的轴测轴，其轴向伸缩系数Z1Y1 X1O1B1A1C12、轴间角和轴向伸缩系数轴测投影正轴测投影斜轴测投影正等测正二测正三测p = q = rp = 2q = rp ≠ q ≠ r 斜等测斜三测p = q = rp = 2q = r 斜二测p ≠ q ≠ r3、轴测投影的分类及应用正等测的轴测轴和轴向伸缩系数YZXOr = 0.82q = 0.82p = 0.8230°30°120°120°120°YZXOr = 1q = 1p = 130°30°120°120°120°简化后轴向伸缩系数二、正等测的画法⑴四心法X 1Y 1A 1B 1C 1D 11234ACDBXYXYZ 111O 1O 212341、平行于坐标面的圆的正等测画法⑵八点法X 1Z 1A 1B 1C 1D 11234efgh45°XZCBAD1234E FGH45°ZXY1112、物体的正等测画法⑴绘制物体轴测投影的基本方法：•坐标法：根据物体上各点坐标，作出它们的轴测投影后连线。

机械制图课件-轴测投影图知识1. 轴测投影图的概念轴测投影图是一种用于展示三维物体形状和结构的图形表达方法。

它可以将三维物体的各个面投影到一个二维平面上，以便更清晰地显示物体的细节和几何关系。

2. 轴测投影图的种类常见的轴测投影图有等轴测、斜轴测和正轴测三种。

其中：•等轴测投影图：物体的三个主轴（长轴、宽轴、高轴）之间的夹角相等，投影图比例为1:1。

•斜轴测投影图：物体的三个主轴之间夹角不相等，通常以45度或30度为倾斜角度。

•正轴测投影图：既可以是等轴测投影图，也可以是斜轴测投影图的投影比例不为1:1的情况。

3. 轴测投影图的主要特点轴测投影图具有以下主要特点：•保持物体的形状：轴测投影图可以保持物体的真实形状，不会发生形变。

•显示物体的所有面：轴测投影图可以显示物体的前、后、上、下、左、右等各个面，使得观察者可以全方位地观察物体的外观。

•清晰明了：轴测投影图的投影线条清晰明了，不会出现视觉上的混淆。

•便于测量和设计：通过轴测投影图可以方便地进行测量和设计，尺寸和比例可以轻松确定。

4. 轴测投影图的制作步骤制作轴测投影图的一般步骤如下所示：1.确定物体的主轴方向，即长轴、宽轴和高轴。

这需要根据物体的形状和结构来决定。

2.根据主轴方向确定投影面，即确定物体的前、后、上、下、左、右等各个面。

确定投影面后，可以根据需要选择一个合适的投影比例。

3.根据物体的真实尺寸，将物体的各个面投影到投影面上。

需要注意的是，投影过程中需要保持直线、点、面等几何元素的相对位置和关系。

4.在投影面上绘制出投影图，使用合适的标线和符号来表示不同的元素和特征。

5. 轴测投影图的应用领域轴测投影图在机械制图中有广泛的应用，尤其适用于以下领域：•机械设计：轴测投影图可以帮助工程师实现对机械零件和装配件的设计和效果展示。

•工艺制作：轴测投影图可以辅助制造工艺的规划和排布，提高生产效率。

•建筑设计：轴测投影图能够帮助建筑师表达建筑物的立面、平面和空间结构，方便设计和施工。

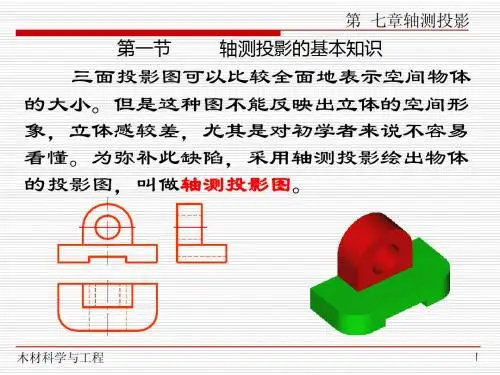
07第七章轴测投影第一节轴测投影的基本知识第二节正等轴测图的画法第三节正二测图的画法第四节斜二测图的画法第五节轴测剖视图的画法第六节轴测图上交线的画法多面正投影图直观性差，度量性好轴测投影图7-1第一节轴测投影的基本知识每面投影仅表达两个方向一、轴测投影图的形成正轴测图：S⊥P斜轴测图：S∠P•1.轴测投影面：P •2.轴测轴：X I，Y I，Z I •3.轴间角φZ1X1Y1坐标轴X,Y,Z轴测轴φ1φ2φ3长度有变化二、轴测投影的基本性质1.平行性：平行线段的投影仍平行。

2.平行线段变形系数相等。

3.与轴测轴平行的线段，其变形系数等于轴向变形系数。

4.与轴测投影面平行的线段（或平面图形）反应实长（或实形）。

Z 1X 1Y 1一、基本知识1、轴间角：三个均为120°2、轴向变形系数：p ＝q ＝r ≈0.823、简化轴向变形系数：p ＝q ＝r ≈1 (图的轴向尺寸放大1.22倍——1/0.82）120°30°轴测轴画法7-2-0第二节正等轴测图的画法S 1二、轴测图的基本画法——坐标取点法A(x A ,0,0), B(0,0,0), C(x C ,y C ,0) , S(x S ,y S ,z S )B 1A 1C 1bsS一般不画虚线坐标系的建立：要有利于作图，有利于表达出结构特点。

yxoz′x′o′1345621′4′3′5′2′6′a′z′x′o′1345621′3′5′2′6′a′x 1y 1o 1ab4′求点Ⅰ(x,0,0)按对称性求点ⅢⅣⅤⅥ描深图线求点Ⅱ(x,y,0)三、平行于坐标面的圆的正等轴测图P＝q＝r≈0.82简化系数：P＝q＝r≈1短轴方向？O 3O 4O 1O 2水平圆正等轴测图的画法——四心法近似画法y xX 1Y 1Z 1dcba A 1B 1C 1D 1切点切点四心水平圆正等轴测图的画法——辅助圆求八点X 1Y 1Z 1y x d c b aA 1B 1C 1D 1O 3O 4O 1O 2四、圆柱正等轴测图的画法一将圆弧中心下移—移心法圆柱正等轴测图的画法二短轴方向：圆柱轴线方向圆柱正等轴测图的画法三三种方向正等轴测圆柱的比较短轴方向：圆柱轴线方向五、圆台正等轴测图的画法短轴方向：圆台轴线方向7-六、圆角正等轴测图的画法x 1y 1z 1ⅢⅣⅡⅠ画1/4圆柱画1/4圆柱7-圆角正等轴测图的画法切点切点向下平移七、组合体画法例题1.Z1X1Y1平行性求交线O’O例题2.切点切点X 1Z 1Y 1例题2.复习、预习、作业指导JC P130 ~ P137JC P140~143XT P377-3-0第三节正二测图的画法平行于坐标面的圆的正二测图简化轴向变形系数：p ＝r ＝1 q ≈0.5 (图的轴向尺寸放大）轴向变形系数：p ＝r＝0.94 q ≈0.47椭圆画法正二测图作图示例在轴测图上尺寸的标注：按轴向画尺寸线。

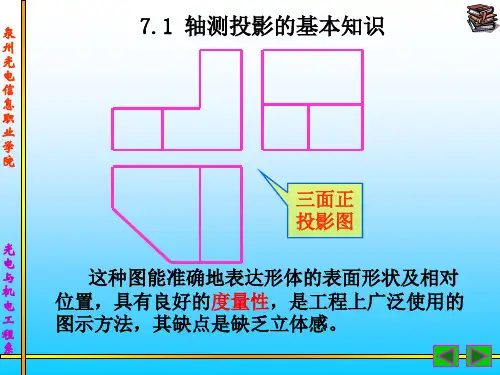
6.1.1 轴测投影图的形成如图6-1所示，在作形体投影图时如果选取适当的投影方向将物体连同确定物体长、宽、高三个尺度的直角坐标轴，用平行投影的方法一起投影到一个投影面<轴测投影面）上所得到的投影，称为轴测投影。

应用轴测投影的方法绘制的投影图叫做轴测图。

<a）正轴测投影图的形成<b）斜轴测投影图的形成图6-1轴测投影图的形成6.1.2轴间角和轴向伸缩系数如图6-1所示。

当物体连同坐标轴一起投射到轴测投影面<P或Q）上时，坐标轴OX、OY、OZ的投影O1X1、O1Y1、O1Z1称为轴测投影轴。

轴测轴之间的夹角∠X1O1Y1、∠Y1O1Z1、∠X1O1Z1称为轴间角。

轴测轴上某线段长度与它的实长之比，称为轴向伸缩系数。

=p ，称X轴向伸缩系数；=q ，称Y轴向伸缩系数；=r ，称Z轴向伸缩系数。

6.1.3轴测投影的分类 6.1.3.1 根据投射线和轴测投影面相对位置的不同，轴测投影可分为两种：<1）正轴测投影投射线S 垂直于轴测投影面P (如图6-1<a）所示>。

<2）斜轴测投影投射线S倾斜于轴测投影面Q (如图6-1<b）所示>。

6.1.3.2 根据轴向变形系数的不同，轴测投影又可分为三种：<1）正<或斜）等轴测投影p=q=r；<2）正<或斜）二等轴测投影p＝q≠r或p＝r≠q或p≠q＝r；<3）正<或斜）三测投影p≠q≠r。

6.1.4轴测投影的性质轴测投影是在单一投影面上获得的平行投影，所以，它具有平行投影的特性。

<1）空间平行的线段，其轴测投影仍相互平行。

因此，形体上平行于某坐标轴的线段，其轴测投影也平行于相应的轴测轴。

<2）空间平行二线段长度之比，等于相应得轴测投影长度之比。

因此，平行于坐标轴的线段的轴测投影与线段实长之比，等于相应的轴向伸缩系数。

b5E2RGbCAP6.2 正等轴测图 6.2.1轴间角和轴向伸缩系数正等轴测图<简称正等测），即它们的轴向伸缩系数p=q=r。