当前位置：文档之家 › 平面任意力系平衡

平面任意力系平衡

  • 格式：pptx
  • 大小：131.09 KB
  • 文档页数：7

下载文档原格式

  / 7

合集下载

理论力学2.2、平面任意力系的合成与平衡

理论力学2.2、平面任意力系的合成与平衡
m F1 OA F2 OB F1 ( OB OA) F1 AB
m F1 OA F2 OB F1 ( OA OB ) F1 AB
3
力 线 作用在刚体上的力可以离开其作用线而平 平 行移动到刚体上任意位置处,但必须对刚体 移 附加一个力偶,附加力偶的力偶矩等于原力 定 对平移后所得新力作用点的力矩。 理
求细绳的拉力和A、B两处的支持力。
解、研究对象：AB，受力 如图所示，则有：


Fix Fiy mD
0 0
(Fi )

0

FB FD G FA c
FA
os
sin 0
FB

BD

G

AB 2
0 sin
FA

AD

0
FA 115.5(N) FB 72.2(N ) FD 129.9(N) 12
例2.2-6、匀质细杆AB长度为L，重量为mg，静 止在半径为r的光滑半圆槽内（图2.2-17），
L=3r；求AB杆与水平线之间的夹角
解、研究对象:AB杆,受力如 图所示,则有:
Fix 0 Fiy 0 mO (Fi ) 0

FB FB
cos(2 ) FD sin sin(2 ) FD cos
d mO 2402 3.39(m) FR 709 .5
xE
d
sin

3.39 sin 70.8
3.59(m)
y yE tan 70.8 (x xE ) y 2.87x 10.31 0
10
课堂练习题(图示)：

平面任意力系平衡方程讲解课件

平面任意力系平衡方程讲解课件

01
02
03
04
仅适用于小变形的情况
对于大变形或复杂的结构，需 要使用更高级的力学理论
仅适用于线性弹性材料
对于非线性弹性材料或塑性材 料，需要使用更高级的材料模
型
04
平面任意力系平衡方 程的优化与改进
优化求解算法
线性化求解
将平衡方程转化为线性方程，降 低求解难度，提高求解速度。
迭代法优化
采用更高效的迭代算法，如牛顿法 、拟牛顿法等，加快收敛速度。
03
平面任意力系平衡方 程的适用范围
适用场景与条件
适用于平面任意力系 的平衡问题
力的作用点可以不在 物体的重心上
物体处于平衡状态， 即没有加速度或速度
不适用场景与原因
不适用于空间力系的平衡问题
不适用于具有加速度或速度的 物体
力的作用点不在物体的重心上 时，需要考虑科氏力等因素
限制因素与局限性
平衡状态
物体在受到一组的力作用后，如果处 于静止或匀速直线运动状态，则称该 物体处于平衡状态。
平衡方程
对于平面任意力系，其平衡方程为合 力为零，即合力在x轴和y轴上的投影 分别为零。
02
平面任意力系的平衡 方程
平衡方程的推导
1 2 3
静力平衡
在无外力作用下，物体处于静止状态，此时物体 内部各部分之间无相对运动趋势，处于平衡状态 。
并行计算
利用多核CPU或分布式计算资源， 实现并行计算，大幅缩短求解时间 。
提高计算精度
精细化建模
采用更高精度的物理模型，提高 方程的准确性和精度。
高阶有限元方法
采用高阶有限元方法，降低误差 ，提高计算精度。
自适应步长控制
根据误差大小自动调整步长，确 保计算的稳定性和精度。

基础篇 单元三 平面力系的平衡

基础篇 单元三 平面力系的平衡
静不定问题并不是绝对不能解决的问题，只是仅利用静力 学的方法不能解决。
当物系平衡时，系统内的每一部分都是平衡的。既可以选 择整个物系为研究对象，也可以选择其中的某几个或某一个物 体作为研究对象。
单元三 平面力系的平衡
课题三 物体系统的平衡
对于一般的静定物系平衡问题，应首先画出整体、局部或单 个物体的受力图，再从有已知力且未知量数少于或等于独立平衡 方程数的物体着手分析，便可解除全部未知量。若物系内分离体 均不符合可解条件，必须寻找有局部可解条件的分离体。
课题一 平面任意力系的平衡
单元三 平面力系的平衡
课题一 平面任意力系的平衡
由平衡方程可知，平面任意力系平衡的解析条件为：力系 中各力在两个任选的坐标轴上投影的代数和等于零，各力对力 系作用面内任意一点之矩的代数和等于零。除基本形式之外， 平面任意力平衡方程还可表示为二力矩形式。

M M
座的约束力。
解 (1)取齿轮轴为研究对象，画其受力图，如图3-2b。
(2)建立直角坐标系Axy，如图3-2b所示，列平衡方程求解
单元三 平面力系的平衡
课题一 平面任意力系的平衡
Fx 0 F FBx 0
解得 FBx F
M A(F) 0 FA 3a F 2a 2Fa Fa 0 解得 FA F
3 kN 11.4kN 2
将FT代入式(b)得 FAy G1 G2 FT sin 2.1kN
本题也可用二力矩式求解。
单元三 平面力系的平衡
课题一 平面任意力系的平衡
例3-3 减速器中的齿轮轴Ｂ端可分别简化为固定铰支座，
Ａ端可简化为可定铰支座，如图3-2a所示。已知Ｆ、a，求两支
解 取工件为研究对象。工件在水平面受三个力偶和两个螺 栓的水平约束力的作用，三个力偶合成后仍为一力偶，若工件 平衡，必有一约束力偶与它相平衡，因此螺栓A和B的水平力 FNA和FNB必组成一力偶，方向如图3-5b所示，且FNA=FNB 。列 平衡方程

平面任意力系的平衡资料

平面任意力系的平衡资料

' FDx FE cos 45 2 F
MB o
' FDx a F 2a 0
得
' FDx 2F
对ADB杆受力图
MA 0
FBx 2a FDx a 0
得
FBx F
例311 如图所示，静定多跨梁由梁AB和梁BC用中间铰B连 接而成。已知P＝20kN，q＝5kN/m，α＝450，求支座A、C处 的约束反力和中间铰B处两梁之间的相互作用力。
O1 B O2 A
三矩式平衡方程为：
相比较二矩式最简单
M M M
O1 O2 C
0 :N B 2a W cos a W sin b 0 0 : N A 2a W cos a W sin b 0 0 : T b N Aa N B a 0
二矩式平衡方程为：
X 0 : T W sin 0 M 0 :N 2a W cos a W sin b 0 M 0 : N 2a W cos a W sin b 0
O1 B O2 A
解得：
T W sin 5kN W cos a W sin b NA 3.33kN 2a W cos a W sin b NB 5.33kN 2a
解得
FAy q 2a P FB 0
P 3 FAy qa 4 2
已知：P 100kN, M 20kN m,
q 20 kN
求： 固定端A处约束力。 解：取T型刚架，画受力图。
1 其中 F1 q 3l 30kN 2
m
,

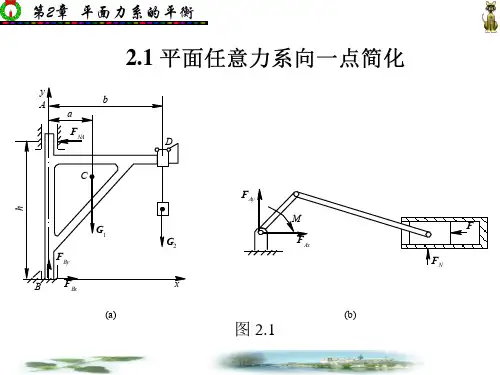
平面任意力系的平衡方程及应用

平面任意力系的平衡方程及应用

FCDl
s in

G1
l 2

G2a

0
(a)
Fx 0 FAx FCD cos 0
(b)
Fy 0 FAy G1 G2 FCD sin 0
(c)
第2章 平面力系的平衡
C
A

D
C
l
2a
G 1
l
G2 (a)
y FAy A
FAx
图2.5
FCD
B x
G1
G2
(b)
FR'
Fx 2 Fy 2 0, MO MO (Fi ) 0
第2章 平面力系的平衡
由此可得平面任意力系的平衡方程为
Fx 0
Fy 0
Байду номын сангаас

MO (F ) 0
式（2.6）是平面任意力系平衡方程的基本形式，也称为一 力矩式方程。它说明平面任意力系平衡的解析条件是: 力系中各 力在平面内任选两个坐标轴上的投影的代数和分别为零，以及 各力对平面内任意一点之矩的代数和也等于零。这三个方程是 各自独立的三个平衡方程，只能求解三个未知量。
解（1） 选圆球为研究对象，取分离体画受力图。 主动力: 重力G。 约束反力: 绳子AB的拉力FT、斜面对球的约束力FN。 受力图如图2.6（b）所示。
第2章 平面力系的平衡
（2） 建立直角坐标系Oxy
∑Fx=0
FT-Gsin30°=0
FT=50N( ∑Fy=0
FN-G cos30°=0
FN=86.6N
解 （1）以横梁AB为研究对象，取分离体画受力图。
作用在横梁上的主动力: 在横梁中点的自重G1、起吊重量 G2。作用在横梁上的约束反力: 拉杆CD的拉力FCD、铰链A点的 约束反力FAx、FAy，如图2.5（b）所示。

工程力学-平面任意力系平衡方程

工程力学-平面任意力系平衡方程
大小与简化中心的选择无关。
4）FR=0 Ｍ0=0 力系处于平衡状态。
例3-1 图示物体平面A、B、C三点构成一等边三角形，三点分别作
用F力，试简化该力系。
解：1.求力系的主矢
F x F F cos60o F cos60o 0
Fy 0 F sin 60o F sin 60o 0
y
C
F M0 F
上作用F力，集中力偶M0=Fa，=45°，试求杆件AB的约束力。
A
M0=Fa
C
B
F
解：1.取AB杆为研究对象画受力图
2.列平衡方程求约束力
Da a
FAx
A
M0=Fa
C
FAy FC
B F
aa
M A (F ) 0 : FC sin 45 a F 2a M 0 0
FC
2Fa a
Fa 2/2
MC (F) 0:
FAx
2
3a 3
F
a
M0
0
FAy 0 FAx 3F
C aa
一 矩
MA(F) 0: Fx 0 :
二 矩
MA(F) 0: MB(F) 0:
三 矩
MA(F) 0: MB(F) 0:
2 3a
式 Fy 0 :
式 Fx 0 :
式 M C (F8) 0 :
3
本课节小结
A F
B x
FR ( Fx )2 ( Fy )2 0
2.选A点为简化中心，求力系的主矩
M0
M A (F)
F
sin 60
AB
F
AB 2
简化结果表明该力系是一平面力偶系。
4
二、平面任意力系的平衡方程

平面任意力系的平衡方程的三种形式

平面任意力系的平衡方程的三种形式一、概述1. 平面任意力系概念的简介在物体力学中，平面任意力系是一个很重要的概念。

平面任意力系是指一个物体在平面上受到多个力的作用，这些力可以是任意的方向和大小。

平面任意力系的研究对于分析物体的平衡和运动具有重要的意义。

2. 平衡方程的定义和作用平面任意力系的平衡方程是描述物体受力平衡的数学表达式。

通过平衡方程，可以求解物体受力的情况，从而进一步分析物体的平衡状态。

二、平面任意力系的平衡方程的三种形式1. 牛顿第一定律形式牛顿第一定律可以描述为：若物体受到多个力的作用，且这些力相互平衡，那物体将保持静止或匀速直线运动。

根据这一定律，可以得出平衡方程的第一种形式。

即对于平面任意力系，受力平衡时，力在x、y方向上的合力均为0，可以用数学公式表示为：ΣFx = 0；ΣFy = 0。

式中ΣFx表示x方向上的合力，ΣFy表示y方向上的合力。

当ΣFx和ΣFy都等于0时，物体在受力平衡状态。

2. 平衡方程的角度形式平衡方程的角度形式是指从物体受力的角度出发，建立平衡方程。

在平面任意力系中，受力平衡时，物体对于一个特定点的力矩的和为0。

力矩的和可以表示为：ΣM = 0。

式中ΣM表示力矩的和。

根据力矩的定义，可以将力矩表示为力乘以力臂的乘积。

可以将平衡方程的角度形式表示为：ΣM = ΣF × d = 0。

式中d表示力臂的长度。

当ΣM等于0时，说明物体对于特定点的力矩平衡，即物体处于受力平衡状态。

3. 用平面力系的分解形式建立平衡方程在平面任意力系中，可以将作用在物体上的力进行分解，将力分解成在x、y方向上的分力和分力的合力。

根据此方法，可以建立平衡方程的分解形式：ΣFx = 0；ΣFy = 0。

这种形式的平衡方程适用于多种情况，可以将力分解成任意方向上的分力，从而更加灵活地分析物体的受力情况和平衡状态。

三、平衡方程的应用1. 建立平面任意力系的平衡方程在实际问题中，可以通过观察和分析物体受力的情况，建立平衡方程，从而求解物体受力平衡的情况。

平面任意力系 简化与平衡


P
列平衡方程 MB Fi 0,
FA b W a b Ge Pl 0
解得
FA
1 b
W
a
b
G
e
P
l
A
B
FA b FB
将其代入条件 FA ≥ 0，即得满载时平衡块的重量应满足
W ≥ 1 Ge Pl
ab
W ≤ Geb
a
W ≥ 1 Ge Pl
ab
所以，要保证起重机在空载和 满载时都不翻倒，平衡块重应 满足不等式
y FT
FAx A
D
FAy
FB
Bx
P
2m 1m
3m
4）求解未知量
解得
FAx 2.4 kN
FAy 1.2 kN
FB 0.85 kN
杆 BC 所受的力与FB是作用力与反作用力的关系，即杆 BC 所受的 力为 0.85 kN，是拉力
[例5] 横梁 AB 用三根杆支撑，受图示载荷。已知 F = 10 kN， M = 50 kN·m，若不计构件自重，试求三杆 所受的力。
2. 分布载荷的合成结果 均布载荷
q Fq ql
A
B
l/2
l
线性分布载荷
Fq ql /2
q
A
B
2l /3
l
三、平面任意力系简化结果的讨论
4）FR 0 且 MO 0
FR Fi' Fi
FR 0
F
' Rx
Fix'
Fix
F
' Ry
Fiy'
Fiy
Fix 0 Fiy 0
MO Mi MO Fi
W a
eC
G P

平面力系的平衡方程及应用

研究方法：几何法，解析法。
各力的作用线都在同一平面内且 汇交于一点的力系。
正文
力在直角坐标轴上的投影
1
Fx=F·cosa ; Fy=F·sina = F ·cosb
说明： （1）力在坐标轴上的投影为代数量； （2）力的指向与坐标轴的正向一致时，力的投影为正值，否则为负。
正文
合力投影定理
推论1：力偶对刚体的作用与力偶在其作用面内的位置无关；
推论2：只要保持力偶矩的大小和力偶的转向不变，可以同时改变力偶中力的大小和力偶臂的长短，而不改变力偶对刚体的作用。
M
M
M
力偶表示方法
正文
思考：
力偶与力的异同
共同点：单位统一，符号规定统一。 差异点：1.力矩随矩心位置不同而变化；力 偶矩对物体作用效果与矩心选取无关。 2.力偶矩可以完全描述一个力偶；力对点之矩不能完全描述一个力。
′
F
M
单 手 攻 丝
正文
平面任意力系的简化
1
平面一般力系向平面内一点简化
F3
F1
F2
O
O
O
F
R′
MO
F
1′
M1
F1 =F1
′ M1=MO(F1)
F
2′
M2
F
3′
M3
F2 =F2
′ M2=MO(F2)
F3 =F3
′ M3=MO(F3)
简化中心
O
FR=F1+F2+F3= F1+F2+F3 MO=M1+M2+M3=MO(F1)+ MO(F2) + MO(F3)
正文
平面力偶系的合成与平衡

平面任意力系的平衡

平面任意力系的平衡
1.平面任意力系的平衡条件
力系的主矢 FR 和对任一点的主矩 MO 都等于零。
平面任意力系的平衡方程：
①基本式
F=0，M 0
R
O
Fix 0 Fiy 0 M O(Fi) 0
平面汇交力系的平衡
2.平面任意力系的平衡方程其他形式
②二矩式
Fx 0 M A(F ) 0 MB (F ) 0
B A
③三矩式
F M A(F ) 0 x MB (F ) 0 MC (F ) 0
F
B
. A C
x
x轴不得垂直于AB的连线。
A、B、C三点不得共线。
上式只有三个独立方程，只能求出三个未知数。
3.平面平行力系平衡方程
力的作用线在同一平面且相互平行的力系称平面平行力系。 y 平面平行力系为平面任意力系的特殊情况，当它平衡时， F1
也应满足平面任意力系的平衡方程。
选如图的坐标，则 F =自0 然满足。于是平面平行力系 x O
的平衡方程为：
F3 Fn
F2
x
Fy 0； M O (F ) 0
平面平行力系的平衡方程也可表示为二矩式：
MA (F ) 0； MB (F ) 0 其中AB连线不能与各力的作用线平行。
平面任意力系的平衡
平面任意力系的平衡
3.联立求解
4.不翻倒的条件是：FA≥0，
所以由上式可得
G3
G2
G
A
G1 B
1.8 m
FA
2.0 m
FB
2.5 m
3.0 m
故最大起吊重量为
Gmax= 7.5 kN
平面力系的平衡问题求解步骤
1.根据问题和条件，选取研究对象。 2.分析研究对象的受力情况，画受力图。 3.根据受力类型列平衡方程。 4.求解。校核和讨论计算结果。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

FT
300
B
பைடு நூலகம்
DE x
PF
MA(F) 0
FT AB sin 300 P AD F AE 0
(3)
由(3)解得
FT
2P 3F 4sin 300
24 310 4 0.5
19
kN
y
以FT之值代入式(1)、(2)，可得： FAx A
FAx=16.5 kN, FAy=4.5 kN。
FAy
y FAx A
Fx 0.
FAy
注：AB的连线不能与x轴垂直。
MA(F) 0
FT AB sin 300 P AD F AE 0
MB(F) 0
P DB F BE FAy AB 0
Fx 0
FAx 0
FT
300
B
DE x
PF
（1） （2） （3）
三矩式：
M A (F ) 0, M B (F ) 0, M C (F ) 0.
C
A 2m
300
B
D1m
E 1m
PF
解：(1) 取AB梁为研究对象。
y
(2) 画受力图。 未知量三个：FAx、FAy、FT ， FAx A
独立的平衡方程数也是三个。
FAy
(3) 列平衡方程，选坐标如图所示。
Fx 0
FA x FT cos 300 0
(1)
Fy 0
FA y FT sin 300 P F 0 (2)
平面一般力系的平衡
平面一般力系平衡的充分必要条件是：力系的 主矢和对任意一点的主矩都为零，即：
FR 0 , MO 0
FR′ O MO
平面一般力系的平衡方程为：
Fx 0, Fy 0, M O (F ) 0.
例题
图示一悬臂式起重机简图，A、B、C处均为光滑
铰链。均质水平梁AB自重 P = 4 kN,荷载 F =10 kN,有关 尺寸如图所示，BC杆自重不计。求BC杆所受的拉力 和铰链A给梁的约束力。
FT
300
B
DE x
PF
即铰链A处约束力的大小及与x轴正向的夹角为：
FA FA2x FA2y 17.1 kN
arctan FA y 15.30
FA x
思考题？
y FAx A
FAy
FT
300
B
DE x
PF
还有没有其他的求解方法？
方法二（二矩式）：
M A (F ) 0, M B (F ) 0,
注：A、B、C三点不能在同一直线上。