当前位置：文档之家 › 溶液的化学势、逸度、逸度系数ppt课件

溶液的化学势、逸度、逸度系数ppt课件

  • 格式：ppt
  • 大小：603.00 KB
  • 文档页数：8

下载文档原格式

  / 8

合集下载

逸度和逸度系数计算ppt课件

逸度和逸度系数计算ppt课件
9
逸度系数与P-V-T的关系
（1）以T，P为独立变量的逸度系数与P-V-T的关系
因G
G0ig
RT
ln
f p0
而 G G0ig
RT
ln
p p0
1 RT
p V 0
RT p
dp
P = P0 时，则：
ln
ln
f p
1 RT
p V 0
RT p
dp
只需EOS 便可计
算
10
RTd ln f Vdp (恒T时)
dGi RTd ln fˆi
Giig (T , p,y ) ln pyi
Gi (T ,
p,y
)
Giig (T ,
p,y
)
RT
ln
fˆi pyi
引入逸度系数的定义
ˆi
fˆi pyi
limˆ
p0
i
1
fˆi pyiˆi
6
混合物的逸度与其组分逸度之间的关系
•纯物质的逸度
fi
•混合物的逸度
f
•混合物中组分的逸度
2、组分逸度系数的计算
（1）对于V=V（T，P）型状态方程：
lnˆi
1 RT
p V i RT dp
0
P
（2）对于P=P（T，V）型状态方程：
lnˆ i
1 RT
Vt
RT
Vt
p ni
T ,Vt ,ni
dVt
ln Z
19
SRK、PR方程的组分逸度系数公式
状态 方程
组分逸度系数
SRK
dG i RTd ln fˆi lpim0 fˆi pyi
（T一 定 ）

化工热力学 课件 第4章-溶液热力学基础

化工热力学 课件 第4章-溶液热力学基础
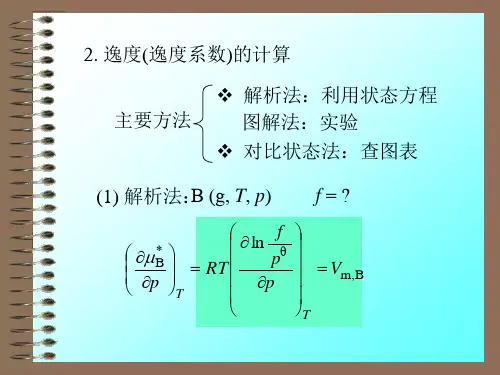
4.4.1定义
⎧dGi = RTd ln fi (恒T ) ⎪ 定义 1 dGi = RTd ln fi (T 一定) (式A) fi ⎨ =1 ⎪lim ⎩ p →0 p
纯物质 混合物中组分的逸度
⎧dGi ⎪ ˆ (T 一定) (式B) 定义2 ⎨ dGi = RTd ln f i ⎪lim ⎩ p →0
T，p 保持不变 ， 容易实现
定义偏摩尔性质：
规定在T，p,｛n｝≠i一定条件下，总容量性质（Mt）对于i组分摩 尔数(ni)的偏导数称为偏摩尔性质。
⎛ ∂M t ⎞ ⎛ ∂ ( nM ) ⎞ =⎜ Mi =⎜ ⎟ ⎟ ∂ ∂ n n i ⎠T , p ,n j [ i ] i ⎝ ⎝ ⎠T , p ,n j [ i ] ( M = V , U , H , S , A , G , cV , c p ...)
ˆ L = f L x γ (T , p, x , x ," , x ) f i i i i N 1 2
L ⎛ ⎞ p V s s i = pi ϕi xiγ i (T , p, x1 , x2 ," , xN ) exp ⎜ ∫ s dp ⎟ pi RT ⎝ ⎠
本章主要内容
4.1 均相敞开系统的热力学关系 4.2 偏摩尔性质 4.3 偏摩尔量与摩尔量间的关系 4.4 混合物中组分的逸度和逸度系数 4.5 理想溶液和理想稀溶液 4.6 活度系数定义及其标准态 4.7 混合过程性质变化 4.8 过量性质 4.9 活度系数模型
∑ ( x dM )
i
i T,p
=0
对于二元系统，在恒T、恒p下有
x1dM 1 + x2 dM 2 = 0
上式改写成：
dM 1 dM 2 = − x2 (1 − x2 ) dx2 dx2

大学物理化学第三章化学势

大学物理化学第三章化学势

物质的量分数，又称为摩尔分数，无量纲。
2. 质量摩尔浓度mB
mB def
nB mA
溶质B的物质的量与溶剂的质量之比称为溶质B的质
量摩尔浓度，单位是 mol kg-1 。
上一内容 下一内容 回主目录
返回
2021/2/14
溶液组成的表示法
3. 物质的量浓度cB
cB def
nB V
溶质B的物质的量与溶液体积V的比值称为溶质B的物质的量
化学平衡的条件是：除系统中各组分的温度和压力相等外，还 要求产物的化学势之和等于反应物的化学势之和。
总结：在等T,p W ' 0 的条件下，传质过程朝化学势降低的方向 进行，平衡时化学势相等—化学势判据（所有判据的统一）
上一内容 下一内容 回主目录
返回
2021/2/14
五、化学势与温度和压力的关系：
上一内容 下一内容 回主目录
返回
2021/2/14
三、化学势的物理意义
定温定压下， dG SdT Vdp BdnB BdnB
若不做非体积功：
BdnB < 0 自发过程
BdnB 0 平衡
物质的化学势是决定物质传递方向和限度的强度
因素，这就是化学势的物理意义。(等T , p,W ' 0)
dU TdS pdV
U ( nB
)S ,V ,nC
dnB
令：H f (S, p, nB , nC ...)
dH TdS Vdp
H ( nB )S , p,nC dnB
令：A=f(T,V,nB , nC ...)
dA SdT pdV
A ( nB )T ,V ,nC dnB
上一内容 下一内容 回主目录

化学势与逸度PPT课件

化学势与逸度PPT课件

(chemical potential for ideal gases and their
mixtures —— adopting the thermodynamic
standard state of gases as the reference state)
纯理想气体(pure ideal gases)
理想气体恒温混合的熵变：先利用化学位计算吉氏 函数变化，再对吉氏函数关于温度求导。
n(1) i
,
p(1)
ni(2) , p(2)
ni( ) , p( )
ΔG
n1 n2 nK , p
G初
K
n( ) ( ) ii
K
ni(
)
i
1 i1
1 i1
RT
ln
p( ) yi( ) p
G末
理想气体 理想气体混合物 实际气体、液体、固体 实际气液固体混合物
f
i
pi
p
fi pi pyi
f
i
pi
i
p
i
fi pii pyii pxii
3.逸度的性质和意义(properties and meanings of fugacity) 强度性质，状态函数
fi fi (T , p, x1 , x2 ,, xK 1 )
ni RT
ln
pyi p
id i
G ni
T , p,nji
i
(g) RT ln pyi p
纯理想气体
id i
i
(g) RT ln p p
理想气体混合物
p
pi pyi
id i
i
(g) RT ln pi p

逸度与逸度系数 ppt课件

逸度与逸度系数 ppt课件

对 真 实 气 体 ， 为 保 存 dGi=RTdlnP 简 捷式，同时又要使公式和事实符合，
G.N.lewis提出以逸度f代替压力P，有：
dGi=RTdlnfi
等温
其中，fi:纯组分i的逸度
这样，即保持了简单形式，又可运 用于真实气体。
对上式不定积分（等温下），
G质i=GGi=i0+Ri T）lnfi或
P Pis
Vil dp RT
由 fi s Pis is
fil Pis
P Vil dP
s
PiS RT
e i
或
fil
fis
fil fis
l
而f e i
P Pis
Vil d RT
P
fis
结论：
纯 液 体 在 T，P 时 的 逸 度 为 该 温
度下的P i s乘以两项校正系数。
（1）Φis 用来校正饱和蒸汽对理
i
。
在等温下，从基态积分到所处压
力P，即从f i 0积至 fi ，有:
ln
=Hi
ff i i0T=SiR1T
Gi
Gi0 又 得：
Gi=
，
G i 0 Hi0 TSຫໍສະໝຸດ i0ln f i f i0
R 1Hi THi0
Si
Si0
若基态的P0很低，即可认为是
理想气体，则 f 0 = P*
则有：ln
RT
V V0 b T 0.5 V0 V V b
V
PdV
RTln V b
V0
V0 b
a bT0.5
lnVV0•VV0bb
上式由A B1 , 得 A A V b B V1 VV bV (V b ) V (V b )V (V b )V (V b )

化工热力学：2.3 逸度系数和逸度

化工热力学：2.3 逸度系数和逸度

lni
P Zi 1dP 1
0P
RT
P 0
(Vi
RT P
)dP (1)
立方型 EOS均是以压力为显函数，故用(1)式不方便。 改成以T，V为独立变量的计算逸度系数的方程(2).
lni
Zi
1
ln
Zi
1 RT
V V0
(P
RT Vi
)dVi ( 2)
求R-K方程的逸度系数形式，教材P.34
)dP
P Pis
(Vi L
RT P
)dP
vapor fiV
RT
ln
fi S Pi S
P Pis
Vi
L
dP
RT
ln
P Pi s
liquid
fi L
VLE时；
V i
L i
i0 RT ln fˆiV i0 RT ln fˆiL
fiV fiL fiS
16
iS
fi S Pi S
整理得fi L PiSiS exp
27
6.694
ln fi Pi*
1 [Hi R
T
H
* i
（Si
Si*）]
18.016[ 2827.9 2879.5 （6.694 8.9037）] 4.5515
8.314 200 273.15
fi 94.77 Pi*
fi 9.48bar
i
fi Pi
9.48 0.948 10
9
§2.3.2.3 由状态方程计算纯物质的逸度系数
Ml
Mg
M
指饱和蒸汽在湿蒸汽 中 所 占 的mol或wt )
M V , U , H , S , A ,G , CV , CP ,

Roult定律,理想溶液

Roult定律,理想溶液
4. Gibbs函数减少
ΔmixG RT nA ln xA nB ln xB
设 sln
g
sln
T，p，xB，…
则
B (s ln )
B(g)
θB
RT
ln
pB pθ
(理想气体)
θB
RT ln
p*BxB pθ
(理想溶液)
θB
RT ln
p*B pθ
RT ln
xB
B g,T, p*B RT ln xB
B* l,T, p RT ln xB
(1)
Bsln B* l,T, p RT ln xB (1)
➢ Newton图
用法：B (g, T, p) = ?
查
Tc
Tr
T Tc
a
pc
pr
p pc
b
在Tr = a 的等对比温度线上，横坐标
为b，查出纵坐标 值。
(3) 求算f的意义： 解决了实际气体比较化学势的问题
解决了实际气体各种过程的计算：
例如：理想气体 He (T, p1) 等T 膨胀
G nRT ln p2
ΔmixH H2 H1
nAHA nBHB nAHm,A nBHm,B
nA HA Hm,A nB HB Hm,B (1)
ΔmixH nA HA Hm,A nB HB Hm,B (1)
A θA RT ln xA
p
pθ Vm,Adp
A A* l,T, p RT ln xA
T
A
T
p,xA
T
* A
T
p,xA
R ln xA T
p,xAHA T2源自H T* A2
0
HA HA*

溶液ppt课件

溶液ppt课件

旳化学势，它不是原则态。
上一内容 下一内容 回主目录
2024/9/28
溶质旳化学势
Henry定律因浓度表达措施不同，有如下三种形式：
pB kx xB kmmB kccB
(1)B (T , P) B (T ) RT ln(PB / P )
B (T ) RT ln(Kx / P ) RT ln xB
2024/9/28
溶质旳化学势
上一内容 下一内容 回主目录
2024/9/28
4.7 稀溶液旳依数性
依数性质：（colligative properties）当把一种不挥发
性物质溶于某一溶剂，构成稀溶液时，该溶液旳某些 性质只与溶质旳质点数（即多少）有关，而与溶质本 身旳性质无关，我们把稀溶液旳此种特征称为“依数 性”。 依数性旳种类：
2024/9/28
4.2 溶液构成旳表达法
4.质量分数wB（mass fraction）
wB
WB W (总)
溶质B旳质量与溶液总质量之比称为溶 质B旳质量分数。为无量纲量。
上一内容 下一内容 回主目录
2024/9/28
4.3 稀溶液中旳两个经验定律
拉乌尔定律（Raoult’s Law）
1887年，法国化学家拉乌尔在屡次试验旳基础上总
p)
(T
,
p
)
RTIn
P P
纯物质旳摩尔吉布斯自由能等于化学势
(T ,
P)
(T ,
P
)
RT
ln
P P
上一内容 下一内容 回主目录
2024/9/28
理想气体旳化学势
(T ,
P)
(T ,
P
)
RT

溶液的化学势逸度逸度系数ppt课件

溶液的化学势逸度逸度系数ppt课件

§8-2 溶液的逸度、逸度系数
混合物组分i的逸度1）．fˆi 混合物中组分i的逸度。
d G i RTd ln fˆi y i 是混合物组分i的摩尔分数。
lim fˆi 1  2）．fˆi对ig于理想y气iP体： pi
P 0 yiP
p i 称作理想气体的分压。真实气
体没有分压概念。  3）．
引言
但是在实际热工工程中，常会碰到几种纯质液 体或气体组成的系统。这种系统中，如果发生 相变或化学反应，那么系统热力状态的变化可 能伴随有质量及成分的变化。这是系统的广延 热力性质和构成系统的各种物质的摩尔数有关， 而不仅仅是两个独立状态参数的函数
§8-2 基本概念
什么是溶液？
溶液是由至少两种物质组成的均一、稳定的混 合物，被分散的物质（溶质）以分子或更小 的质点分散于另一物质（溶剂）中。物质在 常温时有固体、液体和气体三种状态。
1982溶液的逸度逸度系数2082溶液的逸度逸度系数2182溶液的逸度逸度系数2282溶液的逸度逸度系数溶液性质偏摩尔性质二者关系lnln2382溶液的逸度逸度系数为了解决混合物特别是液体混合物的组分逸度的计算问题对于每一个系统都选择一个与研究状态同温同压同组成的理想混合物理想溶液作参考态提出理想混合物的概
§8-2 溶液的逸度、逸度系数
fˆ (nlnf)
ln yi

ni
T,p,nj
lnˆi (nnlni )T,p,nj
∵
(nM)
Mi
ni
T, p,nj
ln
fˆ

是
ln
f
的偏摩尔性质
yi
ln ˆi  是 ln  的偏摩尔性质
ln x ilˆ i n

《理想溶液体系》课件

《理想溶液体系》课件

理想溶液体系的热力学 性质如何计算？
理想溶液体系的热力学属性 可以通过Raoult定律和Henry 定律进行计算和描述。
活度和逸度
1 活度和逸度的定义
活度是衡量溶液中各组分的实际浓度与标准浓度之间的比值，逸度是衡量溶液蒸汽压与 标准蒸汽压之间的比值。
2 活度系数和逸度系数的计算公式
活度系数和逸度系数可以通过各组分的逸度和活度计算公式得出。
3
理想混合热和偏摩尔焓的计算公式
理想混合热和偏摩尔焓可以通过热力学公式计算得出，用于揭示溶液中成分间的 相互作用。
理想溶液体系的应用
热力学性质在实际中的应用 应用实例介绍
理想溶液体系的热力学性质在溶 液制备、化学反应等领域具有重 要应用价值。
通过实际案例介绍理想溶液体系 在化学工业等领域的重要应用。
3 活度和逸度的作用和意义
活度和逸度是理解溶液的混合行为和热力学性质的重要指标，影响着化学反应和物质迁 移现象。
理想溶液体系的模型
1
热力学模型和实验模型
理想溶液体系的研究可以通过热力学模型和实验模型来进行，以定量描述其性质 和行为。
2
Raoult定律和Henry定律
Raoult定律适用于无限稀释溶液的情况，Henry定律适用于总溶质浓度较低的情 况。
《理想溶液体系》PPT课 件
理想溶液体系是研究溶液中成分间理想混合状态的体系，本课件将介绍其概 念、特点、热力学性质、活度与逸度、模型、应用以及未来研究方向。
概念介绍
什么是理想溶液体系？
理想溶液体系是指在相同温 度下，溶质和溶剂之间形成 理想混合状态的溶液。
理想溶液体系的特点是 什么？
理想溶液体系的特点是能够 表现出简单的热力学性质， 成分间相互作用力较小，没 有特异性相互作用。

第4章 第2讲 逸度与逸度系数讲解

第4章 第2讲 逸度与逸度系数讲解

-2-
2018年12月2日星期日
纯组分的逸度和纯组分的逸度系数
dG Vdp SdT
等温条件下应用于1mol纯流体i：
dGi Vi dP
 对于理想气体：
RT dGi dP dGi RTd ln P P
-3-
2018年12月2日星期日
纯组分的逸度和纯组分的逸度系数  对于真实气体，定义fi，令
-9-
f P
2018年12月2日星期日
 总结
 至此，已有三种逸度，纯物质逸度系数，混合物中组 分i逸度及混合物总逸度  相应地也有三种逸度系数  当混合物的极限组成=1时， 和 都等于 i i  对于理想气体：
f
ˆ f
f
fi
ˆ fi
f
-10-
2018年12月2日星期日
 液体的逸度
 理解一个概念：
id 0 ˆ f i xi f i
ˆ i xi a
ˆ ˆi a f i i id ˆ xi f i
 活度与摩尔分数之比；组分在溶液中的真实逸 度与理想溶液中的逸度之比
-23-
2018年12月2日星期日
 各组分逸度等于同温同压下各纯组分的逸度与它的 摩尔分数乘积的溶液是理想溶液。
 理想气体：分子间没有相互作用力，分子本身没有 体积
-21-
2018年12月2日星期日
 理想溶液各组分偏摩尔性质与它们的纯物质性质关系：
Vi Vi、 U i U i、 Hi Hi Gi Gi RT ln xi S i S i R ln xi
-14-
2018年12月2日星期日
总结
溶液性质 偏摩尔性质 二者关系式

溶液的化学势、逸度、逸度系数

溶液的化学势、逸度、逸度系数

§8-2 溶液的化学势
什么是化学势？
化学势：闭口系中驱使物质改变的势叫化学势。
§8-2 溶液的化学势
u 意义： i 表示系统成分不变是，在T、p不变
或T、V不变，或S.p不变或S、V不 变的条件下，相应的自由焓，自由 能、内能随第i种ui 组成摩尔数ni的变 化率。假想有一个S、V不变而溶液 总摩尔数n为无限大的系统。这时 加入摩尔i组成并不影响溶液的变化， 而系统的内能却增加了。这增加的 内能就是系统中i组成的化学势。
§8-2 溶液的逸度、逸度系数
 混合物组分i的逸度系数
ˆ fˆi
i
y Pi
§8-2 溶液的逸度、逸度系数
 混合物的逸度  混合物的逸度系数
dG RTd ln f lim f 1
P0 P
f
P
§8-2 溶液的逸度、逸度系数
 至此，已有三种逸度，纯物质逸度系数，混合物中组
分i逸度及混合物总逸度
引言
但是在实际热工工程中，常会碰到几种纯质液 体或气体组成的系统。这种系统中，如果发生 相变或化学反应，那么系统热力状态的变化可 能伴随有质量及成分的变化。这是系统的广延 热力性质和构成系统的各种物质的摩尔数有关， 而不仅仅是两个独立状态参数的函数
§8-2 基本概念
什么是溶液？
溶液是由至少两种物质组成的均一、稳定的混 合物，被分散的物质（溶质）以分子或更小 的质点分散于另一物质（溶剂）中。物质在 常温时有固体、液体和气体三种状态。
 相应地也有三种逸度系数
f  当混合物的极限组成=1时， 和
 对于理想气体：
fˆi 都等于 f i
f i fˆi f
§8-2 溶液的逸度、逸度系数
 理解一个概念：  气液两相处于平衡时，饱和蒸汽

16 气体化学势,逸度

16 气体化学势,逸度

B* － B
(2) B*值不可知，但不影响比较化学势
(3) 可由统计力学导出
2. 理想气体混合物
B+C+… T，pB 纯B T，pB*
平衡： (1) pB = pB* (2) B = B*
B = ?
semipermeable membrane of B
* pB p * θ θ B B B B RT ln θ B RT ln θ p p
G ( S ) n T n p ,nB ,nC , B T , p ,nC , B T , p ,nC ,
B SB T p,nB ,nC ,
意义：T↑， B↓
B(T，p )的化学势之差。
意义：各种实际气体的化学势表达式整 齐化一，且与理想气体的形式相同。
三、气体的逸度和逸度系数 (Fugacity and fugacity coefficient)
1. 逸度和逸度系数的意义：
f p
f p
校正压力 fugacity coefficient
(fugacity factor, )
(1) 对理想气体： 不需要校正， = 1 or
f=p
(2) 对实际气体： ≠ 1，反映气体在热力学上对理想气 体的偏离程度 lim f p lim 1 or
p 0
p 0
(3) 对标准状态：
= 1，f = p = 101325 Pa
(4) = (T, p, 本性)：
2. B与p的关系：
B 同理： VB 意义：一般p↑， B↑ p T ,nB ,nC ,
dB SBdT VBdp

逸度和逸度因子的求取PPT课件

逸度和逸度因子的求取PPT课件

了解一下：用状态方程计算逸度因子
如果是流体混合物，状态方程形式仍然不变，范德华方程 与纯物质相同：
RT a p Vm b Vm2
“混合”主要体现在方程参数a和b与组成 xi 的函数关系上， 称为混合规则，比如，常用的一种混合规则
K
b bi xi ; bi是纯i组分的范德华参数b i 1
KK
dp
p T
Vm
dT
p Vm
T
dVm
温度恒定 dp
p Vm
T
dVm
积分上下限也必须作相应改变，压力为零时，对应的体积
为无穷大，当压力为体系压力时，对应的体积应该分别由
实际流体状态方程和理想气体状态方程计算得到：
了解一下：用状态方程计算逸度因子
例：纯范德华流体的逸度因子
RT a p Vm b Vm2
lni
ln
f
i
p
1 RT
p 0
Vi
RT p
dp
混合物
lni
ln
fi p
1 RT
p RT
0
Vi
p
dp
了解一下：用状态方程计算逸度因子
例：纯范德华流体的逸度因子
RT a p Vm b Vm2
流体的状态方程一般取体积而不是压力为独立变量，计算 逸度因子时，积分变量必须由压力换成体积：
a
aia j xi x j ; ai是纯i组分的范德华参数a
i1 j1
有了混合规则，就可以由状态方程导出偏摩尔体积表达式，
如同纯物质一样计算逸度系数了。
lni
ln
RT
bi
p[Vm (T , p) b] Vm (T , p) b
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

M (xiMi )
ln f
fˆ ( yi ln yi )
ln (yi lnˆi )
20
§8-2 溶液的逸度、逸度系数
有三种逸度及逸度系数：
纯组分的逸度：fi 混合物的逸度：f
溶液中组分的分逸度：fˆi
纯组分的逸度系数：i 混合物的逸度系数：
溶液中组分的分逸度系数：ˆi 21
§8-2 溶液的逸度、逸度系数
分i逸度及混合物总逸度
 相应地也有三种逸度系数
f  当混合物的极限组成=1时， 和
 对于理想气体：
fˆi 都等于 f i
f i fˆi f
17
§8-2 溶液的逸度、逸度系数
 理解一个概念：  气液两相处于平衡时，饱和蒸汽
的逸度与饱和液体的逸度相等。
18
§8-2 溶液的逸度、逸度系数
ln
6
§8-2 溶液的化学势
由此可见，化学势是溶液中组成的热力性质。i 组成的化学势是溶液系统在某些特定条件下， 作为该系统的特征函数的广延量参数 对改组成 摩尔数的变化率。化学势的单位是J/mol
7
§8-2 溶液的化学势
之所以称为化学势，是因为 它是组成的化学能位 的量度。温差是传递热量的驱动力，压差是传递 容积功的驱动力，而化学势差是驱动传递质量的 驱动力。
 注：  fi单位于压力的单位相同。 无因次  逸度的物理意义：逸度表征体系的逃逸趋势，
校正压力。 §9-2 溶液的逸度、逸度系数  理想气体的逸度系数等于1，真实气体的逸度系
数可以大于1，也可以小于1，它是温度、压力 的函数。  逸度的推导条件是等温条件。
13
§8-2 溶液的逸度、逸度系数
8
§8-2 溶液的逸度、逸度系数
什么是逸度？
在相平衡计算中，离不开逸度及逸度系 数计算。 逸度可理解为有效压力，它的单位 与压力相同。它表示了物质的逸散程度。 逸度（系数）包括三种，即：纯组 分的逸度及纯组分的逸度系数；溶液中组 分i的逸度及溶液中组分i的逸度系数；混 合物的逸度及混合物的逸度系数
9
§8-2 溶液的逸度、逸度系数
dG Vdp SdT
等温条件下应用于1mol纯流体i：
dGi VidP
对于理想气体：
dGi
RT P
dP
dGi
RTd ln
P
10
§ 8-2 溶液的逸度、逸度系数
 对于真实气体，定义fi，令
dGi RTd ln fi
∵
dGi
RT p
dP
dGi
RTd
ln
P
RTd ln fi RTd ln P fi c P，c为常数
14
§8-2 溶液的逸度、逸度系数
 混合物组分i的逸度系数
ˆ fˆi
i
y Pi
15
§8-2 溶液的逸度、逸度系数
 混合物的逸度  混合物的逸度系数
dG RTd ln f lim f 1
P0 P
f
P
16
§8-2 溶液的逸度、逸度系数
 至此，已有三种逸度，纯物质逸度系数，混合物中组
4
§8-2 溶液的化学势
什么是化学势？
化学势：闭口系中驱使物质改变的势叫化学势。
5
§8-2 溶液的化学势
u 意义： i 表示系统成分不变是，在T、p不变
或T、V不变，或S.p不变或S、V不 变的条件下，相应的自由焓，自由 能、内能随第i种ui 组成摩尔数ni的变 化率。假想有一个S、V不变而溶液 总摩尔数n为无限大的系统。这时 加入摩尔i组成并不影响溶液的变化， 而系统的内能却增加了。这增加的 内能就是系统中i组成的化学势。
（理想溶液）作参考态，提出理想混合物的概
念。
23
`.
2
引言
但是在实际热工工程中，常会碰到几种纯质液 体或气体组成的系统。这种系统中，如果发生 相变或化学反应，那么系统热力状态的变化可 能伴随有质量及成分的变化。这是系统的广延 热力性质和构成系统的各种物质的摩尔数有关， 而不仅仅是两个独立状态参数的函数
`.
3
§8-2 基本概念
什么是溶液？
溶液是由至少两种物质组成的均一、稳定的混 合物，被分散的物质（溶质）以分子或更小 的质点分散于另一物质（溶剂）中。物质在 常温时有固体、液体和气体三种状态。
高等热力学
第八章 溶液的热力性质 第二节 溶液的化学式、逸度、逸度系数
`.
1
引言
之前几关系章中介绍的流体p-v-T关系及其他热力 性质的推算方法，研究对象限于单相、简单可压 缩、定成分、定质量的闭口系统。也就是说分析 对象若是纯质，则取纯质气相或液相，并且做功 方式只有膨胀功的闭口系为分析计算对象。但是 如果分析对象为几种纯质组成的混合物，则除了 单相及只有膨胀功的闭口系条件之外，还要求是 定成分，及即闭口系内系统不发生化学反应。
 令c=1，即理想气体的逸度等于压力。
11
§ 8-2 溶液的逸度、逸度系数
得到：
dGi RTd ln fi lim fi 1
P0 P
 纯组分逸度定义式
 fi为纯组分i的逸度，单位为压力的单位。当压力为
零时，真实气体状态表现出理想气体的性质。
 纯组分的逸度系数
i
fi P
12
§8-2 溶液的逸度、逸度系数
fˆ yi
(n ln ni
f ) T , p,nj
ln ˆi
(n ln )
ni
T , p,nj
∵
Mi
(nM )
ni
T , p,nj
ln
fˆ

yi
是
ln f 
的偏摩尔性质
ln ˆi  是 ln  的偏摩尔性质
19
§8-2 溶液的逸度、逸度系数
 根据摩尔性质与偏摩尔性质的关系式：
混合物组分i的逸度1）．fˆi 混合物中组分i的逸度。
dGi RTd ln fˆi yi 是混合物组分i的摩尔分数。
lim fˆi 1 P 0 yi P
 2）．fˆi对ig于理想yi气P体： pi
p i 称作理想气体的分压。真实气
体没有分压概念。
 3）．
P yiP pi P yi
溶液性质
偏摩尔性质
二者关系
M
Mi
M xiMi
ln f
ln ˆfi
xi
ln f
xi
ln
ˆfi xi
ln
ln ˆi
2 溶液的逸度、逸度系数
 理想混合物的提出

为了解决混合物特别是液体混合物的组分
逸度的计算问题，对于每一个系统都选择一个
与研究状态同温、同压、同组成的理想混合物