当前位置：文档之家 › 第一章函数,极限与连续PPT课件

第一章函数,极限与连续PPT课件

  • 格式：pptx
  • 大小：765.45 KB
  • 文档页数：40

下载文档原格式

  / 40

合集下载

高等数学第1章 函数、极限与连续PPT科技

高等数学第1章 函数、极限与连续PPT科技
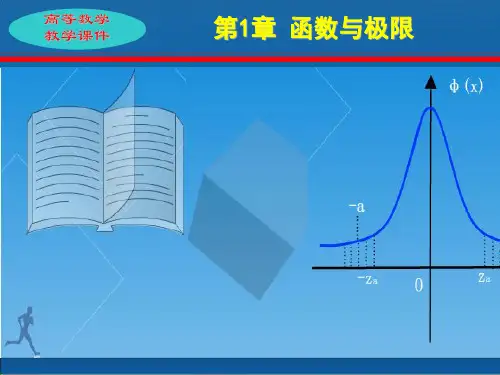
狄利克雷函数
( 一般指最小正周期 ).
周期为
1, x 为有理数
0 , x 为无理数
4.有界性
x D , M 0 , 使 f ( x) M ,称 f (x)为有界函数. x I , M 0 , 使 f ( x) M , 称 f (x) 在 I 上有界.
说明: 还可定义有上界、有下界、无界.
三、函数的简单性质
设函数 y f (x) , x D , 且有区间 I D .
1.单调性
x1, x2, f (Ix, )x当1Mx2,时称， 为有上界
y
若
f
(
x1 )
f
,M
(x2
)f,(称x
),f
称( x为) 有为下I 界上的
单调增函数 ;
若若f对(x任1意) 正数f (Mx2, )均, 存称在 f ( x) 为
证: 由 f (x) 的对称性知
f (a x) f (a x), f (b x) f (b x)
于是
f (x)
f (2a x)
故 f (x) 是周期函数 , 周期为
02
第2节
数列的极限
一、数列极限的例子
二 、数列与整标函数
三 、数列的极限
四 、数列极限的性质
一、数列极限的例子
极限概念是由求某些实际问题的精确解答而产生的．例如，要计算 由曲线y＝x2和直线y＝0，x＝1围成的“曲边三角形”的面积A.
并可用一个式子表示的函数 , 称为初等函数 . 否则称为非初等函数 .
例如 ,
y xx, ,
x 0 可表为 x0
y
x2 , 故为初等函数.
又如 , 双曲函数与反双曲函数也是初等函数 .
非初等函数举例: 符号函数

第1章函数极限与连续课件

第1章函数极限与连续课件

.
.
o
.
1
.
2
.
x
“ x ” 数
实数集是连续的或完备的。
在高等数学中，数与点 说成 “ x ” 点 ，反之亦然 .
不加区别，常将
3.常用不等式:
x , 绝对值 : x R , x x ,
x0, x0.
1 . x R, x 0 .
o
2 . x R, x x x .
事实上，若 l 为 f ( x ) 的一个周期 , 则
f ( x ) f ( x l ) f [( x l ) l ] f ( x 2l ) f ( x nl ) . nl ( n N ) 也是 f ( x ) 的周期 .
若 在周期函数 f (x ) 的所有周期中存在 最小的正 周期T ， 则称这个最小正周期 T 为 f ( x ) 的 基本周期 . 通常我们所说的函数的 周期都是指基本周期 .
{ x 0 x x0 } ( x0 , x0 ) ( x0 , x0 ) .
x0
x0
x0
x
1.1.2 函数的概念
一. 函数的定义 定义 设给定两个非空实数集 D 和 M . 若 x D, 按照某种对应法则 , 对应 唯一确定 f 的一个实数 y M , 则称 f 是定义在 D 上的函数， 表示为： f : D M ( x y f ( x) )
o
3 . x h ( h 0) h x h .
o
4 o . x h ( h 0) x h 或 x h .
5 . x , y R , x y x y x y .

高等数学(上册)第一章函数、连续与极限课件

高等数学(上册)第一章函数、连续与极限课件

9
2.区间
第一章 函数、连续与极限
数集 x a x b 及x a x b 称为半开区间，分别记作 a,b 和 a,b (见图1-9
和图1-10）.
[a,b)
(a,b]
a
图1-9
b
x
a
图1-10
b
x
以上这些区间都称为有限区间，数 b a 称为这些区间的长度. 从数轴上看，这些 区间是长度为有限的线段.
与 B 的并集（简称并），记作 A B ，即 A B {x | x A 或 x B}；
A AB B
A AB B
图1-2
图1-3
5
1. 集合及其运算
第一章 函数、连续与极限
由包含于 A 但不包含于 B 的元素构成的集合（见图 1-4），称为 A 与
B 的差集（简称差），记作 A \ B ，即 A \ B {x | x A 且 x B} ；
2
课前导读
集合
具有某种确定性质的对象的全体称为集合（简称集），组成集合的个别 对象称为集合的元素. 习惯上，用大写英文字母 A, B,C, 表示集合，
用小写字母 a,b, c, 表示集合的元素. a A 表示 a 是集 A 的元素 （读作 a 属于 A ）， a A 表示 a 不是集 A 的元素（读作 a 不属 于 A ）. 集合按照元素的个数分为有限集和无限集 ，不含任何元素的
集合称为空集，记为 .
3
一、 集合的概念
第一章 函数、连续与极限
我们把自然数的全体组成的集合称为自然数集，记作 . 由整数的全体
构成的集合称为整数集，记为 . 用 Q 表示全体有理数构成的有理数集，R
表示全体实数构成的实数集. 显然有 Z Q R .

《函数的极限与连续》课件

《函数的极限与连续》课件

示例
考虑函数$f(x) = x^2$，在区间 $[0, 1]$上连续且单调增加。如果 $f(0) < c < f(1)$，则可以证明$c < frac{f(0) + f(1)}{2}$。
利用连续性求函数的零点
要点一
总结词
利用函数的连续性可以找到函数的零 点。
要点二
详细描述
如果函数在某区间上连续，且在该区 间上从正变负或从负变正，则可以利 用函数的连续性找到函数的零点。这 是因为函数在这一点上从增加变为减 少或从减少变为增加，的定义
函数在某点连续的定义
如果函数在某点的左右极限相等且等于该点的函数值，则函数在该点连续。
函数在区间上连续的定义
如果函数在区间内的每一点都连续，则函数在该区间上连续。
连续性的性质
连续函数的和、差、积、商（分母不为零）仍为连续函数。
复合函数在复合点连续的定义：如果一个复合函数在某点的极限等于该点的函数值，则复合函数在该点 连续。
与其他数学知识的联系
探讨函数极限与连续性与中学数学、微积分等其他 数学知识的联系，理解其在数学体系中的地位。
理论严谨性
深入思考函数极限与连续性理论的严谨性和 完备性，理解数学严密性的重要性。
对后续学习的展望
导数与微分
预告后续将学习函数的导数与微分概念，了解它们与 极限和连续性的关系。
级数与积分
简要介绍级数和积分的基本概念，理解其在数学中的 重要性和应用。
01
和差运算性质
若$lim f(x)=A$且$lim g(x)=B$ ，则$lim [f(x)pm g(x)]=Apm B$。
02
03
乘积运算性质
幂运算性质
若$lim f(x)=A$且$lim g(x)=B$ ，则$lim [f(x)cdot g(x)]=Acdot B$。

《函数的极限与连续》PPT课件

《函数的极限与连续》PPT课件

定量刻画之一：远近
刻画远近的工具——距离
x与x0的距离是 | x x0 | （ f x）与A的距离是 | （ f x） A |
计算 | a b | 的大小的“精确值” 几乎是不可能也是不可取的
因此，我们选择用| a b | 的 "精确度"来刻画，即若给定
一个精确度， 那么符合这个
精确度要求的数的全体为
极限存在左右极限存在并相等不存在第一类间断点第一类间断点第二类间断点第二类间断点??可去间断点可去间断点??跳跃间断点跳跃间断点??无穷间断点无穷间断点??震荡间断点震荡间断点第一类间断点第二类间断点可去间断点可去间断点无定义无定义值太高值太高值太低值太低跳跃间断点跳跃间断点无穷间断点无穷间断点震荡间断点震荡间断点哎呀哎呀不好不好
第二类间断点
无穷间断点 震荡间断点
情形1.1：f (x)在x0处无定义.
x自由地趋于x0
y
注意到：
在这种情形下，
lim f (x) A
x x0
存在，因此如果我们重 新定义
f (x)在x0处的值为
●
f (x0 ) A,
那么这个新的 f (x)在x0处连续.
这种间断点称为可去间断点.
O
x
哎呀,不好!有个洞, 还没 有支撑， 我掉下去了!!!
●
●
●
x0 x
x
情形 3：f ( x)在x0处有 或无定义. lim f ( x)
x x0
和 lim f ( x)至少有
x x0
一个为 或 或. 此时，直线
x x0 称为y f ( x)的渐进线.
这种间断点称为无穷间 断点
x x0
y
快救救我，我 要跑到未知世

高等数学 第一部分 函数、极限与连续 课件ppt

高等数学 第一部分 函数、极限与连续 课件ppt

a 1 时，y log a x 单调递增， y
y logax (a 1)
0 a 1时y， log a x 单调递减。 o
x
y logax (0 x 1)
1-1 函数
4. 三角函数
正弦函数：y sin x
定义域：(,)．
值 域：[1,1] ．
单调性：
在
2
2k , 2
2k
单调增加；2
1-1 函数
函数的表示法
1）以数学式子表示函数的方法叫公式法如： y x2, y cos x 公式法的优点是便于理论推导和计算．
2）以表格形式表示函数的方法叫表格法，它是 将自变量的值与对应的函数值列为表格，如三角函 数表、对数表等，表格法的优点是所求的函数值容 易查得．
3）以图形表示函数的方法叫图形法或图象法， 这种方法在工程技术上应用很普遍，其优点是直观 形象，可看到函数的变化趋势．
4
2
3
（2） y sin x cosx 的周期T 2
（3） y cos 2x tan x 的周期T 3 ．
3 3 6
1-1 函数
4．有界性
定义 1.6 设函数 y f (x) 的定义域为 D，如果存在 一个正常数 M，使得对于任意的 x D ，都有| f (x) | M , 则称函数 y f (x) 在 D 上有界．如果不存在这样的正常 数 M，即对任意的正常数 M，都存在某个点 x0 D ，使 得| f (x0 ) | M , 则称函数 y f (x) 在 D 上无界．
2k ,
3
2
2k
单调减少．
奇偶性：奇函数．
周期性：周期函数．
有界性：有界函数．
余弦函数：y cosx
1-1 函数

第1章 函数极限与连续PPT课件

第1章 函数极限与连续PPT课件
用集合形式可表示为：Rf={f(x)|x∈ D(f)}（通常Rf B）
上页 下页 返回
例：试求由下列公式定义的函数的自然定义域
f (x) 1 x(x 1)
解: Df {x| x0且 x 1 ,0 1,
上页 下页 返回
1.1.2 函数的图形
❖ 定义1.2 设f是定义在Df上的函数，它的图形是满足条件y=f(x)
上页 下页 返回
1.2.2 函数的复合运算
❖ 定义1.8 设函数 y f (u)和 u (x) 是两个已知和函数，对于
函数 的定义域 D 中的一些 x ，如果函数值 u (x) 在
函数f的定义域 D f 中，那么就可以计算得到一个对应的值 f ((x))，于是构成了一个新的函数 yg(x)f((x))，这个新
称函数f是在区间I上的单调增函数（或单调减函数），称I为f 的单调增（或减）区间。 单调增函数和单调减函数统称为单调函数。
从几何意义上看，单调增函数的图形是向右上方上升的 曲线；单调减函数的图形是向右下方下降的曲线。
上页 下页 返回
（3）函数的奇偶性 ❖定义1.5 设函数f的定义域 D f 关于原点对称，即当 x D f 时，必有 x D f 。若对于任意的 x D f ，总有 f(x)f(x)， 则称f是偶函数；若对任意的x D f ，总有f(x)f(x)，则 称f是奇函数。
从几何意义上看，偶函数的图形关于y轴对称，奇函数的 图形关于原点中心对称。
上页 下页 返回
（4）函数的周期性
❖ 定义1.6 设函数f的定义域是D f ，若存在非零数T，使对每个
x D f ，都有 xTDf ，且总有 f(xT)f(x)成立，则
称函数f为周期函数，数T称为周期函数f的周期。

第1章 极限与连续精品PPT课件

第1章 极限与连续精品PPT课件
第1章 极限与连续
第1章 极限与连续
1.1 初等函数 1.2 函数的极限 1.3 无穷小量与无穷大量 1.4 极限的运算 1.5 两个重要极限 1.6 函数的连续性 复习题1
第1章 极限与连续
1.1 初等函数
1.1.1 常量与变量 在观察某种自然现象或进行某项科学实验的过程中，
常涉及一些事物的数量变化情况. 例如， 一物体作匀速直 线运动， 那么时间与位移的大小都是变量， 而速度则为 常量. 又如， 一密闭容器内的气体在加热过程中， 需要考 虑容器内气体的体积V、 分子数n、 绝对温度T以及压力P， 其中体积V与分子数n两个数量在整个过程中保持不变， 而绝对温度T与压力P则不断变化.
1 x2 0
即1-x2＞0， 解之， 得-1＜x＜1. 所以定义域为 ｛x｜-1＜x＜1｝或记为(-1， 1).
第1章 极限与连续
(2) 函数是一个分式且分母开平方， 所以有sinx＞0 解之， 得2kπ＜x＜2kπ+π， k∈Z， 所以定义域D=
｛x｜2kπ＜x＜2kπ+π， k∈Z｝.
第1章 极限与连续
部分称为点x0的去心邻域， 可用不等式0＜｜x-x0｜＜δ
表示.
第1章 极限与连续
(x0－ δ,x0＋ δ)
O
x0－ δ
x0
x0＋δ
图 1-6
第1章 极限与连续
1.1.3 函数概念 在讨论函数的概念之前， 我们先来看几个实际生
活中的例子. 例 1 某会员制商店对会员购物提供优惠， 会员可
按商品价格的85%购买商品， 但每年需交纳会员费300 元. 问： 若某人只在此商店购物， 至少需购多少钱的 商品(按商品价格计算)才能真正受惠?一年内实际受惠 多少钱?

第一部分函数的极限与连续教学课件

第一部分函数的极限与连续教学课件
这 时 ,也 说 数 列 的 极 限 不 存 在 .
如 果 数 列 {an}收 敛 ,则 数 列 {an}的 极 限 唯 一 .
35
定义2 对 于 数 列 { a n } , 如 果 存 在 正 数 M , 使 得 一 切 a n 都 满 足 不 等 式
an M , 则 称 数 列 { a n } 是 有 界 的 .
12
求函数的定义域时应遵守以下原则： (1) 代数式中分母不能为零； (2) 偶次根式内表达式非负； (3) 对数中真数表达式大于零； (4) 反三角函数要根据各自的定义域； (5) 两函数代数和的定义域，应是两函数定义域的公共部分； (6) 对于表示实际问题的解析式，还应该保证符合实际意义.
13
3 x 2 0
3 x 3
x 1
解出 1 x 1
故不等式组的解为 . 1x1 因此，该函数的定义域为 [1,1]
11
例4 已知函数 y f (x) 的定义域是 [ 2,5] 求 f (2x1) 的定义域
例5 判断下列各对函数是否相同.
(1) fxx,gx x2
(2) f(x ) 1 ,g (x ) s in 2 5 x c o s 2 5 x
16
1.2 函数的特性
1. 函数的单调性 单调增加函数、单调减少函数、单调区间
17
例1
tan(cosx)sin(arcosx)1[cos(arcosx)]21x2. cos(arcosx) cos(arcosx) x
讨论函 y3数 x,yx2的单调 . 性
正切函数ytanx在区间[,]上的函数叫作反正切函数， 22
并记作{an},有时也简记作an.
x
29
4、三角函数
y sx , y i c n x , y o tx a s , y c n x , y o sx , t e y c c x 正弦函数 ysin x

高数函数极限与连续.ppt

高数函数极限与连续.ppt

2 7
3
x 4
x
5
x3 1
x3
2. 7
机动 目录 上页 下页 返回 结束
例4、
求
lim
x1
x
2
x2 1 2x
3
.
( 0型) 0
解：x 1时,分子,分母的极限都是零.
先约去不为零的无穷小因子x 1后再求极限.
lim
x1
x2
x2 1 2x
3
lim
x1
(x (x
1)( x 3)( x
1) 1)
yy y x2 当 x 0 时为减函数;
当 x 0 时为增函数;
o
xx
机动 目录 上页 下页 返回 结束
(3) 函数的有界性:
若X D, M 0,x X ,有 f ( x) M 成立, 则称函数f ( x)在X上有界.否则称无界.
y
y 1 x
在(,0)及(0,)上无界; 在(,1]及[1,)上有界.
2
2
2
机动 目录 上页 下页 返回 结束
例3、 设函数 f ( x) 1 , g( x) x 2
x 1
求 f [g( x)] 和g[ f ( x)] 解：f [g(x)] 1 1 ,
g(x) 1 x 2 1 g[ f (x)] f (x) 2 1 2
x 1
机动 目录 上页 下页 返回 结束
（或n ）的过程中, 对应函数值 f ( x)无限
趋近于一个确定常数 A.
lim
n
an
A
lim f ( x) A
x
lim f ( x) A
x
lim f ( x) A
x
定理 : lim f ( x) A lim f ( x) A且 lim f ( x) A.

高等数学(微积分学)教学课件

高等数学(微积分学)教学课件

三、两个重要极限
重要极限Ⅰ lim sin x 1 x0 x
它可以拓展为 lim sin[ f (x)] 1 f (x)0 f (x)
sin 2x
例：lim x 2x
1
1 cos x
lim
x0
x2
lim
x0
2 sin 2 x 2
4 x2 4
lim
1
sin
x 2
x0 2 x
2
2
1 2
判断：lim sin x 1
叫做因变量.
数集 D 称为这个函数的定义域.
全体函数值的集合称为函数的值域.
2. 函数的表示法
解析法（公式法）：用解析表达式（或公式）表示函数关系.
y x 1
表格法：用列表的方法来表示函数关系.
x123456789 y 1 4 9 16 25 36 49 64 81
图示法：用平面直角坐标系 xoy 上的曲线来表示函数关系.
x
x
1 0
x
x
1
1
1 lim( x0 1
x
)
1 x
x
lim
x0
(1 (1
x) x
1
x) x
lim x0
(1 x) x
1 (1)
[1 (x)] x
e e1
e2
一类特殊极限
若f
(x)
a0 xm a1xm1 a2 xm2 b0 xn b1xn1 b2 xn2
am1x am bn1x bn
x 果对于定义区间的任意点 , 恒有 f (x) f (x) , 则称f (x)
为 D 内的偶函数；如果恒有 f (x) f (x) , 则称 f (x)为D

第一章函数、极限与连续幻灯片课件

第一章函数、极限与连续幻灯片课件

lim fx lim x 1 2 ， l i m fx l i m s i n x 1 s i n 3 1 ，
x 3
x 3
x 3
x 3
因 为 lim fx lim fx ， 所 以 lim fx不 存 在 .
x 3
x 3
x 3
④ 利用两个重要极限求函数的极限。即若所求极限为形如
(2) 如果y f(x) 在(a，b) 内每一点连续
(3) 如果y f(x) 在(a，b) 内连续，
且 lim f(x) f(b)，lim f(x) f(b)
xb0
xa0
那么yf(x) 在点x0 连续 那么yf(x) 在(a，b) 内连续 那么yf(x) 在[a，b] 上连续
六、本章关键词
函数 极限 连续
② 利 用 函 数 的 连 续 性 求 函 数 的 极 限 ， 即 若 fx 在 x x 0 处 连 续 ， 则 有 x l im x 0fx fx 0 .
例 10 求lxi m 4x2 x5 x14. 解 因 为 函 数 x 2 x 5 x 1 4 在 x 4 处 连 续 ，
所 以 lxi m 4x2 x5 x 1 4f41 8.
0 形式的不定式，并且极限式中含有三角函数，一般通 0 过三角函数的恒等变换再利用重要极限 lim sin x 1 求
x0 x 极限；若所求极限为形如 1 形式的不定式，并且所求函
1
数易转化为 1 u u
或
1
1 u
u
的形式，通常采用
lim
x
1
1 x
x
e
求极限。
例 12求limsin7x . x0arcsin5x
例9 求下列极限：
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2、利用两个重要极限计算
lim sin x 1 x0 x
3、利用夹逼准则
lim(1 1 ) x e
x
x
4、利用等价无穷小等价替换求极限
5、利用洛比达法则（第四章）未定型 0 或 型极限
lim f (x) lim f (x)
0
xa g(x) xa g (x)
例1
求
lim(
n
1 n2
2 n2
n n2
3、无穷小量和无穷大量
若 lim f (x) 0,则称f (x)是极限过程x X下的无穷小量. xX
若 lim f (x) ,则称f (x)是极限过程x X下的无穷大量 xX
（2）无穷小量和无穷大量性质
1 无穷大
无穷小；
1 无穷小
无穷大
性质1 有限个无穷小的和仍是无穷小。
性质2 有界函数与无穷小之积是无穷小。
高等数学辅导
（北上专升本） 课时：32
第一章 第二章 第三章 第四章 第五章 第六章 第七章
函数、极限与连续 导数与微分 中值定理及导数应用 不定积分 定积分及其应用 微分方程 向量代数与空间解析几何
第一章 函数、极限与连续
一、函数
1、函数的二要素：定义域和对应法则 （1）、函数的定义域求解： 定义域是使得函数表达式有意义。课本P7
若f (x) f (x) 称 f ( x)为奇函数 ;
偶函数关于y轴对称, 奇函数关于原点对称
（3）函数的周期性 f ( x T ) f ( x) （4）函数的有界性
若X D, M 0, x X ,有 f ( x)
M 成立,
4、求解反函数（步骤） （1）反解：把x从方程f(x)中解出 （2）改写：在表达式x与y互换
（2）、判断两个函数是否相同
2、函数符号的理解和使用 直接代入法
变量代换法
对式子的直接加工法
3、函数的几何特性 （1）函数的单调性
y
y f (x)
f (x2 )
f (x1)
o
x
I
y
y f (x)
f (x1)
f (x2 )
o
x
I
（2）函数的奇偶性 设D关于原点对称 , 对于x D,
若f (x) f (x) 称 f ( x)为偶函数 ;
lim
x
2x3 7x3
3x2 4x2
5 1
lim
x
2 7
3
x 4
x
5 x3 1 x3
2. 7
(无穷小因子分出法)
小结:当a0 0, b0 0, m和n为非负整数时有
lim
x
a0 xm b0 xn
a1 xm 1 b1 xn 1
a0 当n m,
am
b0 0 当n m,
bn
当n m,
注意：上述公式只适用于x 且 函数为多项式相除的情况.
5、复合函数
y f (u) u ( x)
y f [( x)]
二、函数的极限
1.定义: 设x X时,f (x)无限趋于某一确定的数 A,则称 x X时,f (x)收敛于A,记 lim f (x) A,
xX
X的变化趋势有:
x x0包含两个过程 : x x0 , x x0
x 包含两个过程 : x ,x
利用洛比达法则（第四章）未定型 0 或 型极限 0
公式 lim f (x) lim f (x) xa g(x) xa g (x)
0
y=f(x)在点 U( x0, ) 处有界
2.夹逼准则 准则Ⅰ 如果在某个变化过程中满足下列条件:
(1) g(x) f (x) h(x) (n 1,2,3) (2) lim g(x) lim h(x) A,
那末 lim f (x) A.
例题：
例2 求 lim( 1 1 1 ).
推广 若x 0,
0,sin ~
ln(1 ) ~
例1
求 lim tan2 2x . x0 1 cos x
原式
lim x0
(2 1
x)2 x2
8.
2
注意 不能滥用等价无穷小代换.
对于代数和中各无穷小不能分别替换.
例2 求 lim tan x sin x . x0 sin3 2 x
错解 当x 0时, tan x ~ x, sin x ~ x.
左极限 : (1) lim x x0
f (x)
f
( x0
0)
(2) lim f (x) x-
右极限 : (1) lim x x0
f
(x)
f
( x0
0)
(2) lim f (x) x
极限存在的充要条件：左极限=右极限
lim
xx0
f
(x)
A
f
(x0
0)
f
(x0
0)
A
lim f (x) A lim f (x) lim f (x) A
原式 lim x x 0.
x0 (2 x)3
解 当x 0时, sin 2x ~ 2x,
tan x sin x tan x(1 cos x) ~ 1 x3 ,
原式 lim
1 x3 2
1
.
2
x0 (2 x)3 16
求极限方法小结
1、初等数学技巧计算：
通分，根式有理化，变量代替，提出公因子，抓“大头”
n n2 1 n2 2
n2 n
解
n n2 n
1 n2 1
1 n2 n
n ,
n2 1
又 lim n
n lim n2 n n
1 1 1 1,
n
n
1
lim
n
lim n2 1 n
1,11 n2 Nhomakorabea由夹逼定理得
lim( 1 1 1 ) 1.
n n2 1 n2 2
n2 n
（3）无穷小量比较
常用等价无穷小: 当x 0时,
sin x ~ x,
arcsin x ~ x,
tan x ~ x,
arctan x ~ x,
ln(1 x) ~ x, e x 1 ~ x,
1 cos x ~ 1 x2 , 2
ax
1 ~ x ln a,
(1
1
x)n
1~ 1 x.
n
(1 x)a 1 ~ ax
).
解 n 时,是无穷小之和． 先变形再求极限.
1
lim(
n
n
2
2 n2
n n2
)
lim 1
n
2 n2
n
1
n(n 1)
lim 2 n
n2
1 lim (1 n 2
1) n
1. 2
例2
求
lim
x
2x3 7x3
3x2 4x2
5 1
.
解
x
时,
分子,
分母的极限都是无穷大
.(
型
)
先用x 3去除分子分母 , 分出无穷小, 再求极限 .
x
x
x
小结：求极限时需讨论左右的情况：
①分段函数(绝对值函数)在分段点的极限；
②在求含au , eu ,arctan u等项的函数在u 时 的极限时要注意分别考虑u , u .
1
例如在判断lim e x的存在性时就需要分开讨论. x0
y=f(x)在点x0处连续
y=f(x)在点x0处有定义
y = f(x) 在 点 x0 处 极 限 存 在