函数极限与连续的MATLAB求解

实验课程： 数学分析 专业： 数学与应用数学 班级： 09级数本一班 学号： 2009403078 姓名： 王h实验一 函数极限（黑体三号）【实验目的】1.掌握使用Matlab 求极限的方法2.通过Matlab 实验理解掌握极限的定义。

【实验内容】1.求函数极限 2. 求数列极限 3. 了解函数在某点连续【实验所使用的仪器设备与软件平台】实验使用MATLAB 软件【实验方法与步骤】（阐述实验的原理、方案、方法及完成实验的具体步骤等，对于必须编写计算机程序的实验，要附上编写的程序）一、 实验原理：1.运用数列极限的定义。

2.函数极限的定义。

3.函数)(x f 在0x 点连续的定义。

4.运用极限)(limx f 与)(lim x f 存在的充要条件。

二、 实验方案与方法：首先了解极限的定义，然后运用Matlab 软件编写程序求极限。

在使用Matlab 时要会运用声明符号变量syms,并且针对函数求极限的情况（左极限或右极限以及趋近于某点的左右极限等不同情况）编写相应的程序。

三、 实验步骤： 1. 先确定函数极限求∞→n limnn，)1ln(cos 1lim+-→x e x xx ，22)2(sin ln lim x x x -→ππ，xx arctan lim ∞→，xx xx 2)1(lim +∞→2. 以第一个为例编写程序如下：3.再求数列极限618.0215lim1≈-=+∞→n n n F F （其中已知数列])251()251[(51F 11++--+=n n n【实验结果】【结果分析与讨论】。

matlab计算函数极值,如何⽤MATLAB求函数的极值点和最⼤值两种⽅法：1、求导的⽅法：syms x y；>>y=x^3+x^2+1>>diff(y)ans =3*x^2 + 2*x>>solve(ans)ans=-2/3极值有两点。

同时也是最值；2、直接⽤最⼩值函数：求最⼤值，既求-y的最⼩值：>>f=@(x)(-x^3-x^2-1)f =@(x)(-x^3-x^2-1)>>x=fminunc(f,-3,3)%在-3；-3范围内找Warning: Gradient must be provided fortrust-region method; using line-search methodinstead. > In fminunc at354Optimization terminated: relative infinity-norm of gradient lessthan options.TolFun.x =-0.6667>> f(x)ans =-1.1481在规定范围内的最⼤值是1.1481由于函数的局限性，求出的极值可能是局部最⼩(⼤)值。

求全局最值要⽤遗传算法。

例⼦：syms xf=(200+5*x)*(0.65-x*0.01)-x*0.45;s=diff(f);%⼀阶导数s2=diff(f,2);%⼆阶导数h=double(solve(s));%⼀阶导数为零的点可能就是极值点，注意是可能，详情请见⾼数课本fori=1:length(h)ifsubs(s2,x,h(i))<0disp(['函数在' num2str(h(i))'处取得极⼤值，极⼤值为' num2str(subs(f,x,h(i)))])elseifsubs(s2,x,h(i))>0disp(['函数在' num2str(h(i))'处取得极⼩值，极⼩值为'num2str(subs(f,x,h(i)))])elsedisp(['函数在' num2str(h(i))'处⼆阶导数也为0，故在该点处函数可能有极⼤值、极⼩值或⽆极值'])%%%详情见⾼数课本endend。

matlab求曲线极值程序,matlab函数求极值matlab函数求极值.pptmatlab函数求极值matlab函数求极值* * 函数的极值 1、⼀元函数的极值 函数命令：fminbnd 调⽤格式：[x,feval,exitflag,output]=fminbnd(fun,x1,x2,options) %求fun在区间(x1,x2)上的极值. 返回值： x:函数fun在(x1,x2)内的极值点 feval:求得函数的极值 exitflag: exitflag>0,函数收敛于解x处 exitflag=0,已达最⼤迭代次数 exiflag<0,函数在计算区间内不收敛. 例1：求函数 在 上的极⼩值. fun=inline('(x+pi)*exp(abs(sin(x+pi)))')[x,feval,exitflag,output]=fminbnd(fun,-pi/2,pi/2) fun = Inline function: fun(x) = (x+pi)*exp(abs(sin(x+pi))) x = -1.2999e-005 feval = 3.1416 exitflag = 1 output = iterations: 21 funcCount: 22 algorithm: 'golden section search, parabolic interpolation' message: [1x112 char] xx=-pi/2:pi/200:pi/2; yxx=(xx+pi).*exp(abs(sin(xx+pi))); plot(xx,yxx) xlabel('x'),grid on % 可以⽤命令[xx,yy]=ginput(1) 从局部图上取出极值点及相应函数值 例2：求解函数humps的极⼩值. type humps %humps 是⼀个Matlab提供的M 函数⽂件 function [out1,out2] = humps(x) %HUMPS A function used by QUADDEMO, ZERODEMO and FPLOTDEMO. % Y = HUMPS(X) is a function with strong maxima near x = .3 % and x = .9. % % [X,Y] = HUMPS(X) also returns X. With no input arguments, % HUMPS uses X = 0:.05:1. % % Example: % plot(humps) % % See QUADDEMO, ZERODEMO and FPLOTDEMO. % Copyright 1984-2002 The MathWorks, Inc. % $Revision: 5.8 $ $Date: 2002/04/15 03:34:07 $ if nargin==0, x = 0:.05:1; end y = 1 ./ ((x-.3).^2 + .01) + 1 ./ ((x-.9).^2 + .04) - 6; if nargout==2, out1 = x; out2 = y; else out1 = y; end[x,y]=fminbnd(@humps,0.5,0.8) x = 0.6370 y = 11.2528 xx=0:0.001:2; yy=humps(xx); plot(xx,yy) 例3：求 在(0,1)内的极⼩值. type myfunmin1 %显⽰M⽂件内容 function f=myfunmin1(x) f=x.^x; [x,y]=fminbnd(@myfunmin1,0,1) x = 0.3679 y =0.6922 xx=0:0.001:1; yy=myfunmin1(xx); plot(xx,yy) [x,y]=fminbnd('x.^x',0,1) x = 0.3679 y = 0.6922 2、 多元函数的极值 函数命令：fminsearch 调⽤格式：[x,feval,exitflag,output]=fminsearch(fun,x0,optipons) % 求在x0附近的极值 例4：求 的极⼩值. type myfunmin2 function f=myfunmin2(v) x=v(1); y=v(2); f=100*(y-x.^2).^2+(1-x).^2;[sx,sfeval]=fminsearch(@myfunmin2,[1 1]) sx。

实验三 用matlab 求极限和导数1.求极限、导数的MATLAB 命令MATLAB 中主要用limit,diff 分别求函数的极限与导数。

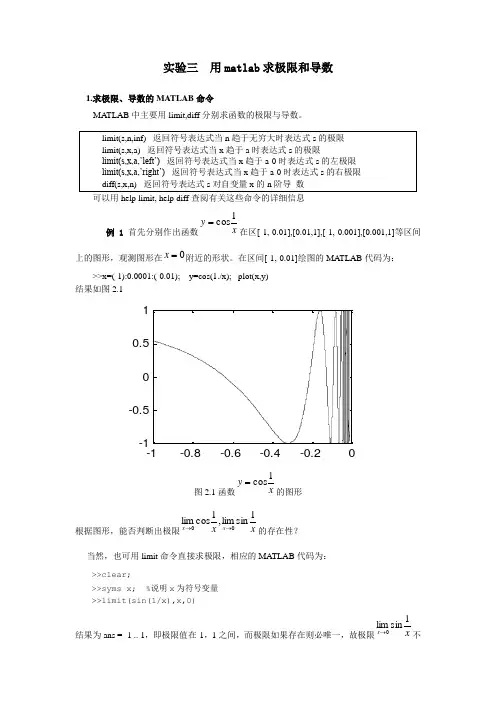
可以用help limit, help diff 查阅有关这些命令的详细信息例1首先分别作出函数x y 1cos=在区[-1,-0.01],[0.01,1],[-1,-0.001],[0.001,1]等区间上的图形，观测图形在0=x 附近的形状。

在区间[-1,-0.01]绘图的MA TLAB 代码为： >>x=(-1):0.0001:(-0.01); y=cos(1./x); plot(x,y) 结果如图2.1图2.1函数x y 1cos=的图形根据图形，能否判断出极限x x x x 1sinlim ,1cos lim 00→→的存在性？ 当然，也可用limit 命令直接求极限，相应的MATLAB 代码为：>>clear;>>syms x; %说明x 为符号变量>>limit(sin(1/x),x,0)结果为ans = -1 .. 1，即极限值在-1，1之间，而极限如果存在则必唯一，故极限x x 1sinlim 0→不存在，同样，极限x x 1coslim 0→也不存在。

例2 首先分别作出函数x xy sin =在区间[-1,-0.01],[0.01,1],[-1,-0.001],[0.001,1]等区间上的图形，观测图形在0=x 附近的形状。

在区间[-1,-0.01]绘图的MA TLAB 代码为： >>x=(-1):0.0001:(-0.01); y=sin(x)./x; plot(x,y) 结果如图2.2图2.2 函数x xy sin =的图形根据图形，能否判断出极限1sin lim0=→x xx 的正确性？当然，也可用limit 命令直接求极限，相应的MATLAB 代码为：>>clear; >>syms x;>>limit(sin(x)/x,x,0) 结果为ans =1.例3 观测当n 趋于无穷大时，数列n n n a )11(+=和1)11(++=n n n A 的变化趋势。

文章主题：深入探讨MATLAB中的多项式运算及求极限、复杂函数求极限MATLAB（Matrix Laboratory）是一款强大的数学软件，广泛应用于工程、科学、经济等领域。

在MATLAB中，多项式运算及求极限、复杂函数求极限是常见且重要的数学问题，对于提高数学建模和计算能力具有重要意义。

本文将从简到繁地探讨MATLAB中的多项式运算及求极限、复杂函数求极限，以帮助读者深入理解这一主题。

一、MATLAB中的多项式运算多项式是数学中常见的代数表达式，通常以系数的形式表示。

在MATLAB中，可以使用多种方法进行多项式的运算，如加法、减法、乘法、除法等。

对于两个多项式f(x)和g(x)，可以使用“+”、“-”、“*”、“/”等运算符进行运算。

在实际应用中，多项式的运算往往涉及到多项式系数的提取、多项式的乘方、多项式的符号变化等操作。

MATLAB提供了丰富的函数和工具箱，如polyval、polyfit、roots等，可以帮助用户进行多项式的运算。

通过这些工具，用户可以方便地进行多项式的求值、拟合、求根等操作。

二、MATLAB中的多项式求极限求多项式的极限是微积分中常见的问题，对于研究函数的性质和图像具有重要意义。

在MATLAB中，可以通过lim函数来求多项式的极限。

lim函数可以接受不同的输入参数，如函数、变量、极限点等，从而计算多项式在某一点的极限值。

在进行多项式求极限时，需要注意的是对极限的性质和运算规则。

MATLAB中的lim函数遵循了标准的极限计算规则，如极限的四则运算法则、极限的有界性、极限的夹逼定理等。

用户可以通过lim函数灵活地进行多项式求极限的计算和分析。

三、MATLAB中的复杂函数求极限除了多项式，复杂函数在工程和科学中也具有广泛的应用。

MATLAB提供了丰富的函数和工具箱，如syms、limit、diff等，可以帮助用户进行复杂函数的求导、求极限等操作。

对于复杂函数的极限计算，需要综合运用代数运算、微分计算、极限性质等技巧。

matlab计算函数极限标题：用MATLAB计算函数极限在数学中，极限是研究函数在某个特定点附近的行为的重要概念之一。

计算函数的极限有助于我们了解函数在该点附近的性质，包括函数的趋势、连续性以及导数等。

在本文中，我们将使用MATLAB 来计算函数的极限，并通过实例来说明这一过程。

在MATLAB中，我们可以使用`limit`函数来计算函数的极限。

`limit`函数的语法为：```L = limit(f, x, a)```其中，`f`是输入的函数表达式，`x`是自变量，`a`是自变量趋于的点。

`limit`函数将返回函数在自变量趋于该点时的极限值`L`。

下面，我们通过一个具体的例子来演示如何使用MATLAB计算函数的极限。

假设我们要计算函数`f(x) = (x^2 - 1)/(x - 1)`在`x`趋于1时的极限。

我们定义函数`f`：```matlabsyms x;f = (x^2 - 1)/(x - 1);```然后，我们使用`limit`函数计算极限：```matlabL = limit(f, x, 1);```运行以上代码后，MATLAB将返回极限值`L`。

除了计算函数在某个点处的极限外，MATLAB还可以计算函数在正无穷或负无穷处的极限。

例如，我们要计算函数`g(x) = 1/x^2`在`x`趋于正无穷时的极限，可以使用以下代码：```matlabsyms x;g = 1/x^2;L = limit(g, x, inf);```同样地，MATLAB将返回极限值`L`。

除了计算极限值外，MATLAB还可以判断函数在某个点是否存在极限。

如果函数在某个点处的左极限和右极限相等，则称该函数在该点处存在极限。

我们可以使用`islimit`函数来判断函数在某个点是否存在极限。

例如，我们要判断函数`h(x) = sin(x)/x`在`x`趋于0时是否存在极限，可以使用以下代码：```matlabsyms x;h = sin(x)/x;exist_limit = islimit(h, x, 0);```运行以上代码后，MATLAB将返回布尔值`exist_limit`，若为`true`则表示函数在该点处存在极限，若为`false`则表示不存在。

Matlab 求极限网上有许多关于使用Matlab 求极限的文章，我粗略浏览了一下发现都只是简单介绍了求极限函数limit 的一种应用情况，大多就是只针对求双向极限进行了介绍，但是有的情况只要求左极限或则右极限，还有的是求趋于无穷的极限，这借个方面都很少有文章介绍，所以这里系统的介绍一下关于使用Matlab 求极限的一系列问题。

极限无外乎7种未定式，在手工求解时常用方法是洛必达法则、等价无穷小法和泰勒公式法。

这三种方法中洛必达法则并不是所有的极限都可以求的，其要求分子分母都可导，并且导函数的极限存在，所以对于分子分母不可导或者可导，但是导函数极限不存在的情况就不能用洛必达法则，而等价无穷小法其实就是泰勒公式的简化版，忽略了高次项而已。

手工求极限必须遵守的一个规则就是“先化简”，对于一些复杂表达式的极限手工求解化简不恰单时是很难求出的，或则容易求错的，都是借助Matlab 就可以很轻松的求解复杂极限。

一、求x 0处的极限（双向极限）求一个表达式f (x )在自变量x 趋于某一点x 0时的极限，0lim ()x x f x 使用的Matlab 函数是limit 函数，这时的调用格式是：limit(fun,var,x 0)其中fun 是所要求极限的表达，var 是自变量，x 0是自变量趋于的点例：求sin(x )/x 在x 趋于0时的极限解：运行以后得到结果：二、求趋于x 0-的极限（左极限）求一个表达式f (x )在自变量x 趋于某一点x 0-时的极限，0lim ()x x f x -→ 这时limit 函数的调用格式是：limit(fun,var,x 0,’left’)其中fun 是所要求极限的表达，var 是自变量，x 0是自变量趋于的点，left 代表是趋于x 0的左边例：求表达式1/x 的左极限，x 趋于0-解：运行以后得到结果：可以看到当x 趋于0-时，1/x 的值是-∞.三、求x 趋于x 0+的极限（右极限）求一个表达式f (x )在自变量x 趋于某一点x 0-时的极限，0lim ()x x f x +→ 这时limit 函数的调用格式是：limit(fun,var,x 0,’right’)其中fun 是所要求极限的表达，var 是自变量，x 0是自变量趋于的点，right 代表是趋于x 0的右边例：求表达式1/x 的右极限，x 趋于0+解：运行以后得到结果：可以看到当x 趋于0+时，1/x 的值是+∞.四、求x →∞时的极限当然这里的∞也包括-∞和+∞，正负的求解方法同二、三中一样。

第六章：函数，极限与连续的MATLAB1 映射与函数。

（1）集合（更多的是用于数组间的运算）：ismember（一个个元素判断是否是子集，返回一个数组）；intersect（求交集，返回结果数组）；setdiff(a,b)（求差集，属于a不属于b的数组）；union （求并集）。

（2）函数：定义方法：y=@(x)f(x)；syms x y=f(x)；y=sym(‘f(x)’);求反函数：finverse(f,t)；求复合函数f(g(x))：y=compose(f,g)；2 求极限。

（1）求数列极限：limit(xn, n, inf)；limit(xn, inf)。

（2）求函数极限：limit(fx, x, x0(, ‘left’) )；limit(fx, x, inf)。

3 函数的连续性与间断点。

（1）判断连续性的函数代码：P144。

（2）判断x0是否是函数f(x)的间断点的函数代码：（P146，文件夹MATLAB学习中的程序储存里）。

实际应用中，可以根据绘图来判定是否是间断点。

（3）求函数区间的方法：P215。

第七章：导数与微分的MATLAB求解1 导数求解：diff(fx,x,n)后面2个可以省略，则是求导函数；隐函数的导数求解见P156的2个例子；稍微总结就是把y定义为y=sym(‘y(x)’)，然后定义隐函数的表达式为F=…，把表达式等号右侧置为0，左侧为F函数表达式，之后：diff(F,x)。

参数方程确定的函数的导数P157。

2 洛必达法则：P168.3 泰勒公式：P172.另外，MATLAB有taylor(fx,x,n,a)。

MATLAB提供了泰勒级数逼近分析界面：taylortool，4 函数的凹凸性与曲线的单调性：求函数单调区间及各个区间单调性的判定：P175。

求凹凸性与拐点的程序：P179。

求方程实根从而可以进行一些特殊数值表达式的求解（比如（-8）^(1/3)的求解）的函数代码：P176。

一元函数微分学实验1 一元函数的图形（基础实验）实验目的 通过图形加深对函数及其性质的认识与理解, 掌握运用函数的图形来观察和分析 函数的有关特性与变化趋势的方法,建立数形结合的思想; 掌握用Matlab 作平面曲线图性的方法与技巧.初等函数的图形2 作出函数x y tan =和x y cot =的图形观察其周期性和变化趋势. 解：程序代码：>> x=linspace(0,2*pi,600); t=sin(x)./(cos(x)+eps);plot(x,t);title('tan(x)');axis ([0,2*pi,-50,50]); 图象：程序代码：>> x=linspace(0,2*pi,100); ct=cos(x)./(sin(x)+eps);plot(x,ct);title('cot(x)');axis ([0,2*pi,-50,50]); 图象：4在区间]1,1[-画出函数xy 1sin =的图形.解：程序代码：>> x=linspace(-1,1,10000);y=sin(1./x); plot(x,y);axis([-1,1,-2,2]) 图象：二维参数方程作图6画出参数方程⎩⎨⎧==t t t y tt t x 3cos sin )(5cos cos )(的图形：解：程序代码：>> t=linspace(0,2*pi,100);plot(cos(t).*cos(5*t),sin(t).*cos(3*t)); 图象：极坐标方程作图8 作出极坐标方程为10/t e r =的对数螺线的图形. 解：程序代码：>> t=0:0.01:2*pi; r=exp(t/10);polar(log(t+eps),log(r+eps)); 图象：90270分段函数作图10 作出符号函数x y sgn =的图形. 解：>> x=linspace(-100,100,10000); y=sign(x); plot(x,y);axis([-100 100 -2 2]);函数性质的研究12研究函数)3(log 3)(35x e x x f x -++=在区间]2,2[-上图形的特征.解：程序代码：>> x=linspace(-2,2,10000);y=x.^5+3*exp(x)+log(3-x)/log(3); plot(x,y); 图象：实验2 极限与连续（基础实验）实验目的 通过计算与作图, 从直观上揭示极限的本质,加深对极限概念的理解. 掌握用 Matlab 画散点图, 以及计算极限的方法. 深入理解函数连续的概念,熟悉几种间断点的图形 特征,理解闭区间上连续函数的几个重要性质.作散点图14分别画出坐标为)10,,2,1(),4,(),,(3222 =+i i i i i i 的散点图, 并画出折线图. 解：散点图程序代码：plot(i,i.^2,'.')或：>> x=1:10;y=x.^2;for i=1:10;plot(x(i),y(i),'r')hold onend折线图程序代码：>> i=1:10;plot(i,i.^2,'-x')程序代码： >> i=1:10;plot(i.^2,4*(i.^2)+i.^3,'.')>> i=1:10;plot(i.^2,4*(i.^2)+i.^3,'-x')数列极限的概念16通过动画观察当∞→n 时数列21n a n =的变化趋势.解：程序代码： >> n=1:100; an=(n.^2); n=1:100; an=1./(n.^2); n=1:100; an=1./(n.^2); for i=1:100plot(n(1:i),an(1:i)),axis([0,100,0,1]) pause(0.1) end 图象：函数的极限18在区间]4,4[-上作出函数xx xx x f --=339)(的图形, 并研究 )(lim x f x ∞→ 和 ).(lim 1x f x →解：作出函数x x xx x f --=339)(在区间]4,4[-上的图形>> x=-4:0.01:4;y=(x.^3-9*x)./(x.^3-x+eps); plot(x,y)16从图上看，()f x 在x →1与x →∞时极限为0两个重要极限 20计算极限⎪⎭⎫⎝⎛+→x x x x x sin 11sin lim )1(0 x x e x 2lim )2(+∞→30sin tan lim )3(xx x x -→ x x x 0lim )4(+→ x xx ln cot ln lim )5(0+→ x x x ln lim )6(20+→ x x xx x x sin cos sin lim )7(20-→ 125523lim )8(323+++-∞→x x x x x xx x e e x x x sin 2lim )9(0----→ xx x x cos 110sin lim )10(-→⎪⎭⎫ ⎝⎛ 解：（1）>> limit(x*sin(1/x)+1/x*sin(x))ans =1(2) >> limit(x^2/exp(x),inf) ans = 0(3) >> limit((tan(x)-sin(8))/x^3) ans =NaN(4) >> limit(x^x,x,0,'right') ans =1(5) >> limit(log(cot(x))/log(x),x,0,'right') ans =-1(6) >> limit(x^2*log(x),x,0,'right') ans =0(7) >> limit((sin(x)-x.*cos(x))./(x.^2.*sin(x)),x,0) ans =1/3(8) >> limit((3*x.^3-2*x.^2+5)/(5*x.^3+2*+1),x,inf) ans =3/5(9) >> limit((exp(x)-exp(-x)-2*x)./(x-sin(x))) ans =2(10) >> limit((sin(x)/x).^(1/(1-cos(x)))) ans =exp(-1/3)实验3 导数（基础实验）实验目的 深入理解导数与微分的概念, 导数的几何意义. 掌握用Matlab 求导数与高 阶导数的方法. 深入理解和掌握求隐函数的导数, 以及求由参数方程定义的函数的导数的方法. 导数概念与导数的几何意义22作函数71232)(23+-+=x x x x f 的图形和在1-=x 处的切线. 解：作函数71232)(23+-+=x x x x f 的图形程序代码： >> syms x;>> y=2*x^3+3*x^2-12*x+7; >> diff(y) ans =6*x^2+6*x-12 >> syms x;y=2*x^3+3*x^2-12*x+7; >> f=diff(y) f =6*x^2+6*x-12 >> x=-1;f1=6*x^2+6*x-12 f1 = -12>> f2=2*x^3+3*x^2-12*x+7 f2 = 20>> x=linspace(-10,10,1000);y1=2*x.^3+3*x.^2-12*x+7; y2=-12*(x+1)+20; plot(x,y1,'r',x,y2,'g')求函数的导数与微分24求函数bx ax x f cos sin )(=的一阶导数. 并求.1⎪⎭⎫⎝⎛+'b a f解：求函数bx ax x f cos sin )(=的一阶导数程序代码： >> syms a b x y;y= sin(a*x)*cos(b*x); D1=diff(y,x,1) 答案：D1 =cos(a*x)*a*cos(b*x)-sin(a*x)*sin(b*x)*b求.1⎪⎭⎫ ⎝⎛+'b a f程序代码： >> x=1/(a+b);>> cos(a*x)*a*cos(b*x)-sin(a*x)*sin(b*x)*b答案：ans =cos(a/(a+b))*a*cos(b/(a+b))-sin(a/(a+b))*sin(b/(a+b))*b 拉格朗日中值定理26对函数),2)(1()(--=x x x x f 观察罗尔定理的几何意义. (1) 画出)(x f y =与)(x f '的图形, 并求出1x 与.2x 解：程序代码：>> syms x;f=x*(x-1)*(x-2); f1=diff(f) f1 =(x-1)*(x-2)+x*(x-2)+x*(x-1) >> solve(f1) ans =1+1/3*3^(1/2) 1-1/3*3^(1/2)>> x=linspace(-10,10,1000); y1=x.*(x-1).*(x-2);y2 =(x-1).*(x-2)+x.*(x-2)+x.*(x-1); plot(x,y1,x,y2)(2)画出)(x f y =及其在点))(,(11x f x 与))(,(22x f x 处的切线. 程序代码：>> syms x; >> f=x*(x-1)*(x-2); >> f1=diff(f) f1 =(x-1)*(x-2)+x*(x-2)+x*(x-1) >> solve(f1) ans =1+1/3*3^(1/2) 1-1/3*3^(1/2)>> x=linspace(-3,3,1000); >> y1=x.*(x-1).*(x-2);>> y2 =(x-1).*(x-2)+x.*(x-2)+x.*(x-1); >> plot(x,y1,x,y2) >> hold on>> x=1+1/3*3^(1/2); >> yx1=x*(x-1)*(x-2) yx1 =-0.3849>> x=1-1/3*3^(1/2); >> yx2=x*(x-1)*(x-2) yx2 =0.3849x=linspace(-3,3,1000); yx1 =-0.3849*x.^0; yx2 =0.3849*x.^0; plot(x,yx1,x,yx2)28求下列函数的导数:(1) 31+=x e y ; 解：程序代码：>> syms x y; y=exp((x+1)^3); D1=diff(y,1) 答案：D1 =3*(x+1)^2*exp((x+1)^3)(2) )]42ln[tan(π+=x y ;解：程序代码：>> syms x;y=log(tan(x/2+pi/4)); D1=diff(y,1) 答案：D1 =(1/2+1/2*tan(1/2*x+1/4*pi)^2)/tan(1/2*x+1/4*pi)(3) x x y sin ln cot 212+=;解：程序代码：>> syms x;y=1/2*(cot(x))^2+log(sin(x)); D1=diff(y,1) 答案：D1 =cot(x)*(-1-cot(x)^2)+cos(x)/sin(x) (4) xy 2arctan21=. 解：程序代码：>> syms x;>> y=sqrt(2)*atan(sqrt(2)/x); >> D1=diff(y,1) 答案：D1 =-2/x^2/(1+2/x^2)一元函数积分学与空间图形的画法实验4 一元函数积分学(基础实验)实验目的 掌握用Matlab 计算不定积分与定积分的方法. 通过作图和观察, 深入理解定积分的概念和思想方法. 初步了解定积分的近似计算方法. 理解变上限积分的概念. 提高应用 定积分解决各种问题的能力.不定积分计算30求.)1(532⎰-dx x x解：程序代码：>> syms x y;>> y=x^2*(1-x^3)^5; >> R=int(y,x) 答案：R =-1/18*x^18+1/3*x^15-5/6*x^12+10/9*x^9-5/6*x^6+1/3*x^332求.arctan 2⎰xdx x解：程序代码：>> syms x y;>> y=x^2*atan(x); >> R=int(y,x) 答案：R =1/3*x^3*atan(x)-1/6*x^2+1/6*log(x^2+1)定积分计算34 求.)(102⎰-dx x x解：程序代码：>> syms x y; >> y=x-x^2;>> R=int(y,x,0,1) 答案： R =1/6变上限积分36 画出变上限函数⎰x dt t t 02sin 及其导函数的图形.解：程序代码：>> syms x y t; >> y=t*sin(t^2); >> R=int(y,x,0,x) 答案：R =t*sin(t^2)*x 再求导函数 程序代码：>> DR=diff(R,x,1) 答案：DR =t*sin(t^2)实验5 空间图形的画法(基础实验)实验目的 掌握用Matlab 绘制空间曲面和曲线的方法. 熟悉常用空间曲线和空间曲面 的图形特征,通过作图和观察, 提高空间想像能力. 深入理解二次曲面方程及其图形.一般二元函数作图38作出函数2214y x z ++=的图形.解：程序代码：>> x=linspace(-5,5,500); [x,y]=meshgrid(x); z=4./(1+x.^2+y.^2); mesh(x,y,z);xlabel('x-axis'),ylabel('y-axis'),zlabel('z-axis');title('function')40作出函数)94cos(22y x z +=的图形. 解：程序代码：>> x=-10:0.1:10;[x,y]=meshgrid(x);z=cos(4*x.^2+9*y.^2); mesh(x,y,z);xlabel('x-axis'),ylabel('y-axis'),zlabel('z-axis');title('function')讨论：坐标轴选取范围不同时，图形差异很大，对本题尤为明显，如右图为坐标轴[-1，1]二次曲面42作出单叶双曲面1941222=-+z y x 的图形.(曲面的参数方程为 ,tan 3,cos sec 2,sin sec u z v u y v u x === (.20,2/2/πππ≤≤<<-v u ))解：程序代码：>> v=0:pi/100:2*pi; >> u=-pi/2:pi/100:pi/2; >> [U,V]=meshgrid(u,v); >> x=sec(U).*sin(V); >> y=2*sec(U).*cos(V); >> z=3*tan(U); >> surf(x,y,z)44 可以证明: 函数xy z =的图形是双曲抛物面. 在区域22,22≤≤-≤≤-y x 上作出它的图形.解：程序代码：>> x=-2:0.01:2;[x,y]=meshgrid(x); >> z=x.*y;>> mesh(x,y,z);46 画出参数曲面]2,001.0[],4,0[)5/2/ln(tan cos sin sin sin cos ∈∈⎪⎩⎪⎨⎧++===v u u v v z vu y v u x π 的图形.解：程序代码：>> v=0.001:0.001:2; >> u=0:pi/100:4*pi;>> [U,V]=meshgrid(u,v); >> x=cos(U).*sin(V); >> y=sin(U).*sin(V);>> z=cos(V)+log(tan(V/2)+U/5); >> mesh(x,y,z);空间曲线48 作出空间曲线)60(2,sin ,cos π≤≤===t t z t t y t t x 的图形. 解：程序代码：>> syms t;ezplot3(t*cos(t),t*sin(t),2*t,[0,6*pi])xx = t cos(t), y = t sin(t), z = 2 tz50绘制参数曲线 ⎪⎪⎩⎪⎪⎨⎧=+==t z t y t x arctan 211cos 2的图形.解：程序代码：>> t=-2*pi:pi/100:2*pi;x=cos(t).*cos(t);y=1./(1+2*t);z=atan(t); plot3(x,y,z);grid;xlabel('x'),ylabel('y'),zlabel('z')xyz多元函数微积分实验6 多元函数微分学（基础实验）实验目的 掌握利用Matlab 计算多元函数偏导数和全微分的方法, 掌握计算二元函数极值和条件极值的方法. 理解和掌握曲面的切平面的作法. 通过作图和观察, 理解二元 函数的性质、方向导数、梯度和等高线的概念.求多元函数的偏导数与全微分 52设),(cos )sin(2xy xy z +=求.,,,222yx z x z y z x z ∂∂∂∂∂∂∂∂∂ 解：程序代码：>> syms x y;S=sin(x*y)+(cos(x*y))^2; D1=diff(S,'x',1); D2=diff(S,'y',1); D3=diff(S,'x',2); D4=diff(S,'y',2); D1,D2,D3,D4答案： D1 = cos(x*y)*y-2*cos(x*y)*sin(x*y)*yD2 = cos(x*y)*x-2*cos(x*y)*sin(x*y)*xD3 =-sin(x*y)*y^2+2*sin(x*y)^2*y^2-2*cos(x*y)^2*y^2 D4 = -sin(x*y)*x^2+2*sin(x*y)^2*x^2-2*cos(x*y)^2*x^2实验7 多元函数积分学（基础实验）实验目的掌握用Matlab 计算二重积分与三重积分的方法; 深入理解曲线积分、曲面积分的 概念和计算方法. 提高应用重积分和曲线、曲面积分解决各种问题的能力.计算重积分54计算,2dxdy xy D⎰⎰其中D 为由,,2y x y x ==+ 2=y 所围成的有界区域.解：程序代码：>> syms x y;int(int(x*y^2,x,2-y,sqrt(y)),y,1,2) 答案：ans =193/120 重积分的应用56求旋转抛物面224y x z --=在Oxy 平面上部的面积.S 解：程序代码：>> int(2*pi*r,r,0,2) 答案： ans =4*pi无穷级数与微分方程实验8 无穷级数（基础实验） 实验目的观察无穷级数部分和的变化趋势,进一步理解级数的审敛法以及幂级数部分和对函数的 逼近. 掌握用Matlab 求无穷级数的和, 求幂级数的收敛域, 展开函数为幂级数以及展开周期函数为傅里叶级数的方法.数项级数58(1)观察级数∑∞=12 1n n的部分和序列的变化趋势.解：程序代码：for i=1:100 s=0;for n=1:i s=s+1/n^2;endplot(i,s,'.');hold on;end(2) 观察级数∑∞=11n n的部分和序列的变化趋势.>> for i=1:100 s=0; for n=1:i s=s+1/n; endplot(i,s,'.'); hold on; end60 求∑∞=++123841n n n 的值. 解：程序代码：>> syms n;score=symsum(1/(4*n^2+8*n+3),1,inf) 答案： score =1/6函数的幂级数展开62求x arctan 的5阶泰勒展开式. >> syms x;>> T5=taylor(atan(x),6) 答案：T5 =x-1/3*x^3+1/5*x^5实验9 微分方程（基础实验）实验目的 理解常微分方程解的概念以及积分曲线和方向场的概念,掌握利用 Matlab 求微分方程及方程组解的常用命令和方法.求解微分方程64求微分方程 22x xe xy y -=+'的通解. 解：程序代码：>> y=dsolve('Dy+2*x*y=x*exp(-x^2)','x') 答案：y =(1/2*x^2+C1)*exp(-x^2)66求微分方程x e y y y x 2cos 52=+'-''的通解. 解：程序代码：>> y=dsolve('D2y-2*Dy+5*y=exp(x)*cos(2*x)','x') 答案： y =exp(x)*sin(2*x)*C2+exp(x)*cos(2*x)*C1+1/4*exp(x)*sin(2*x)*x68求微分方程组⎪⎪⎩⎪⎪⎨⎧=--=++02y x dtdy e y x dt dx t 在初始条件0,100====t t y x 下的特解.解：程序代码：>> [x,y]=dsolve('Dx+x+2*y-exp(t)','Dy-x-y','x(0)=1','y(0)=0','t') 答案： x = cos(t)y = 1/2*sin(t)-1/2*cos(t)+1/2*exp(t)70求解微分方程,)1(122/5+=+-x x y dx dy 并作出积分曲线. 解：程序代码：>> syms x yy=dsolve('Dy-2*y/(x+1)-(x+1)^(5/2)','x') 答案：y =(2/3*(x+1)^(3/2)+C1)*(x+1)^2 做积分曲线 由>> syms x yx=linspace(-5,5,100); C=input('请输入C 的值:'); y=(2/3*(x+1).^(3/2)+C).*(x+1).^2; plot(x,y)例如对应有： 请输入C 的值:2 请输入C 的值:20矩阵运算与方程组求解实验10 行列式与矩阵实验目的掌握矩阵的输入方法. 掌握利用Matlab 对矩阵进行转置、加、减、数乘、相乘、乘方等运算, 并能求矩阵的逆矩阵和计算方阵的行列式.矩阵A 的转置函数Transpose[A]72 求矩阵⎪⎪⎪⎪⎪⎭⎫⎝⎛411365243271的转置. 解：程序代码：>> A=[1,7,2;3,4,2;5,6,3;1,1,4]; >> Sove=A' 答案：Sove =1 3 5 1 7 4 6 12 234 矩阵线性运算 73设,291724,624543⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫⎝⎛=B A 求.24,A B B A -+ 解：程序代码：>> A=[3,4,5;4,2,6]; B=[4,2,7;1,9,2]; S1=A+B S2=4*B-2*A 答案：S1 =7 6 12 5 11 8 S2 =10 0 18 -4 32 -474设,148530291724,36242543⎪⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛=mb ma 求矩阵ma 与mb 的乘积. 解：程序代码：>> ma=[3,4,5,2;4,2,6,3];>> mb=[4,2,7;1,9,2;0,3,5;8,4,1]; >> Sove=ma*mb 答案：Sove =32 65 56 42 56 65 矩阵的乘法运算75设,101,530291724⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛=B A 求AB 与,A B T 并求.3A解：程序代码：>> A=[4 2 7;1 9 2;0 3 5]; B=[1;0;1]; >> AB=A*B AB = 11 3 5 >> BTA=B'*A BTA =4 5 12 >> A3=A^3 A3 =119 660 555 141 932 444 54 477 260 求方阵的逆 76 设,5123641033252312⎪⎪⎪⎪⎪⎭⎫⎝⎛=A 求.1-A 解：程序代码：>> A=[2,1,3,2;5,2,3,3;0,1,4,6;3,2,1,5];Y=inv(A)答案：Y =-1.7500 1.3125 0.5000 -0.6875 5.5000 -3.6250 -2.0000 2.3750 0.5000 -0.1250 0.0000 -0.1250 -1.2500 0.6875 0.5000 -0.3125 77 设,221331317230,5121435133124403⎪⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎪⎪⎭⎫⎝⎛=B A 求.1B A - 解：程序代码：>> A=[3 0 4 4 ;2 1 3 3 ;1 5 3 4;1 2 1 5]; B=[0 3 2 ;7 1 3;1 3 3 ;1 2 2]; Solve=A'*B 答案：Solve =16 16 17 14 20 22 25 26 28 30 37 3978 解方程组⎪⎩⎪⎨⎧-=-+=+-=++.2442,63,723z y x z y x z y x解：程序代码：>> A=[3 2 1;1 -1 3;2 4 -4]; b=[7 6 -2]; >> A\b' 答案：ans =1.0000 1.00002.0000 求方阵的行列式79 求行列式 .3351110243152113------=D解：程序代码：>> A=[3,1,-1,2;-5,1,3,-4;2,0,1,-1;1,-5,3,-3]; D=det(A) 答案：D =4080求.11111111111122222222ddd d c c c c b b b b a a a a D ++++=解：程序代码：>> syms a b c d;D=[a^2+1/a^2 a 1/a 1;b^2+1/b^2 b 1/b 1;c^2+1/c^2 c 1/c 1;d^2+1/d^2 d 1/d 1]; det(D) 答案：ans =-(-c*d^2*b^3+c^2*d*b^3-c^3*d^2*a+c^3*d*a^2*b^4+c*d^2*a^3-c^3*d^2*a*b^4-c^2*d*a^3-c*d^2*b^3*a^4+c^2*d*b^3*a^4+c^3*d^2*b*a^4-c^3*d*b^2*a^4-c^2*d^3*b*a^4+c*d^3*b^2*a^4+c*d ^2*a^3*b^4-c^2*d*a^3*b^4+c^3*d^2*b-c^3*d*b^2-c^2*d^3*b+c*d^3*b^2+c^3*d*a^2+c^2*d^3*a-c *d^3*a^2-b*d^2*a^3+b^2*d*a^3+b^3*d^2*a-b^3*d*a^2-b^2*d^3*a+b*d^3*a^2+b*c^2*a^3-b^2*c*a ^3-b^3*c^2*a+b^3*c*a^2+b^2*c^3*a-b*c^3*a^2+c^2*d^3*a*b^4-c*d^3*a^2*b^4-b*d^2*a^3*c^4+b ^2*d*a^3*c^4+b^3*d^2*a*c^4-b^3*d*a^2*c^4-b^2*d^3*a*c^4+b*d^3*a^2*c^4+b*c^2*a^3*d^4-b^2*c*a^3*d^4-b^3*c^2*a*d^4+b^3*c*a^2*d^4+b^2*c^3*a*d^4-b*c^3*a^2*d^4)/a^2/c^2/d^2/b^281 计算范德蒙行列式.1111145444342413534333231252423222154321x x x x x x x x x x x x x x x x x x x x 解：程序代码：>> syms x1 x2 x3 x4 x5;>> A=[1,1,1,1,1;x1,x2,x3,x4,x5;x1^2,x2^2,x3^2,x4^2,x5^2; x1^3,x2^3,x3^3,x4^3,x5^3;x1^4,x2^4,x3^4,x4^4,x5^4];>> DC=det(A);>> DS=simple(DC) 答案：DS =(-x5+x4)*(x3-x5)*(x3-x4)*(-x5+x2)*(x2-x4)*(x2-x3)*(-x5+x1)*(x1-x4)*(x1-x3)*(x1-x2) 82 设矩阵 ,60975738723965110249746273⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----=A 求.),(|,|3A A tr A 解：程序代码：>> A=[3,7,2,6,-4;7,9,4,2,0;11,5,-6,9,3;2,7,-8,3,7;5,7,9,0,-6]; >> D=det(A),T=trace(A),A3=A^3 答案：D =11592 T = 3 A3=726 2062 944 294 -358 1848 3150 26 1516 228 1713 2218 31 1006 404 1743 984 -451 1222 384 801 2666 477 745 -125 向量的内积83 求向量}3,2,1{=u 与}0,1,1{-=v 的内积. 解：程序代码：>> u=[1 2 3]; v=[1 -1 0]; solve=dot(u,v) 答案：solve =-184设,001001⎪⎪⎪⎭⎫ ⎝⎛=λλλA 求.10A 一般地?=k A (k 是正整数).解：程序代码：>> syms r;>> A=[r,1,0;0,r,1;0,0,r]; >> A^10 答案：ans =[ r^10, 10*r^9, 45*r^8] [ 0, r^10, 10*r^9] [ 0, 0, r^10]85.求⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+++++a a a aa1111111111111111111111111的逆.解：程序代码：>> syms aA=[1+a,1,1,1,1;1,1+a,1,1,1;1,1,1+a,1,1;1,1,1,1+a,1;1,1,1,1,1+a]; solve=inv(A) 答案：solve =[ 1/a*(a+4)/(a+5), -1/a/(a+5), -1/a/(a+5), -1/a/(a+5), -1/a/(a+5)] [ -1/a/(a+5), 1/a*(a+4)/(a+5), -1/a/(a+5), -1/a/(a+5), -1/a/(a+5)] [ -1/a/(a+5), -1/a/(a+5), 1/a*(a+4)/(a+5), -1/a/(a+5), -1/a/(a+5)] [ -1/a/(a+5), -1/a/(a+5), -1/a/(a+5), 1/a*(a+4)/(a+5), -1/a/(a+5)] [ -1/a/(a+5), -1/a/(a+5), -1/a/(a+5), -1/a/(a+5), 1/a*(a+4)/(a+5)]实验11 矩阵的秩与向量组的极大无关组实验目的 学习利用Matlab 求矩阵的秩,作矩阵的初等行变换; 求向量组的秩与极大无关组. 求矩阵的秩86 设,815073*********⎪⎪⎪⎭⎫ ⎝⎛-------=M 求矩阵M 的秩.解：程序代码：>> M=[3,2,-1,-3,-2;2,-1,3,1,-3;7,0,5,-1,-8]; R=rank(M) 答案：R=2 向量组的秩87求向量组)0,3,0,2(),2,5,4,0(),1,1,2,1(231=--=-=ααα的秩. 解：程序代码：>> A=[1,2,-1,1;0,-4,5,-2;2,0,3,0]; R=rank(A) 答案：R =288向量组)7,5,1,3(),5,4,3,1(),1,1,1,1(),3,2,1,1(4321==-==αααα是否线性相关? 解：由>> A=[1 1 2 3;1 -1 1 1;1 3 4 5;3 1 5 7];rank(A) ans = 3即rank(A)=3 小于阶数489向量组)3,1,1(),2,1,3(),7,2,2(321=-==ααα是否线性相关? 解：由>> A3=[2,2,7;3,-1,2;1,1,3];R=rank(A3) 得 R = 3即rank(A3)=3 等于阶数3 故向量组线性无关。

八、微积分中的应用1、求极限（1）单变量函数极限： 极限：limit(fun,x,x0)左右极限：limit(fun, x, x0, ‘left ’或‘right ’) 例：lim (1)sinxx a b x xx→∞+ 程序：syms x a b;f=x*(1+a/x)^x*sin(b/x); L=limit(f,x,inf) 练习： 1) 32lim(1)xx t x→∞+2) 30tan sin limx x xx →-3) lim )x x →-∞4) limx x 5) 111lim()ln 1x x x→--6) limx π→（2）多变量函数极限：limit(limit(fun,x,x0),y,y0)或limit(limit(f,y,y0),x,x0)例：1222()sin 1(1)x y x a yx x y x y -+++程序：syms x y a;f=exp(-1/(y^2+x^2))*sin(x)^2/x^2*(1+1/y^2)^(x+a^2*y^2); limit(limit(f,x,1/sqrt(y)),y,inf) 练习：1) 00cos lim 1x x y e yx y →→++2) 22011limx y x xyx y →→-++2、求导数 求导数：dfdx, diff(f,x)求高阶导数：n nd fdx ,diff(f,x,n)例：syms x y;y=x^4;diff(y,x,2);diff(y,x,4);求偏导数：diff(diff(f,x,m),y,n) 或 diff(diff(f,y,n),x,m)例：222z x y xy =++,2zx y∂∂∂程序：syms x y;z=x^2+y^2+2*x*y;diff(diff(z,x,1),y,1); 练习：1) y =，求y ''2) 2sin y x x =，求(10)y3) x y z x y -=+,求22222,,z z zx y x y∂∂∂∂∂∂∂4) sin sin 2x t y t =⎧⎨=⎩,求22,dy d ydx dx3、求积分不定积分：int(f,x)例：syms x f;f=x^2;int(f,x)定积分和无穷积分：int(f,x,a,b)(注：a,b 可以是inf 或-inf) 例：syms x; syms x;int(exp(x),x,0,1)重积分：int(int(int(f,x,a,b),y,c,d),z,e,g)其中f 为x,y,z 的函数，x,y,z 为变量，a,b,c,d,e,g 是x,y,z 的上下限； 例：22204x y xzedzdydx ππ--⎰⎰⎰程序：syms x y z;int(int(int(4*x*z*exp(-x^2-y^2),x,0,2),y,0,pi),z,0,pi) 练习：1) sin 4cos2x x dx ⎰ 2) arctan x x dx ⎰ 3) cos ax e bx dx ⎰4)5) 21(1)x dx e +⎰6) 4dx ⎰7) 10⎰ 8) 1200sin()ydy y dx ⎰⎰9) 10dy ⎰10) 111220x x ydx dy xdz ---⎰⎰⎰4、 代数方程的求解（1） 多项式求根：roots(p)其中：p 为多项式的系数，按降幂方式形成的行向量 例如：求765422 5.2 4.8729.810x x x x x x -+-++++=的根 程序：p=[-2 5.2 -4.8 7 0 2 9.8 1] ;roots(p) 练习:求4322610x x x +++=的根 （2） 求一元函数零点：fzero(f,x0)表示求函数f 在x0附近零点；若x0为一个二维向量[a,b],则变成求函数f 在区间(a,b)内的零点；例如 :求方程30x e x --=在区间(1,2)内的一个实根 程序 :x0=[1,2] ;syms x ;f= 'exp(x)-x-3 ';fzero(f,x0) 练习 :1) 求方程3250x x --=在区间(0,3)内的实根 2) 求方程323220x x x +--=在区间(-1,0)内的实根 (3) 求代数方程组的解 solve(f1,f2,f3,……)例如：求方程组2222225x y z x y z x y z ++=⎧⎪++=⎨⎪++=⎩的解程序：syms x y z ;f1= 'x+y+z=2 ';f2= '2*x+y+2*z=2 ' ;f3= '2*x+2*y+z=5 '; [x,y,z]=solve(f1,f2,f3); 5、 Taylor 展开按x=0进行Taylor 幂级数展开：taylor(f,x,k)(注：k 表示显示前k 项，常数项，x 的一次项，x 的二次项，……x 的k-1次项) 按x=a 进行Taylor 幂级数展开：taylor(f,x,k,a) 例：syms x ;taylor(sin(x),x,5) 练习 :1) 求函数x f e =在0x =处前8项Taylor 展开式 2) 2) 求函数ln f x =在1x =处前6项Taylor 展开式6、 微分方程（组）的求解（1） 常微分方程的求解dsolve(‘e ’,’c ’,’v ’)其中：e 为微分方程，c 为初值条件，v 为微分方程中的自变量，省略时按缺省原则处理，以小写的t 为自变量。