定积分二重积分三重积分.

重积分知识点的总结一、重积分的基本概念1. 多元函数在多元函数中，自变量不再是一个，而是两个或两个以上。

例如，z=f(x,y)就是一个的二元函数。

无论是一元函数，还是二元函数，其基本概念都是“输入-处理-输出”。

其中输入就是参数，也就是变量，处理就是函数规定的运算。

这一基本概念在重积分中也是适用的。

2. 多元函数的极限多元函数的极限，与一元函数的极限类似，只是在多个自变量的情况下，我们需要考察所有自变量分别趋于一定值时的极限情况。

其中一定需要掌握的是多元函数极限的存在性问题。

3. 多元函数的连续性对于多元函数的连续性，我们同样需要关注多个自变量的变化趋势。

多元函数的连续性与一元函数的连续性类似，但要求更加严格。

在重积分中，对于多元函数的连续性是一个比较重要的概念。

4. 重积分的意义重积分的最基本的意义，就是对于多变量函数在多维空间上进行积分。

而在物理学上，重积分的意义就更加明显了。

在空间当中，一定有一个虚拟的某一点，作为观察点。

而对整个空间进行积分，就是将所有的观察点都进行积分，求得整个空间的某一个物理量。

二、重积分的性质1. 线性性质重积分的线性性质是最基本的性质之一。

它影响到重积分的很多性质，例如加减性、齐次性等都是与线性性质相关的。

2. 保号性和保序性对于多元函数来说，保号性和保序性是非常重要的性质。

在重积分中，保号性和保序性也是一个非常重要的概念，它们影响到多元函数的积分值的大小。

3. 对称性对称性在重积分中同样起到了非常重要的作用。

对称性不仅在理论证明中起到了重要作用，而且在实际应用中，对称性也常常起到了非常重要的作用。

4. 交换积分次序对于多元函数的重积分来说，交换积分次序是一个很基本的性质。

但是在实际应用中，交换积分次序同样是需要一些技巧的，有时候并不是直接可行的，需要一些特殊的条件。

5. 分部积分法分部积分法在一元函数的积分中是非常重要的一种积分方法。

而对于多元函数的重积分来说，分部积分法同样是非常重要的。

三重积分的各种计算方法计算： ()f x y z dxdydz Ω⎰⎰⎰，，. 当积分区域Ω的表面用柱(/球)坐标表示时方程简单，且被积函数 () f x y z ，， 用柱(/球)坐标表示时，可变量分离时，可将其转化为用柱(/球)坐标( )F z d d dz ρρθρθΩ⎰⎰⎰，，()2s ()in r F r drd d θϕϕθϕΩ⎰⎰⎰，或，计算三重积分比较简单。

—— 重积分的换元积分法_____________________________________________________________________三重积分的计算是化为三次积分进行的。

其实质是计算一个定积分（一重积分）和一个二重积分。

从顺序看：_____________________________________________________________________1. 如果先做定积分21() z z f x y z dz ⎰，，，再做二重积分(,)xyD F x y d σ⎰⎰，就是投影法，也即 “先一后二”。

步骤为：找Ω及在xoy 面投影区域D 。

过D 上一点() x y ，“穿线”确定z 的积分限，完成了“先一”这一步（定积分）；进而按二重积分的计算步骤计算投影区域D 上的二重积分，完成“后二”这一步，即()()21,,(,,)[(,,)]xy z x y D z x y f x y z dv f x y z dz d σΩ=⎰⎰⎰⎰⎰⎰_____________________________________________________________________2. 如果先做二重积分⎰⎰zD d z y x f σ),,(再做定积分⎰21)(c c dz z F ，就是截面法，也即“先二后一”。

步骤为：确定Ω位于平面1 z c =与2 z c =之间，即12[,]z c c ∈，过z 作平行于xoy 面的平面截Ω，截面z D 。

学院：统计与数学学院班级：信息与计算科学学号：902094135导师；毕远宏姓名：贾建慧各类积分之间的关系积分有不定积分、定积分以及二重积分，三重积分，第一类线积分，第二类线积分，第一类面积分，第二类面积分等。

我在这里只介绍我们在大学的时候学习过的几类常用积分的关系。

一、不定积分：即已知导数求原函数。

定义1:设函数f与F在区间I上都有定义。

若F′（x）=f(x),x ∈I,则称F为f在区间I上的一个原函数。

例如，13x3是x2在（—∞，＋∞）上的一个原函数，因为（13x3）＇=x2；又如-12cos2x与-12cos2x+1都是sin2x在（−∞,+∞）上的原函数，因为（-12cos2x）＇=（-12cos2x+1）＇=sin2x.定理8.1可知由于初等函数为连续函数，因此每个初等函数都有原函数（只是初等函数的原函数不一定是初等函数）当然如果一个函数存在间断点，那么此函数在其间断点所在的区间上就不一定存在原函数。

定义2:函数f在区间I上的全体原函数称为f在I上的不定积分，记作f x dx其中∫称为积分号,f x被积函数，f(x)dx为被积表达式，x为积分变量。

由定义2可知不定积分与原函数是总体与个体的关系，即若F′(x)=f(x)，那么[F(x)+C]′=f(x).(C∈R).也就是说，把f(x)积分，不一定能得到F(x)，因为F(x)+C的导数也是f(x)（C是任意常数）。

所以f(x)积分的结果有无数个，是不确定的。

我们一律用F(x)+C代替，这就称为不定积分。

即如果一个导数有原函数，那么它就有无限多个原函数。

f x dx=f x或d f x dx=f x dx；性质1：ddx性质2：F＇x dx=F x+C或dF x+C；性质3：αf x±βg x dx=αf x dx±βg x dx，α,β为非零常数。

二、定积分:定积分就是求函数f x在区间a,b中图线下包围的面积。

即由 y=0, x=a ,x=b, y=f x所围成图形的面积。

重积分的计算方法重积分包括二重积分和三重积分，它是定积分的推广；被积函数由一元函数f（x）推广为二元函数f（x,y），三元函数（fx,y,z）;积分范围由数轴上的区域推广为平面域（二重积分）和空间域（三重积分）。

我个人在学习与复习多重积分这一块时，感到多重积分的计算比较繁琐，而在日常生活中多重积分有着很多的应用。

通过在图书馆查阅资料、以及老师的指点，重积分的计算方法还是有规律可循的。

为了更好的应用重积分，本人结合前人的经验，在这里介绍几种常用的重积分计算方法，以及一些小技巧。

着重介绍累次积分的计算与变量代换。

一．二重积分的计算1．常用方法（1）化累次积分计算法对于常用方法我们先看两个例子对于重积分的计算主要采用累次积分法，即把一个二重积分表达为一个二次积分，通过两次定积分的计算求得二重积分值，分析上面的例子累次积分法其主要步骤如下：第一步：画出积分区域D的草图；第二步：按区域D和被积函数的情况选择适当的积分次序，并确定积分的上、下限；第三步：计算累次积分。

需要强调一点的是，累次积分要选择适当的积分次序。

积分次序的不同将影响计算的繁简，有些题这两种次序的难易程度可以相差很大，甚至对一种次序可以“积出来”，而对另一种次序却“积不出来”。

所以，适当选择积分次序是个很重要的工作。

选择积分次序的原则是：尽可能将区域少分块，以简化计算过程；第一次积分的上、下限表达式要简单，并且容易根据第一次积分的结果作第二次积分。

（2）变量替换法着重看下面的例子：在计算定积分时，求积的困难在于被积函数的原函数不易求得。

从而适当地在计算重积分时，求积的困难来自两个方面，除了被积函数的原因以外还在而且，有时候其积分区域往往成为困难的主要方面。

利用换元法的好处是可以把被积函数的形状进行转化，以便于用基本求积公式。

于积分区域的多样性。

为此，针对不同的区域要讨论重积分的各种不同算法。

（3）极坐标变换公式（主要是∫∫f(x,y)dxdy=∫∫f(pcosθ,psinθ)pdpdθ）下面看一个例子：计算二重积分时，要从被积函数和积分域两个方面来考虑如何适当地选择坐标系，如能采用适当的坐标系，往往可以收到事半功倍的效果。

三重积分的各种计算方法计算： ()f x y z dxdydz Ω⎰⎰⎰，，. 当积分区域Ω的表面用柱(/球)坐标表示时方程简单，且被积函数 () f x y z ，， 用柱(/球)坐标表示时，可变量分离时，可将其转化为用柱(/球)坐标( )F z d d dz ρρθρθΩ⎰⎰⎰，，()2s ()in r F r drd d θϕϕθϕΩ⎰⎰⎰，或，计算三重积分比较简单。

—— 重积分的换元积分法_____________________________________________________________________三重积分的计算是化为三次积分进行的。

其实质是计算一个定积分（一重积分）和一个二重积分。

从顺序看：_____________________________________________________________________1. 如果先做定积分21() z z f x y z dz ⎰，，，再做二重积分(,)xyD F x y d σ⎰⎰，就是投影法，也即 “先一后二”。

步骤为：找Ω及在xoy 面投影区域D 。

过D 上一点() x y ，“穿线”确定z 的积分限，完成了“先一”这一步（定积分）；进而按二重积分的计算步骤计算投影区域D 上的二重积分，完成“后二”这一步，即()()21,,(,,)[(,,)]xy z x y D z x y f x y z dv f x y z dz d σΩ=⎰⎰⎰⎰⎰⎰_____________________________________________________________________2. 如果先做二重积分⎰⎰zD d z y x f σ),,(再做定积分⎰21)(c c dz z F ，就是截面法，也即“先二后一”。

步骤为：确定Ω位于平面1 z c =与2 z c =之间，即12[,]z c c ∈，过z 作平行于xoy 面的平面截Ω，截面z D 。

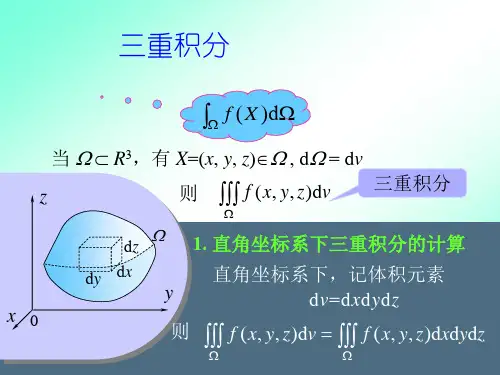
三重积分及其计算法二重积分的被积函数是一个二元函数，它的积分域是—平面区域.如果考虑三元函数f(x,y,z)在一空间区域(V)上的积分，就可得到三重积分的概念。

三重积分的概念设函数u=f(x,y,z)在空间有界闭区域(V)任意划分成n 个子域(△V 1),(△V 2),(△V 3),…,(△V n ),它们的体积分别记作△V k (k=1,2,…,n).在每一个子域上任取一点，并作和数如果不论△V k 怎样划分，点怎样选取，当n→+∞而且最大的子域直径δ→0时，这个和数的极限都存在，那末此极限就称为函数在域(V)上的三重积分,记作：即：如果f(x,y,z)在域(V)上连续，那末此三重积分一定存在。

对于三重积分没有直观的几何意义，但它却有着各种不同的物理意义。

直角坐标系中三重积分的计算方法这里我们直接给出三重积分的计算公式，具体它是怎样得来的，请大家参照有关书籍。

直角坐标系中三重积分的计算公式为：此公式是把一个三重积分转化为一个定积分与一个二重积分的问题，根据我们前面所学的结论即可求出。

例题：求，其中(V)是由平面x=0,y=0,z=0及x+y+z=1所围成的区域.解答：把I 化为先对z 积分，再对y 和x 积分的累次积分，那末应把(V)投影到xOy 平面上,求出投影域(σ),它就是平面x+y+z=1与xOy 平面的交线和x 轴、y 轴所围成的三角区域.我们为了确定出对z 积分限,在(σ)固定点(x,y),通过此点作一条平行于z 的直线,它与(V)上下边界的交点的竖坐标：z=0与z=1-x-y，这就是对z积分的下限与上限，于是由积分公式得：其中(σ)为平面区域：x≥0，y≥0，x+y≤1，如下图红色阴影部分所示：再把(σ)域上的二重积分化成先对y后对x的累次积分，得：柱面坐标系中三重积分的计算法我们先来学习一下空间中的点用极坐标的表示方法。

平面上点P可以用极坐标(ρ,θ)来确定,因此空间中的点P可用数组(ρ,θ,z)来表示.显然，空间的点P与数组(ρ,θ,z)之间的对应关系是一一对应关系,数组(ρ,θ,z)称为空间点P的柱面坐标.它与直角坐标的关系为：构成柱面坐标系的三族坐标面分别为：ρ=常数：以z轴为对称轴的同轴圆柱面族，θ=常数：通过z轴的半平面族，z=常数：与z轴垂直的平面族.因此，每三个这样的坐标面确定着空间的唯一的一点，由于利用了圆柱面，所以称为柱面坐标。

《高等数学》中的积分学总结高等数学中涉及的积分类型主要有：定积分（含广义积分）、二重积分、三重积分、曲线积分（对弧长、对坐标）、曲面积分（对面积、对坐标）。

一、符号形式1()baI f x dx =⎰；2(,)DI f x y d σ=⎰⎰；3(,,)I f x y z dV Ω=⎰⎰⎰；4(,,)CI f x y z ds =⎰；5CCI F dr Pdx Qdy Rdz ==++⎰⎰；6(,,)I f x y z dS ∑=⎰⎰；7I F ndS F dS Pdydz Qdzdx Rdxdy ∑∑∑===++⎰⎰⎰⎰⎰⎰二、共同点2.1 定义方法：划分—>微元—>求和—>取极限 2.2 性质：线性性质、可加性、估值三、不同点ds功、流量、环量、通量dS流量、通量四、重要联系及公式4.1 Newton-Leibniz 公式：()()()ba f x dx Fb F a =-⎰4.2 Green 公式： 环量—旋度形式：()CDDQ P x y DPdx Qdy rotF kd F kd d σσσ∂∂∂∂+==∇⨯=-⎰⎰⎰⎰⎰⎰⎰通量—散度形式：()CDDQPx yDPdy Qdx F nd divFd d σσσ∂∂∂∂-===+⎰⎰⎰⎰⎰⎰⎰4.3 Stokes 公式：()()()CQQRP RP y zz x xy Pdx Qdy Rdz rotF ndS F ndSdydz dzdx dxdy∑∑∂∂∂∂∂∂∂∂∂∂∂∂∑++==∇⨯=-+-+-⎰⎰⎰⎰⎰⎰⎰4.4 Gauss 公式：()QPR x yz Pdydz Qdzdx Rdxdy F ndS divFdV FdVdV∑∑ΩΩ∂∂∂∂∂∂Ω++===∇=++⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰五、基本计算方法5.1 定积分方法：凑微分法、换元法、分部积分法 特殊结论：（1）对称性与奇偶性：02(),()()()0,()()aaaf x dx f x f x f x dx f x f x -⎧-=⎪=⎨⎪-=-⎩⎰⎰（2）周期性：0()()a T Taf x dx f x d x +=⎰⎰（3）无界性：(),(),(),()A bb Aaaf x dx f x dx f x dx f x dx -++∞-∞⎰⎰⎰⎰2(,)DI f x y d σ=⎰⎰，其中D 为平面有界区域。

利用投影法选取重积分的上、下限[摘要]投影法是数学中的化归思想在积分学中直接运用的一种方法。

利用投影法分别选取了定积分、二重积分、三重积分的上、下限，重点讲解重积分上、下限的选取。

此方法学生易于掌握，同时可以缩短学习的时间。

[关键词]投影法；二重积分；三重积分；上限；下限[]O172 []A []2095-3712（2014）13-0093-02[作者简介]郭新（1977―），女，河南濮阳人，硕士，濮阳职业技术学院数学与信息工程系讲师，研究方向：概率论与高等数学教学。

在计算二重积分和三重积分这样的重积分时，一般都是先将它们化成相应的累次积分。

在化的过程中，往往要用到投影法确定积分的上、下限，然后再运用定积分的计算方法来计算。

一、二重积分上、下限的选取在直角坐标系下计算二重积分Df（x，y）dσ的方法在其定义中已经给出，但这种方法计算起来比较麻烦，且有很大的局限性。

所以常用的计算方法是通过化二重积分为两次定积分或累次积分法，在计算中使用投影法可以使计算更加简单。

在计算时把曲项柱体投影在xy平面上，得到平面积分区域D，D即为xy平面上由平面曲线围成的平面区域，故可分为X型与Y型。

Df（x，y）dσX型∫badx∫y2（x）y1（x）f（x，y）dyDf（x，y）dσY型∫dcdy∫φ2（y）φ1（y）f（x，y）dy从中可以看到，二重积分的上、下限实际上是定积分的上、下限与被积函数f（x，y）。

二、三重积分上、下限的选取在直角坐标系下对三重积分进行计算，在将三重积分化为累次积分时，可以使用坐标面投影法和坐标轴投影法，具体方法的使用还要看实际问题的情况，适合哪个方法就用哪个方法。

（一）坐标面投影法如图1，闭区域Ω={（（x，y，z）|z1（x，y）<Z2（X，Y），（X，Y）∈D}，D为XOY平面上的平区域。

区域Ω的特点为：图1 坐标面投影法过任意点（x，y）作一条平行于Z 轴且垂直穿过闭区域Ω的直线，该直线与区域Ω的边界至多有两个交点z1（x，y）和z2（x，y）。