2 正态分布

构成二维正态分布的条件二维正态分布是二维随机变量的分布形式之一，它是指当两个随机变量X和Y满足一定条件时，它们的联合分布是二维正态分布。

构成二维正态分布的条件包括均值、方差和协方差矩阵。

1. 均值：对于二维正态分布来说，均值是指X和Y的期望值。

假设X的均值为μ1，Y的均值为μ2，则二维正态分布的均值为(μ1, μ2)。

2. 方差：方差是衡量随机变量分布的离散程度的指标。

对于二维正态分布来说，X和Y的方差分别为σ1^2和σ2^2。

方差越大，随机变量的取值越分散。

3. 协方差矩阵：协方差矩阵描述了X和Y之间的线性关系。

对于二维正态分布来说，协方差矩阵是一个2x2的矩阵，记为Σ。

其中，Σ(1,1)表示X的方差，Σ(2,2)表示Y的方差，Σ(1,2)和Σ(2,1)表示X 和Y的协方差。

协方差矩阵的对角线元素即为各自的方差，非对角线元素表示X和Y之间的相关程度。

当协方差为正值时，表示X和Y呈正相关；当协方差为负值时，表示X和Y呈负相关。

4. 独立性：如果X和Y是独立的，那么它们的协方差为0，即Σ(1,2) = Σ(2,1) = 0。

当X和Y是独立的时候，它们的联合分布就是二维正态分布。

二维正态分布在概率统计学中具有广泛的应用。

例如，在金融领域中，二维正态分布可以用来描述股票收益率之间的关系；在生物学研究中，二维正态分布可以用来描述两个特征之间的相关性。

通过对二维正态分布的建模和分析，可以帮助我们更好地理解和预测随机变量之间的关系。

总结起来，构成二维正态分布的条件包括均值、方差和协方差矩阵。

通过对这些条件的研究和分析，可以得到二维正态分布的概率密度函数，进而对随机变量之间的关系进行建模和预测。

二维正态分布在实际应用中具有重要的意义，对于理解和分析随机变量之间的关系具有重要的参考价值。

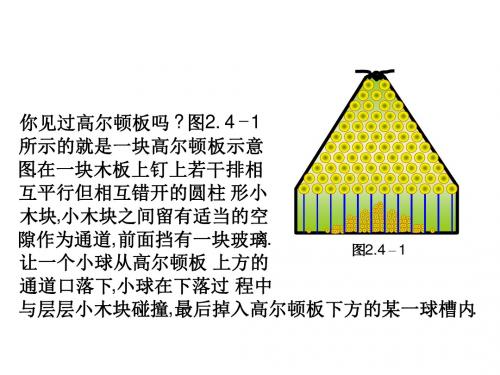
正态分布是统计学中一种重要的概率分布，也被称为高斯分布。

它在实际应用中非常常见，可以用来描述许多自然现象和社会现象，比如身高、体重、芳龄等。

在正态分布中，均值和标准差是决定分布形态的两个关键参数。

本文将深入探讨正态分布的概念、特性和应用，并解读与计算正态分布的2σ概率。

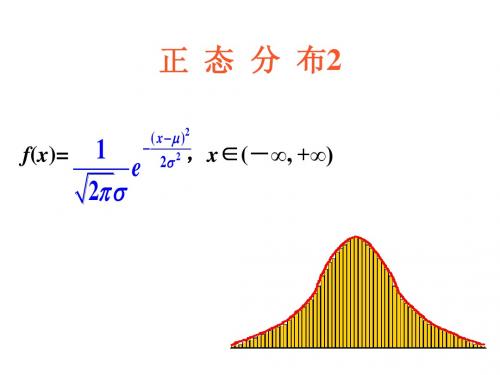
1. 正态分布的概念及特性1.1 正态分布的定义正态分布是一种钟形对称的连续型概率分布，其密度函数可以用数学公式表示为：f(x) = (1 / (σ * √(2 * π))) * e^(-((x - μ)^2) / (2 * σ^2))其中，μ为分布的均值，σ为分布的标准差，e为自然对数的底。

1.2 正态分布的特性正态分布具有以下几个重要特性： - 曲线对称：正态分布的密度曲线关于均值对称，均值处为曲线的中心位置。

- 唯一峰值：正态分布只有一个峰值，即均值所在处，两侧的概率逐渐减小。

- 形态稳定：正态分布的形态由均值和标准差唯一决定，不受具体数值的影响。

- 标准正态分布：当均值μ为0，标准差σ为1时，称为标准正态分布。

2. 正态分布的应用2.1 统计推断正态分布在统计学中具有重要的应用，尤其是在统计推断中起到关键作用。

根据中心极限定理，大量独立同分布的随机变量的均值近似服从正态分布。

这使得正态分布可以用来进行参数估计和假设检验，对总体的特征进行推断。

2.2 质量控制正态分布在质量控制领域中也扮演着重要角色。

许多生产过程的输出结果往往服从正态分布。

通过对生产过程进行抽样和统计分析，可以计算出均值和标准差，进而判断产品质量的合格率，并进行异常点检测和质量改进。

2.3 风险管理正态分布在金融和风险管理领域中广泛应用。

通过建立资产收益率的正态分布模型，可以估计投资风险和收益的分布情况，从而更好地制定投资策略和管理风险。

3. 正态分布2σ概率的解读与计算在正态分布中，均值加减2倍标准差的范围约包含95.45%的观测值。

这意味着，对于一个服从正态分布的随机变量，其取值在均值加减2倍标准差范围内的概率为0.9545。

二维正态分布概率密度公式
二维正态分布，也称为双变量正态分布或多元正态分布，是统计学中最重要的分布形式之一，在随机可观测变量具有两个或多个未知参数的情况下，它反映了参数的概率分布，它的概率密度函数由公式表示：
f(x,y)=1/2πσxσy e^(-(x^2/2σx^2+y^2/2σy^2)
其中，x,y分别表示变量的两个参数，σx和σy分别为变量的标准差。

正态分布是各种统计推断方法的基础，当收集的样本数据遵循正态分布时，通常用正态分布和正态分布概率密度函数来描述样本分布。

可以使用中心极限定理证明，即使相关数据不是正态分布，但样本量足够大时，他们的分布也会接近正态分布，这也是大量研究采用正态分布的原因。

因此，正态分布概率密度函数可以用来描述样本集中每个变量的概率分布，完整地表达变量与其未知参数之间的关系。

它反映了各种统计推断方法的基础，也是大数据分析中广泛使用和推广的多元正态分布形式。

二维正态分布定义
二维正态分布是指具有两个连续随机变量的联合分布服从正态分布。

它可以由一对连续随机变量X和Y组成，其概率密度
函数可以表示为：
f(x,y) = 1 / (2πσxσy√(1-ρ^2)) * exp(-1 / (2(1-ρ^2)) * ((x-
μx)^2/σx^2 + (y-μy)^2/σy^2 - 2ρ(x-μx)(y-μy)/(σxσy)))
其中，μx和μy分别是X和Y的均值，σx和σy分别是X和Y 的标准差，ρ是X和Y之间的相关系数。

二维正态分布具有以下性质：
1. X和Y的边缘分布分别为正态分布，即X和Y分别服从正
态分布。

2. X和Y之间的相关系数ρ决定了它们的线性关系的强度和
方向。

当ρ为0时，X和Y相互独立。

当ρ为正数时，X和Y
正相关；当ρ为负数时，X和Y负相关。

3. 二维正态分布具有椭圆形状，其椭圆的形状和大小由σx，
σy和ρ决定。

若σx=σy且ρ=0，椭圆的主轴与坐标轴平行，
表示X和Y相互独立，具有相同的方差；若σx>σy或σx<σy，椭圆的主轴与坐标轴不平行，表示X和Y具有不同的方差；
当ρ≠0时，椭圆发生旋转，表示X和Y之间存在相关关系。

4. 二维正态分布的期望向量为(μx, μy)，协方差矩阵为：
Cov(X,Y) = [[σx^2, ρσxσy],
[ρσxσy, σy^2]]
协方差矩阵表示X和Y之间的相关性，对角线上的元素是
方差，非对角线上的元素是协方差。