正态分布讲解(含标准表)

标准正态分布3个常用公式标准正态分布在统计学中可是个相当重要的概念，它有三个常用公式，咱今儿个就来好好说道说道。

先来讲讲第一个常用公式，那就是标准正态分布的概率密度函数公式。

这公式看起来挺复杂，其实理解起来也没那么难。

它就像是给每个数值都赋予了一个特定的“权重”，告诉我们某个数值出现的可能性有多大。

我记得之前有一次，我们班组织了一场数学知识竞赛。

有个小组的同学在计算一个数据出现的概率时，就卡壳了。

我在旁边看着，心里那个着急呀。

后来我就给他们解释，这就跟标准正态分布的概率密度函数有关系。

就好比咱们扔骰子，每个点数出现都有一定的概率，而标准正态分布里的数值也是这样，这个公式能帮咱们算出每个数值出现的大概可能性。

再来说说第二个常用公式，就是标准正态分布的累积分布函数公式。

这玩意儿能帮我们算出某个数值及小于这个数值的概率总和。

有一回，学校组织义卖活动，我们要统计不同价格区间的商品销售情况。

这时候，标准正态分布的累积分布函数公式就派上用场啦。

通过这个公式，我们能大致估计出某个价格以下的商品销售占比，从而更好地规划后续的义卖策略。

最后是第三个常用公式，标准正态分布的分位数公式。

它能让我们找到特定概率对应的数值。

记得有一次做数学实验，要分析一组学生的考试成绩。

我们想知道在某个优秀率下对应的分数是多少，这时候就得靠标准正态分布的分位数公式来帮忙啦。

总之，这三个标准正态分布的常用公式在很多领域都有着重要的应用。

不管是科学研究、经济分析，还是日常生活中的各种数据处理，它们都能帮咱们更好地理解和处理数据，做出更准确的判断和决策。

希望通过我的这些讲解，能让您对标准正态分布的这三个常用公式有更清晰的认识和理解。

多去实际应用中体会它们的妙处，您会发现统计学的世界其实挺有趣的！。

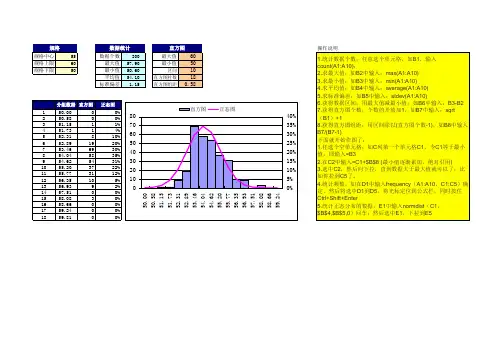
操作说明
1.统计数据个数；任意选个单元格，如B1，输入
count(A1:A10)；
2.求最大值；如B2中输入：max(A1:A10)
3.求最小值；如B3中输入：min(A1:A10)
4.求平均值；如B4中输入：average(A1:A10)
5.求标准偏差：如B5中输入：stdev(A1:A10)
6.获得数据区间；用最大值减最小值；如B6中输入：B3-B2
7.获得直方图个数；个数的开放加1
，如B7中输入：sqrt
（B1）+1
8.获得直方图组距；用区间除以(直方图个数-1)，如B8中输入B7/(B7-1)
下面就开始作图了：
1.任选个空单元格：如C列第一个单元格C1，令C1等于最小值，即输入=B3
2.在C2中输入=C1+$B$8 (最小值逐渐累加，绝对引用)
3.选中C2，然后向下拉，直到数据大于最大值就可以了；比如你拉到C5了。

4.统计频数，如在D1中输入frequency（A1:A10，C1:C5）确定，然后将选中D1到D5，将光标定位到公式栏，同时按住Ctrl+Shift+Enter
5.统计正态分布的数据，E1中输入normdist（C1，
$B$4,$B$5,0）回车；然后选中E1，下拉到E5。

《正态分布》说课稿正态分布是统计学中非常重要的一个概念，它描述了大量随机变量的分布规律，被广泛应用于各个领域的数据分析和预测中。

本文将介绍正态分布的基本概念、性质、应用以及如何利用正态分布进行统计推断。

一、正态分布的基本概念1.1 正态分布的定义：正态分布又称高斯分布，是一种连续概率分布，其概率密度函数呈钟形曲线，左右对称，中间最高。

1.2 正态分布的特点：正态分布具有唯一的均值和标准差，均值决定了曲线的中心位置，标准差决定了曲线的宽度。

1.3 正态分布的标准化：通过标准化可以将正态分布转化为标准正态分布，即均值为0，标准差为1的正态分布。

二、正态分布的性质2.1 正态分布的均值和中位数相等：正态分布的均值和中位数相等，即曲线对称中心位置处的值。

2.2 正态分布的68-95-99.7法则：约68%的数据落在均值附近的一个标准差范围内，约95%的数据落在两个标准差范围内，约99.7%的数据落在三个标准差范围内。

2.3 正态分布的线性组合仍然是正态分布：对于正态分布的线性组合，如两个正态分布的和或差，仍然是正态分布。

三、正态分布的应用3.1 在自然科学中的应用：正态分布常用于测量误差、实验数据分析等领域，如物理学、化学等。

3.2 在社会科学中的应用：正态分布被广泛应用于人口统计、心理学研究、经济学分析等领域。

3.3 在工程技术中的应用：正态分布在质量控制、可靠性分析、风险评估等方面有重要应用。

四、利用正态分布进行统计推断4.1 正态分布的参数估计：通过样本数据估计总体的均值和标准差，得到对总体的估计。

4.2 正态分布的假设检验：利用正态分布进行假设检验，判断总体参数是否符合某种假设。

4.3 正态分布的置信区间估计：通过正态分布的性质，构建总体参数的置信区间，对总体参数进行估计。

五、结语正态分布作为统计学中重要的概念，具有丰富的性质和广泛的应用。

通过深入理解正态分布的基本概念和性质，我们可以更好地应用正态分布进行数据分析和推断，为各个领域的研究和实践提供有力支持。

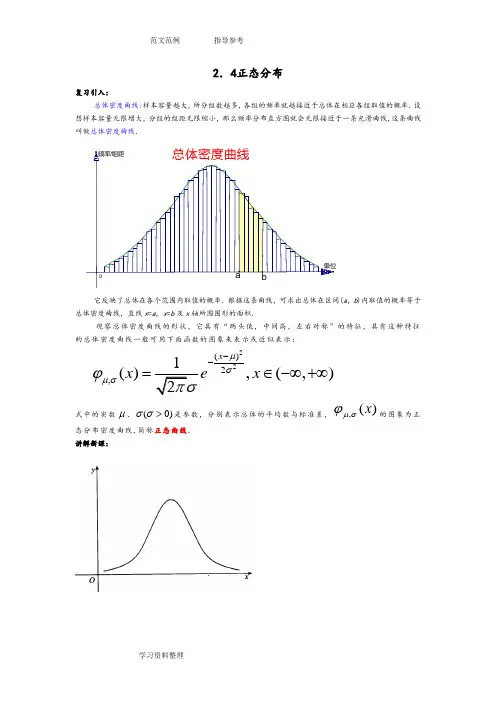
2．4正态分布复习引入：总体密度曲线:样本容量越大，所分组数越多，各组的频率就越接近于总体在相应各组取值的概率．设想样本容量无限增大，分组的组距无限缩小，那么频率分布直方图就会无限接近于一条光滑曲线,这条曲线叫做总体密度曲线． 总体密度曲线b 单位O 频率/组距a它反映了总体在各个范围内取值的概率．根据这条曲线，可求出总体在区间(a ，b )内取值的概率等于总体密度曲线，直线x =a ，x =b 及x 轴所围图形的面积．观察总体密度曲线的形状，它具有“两头低，中间高，左右对称”的特征，具有这种特征的总体密度曲线一般可用下面函数的图象来表示或近似表示：22()2,1(),(,)2x x e x μσμσϕπσ--=∈-∞+∞ 式中的实数μ、)0(>σσ是参数，分别表示总体的平均数与标准差，,()x μσϕ的图象为正态分布密度曲线,简称正态曲线．讲解新课：一般地，如果对于任何实数a b <，随机变量X 满足,()()b aP a X B x dx μσϕ<≤=⎰, 则称 X 的分布为正态分布（normal distribution ) ．正态分布完全由参数μ和σ确定，因此正态分布常记作),(2σμN ．如果随机变量 X 服从正态分布，则记为X ～),(2σμN .经验表明，一个随机变量如果是众多的、互不相干的、不分主次的偶然因素作用结果之和，它就服从或近似服从正态分布．例如，高尔顿板试验中，小球在下落过程中要与众多小木块发生碰撞，每次碰撞的结果使得小球随机地向左或向右下落，因此小球第1次与高尔顿板底部接触时的坐标 X 是众多随机碰撞的结果，所以它近似服从正态分布．在现实生活中，很多随机变量都服从或近似地服从正态分布．例如长度测量误差；某一地区同年龄人群的身高、体重、肺活量等；一定条件下生长的小麦的株高、穗长、单位面积产量等；正常生产条件下各种产品的质量指标（如零件的尺寸、纤维的纤度、电容器的电容量、电子管的使用寿命等）；某地每年七月份的平均气温、平均湿度、降雨量等；一般都服从正态分布．因此，正态分布广泛存在于自然现象、生产和生活实际之中．正态分布在概率和统计中占有重要的地位．说明:1参数μ是反映随机变量取值的平均水平的特征数，可以用样本均值去佑计；σ是衡量随机变量总体波动大小的特征数，可以用样本标准差去估计．2.早在 1733 年，法国数学家棣莫弗就用n ！的近似公式得到了正态分布．之后，德国数学家高斯在研究测量误差时从另一个角度导出了它，并研究了它的性质，因此，人们也称正态分布为高斯分布．2．正态分布),(2σμN ）是由均值μ和标准差σ唯一决定的分布 通过固定其中一个值，讨论均值与标准差对于正态曲线的影响3．通过对三组正态曲线分析，得出正态曲线具有的基本特征是两头底、中间高、左右对称 正态曲线的作图，书中没有做要求，教师也不必补上 讲课时教师可以应用几何画板，形象、美观地画出三条正态曲线的图形，结合前面均值与标准差对图形的影响，引导学生观察总结正态曲线的性质4．正态曲线的性质：（1）曲线在x 轴的上方，与x 轴不相交（2）曲线关于直线x=μ对称（3）当x=μ时，曲线位于最高点（4）当x ＜μ时，曲线上升（增函数）；当x ＞μ时，曲线下降（减函数） 并且当曲线向左、右两边无限延伸时，以x 轴为渐近线，向它无限靠近（5）μ一定时，曲线的形状由σ确定σ越大，曲线越“矮胖”，总体分布越分散；σ越小．曲线越“瘦高”．总体分布越集中：五条性质中前三条学生较易掌握，后两条较难理解，因此在讲授时应运用数形结合的原则，采用对比教学5．标准正态曲线:当μ=0、σ=l 时，正态总体称为标准正态总体，其相应的函数表示式是2221)(x e x f -=π，（-∞＜x ＜+∞）其相应的曲线称为标准正态曲线标准正态总体N （0，1）在正态总体的研究中占有重要的地位 任何正态分布的概率问题均可转化成标准正态分布的概率问题讲解范例：例1．给出下列三个正态总体的函数表达式，请找出其均值μ和标准差σ （１）),(,21)(22+∞-∞∈=-x e x f x π（２）),(,221)(8)1(2+∞-∞∈=--x e x f x π （３）22(1)2(),(,)2x f x e x π-+=∈-∞+∞ 答案：(1)0，1；(2)1，2；(3)-1，0.5例2求标准正态总体在（-1，2）内取值的概率．解：利用等式)()(12x x p Φ-Φ=有)([]}{11)2()1()2(--Φ--Φ=-Φ-Φ=p=1)1()2(-Φ+Φ=0.9772＋0.8413－1=0.8151．1.标准正态总体的概率问题: xy对于标准正态总体N （0，1），)(0x Φ是总体取值小于0x 的概率，即 )()(00x x P x <=Φ， 其中00>x ，图中阴影部分的面积表示为概率0()P x x < 只要有标准正态分布表即可查表解决.从图中不难发现:当00<x 时，)(1)(00x x -Φ-=Φ；而当00=x 时，Φ（0）=0.5 2.标准正态分布表标准正态总体)1,0(N 在正态总体的研究中有非常重要的地位，为此专门制作了“标准正态分布表”．在这个表中，对应于0x 的值)(0x Φ是指总体取值小于0x 的概率，即)()(00x x P x <=Φ，)0(0≥x ．若00<x ，则)(1)(00x x -Φ-=Φ．利用标准正态分布表，可以求出标准正态总体在任意区间),(21x x 内取值的概率，即直线1x x =，2x x =与正态曲线、x 轴所围成的曲边梯形的面积1221()()()P x x x x x <<=Φ-Φ． 3．非标准正态总体在某区间内取值的概率:可以通过)()(σμ-Φ=x x F 转化成标准正态总体，然后查标准正态分布表即可 在这里重点掌握如何转化 首先要掌握正态总体的均值和标准差，然后进行相应的转化4.小概率事件的含义发生概率一般不超过5％的事件，即事件在一次试验中几乎不可能发生假设检验方法的基本思想:首先，假设总体应是或近似为正态总体，然后，依照小概率事件几乎不可能在一次试验中发生的原理对试验结果进行分析假设检验方法的操作程序，即“三步曲”一是提出统计假设，教科书中的统计假设总体是正态总体；二是确定一次试验中的a 值是否落入(μ-3σ，μ+3σ)；三是作出判断讲解范例：例1. 若x ～N (0,1),求(l)P (-2.32<x <1.2)；(2)P (x >2).解：(1)P (-2.32<x <1.2)=Φ(1.2)-Φ(-2.32)=Φ(1.2)-[1-Φ(2.32)]=0.8849-(1-0.9898)=0.8747.(2)P (x >2)=1-P (x <2)=1-Φ(2)=l-0.9772=0.0228.例2．利用标准正态分布表，求标准正态总体在下面区间取值的概率：(1)在N(1,4)下，求)3(F（2）在N （μ，σ2）下，求Ｆ（μ－σ，μ＋σ）；Ｆ（μ－1.84σ，μ＋1.84σ）；Ｆ（μ－2σ，μ＋2σ）；Ｆ（μ－3σ，μ＋3σ） 解：（１）)3(F ＝)213(-Φ＝Φ（1）＝0.8413 （２）Ｆ（μ＋σ）＝)(σμσμ-+Φ＝Φ（1）＝0.8413 Ｆ（μ－σ）＝)(σμσμ--Φ＝Φ（－1）＝１－Φ（1）＝１－0.8413＝0.1587 Ｆ（μ－σ，μ＋σ）＝Ｆ（μ＋σ）－Ｆ（μ－σ）＝0.8413－0.1587＝0.6826Ｆ（μ－1.84σ，μ＋1.84σ）＝Ｆ（μ＋1.84σ）－Ｆ（μ－1.84σ）＝0.9342Ｆ（μ－2σ，μ＋2σ）＝Ｆ（μ＋2σ）－Ｆ（μ－2σ）＝0.954Ｆ（μ－3σ，μ＋3σ）＝Ｆ（μ＋3σ）－Ｆ（μ－3σ）＝0.997对于正态总体),(2σμN 取值的概率：68.3%2σx 95.4%4σx 99.7%6σx在区间（μ-σ，μ+σ）、（μ-2σ，μ+2σ）、（μ-3σ，μ+3σ）内取值的概率分别为68.3%、95.4%、99.7% 因此我们时常只在区间（μ-3σ，μ+3σ）内研究正态总体分布情况，而忽略其中很小的一部分 例3．某正态总体函数的概率密度函数是偶函数，而且该函数的最大值为π21，求总体落入区间（－1.2，0.2）之间的概率解：正态分布的概率密度函数是),(,21)(222)(+∞-∞∈=--x e x f x σμσπ，它是偶函数，说明μ＝0，)(x f 的最大值为)(μf ＝σπ21，所以σ＝1，这个正态分布就是标准正态分布( 1.20.2)(0.2)( 1.2)(0.2)[1(1.2)](0.2)(1.2)1P x -<<=Φ-Φ-=Φ--Φ=Φ+Φ- 教学反思：1．在实际遇到的许多随机现象都服从或近似服从正态分布 在上一节课我们研究了当样本容量无限增大时，频率分布直方图就无限接近于一条总体密度曲线，总体密度曲线较科学地反映了总体分布 但总体密度曲线的相关知识较为抽象，学生不易理解，因此在总体分布研究中我们选择正态分布作为研究的突破口 正态分布在统计学中是最基本、最重要的一种分布 2．正态分布是可以用函数形式来表述的 其密度函数可写成：22()21(),(,)2x f x e x μσπσ--=∈-∞+∞， （σ＞0）由此可见，正态分布是由它的平均数μ和标准差σ唯一决定的 常把它记为),(2σμN 3．从形态上看，正态分布是一条单峰、对称呈钟形的曲线，其对称轴为x=μ，并在x=μ时取最大值 从x=μ点开始，曲线向正负两个方向递减延伸，不断逼近x 轴，但永不与x 轴相交，因此说曲线在正负两个方向都是以x 轴为渐近线的4．通过三组正态分布的曲线，可知正态曲线具有两头低、中间高、左右对称的基本特征。

正态分布通俗解释
正态分布是一种概率分布，也称为高斯分布。

它是由柯西在19世纪末提出的，是统计学中最常见的分布之一。

正态分布的特点是数据呈现“钟型分布”，即以平均数为中心，向两侧延伸，两侧的数据出现次数逐渐减少。

通俗来讲，正态分布就是指一组数据在统计上呈现“正常分布”的状态。

这种分布的数据往往是由许多不同的因素共同作用而产生的，不存在极端值的影响。

因此，在实际应用中，正态分布往往被用于描述人类智力、体重、身高等方面的分布情况。

正态分布的另一个特点是其满足中心极限定理。

这一定理指出，当样本容量足够大时，任何给定的样本的平均数的分布都将接近正态分布。

因此，正态分布在实际应用中往往被用于描述大样本的分布情况。

例如，在质量检测中，如果样本容量足够大，则样本的质量平均数的分布往往接近正态分布。

正态分布还具有很多其他的特点，例如其概率密度函数的形式等。

如
果您想了解更多关于正态分布的知识，可以咨询相关的数学或统计学资料。

正态分布完整课件一、教学内容本节课的教学内容选自人教版小学数学六年级下册第117页至119页，主要学习了正态分布的概念及其图形表示。

通过本节课的学习，让学生能够理解正态分布的特点，学会绘制正态分布图，并能够运用正态分布解决实际问题。

二、教学目标1. 理解正态分布的概念，掌握正态分布图的绘制方法。

2. 能够运用正态分布解决实际问题，提高解决问题的能力。

3. 培养学生的观察能力、动手操作能力和团队协作能力。

三、教学难点与重点重点：正态分布的概念及其图形表示。

难点：正态分布图的绘制方法和在实际问题中的运用。

四、教具与学具准备教具：PPT、黑板、粉笔、正态分布图模板。

学具：笔记本、尺子、圆规、剪刀、彩笔。

五、教学过程1. 情景引入：教师通过展示一组身高数据，引导学生观察数据的分布情况，引发学生对分布图的兴趣。

2. 自主学习：学生自主阅读教材，了解正态分布的概念，并尝试绘制正态分布图。

3. 课堂讲解：教师通过PPT讲解正态分布的特点，演示正态分布图的绘制方法，并解释正态分布在实际生活中的应用。

4. 动手操作：学生分组合作，根据给定的数据绘制正态分布图，并交流分享绘制心得。

5. 例题讲解：教师通过PPT展示典型例题，讲解解题思路，引导学生运用正态分布解决实际问题。

6. 随堂练习：学生独立完成随堂练习题，巩固所学知识。

8. 课后作业：学生完成课后作业，进一步巩固正态分布的知识。

六、板书设计板书内容：正态分布的特点、正态分布图的绘制方法、正态分布的应用。

七、作业设计数据：一组学生的身高（单位：cm）：140, 145, 150, 155, 160, 165, 170, 175, 180。

答案：略答案：略八、课后反思及拓展延伸1. 课后反思：本节课通过引导学生观察实际数据，激发学生对正态分布的兴趣。

在课堂讲解过程中，注意运用PPT和黑板辅助教学，使学生更好地理解正态分布的概念和图形表示。

同时，通过分组合作和动手操作，培养学生的团队协作能力和观察能力。

正态分布知识点总结正态分布的定义：如果随机变量的总体密度曲线是由或近似地由下面的函数给定：xR，则称服从正态分布，这时的总体分布叫正态分布，其中表示总体平均数，叫标准差，正态分布常用来表示。

当=0，=1时，称服从标准正态分布，这时的总体叫标准正态总体。

叫标准正态曲线。

正态曲线xR的有关性质：(1)曲线在x轴上方，与x轴永不相交;(2)曲线关于直线x=对称，且在x=两旁延伸时无限接近x 轴;(3)曲线在x=处达到最高点;(4)当一定时，曲线形状由的大小来决定，越大，曲线越矮胖，表示总体分布比较离散，越小，曲线越瘦高，表示总体分布比较集中。

在标准正态总体N(0，1)中：高中数学关于正态分布知识总结【2】二项分布：一般地，在n次独立重复的试验中，用X表示事件A发生的次数，设每次试验中事件A发生的概率为p，则k=0，1，2，n，此时称随机变量X服从二项分布，记作X~B(n，p)，并记独立重复试验：(1)独立重复试验的意义：做n次试验，如果它们是完全同样的一个试验的重复，且它们相互独立，那么这类试验叫做独立重复试验.(2)一般地，在n次独立重复试验中，设事件A发生的次数为X，在每件试验中事件A发生的概率为p，那么在n次独立重复试验中，事件A恰好发生k次的概率为此时称随机变量X服从二项分布，记作并称p为成功概率.(3)独立重复试验：若n次重复试验中，每次试验结果的概率都不依赖于其他各次试验的结果，则称这n次试验是独立的.(4)独立重复试验概率公式的特点：是n次独立重复试验中某事件A恰好发生k次的概率.其中，n是重复试验的次数，p是一次试验中某事件A发生的概率，k是在n次独立重复试验中事件A恰好发生的次数，需要弄清公式中n，p，k的意义，才能正确运用公式.二项分布的判断与应用：(1)二项分布，实际是对n次独立重复试验从概率分布的角度作出的阐述，判断二项分布，关键是看某一事件是否是进行n 次独立重复试验，且每次试验只有两种结果，如果不满足这两个条件，随机变量就不服从二项分布.(2)当随机变量的总体很大且抽取的样本容量相对于总体来说又比较小，而每次抽取时又只有两种试验结果时，我们可以把它看作独立重复试验，利用二项分布求其分布列.求独立重复试验的概率：(1)在n次独立重复试验中，在相同条件下等价于各次试验的结果不会受其他试验的影响，即2，，n)是第i次试验的结果.(2)独立重复试验是相互独立事件的特例，只要有恰好恰有字样的用独立重复试验的概率公式计算更简单，要弄清n，p，k 的意义。

正态分布标准表
正态分布标准表是一种用于表示正态分布概率分布的表格，其中标准正态分布是其中的一种特例。

标准正态分布的概率密度函数为：
f(x) = 1/√(2π) * exp(-x^2/2)
其中，x是随机变量，π是圆周率，e是自然对数的底数。

在标准正态分布中，平均值为0，标准差为1。

标准正态分布表通常用于快速查找和计算正态分布下的概率值。

在表中，横轴表示标准正态分布下的取值范围，纵轴表示对应的概率值。

根据需要查找的x值，可以在表中查找到对应的概率值。

例如，如果需要查找z=1时的概率值，可以在标准正态分布表中查找到z=1对应的概率值。

由于标准正态分布中，z值是x值与平均值之差除以标准差得到的，因此当z=1时，对应的x值大约为1个标准差的位置。

在标准正φ(x)表中可以查找到此时的概率值为0.8413。

正态分布曲线的特点及曲线所表示的意义1．正态分布曲线的特点及曲线所表示的意义【知识点的知识】1．正态曲线及性质（1）正态曲线的定义函数φμ，σ（x）=2―(푥―휇)12휎2 ，x∈（﹣∞，+∞），其中实数μ和σ（σ＞0）为参数，我们称φ2휋휎푒μ，σ（x）的图象（如图）为正态分布密度曲线，简称正态曲线．（2）正态曲线的解析式①指数的自变量是x 定义域是R，即x∈（﹣∞，+∞）．②解析式中含有两个常数：π和e，这是两个无理数．③解析式中含有两个参数：μ和σ，其中μ可取任意实数，σ＞0 这是正态分布的两个特征数．④解析式前面有一个系数为1，后面是一个以e 为底数的指数函数的形式，幂指数为―2휋휎(푥―휇)22휎2．2．正态分布（1）正态分布的定义及表示푏如果对于任何实数a，b（a＜b），随机变量X 满足P（a＜X≤b）= φμ，σ（x）dx，则称X 的分布为正态分布，푎记作N（μ，σ2）．（2）正态总体在三个特殊区间内取值的概率值①P（μ﹣σ＜X≤μ+σ）＝0.6826；②P（μ﹣2σ＜X≤μ+2σ）＝0.9544；③P（μ﹣3σ＜X≤μ+3σ）＝0.9974．3．正态曲线的性质1/ 6正态曲线φμ，σ（x）=2―(푥―휇)12휎2，x∈R 有以下性质：2휋휎푒（1）曲线位于x 轴上方，与x 轴不相交；（2）曲线是单峰的，它关于直线x＝μ对称；（3）曲线在x＝μ处达到峰值1；2휋휎（4）曲线与x 轴围成的图形的面积为 1；（5）当σ一定时，曲线随着μ的变化而沿x 轴平移；（6）当μ一定时，曲线的形状由σ确定，σ越小，曲线越“瘦高”，表示总体的分布越集中；σ越大，曲线越“矮胖”，表示总体的分布越分散．4．三个邻域会用正态总体在三个特殊区间内取值的概率值结合正态曲线求随机变量的概率．落在三个邻域之外是小概率事件，这也是对产品进行质量检测的理论依据．【典型例题分析】题型一：概率密度曲线基础考察典例 1：设有一正态总体，它的概率密度曲线是函数f（x）的图象，且f（x）=21―(푥―10)8휋푒8，则这个正态总体的平均数与标准差分别是（）A．10 与 8 B．10 与 2 C．8 与 10 D．2 与 10解析：由21―(푥―10)8휋푒8=2―(푥―휇)12휎2，可知σ＝2，μ＝10．2휋휎푒答案：B．典例 2：已知随机变量ξ服从正态分布N（2，σ2），且P（ξ＜4）＝0.8，则P（0＜ξ＜2）等于（）A．0.6 B．0.4 C．0.3 D．0.22/ 6解析：由P（ξ＜4）＝0.8 知P（ξ＞4）＝P（ξ＜0）＝0.2，故P（0＜ξ＜2）＝0.3．故选C．典例 3：已知随机变量X 服从正态分布N（3，1），且P（2≤X≤4）＝0.682 6，则P（X＞4）等于（）A．0.158 8 B．0.158 7 C．0.158 6 D．0.158 51解析由正态曲线性质知，其图象关于直线x＝3 对称，∴P（X＞4）＝0.5﹣2P（2≤X≤4）＝0.5 ―12× 0.682 6＝0.1587．故选B．题型二：正态曲线的性质1典例 1：若一个正态分布的概率密度函数是一个偶函数，且该函数的最大值为．42휋（1）求该正态分布的概率密度函数的解析式；（2）求正态总体在（﹣4，4]的概率．分析：要确定一个正态分布的概率密度函数的解析式，关键是求解析式中的两个参数μ，σ的值，其中μ决定曲线的对称轴的位置，σ则与曲线的形状和最大值有关．解（1）由于该正态分布的概率密度函数是一个偶函数，所以其图象关于y 轴对称，即μ＝0．由12휋휎=1，42휋得σ＝4，故该正态分布的概率密度函数的解析式是φμ，σ（x）=21―푥42휋푒32，x∈（﹣∞，+∞）．（2）P（﹣4＜X≤4）＝P（0﹣4＜X≤0+4）＝P（μ﹣σ＜X≤μ+σ）＝0.6826．点评：解决此类问题的关键是正确理解函数解析式与正态曲线的关系，掌握函数解析式中参数的取值变化对曲线的影响．3/ 6典例 2：设两个正态分布N（μ1，휎12）（σ1＞0）和N（μ2，휎22）（σ2＞0）的密度函数图象如图所示，则有（）A．μ1＜μ2，σ1＜σ2B．μ1＜μ2，σ1＞σ2C．μ1＞μ2，σ1＜σ2D．μ1＞μ2，σ1＞σ2解析：根据正态分布N（μ，σ2）函数的性质：正态分布曲线是一条关于直线x＝μ对称，在x＝μ处取得最大值的连续钟形曲线；σ越大，曲线的最高点越低且较平缓；反过来，σ越小，曲线的最高点越高且较陡峭，故选A．答案：A．题型三：服从正态分布的概率计算典例 1：设X～N（1，22），试求（1）P（﹣1＜X≤3）；（2）P（3＜X≤5）；（3）P（X≥5）．分析：将所求概率转化到（μ﹣σ，μ+σ]．（μ﹣2σ，μ+2σ]或[μ﹣3σ，μ+3σ]上的概率，并利用正态密度曲线的对称性求解．解析：∵X～N（1，22），∴μ＝1，σ＝2．（1）P（﹣1＜X≤3）＝P（1﹣2＜X≤1+2）＝P（μ﹣σ＜X≤μ+σ）＝0.682 6．（2）∵P（3＜X≤5）＝P（﹣3＜X≤﹣1），∴P（3＜X≤5）=12[P（﹣3＜X≤5）﹣P（﹣1＜X≤3）]4/ 6=12[P（1﹣4＜X≤1+4）﹣P（1﹣2＜X≤1+2）]=12[P（μ﹣2σ＜X≤μ+2σ）﹣P（μ﹣σ＜X≤μ+σ）]=12×（0.954 4﹣0.682 6）＝0.1359．（3）∵P（X≥5）＝P（X≤﹣3），∴P（X≥5）=12[1﹣P（﹣3＜X≤5）]=12[1﹣P（1﹣4＜X≤1+4）]=12[1﹣P（μ﹣2σ＜X≤μ+2σ）]=12×（1﹣0.954 4）＝0.0228．求服从正态分布的随机变量在某个区间取值的概率，只需借助正态曲线的性质，把所求问题转化为已知概率的三个区间上．典例 2：随机变量ξ服从正态分布N（1，σ2），已知P（ξ＜0）＝0.3，则P（ξ＜2）＝．解析：由题意可知，正态分布的图象关于直线x＝1 对称，所以P（ξ＞2）＝P（ξ＜0）＝0.3，P（ξ＜2）＝1﹣0.3＝0.7．答案：0.7．题型 4：正态分布的应用典例 1：2011 年中国汽车销售量达到 1 700 万辆，汽车耗油量对汽车的销售有着非常重要的影响，各个汽车制造企业积极采用新技术降低耗油量，某汽车制造公司为调查某种型号的汽车的耗油情况，共抽查了 1 200 名车主，据统计该种型号的汽车的平均耗油为百公里 8.0 升，并且汽车的耗油量ξ服从正态分布N（8，σ2），已知耗油量ξ∈[7，9]的概率为 0.7，那么耗油量大于 9 升的汽车大约有辆．解析：由题意可知ξ～N（8，σ2），故正态分布曲线以μ＝8 为对称轴，又因为P（7≤ξ≤9）＝0.7，故P（7≤ξ≤9）＝2P（8≤ξ≤9）＝0.7，所以P（8≤ξ≤9）＝0.35，而P（ξ≥8）＝0.5，所以P（ξ＞9）＝0.15，故耗油量大于 9 升的汽车大约有 1 200×0.15＝180 辆．5/ 6点评：服从正态分布的随机变量在一个区间上的概率就是这个区间上，正态密度曲线和x 轴之间的曲边梯形的面푥1+푥2积，根据正态密度曲线的对称性，当P（ξ＞x1）＝P（ξ＜x2）时必然有2=μ，这是解决正态分布类试题的一个重要结论．1典例 2：工厂制造的某机械零件尺寸X 服从正态分布N（4，），问在一次正常的试验中，取 1 000 个零件时，不9属于区间（3，5]这个尺寸范围的零件大约有多少个？1解∵X～N（4，），∴μ＝4，σ=91 3．∴不属于区间（3，5]的概率为P（X≤3）+P（X＞5）＝1﹣P（3＜X≤5）＝1﹣P（4﹣1＜X≤4+1）＝1﹣P（μ﹣3σ＜X≤μ+3σ）＝1﹣0.9974＝0.0026≈0.003，∴1 000×0.003＝3（个），即不属于区间（3，5]这个尺寸范围的零件大约有 3 个．【解题方法点拨】正态分布是高中阶段唯一连续型随机变量的分布，这个考点虽然不是高考的重点，但在近几年新课标高考中多次出现，其中数值计算是考查的一个热点，考生往往不注意对这些数值的记忆而导致解题无从下手或计算错误．对正态分布N（μ，σ2）中两个参数对应的数值及其意义应该理解透彻并记住，且注意第二个数值应该为σ2而不是σ，同时，记住正态密度曲线的六条性质．6/ 6。