六年级数学上册找规律题

一、等差型数列规律1.有一组数：7，12，17，22，27，…请观察这组数的构成规律，用你发现的规律确定 第8个数为 , 第n 个数为 ． 二、等比型数列规律2. 有一组数：1，4，16，64，……，请观察这组数的构成规律，用你发现的规律确定三、含n 2型数列规律3.有一组数：2，6，12，20，30，…请观察这组数的构成规律，用你发现的规律 确定第8个数为 , 第n 个数为 ．四、其它数列规律列举4.观察下列一组数：32，54，76，98，1110，…… ，它们是按一定规律排列的，那么这一组数的 第k 个数是五、循环型数列.5. 已知221=，422=，32=8，42=16，25=32，……观察上面规律，试猜想20082 的末位数是 .6. 若1113a =-，2111a a =-，3211a a =-，… ；则2014a 的值为 ． 六、算式型规律7. 已知22223322333388+=⨯+=⨯，，244441515+=⨯，……，若288a a b b+=⨯（a 、b 为正整数）则a b += ．8. 研究下列算式，你会发现什么规律？1×3+1=22； 2×4+1=32； 3×5+1=42； 4×6+1=52 …………，（1） 请用含n 的式子表示你发现的规律：___________________.（2） 请你用发现的规律解决下面问题计算11111(1)(1)(1)(1)(1)132********+++++⨯⨯⨯⨯⨯的值七、数列阵型9.观察下列三行数： （课本P43页例4变式题）第一行：-1,2，-3,4，-5……第二行：1,4,9，16,25，……第三行：0,3,8,15,24，……(1)第一行数按什么规律排列？(2)第二行、第三行分别与第一行数有什么关系？(3)取每行的第10个数，计算这三个数的和．。

（小升初真题）六年级数学找规律题（易错题、难题）名师详解连载一第一关：我会找规律1.如下图，根据图形与数的规律，第10个数是（）。

2．九张卡片上分别写着1～9九个数字。

甲、乙、丙、丁四人玩数字游戏，每人拿两张。

如果结果是：甲的两张数字之和是9，乙的两张数字之差是6，丙的两张数字之积是12，丁的两张数字之商是3。

那么剩下的这张数字是（）。

3.六年级1、2、3、4四个班举行拔河比赛，甲、乙、丙三个同学猜测四个班比赛的前三名名次。

甲说：1班第三，3班第一；乙说：3班第二，2班第三；丙说：4班第二，1班第一。

比赛结果，三个人都猜对了一半。

那么，1班第（）名，4班第（）名。

4．按如右规律摆放三角形则第⑥个图三角形的个数为()。

A．15 B．17 C．20 D．245.下面的图形中，（）是正方体的表面展开图。

1.根据规律填空：61，21，（ ），29，227，（ ）。

2.海边灯塔上的一盏照明灯以固定的规律发出亮光。

下图表示前14秒灯光明暗变化的情况，第1秒亮（ ），第2秒暗（ ），第3秒暗（ ）……观察下图的变化规律，请你判断第39秒照明灯是（ ）的。

（填写“亮”或“暗”。

）3. 如下图所示，用白色和灰色小正方形按下图的规律摆大正方形。

照这样接着摆下去，第6幅图一共有（ ）个白色小正方形。

4.将同样大小的正方形按下列规律摆放,重叠部分涂上阴影,则下面图案中,第1个图案有3个正方形,第2个图案有7个正方形,那么:第1个 第2个 第3个(1)第六个图案中有（ ）个正方形;(2)若第n 个图案中有7999个正方形，则n=（ ）。

第二关：我会找规7. 31，91，271……按这组数的规律，第五个数应该是（ ）；如果这样一直写下去，那么这个数会越来越接近（ ）。

8. 学校阅览室有能坐4人的方桌,如果多于4人,就把方桌拼成一行,2张方桌拼成一行能坐6人(如图所示) ,请你结合这个规律算一算, 6张桌子拼成一行能坐（ ）人, n 张桌子拼成一行能坐（ ）人。

六年级数学找规律练习题班级姓名等级例 1 假设a#b=（a+b）+（a—b）；求13#5和13#（5#4）练习一1、将新运算定义为a＊b=（a+b）×（a—b）；求27＊92、设a＊b=a 2+2b；求10＊6和5＊（2＊8）13、设a＊b=3a—b×1；求（15＊24）＊（10＊12）2例 2 设p、q 是两个数；规定：p # q=4×q —（p+q）÷2；求 3 #（4# 6）练习二1、设p、q是两个数；规定：p # q=4×q—（p+q）÷2；求5#（6# 4）2、设p、q 是两个数；规定：p # q=p2+（p—q）×2；求30#（5# 3）3、设M 、N是两个数；规定：M # N=M N+M N1求—例 3 如果 1&5=1+11+111+1111+1111；1 2&4=2+22+222+2222；3&3=3+33+333；4&2=4+44 ； 那么 7&4= ；210&2= 。

练习三1、 如果 1&5=1+11+111+1111+1111；1 2&2=2+22 ；3&3=3+33+333 ⋯⋯ 那么 4&4=2、规定 a&b=a+aa+aaa+aaaa+a ⋯⋯ a （ b 个 a ）；那么 8&5= 。

1 1 13、如果 2&1= 1 ；3&2= 1 ；4&3= 1；那么（ 6&3）÷（2&6）=。

2 33 4441 例 4 设 a@b=4a —2b+ 1ab ；求 x@（4@1） =34 中的未知数 x练习四1、设 a@b=3a —2b ；已知 x@（4@1）=7；求 x3、对任意两个整数 x 和 y 定义新运算“ #”：x#y= 4xy（其中 m 是一个确定的整数） 。

找规律的练习题六年级一、填空题：1. 2，4，6，8，10，____2. 1，4，9，16，____3. 3，6，9，12，15，____4. 5，10，15，20，____5. 2，5，10，17，26，____二、选择题：1. 下列哪个数列是等差数列？A. 1，4，9，16，25B. 2，4，8，16，32C. 3，6，12，24，48D. 5，10，17，26，372. 下列哪个数列是等比数列？A. 1，4，9，16，25B. 2，4，8，16，32C. 3，6，12，24，48D. 5，10，20，40，80三、找规律题：1. 2，4，8，16，32，____2. 3，6，9，18，27，____3. 4，9，16，25，36，____4. 5，10，20，40，80，____5. 1，3，6，10，____四、编程题：请用程序打印出如下的数列：1. 1，2，3，4，5，6，7，8，9，102. 2，4，6，8，10，12，14，16，18，203. 3，6，9，12，15，18，21，24，27，304. 4，8，12，16，20，24，28，32，36，405. 5，10，15，20，25，30，35，40，45，50以上是六年级找规律的练习题，请同学们根据题目提供的数列，找出规律，填写正确答案。

在选择题和填空题中，选择正确答案并写在题目后的横线上或者填写在对应的空格中。

对于找规律题，同学们可以通过观察数列中数字的变化，找出其中的规律并填写下一个数。

对于编程题，如果你会编程，可以尝试用程序打印出相应的数列。

如果不会编程，可以借助计算器或手动计算得出数列中的数字，并填写答案。

希望同学们能通过这些练习题提升自己找规律的能力，加深对数列规律的理解。

找规律不仅可以在数学上帮助我们解题，还可以培养我们的逻辑思维能力和观察力。

希望同学们能够积极参与，提高自己的数学水平。

以上就是六年级找规律的练习题。

六年级数学总复习--找规律练习题1.如图.摆1个三角形需要3根小棒.摆2个三角形需要5根小棒.摆3个三角形需要7根小棒….像这样连续摆10个三角形需要（）根小棒.摆n个三角形需要（）根小棒；有37根小棒可以摆个这样的三角形．2.如上图所示.用同样的火柴棒摆正方形.摆1个正方形需要（）根火柴棒.摆2个正方形需要（）根火柴棒…….如果摆100个正方形需要（）根火柴棒.摆n个正方形需要（）根小棒·3.用同样长的小棍摆成如图所示的图形.照这样继续摆.第⑥个图形用（）根小棍.第n个图形用（）根小棍·4.像如图这样摆下去.n个六边形需要（）小木棒.当n=20时.共用了（）根小木棒·5、摆六边形（如图）．（1）摆1个六边形需要（）根小棒.摆2个六边形需要（）根小棒.摆3个六边形需要（）根小棒·（2）照这样下去.摆n个六边形需要（）根小棒（用含有字母n的式子表示）.101根可以摆（）个六边形·5.用小棒按照如下方式摆图形．（1）摆1个八边形需要8根小棒.摆2个八边形需要（）根小棒.摆10个八边形需要（）根小棒·（2）如果想摆n个八边形.需要（）根小棒·（3）有2010根小棒.可以摆（）个这样的八边形·6.用小棒可摆成小鱼.摆要8根.摆要14根.摆要20根…像这样.当摆成10条小鱼连在一起的时.需要（）根小棒·7.如下图.用同样大小的黑色棋子按图所示的方式摆图案.按照这样的规律摆下去.第10个图案需棋子（）枚.第n个图案需棋子（）枚·8.用长度相等的小木棒按照下图的方式搭塔式三角形.按照这样的规律搭下去.搭第5个图形需要（）根小木棒.搭第m个图形需要（）根小木棒·9.猜猜用火柴棒摆出大小不同的长方形（如下图）．第1个长方形需要（）根火柴棒.第 2个长方形需要（）根小棒.如果按这样的规律摆下去.第10个长方形共需要（）根火柴棒·8、如图所示：用黑白两种颜色的正五边形地砖按下图所示的规律.拼成若干个蝴蝶图案.则第7幅蝴蝶图案中白色地砖有（）块．9、用黑白两种颜色的正六边形地面砖按如图所示的规律.拼成若干个图案.则第2012个图案中有白色地面砖（）块·10、用同样规格的黑白两种颜色的正方形.按如图方式拼图.如果继续铺下去.那么第n个图形要用（）块黑色正方形·。

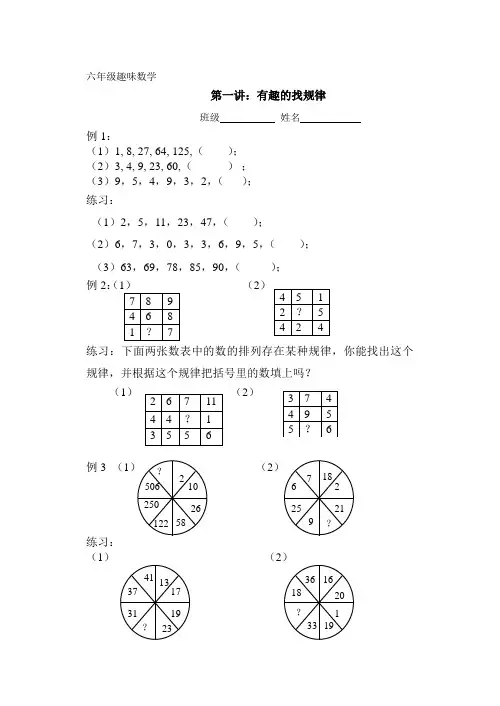
六年级趣味数学第一讲：有趣的找规律班级 姓名例1：（1）1, 8, 27, 64, 125,（ ）；（2）3, 4, 9, 23, 60,（ ） ；（3）9，5，4，9，3，2，（ ）；练习：（1）2，5，11，23，47，（ ）；（2）6，7，3，0，3，3，6，9，5，（ ）；（3）63，69，78，85，90，（ ）；例2：（（2） 练习：下面两张数表中的数的排列存在某种规律，你能找出这个规律，并根据这个规律把括号里的数填上吗？（1）（2）例3 （1（2练习：（1）（2）综合练习：1、找规律填数。

（1）2, 5, 10, 17, 28, （ ）,（ ）（2）94，46，22，10，（ ），（ ）（3）142857、428571、285714、857142、( )2、下图所示的图形中的数字都有各自的规律，先把规律找出来，再把空缺的数字填上：3. 下图所示的图形中的数字都有各自的规律，先把规律找出来，4、下图中，每个圆代表一个数码，每横行的三个圆从左到右看做一个三位数，四行表示的四个三位数是890， 784，361，256。

那么，5．下图的数之间存在着某种关系，请按照这一关系求出数a 和b 。

6 7 11 123 89 2 8 2 5 21 123 7 6 2 14 4 ？六年级趣味数学第二讲：有趣的数字谜班级姓名例1．从1～7中选出六个数字填入下式的□中，能得到的最大结果是多少？□×（□-□）÷□-□×□。

练习：1、从1～9这九个数字中选出八个填入下式的八个○内，使得算式的结果尽可能大：[○÷○×（○+○）]-[○×○+○-○]。

2、在下式的四个□内填入四个不同的一位数，要求左边的数比右边的数小，并且运算结果等于24。

□÷（□÷□÷□）=24。

例2、在下列各图中，分别从1～8中选择六个数字填入□内，使得按顺时针方向计算的各关系式成立：练习：将1～8这八个自然数填入左下图的空格中，使四边形组成的四个等式都成立。

六年级数学找规律练习题班级 姓名等级例 1 假设 a#b=（ a+b ） +（a —b ）；求 13#5 和 13#（5#4） 练习一1、将新运算定义为 a ＊b=（a+b ）×（a —b ）；求 27＊92、设 a ＊b=a 2 +2b ；求 10＊ 6 和 5＊（ 2＊8）3、设 a ＊b=3a —b ×1；求 (15＊ 24）＊（ 10 ＊12）2例 2 设 p 、q 是两个数；规定： p # q=4×q —（ p +q ）÷2；求 3 #（ 4# 6） 练习二1、设 p 、q 是两个数；规定： p # q=4×q —（ p +q ）÷2；求 5#（ 6# 4）2、设 p 、q 是两个数；规定： p # q=p 2 +（p —q ） ×2；求 30#（5# 3）、设 M 、 N 是两个数；规定：MN ；求 10#20—13M # N=+4N M例 3 如果 1&5=1+11+111+1111+11111；2&4=2+22+222+2222；3&3=3+33+333 ；4&2=4+44 ； 那么 7&4= ；210&2= 。

练习三1、如果 1&5=1+11+111+1111+11111； 2&2=2+22 ；3&3=3+33+333 ⋯⋯ 那么 4&4= 。

2、规定 a&b=a+aa+aaa+aaaa+a ⋯⋯ a （ b 个 a ）；那么 8&5= 。

、如果1 ；3&2= 1 ； 4&3=1；那么（ 6&3 ）÷（2&6 ）= 。

33 4442例 4 设 a@b=4a —2b+ 1ab ；求 x@（4@1） =34 中的未知数 x2练习四1、设 a@b=3a —2b ；已知 x@（4@1）=7；求 x、对两个整数 a 和 b 定义新运算“ & ”；a&b= 2a b ；求 6&4+9&82ba ba4xyx 和 y 定义新运算“ #”： x#y= （其中 m 是一个确定的整数） 。

1、观察下面的几个算式: 1+2+1=4, 1+2+3+2+1=9, 1+2+3+4+3+2+1=16, 1+2+3+4+5+4+3+2+仁25, •- 根据你所发现的规律，请你直接写出下面式子的结果:1+2+3+ • • +99+100+99+…+3+2+1 = 2、已知下列等式：3 .2=1 ；3 3 2+ 2 = 3 ;2 + 2 +3 =6 ;2+ 2 + 3 + 4 = 10 ;由此规律知，第⑤个等式是3、如图是用火柴棍摆成边长分别是1、2、3根火柴棍时的正方形,4、如图是五角星灯连续旋转闪烁所成的三个图形。

照此规律闪烁，下一个呈现出来的图形是班级姓名等级摆出的正方形所用的火柴棍的根数为S,则S= （用含n的代数式表示，n为正整数）.①②③④当边长为n根火柴棍时，若☆ ☆ ☆6、如图，在图1中，互不重叠的三角形共有 4个，在图2中，互不重叠的三角形共有 7个，在图3中，互不重叠的三角形共有 10个， ，则在第n 个图形中，互不重叠的三角形共有 个（用含n 的代数式表示）。

8、在计算机程序中，二杈树是一种表示数据结构的方法。

如图，一层二杈树的结点总数是 二层二杈树的结点总数是 3，三层二杈树的结点总数是 7,四层二杈树的结点总数是15……照此规律七层二杈树的结点总数是▲ A一层二杈树二层二杈树三层二杈树☆ ☆ ☆7、小的黑、白两种颜色的棋子摆设如下图所示的正方形图案，则第 n 个图案需要用白色棋子----------------- (oooc ooooooo 0*0 oooo ooooooon 的代数式表示）ooooo^ r1 ・rr J1,”需要火柴根。

12、如图，将第一个图（图①）所示的正三角形连结各边中点进行分割， 得到第二个图（图②）；再将第二个图中最中间的小正三角形按同样的方式进行分割，得到第三个图（图 ③）；再将第三个图中最中间的小正三角形按同样的方式进行分割，……，则得到的第五个图中， 共有 个正三角形。

六年级数学找规律练习题班级 姓名 等级例1 假设a#b=（a+b ）+（a —b ）；求13#5和13#（5#4）练习一1、将新运算定义为a ＊b=（a+b ）×（a —b ）；求27＊92、设a ＊b=a 2+2b ；求10＊6和5＊（2＊8）3、设a ＊b=3a —b ×21；求(15＊24）＊（10＊12）例2 设p 、q 是两个数；规定：p # q=4×q —（p +q ）÷2；求3 #（4# 6）练习二1、设p 、q 是两个数；规定：p # q=4×q —（p +q ）÷2；求5#（6# 4）2、设p 、q 是两个数；规定：p # q=p 2+（p —q ）×2；求30#（5# 3）3、设M 、N 是两个数；规定：M # N=N M +MN ；求10#20—41例3如果1&5=1+11+111+1111+11111；2&4=2+22+222+2222；3&3=3+33+333；4&2=4+44；那么7&4= ；210&2= 。

练习三1、如果1&5=1+11+111+1111+11111；2&2=2+22；3&3=3+33+333……那么4&4= 。

2、规定a&b=a+aa+aaa+aaaa+a ……a （b 个a ）；那么8&5= 。

3、如果2&1=21；3&2=331；4&3=4441；那么（6&3）÷（2&6）= 。

例4 设a@b=4a —2b+21ab ；求x@（4@1）=34中的未知数x练习四1、设a@b=3a —2b ；已知x@（4@1）=7；求x2、对两个整数a 和b 定义新运算“&”；a&b=()()b a b a ba -⨯+-2；求6&4+9&83、对任意两个整数x 和y 定义新运算“#”：x#y=ymx xy34+（其中m 是一个确定的整数）。

六年级上册数学找规律题一、数字规律类。

1. 观察数列：1，3，5，7，9，…，第n个数是多少？解析：这是一个奇数数列，相邻两个数的差都是2。

第一个数是1 = 2×1 1，第二个数是3=2×2 1，第三个数是5 = 2×3 1，以此类推，第n个数是2n 1。

2. 数列：2，4，8，16，32，…，第n个数是多少？解析：这个数列中，后一个数都是前一个数的2倍。

第一个数是2 = 2^1，第二个数是4 = 2^2，第三个数是8 = 2^3，所以第n个数是2^n。

3. 1，4，9，16，25，…，第n个数是多少？解析：这些数分别是1²，2²，3²，4²，5²，…，所以第n个数是n²。

4. 数列：1， 1，1， 1，1，…，第n个数是多少？解析：这个数列是正负交替的，当n为奇数时，数为1；当n为偶数时，数为1。

所以第n个数是(-1)^(n + 1)。

5. 2，5，10，17，26，…，第n个数是多少？解析：这个数列中，第一个数2=1² + 1，第二个数5 = 2²+1，第三个数10 = 3² + 1，第四个数17 = 4²+1，所以第n个数是n²+1。

6. 0，3，8，15，24，…，第n个数是多少？解析：这些数分别是1² 1，2² 1，3² 1，4² 1，5² 1，所以第n个数是n²1。

7. 1，1，2，3，5，8，13，…，求第n个数（斐波那契数列）。

解析：从第三项起，每一项都等于前两项之和。

设这个数列的第n项为F(n)，则F(n)=F(n 1)+F(n 2)（n≥3），F(1)=1，F(2)=1。

8. 数列：3，6，9，12，15，…，第100个数是多少？解析：这个数列是一个公差为3的等差数列，首项是3。

小学六年级数学找规律专项练习题，孩子提高必备！经典例题例1：找规律填数。

（1）1，3，5，7，（），（）。

（2）65，60，55，50，（），（）。

（3）1，10，100，1000，（），（）。

（4）1，2，4，7，11，（），（）。

（5）1，2，4，8，（），（）。

（6）1，3，4，7，11，（），（），（）。

思路点拨第（1）题，从左往右依次增加；第（2）题从左往右依次减少；第（3）题，从左往右依次在末尾添加一个，或者说依次乘；第（4）题从左往右，相邻两个数相差1,2,3,4……第（5）题中，1×2＝2,2×2＝4,4×2＝8，所以，8×2＝……第（6）题中，从第三个数开始，每个数都等于前面两个数的和。

模仿练习找规律填数。

（1）2，4，6，8，（），（）。

（2）1，5，9，13，（），（）。

（3）2，20，200，2000，（），（）。

（4）1，2，2，4，3，6，4，8，（），（）。

（5）49，42，35，（），（），（）。

（6）4，6，9，13，（），24，（）。

（7）100，81，64，（），36，25，（），9，4，1例2：仔细观察下列组图，在每一组的“？”处填上合适的数。

（1）（2）（3）（4）（5）思路点拨第（1）题中，3＋4＋8＝15；第（2）题中，2×3＋1＝7；第（3）题中，3×4＋5＝17；第（4）题中4×5－5＝20；第（5）题中，5＋3＋7＝15,15＋15＝30。

模仿练习仔细观察每组图的规律，在空白处填合适的数。

（1）（2）例3：根据下表中的排列规律，在空格里填上适当的数。

思路点拨分析表格中的数可以发现，按行看，12＋6＝18,8＋7＝15，也就是说每一行中间的数等于两边的两个数的和。

依此规律可以填出空格中的数。

找规律练习题1．按照下面所绘图形的排列规律，第25个图形是________．（画出草图）□△○△□△○△□△○△……2．仔细观察下面的图，想一想，第3幅图问号处应填什么图形？3．仔细观察下面的图形，想一想，第4幅图应画怎样的图形？4．根据下面前三幅图的变化规律，在第4幅图中画出阴影部分．5．想一想，方框内应有多少个小圆点？6．按照图形的变化规律，在“？”处画出相符的图形．7．观察图的排列规律，在“？”处填上恰当的图形．8．下面哪个图形和其他几个图形不一样，找出来，并打上“√”．9．观察下列黑白小球的排列规律，然后回答方框内有几个白球，几个黑球？10．四个小动物排座位，如下图：一开始，小老鼠坐在第1号，小猴子坐第2号，小兔坐第3号，小猫坐第4号．以后它们多次地交换位子：第一次上下两排交换，第二次（在第一次交换之后）左右两列交换，第三次上下两排交换，第四次左右两列交换，……这样换下去，问：第十次交换后，小兔子坐在第几号位子上？答案解析1．□提示：在这列图形中出现的图形有：正方形、三角形、圆，且三种图形出现的规律是：按照正方形→三角形→圆→三角形的顺序4个一组循环出现．因25÷4＝6……1，所以横线上应填第一个图形，即正方形．2．☆△提示：观察前两组图形可知，第一、二组都是由□○☆△组成，但顺序不同．第一组中的左边两个，在第二组中变为右边两个，而另外三个按原来的顺序移到了最左边．按此规律，“？”处应分别填上“☆”“△”．3．提示：观察前三幅图，大圆内都是■○△◇组成的，第一幅图中的图形按逆时针方向旋转可得到第二幅图形，第二幅图形按逆时针方向旋转可得到第三幅图形，同理可推得第四幅图形．4．提示：第一幅图的阴影部分均按顺时针方向旋转一格便可得到第二幅图，第二幅图中的阴影部分均按顺时针方向旋转一格便可得到第三幅图，由此，第三幅图中的阴影部分均按顺时针方向旋转一格便可得到第四幅图．5．方框内应填25个圆点．6．提示：观察前三幅图可知，前一幅图按逆时针方向旋转一格便可得到下一幅图．7．△提示：通过观察可知，从上到下每一横行圆的个数逐次减少1，三角的个数逐次增加1，由此推得“？”处的图形．8．（1）提示：图中的几何图形的共同特点是在图形内部都有一个同一类型的图形．但1、3、4、5内部的图形都较小，只有2内部图形较大，且位置和其它几个图形不同．（2）提示：这五幅图形都是由相同的两个图形重叠而成的，但不同的是前四个图形都是下面的图形盖住了上面的图形，只有5不同，是上面的图形盖住了下面的图形．9．9个白球，3个黑球．提示：观察图形可知，黑、白小球按照2个黑球，1个白球，2个黑球，3个白球，2个黑球，5个白球……的规律排列，即每组都是先有2个黑球，白球的个数每次增加2．10．小兔坐在第2号位置上．提示：小兔子开始在第3号位置上，第四次交换后，小兔子又回到原位，因10÷4＝2……2，所以小兔第十次交换后应与第二次交换后的位置相同．。

找规律专题一．解答题（共30小题）1．（2015•深圳）在生活中，经常把一些同样大小的圆柱管如图捆扎起来，下面我们来探索捆扎时绳子的长度，图中，每个圆的直径都是8厘米，当圆柱管放置放式是“单层平放”时，捆扎后的横截面积如图所示：那么，当圆柱管有100个时需要绳子厘米（π取3）2．（2015•龙泉驿区校级三模）摆一个六边形需要六根小棒，摆2个六边形需要11根小棒，3个需要16根小棒…问：摆10个六边形需要根小棒，摆100个六边形需要根小棒，摆n个六边形需要根小棒．3．（2015春•淮安校级期中）用计算器计算，再根据规律编写一道算式并直接写出得数．（24+25）×5=；（872+873）×5=；（2830+2831）×5=；（+）×=．4．（2015春•射阳县校级期中）根据规律填数．9×9+9=90 9876×9+6=8889098×9+8=890 98765×9+5=987×9+7=8890 987654×9+4=．5．（2015春•成都校级期中）如图表示“宝塔”，它们的层数不同，但都是由一样大的小三角形摆成的．仔细观察后，请回答：（1）五层的“宝塔”最下层包含多少个小三角形？六层呢？七层呢？n层呢？（2）整个五层“宝塔”一共包含多少个小三角形？六层呢？七层呢？n层呢？6．（2015春•西安校级期中）仔细观察，根据发现的规律把表格填完整．第几幅图 1 2 3 5 …n共几个面在外面…7．（2015春•盐城校级期中）用小棒如图的方式搭正方形．搭1个正方形要4根小棒，搭2个正方形要7根小棒．（1）搭3个正方形要根小棒；（2）搭8个正方形要根小棒；8．（2015春•团风县期中）一串珠子按照3颗黑珠，2颗白珠，3颗红珠，2颗蓝珠的顺序排列．（1）第14颗珠子是珠子．（2）第998颗珠子是颜色珠子．9．（2015春•射阳县校级期中）想一想，填一填．用上面的图形在左边表里框出5个数，先算出这5个数的和，再想想算出的和与中间一个数有什么关系？如果5个数的和为795，请在上面图形里写出这5个数．10．（2015春•威宁县校级期中）表中一共有50个奇数，黑线框出的5个数之和是115；仔细观察后回答问题．（1）你能发现每次框出的5个数的和与中间数有什么关系吗？（2）如果框出5个数的和要是375，应该怎么框？（先在图中框一框，并在下面用文字说明）（3）能框出和是295的5个数吗？为什么？（4）一共可以框出多少个大小不同的和？11．（2015春•株洲校级月考）不计算，运用规律在横线上填上合适的数．7×9=6377×9=693777×9=69937777×9=69993…777777777×9=1÷7=0.142857142857…2÷7=0.285714285714…3÷7=0.428571428571…4÷7=0.575÷7=0.76÷7=7÷7=12．（2014•涟水县模拟）观察与计算．计算：1+2+3+…+99+100+99+98+…+3+2+1=13．（2014•金寨县校级模拟）找规律，填表．序号①②③④⑤…⑩数列A 1 3 5 7 9 …数列B 0 1 4 9 (81)14．（2014•宝安区校级模拟）观察下面3题的规律，然后算出（1）（2）两小题的结果．1+2+1=2×2=41+2+3+2+1=3×3=91+2+3+4+3+2+1=16（1）1+2+3+…+99+100+99+…+3+2+1=（2）+++…+++1+++…+++=15．（2014•绍兴）有些题目可以通过观察找出规律，知道答案．按照下图算式的规律不变，如果商是123456，括号中的“减数”应该是．（3﹣3）÷27=0（33﹣6）÷27=1（333﹣9）÷27=12（3333﹣12）÷27÷=123．16．（2014•武平县）观察图形找规律：（1）按照图形变化规律填表：1 2 3 4 5 …正方形个数直角三角0 4 8 …形个数（2）如果画8个正方形能得到个直角三角形，画n个正方形能得到个直角三角形．17．（2014•东莞）探寻规律．如图 是一块瓷砖的图案，用这种瓷砖来铺设地面．如果铺成一个2×2的正方形图案（如图‚），其中完整的圆共有5个，如果铺成一个3×3的正方形图案（如图ƒ），其中完整的圆共有13个，如果铺成一个4×4的正方形图案（如图④），其中完整的圆共有25个．若这样铺成一个10×10的正方形图案，则其中完整的圆共有个．18．（2014•东台市）准备（1）每个都是棱长为1厘米的正方体．（2）一个挨着一个排成一排你要研究的问题是：正方体个数与拼成的长方体表面积之间的关系．探索过程：根据你的发现填空．当正方体个数为10时，所拼成的长方体表面积是平方厘米．当正方体个数为a时，所拼成的长方体表面积是平方厘米．当拼成的长方体表面积是202平方厘米时，正方体个数是．19．（2014•长沙）在如图所示的数表中，第100行左边的第一个数是．20．（2014•成都）有甲、乙两个同样的杯子，甲杯装满水，乙杯是空的．第一次将甲杯里的倒入乙杯，第二次将乙杯中水的倒回甲杯，第三次将甲杯中的倒回乙杯，第四次将乙杯中的倒回甲杯，…，这样反复倒2015 次后，甲杯中的水是原来的几分之几？21．（2014•陕西校级模拟）有一列数2，9，8，2，6，…从第3个数起，每个数都是前面两个数乘积的个位数字．例如第四个数就是第二、第三两数乘积9×8=72的个位数字2．问这一列数第1997个数是几？22．（2014•江油市校级模拟）有一串数，，，，，，，，，，…则是第个分数．23．（2014•临夏县模拟）找规律填数．1，4，9，16，，，49，，81．24．（2014•湖南模拟）分析推理找规律①1+2+1=4②1+2+3+2+1=9③1+2+3+4+3+2+1=16④1+2+…+49+50+49+…+2+1=⑤1+2+…+（n﹣1）+n+（n﹣1）+…+2+1=（n为自然数）25．（2014•江油市校级模拟）1+3=4=22，1+3+5=9=32，1+3+5+7=16=42，…1+3+5+…+（2n ﹣1）=20132，则n=．26．（2014•宁远县校级模拟）如图，第6个图形一共由个小三角形组成，第n 个图形，一共由个小角形组成．27．（2014•广州模拟）为了美化城市，某商场在门前的空地上用花盆按如图所示的方式搭正方形．（1）填写下表正方形的层数 1 2 3 4 5该层所需花盆的个数 4 12（2）按这种规律搭下去，搭第n（n为正整数）层正方形，需要盆花．28．（2014•台湾模拟）如图所示，按一定规律用棉花棒摆放图案：第一组的图案用棉花棒2枝，第二组用棉花棒7枝，第三组用棉花棒15枝，如此类推，问第二十组的图案用棉花棒多少枝﹖29．（2014•成都校级模拟）下面的小点按如图所示的规律摆放：第1个图形有6个小点，第2个图形有10个小点，第3个图形有16个小点，第4个图形有24个点…，依次规律，第10个图形中点的个数是30．（2014•海安县模拟）用小棒按照如下的方式摆图形．摆1个八边形需要8根小棒，摆2个八边形需要15根小棒，…摆50个八边形需要根小棒；如果摆这样的八边形用了771根小棒，你知道摆了个八边形．。

分数找规律的数学题六年级一、分数找规律题目。

1. 观察下面的分数序列：(1)/(2)，(2)/(3)，(3)/(4)，(4)/(5)，（），(6)/(7)。

- 解析：观察这些分数，发现分子依次是1、2、3、4……，分母依次是2、3、4、5……，所以括号里的分数分子应该是5，分母应该是6，答案是(5)/(6)。

2. 按规律填数：(1)/(3)，(3)/(6)，(5)/(9)，(7)/(12)，（）。

- 解析：分子的规律是依次加2，1，3，5，7……，分母的规律是依次加3，3，6，9，12……，所以下一个分数的分子是7 + 2=9，分母是12+ 3 = 15，答案是(9)/(15)。

3. 找出规律，填写分数：(2)/(5)，(4)/(10)，(8)/(20)，(16)/(40)，（）。

- 解析：分子依次是2，2×2 = 4，4×2=8，8×2 = 16，后一个分子是前一个分子的2倍；分母依次是5，5×2 = 10，10×2 = 20，20×2=40，后一个分母是前一个分母的2倍。

所以下一个分数分子是16×2=32，分母是40×2 = 80，答案是(32)/(80)。

4. 观察分数列：(1)/(4)，(3)/(8)，(5)/(12)，(7)/(16)，（）。

- 解析：分子是连续的奇数，1，3，5，7……，下一个奇数是9；分母是依次加4，4，8，12，16……，下一个分母是16 + 4=20，答案是(9)/(20)。

5. 按规律填空：(3)/(7)，(6)/(14)，(9)/(21)，(12)/(28)，（）。

- 解析：分子依次是3的倍数，3×1 = 3，3×2 = 6，3×3=9，3×4 = 12，下一个分子是3×5 = 15；分母依次是7的倍数，7×1=7，7×2 = 14，7×3 = 21，7×4=28，下一个分母是7×5 = 35，答案是(15)/(35)。

找规律训练1、 小马利用计算机设计了一个计算程序,输入和输出的数据如下表：请问：当小马输入数据8时,输出的数据是A ．618B ．638C ．658D ．678 2、观察下列数据,按某种规律在横线上填上适当的数：1,43-,95,167-,259, ,……3、“”是规定的一种运算法则:ab=a 2－2b.那么23的值为.若-3x=7,那么x= ;4、小明在做数学题时,发现下面有趣的结果：3-2=18+7-6-5=415+14+13-12-11-10=924+23+22+21-20-19-18-17=16… 根据以上规律可知第100行左起第一个数是_______.5、下面由火柴棒拼出的一列图形中,第n 个图形由n 个正方形组成,通过观察可以发现：1第4个图形中火柴棒的根数是 ；2第n 个图形中火柴棒的根数是 ．6、用黑白两种颜色的正六边形地面砖按如下所示的规律拼成若干个图案：则第4个图案中有白色地面砖________块；第n 个图案中有白色地面砖_________块.7、如图所示,已知等边三角形ABC 的边长为1,按图中所示的规律,用2010个这样的三角形镶嵌而成的四边形的周长是n =1 n =2 n =3 n=48、用同样大小的黑色棋子按图所示的方式摆图案,按照这样的规律摆下去,第21个图案需要棋子枚;9、7分一张长方形桌子可坐6人,按下图方式讲桌子拼在一起;12张桌子拼在一起可坐______人;3张桌子拼在一起可坐____人,n张桌子拼在一起可坐______人;（2）一家餐厅有40张这样的长方形桌子,按照上图方式每5张桌子拼成1张大桌子,则40张桌子可拼成8张大桌子,共可坐______人;10、如图所示,将多边形分割成三角形．图1中可分割出2个三角形；图2中可分割出3个三角形；图3中可分割出4个三角形；由此你能猜测出,n边形可以分割出_________个三角形;一个多边形,从它的某一个顶点出发,分别与其余各顶点连接,分割成18个三角形,那么这个多边形是边形;11、下图是由一些火柴棒搭成的图案．1摆第①个图案用根火柴棒,摆第②个图案用根火柴棒,摆第③个图案用根火柴棒;2按照这种方式摆下去,摆第n个图案用多少根火柴棒3计算一下摆121根火柴棒时,是第几个图案12、如图,线段AB 上的点数与线段的总数有如下关系：如果线段AB 上有三个点时,线段总共有3条,如果线段AB 上有4个点时,线段总数有6条,如果线段AB 上有5个点时,线段总数共有10条,……3=2+1 6=3+2+1 10=4+3+2+11当线段AB 上有10个点时,线段总数共有 条;2当线段AB 上有n 个点时,线段总数共有多少条13、某城市大剧院地面的一部分为扇形,观众席的座位按下列方式设置：按这种方式排下去,⑴ 5、6排各有多少个座位 4分⑵第n 排有多少个座位 6分14、我国著名的数学家华罗庚曾说过：“数形结合百般好,割裂分家万事非”,如图6-2,在边长为1的正方形纸板上,依次贴上面积为 21,41,81,…,n 21的长方形彩色纸片n 为大于1的整数,请你用“数形结合”的思想,依数形变化的规律,计算+++814121…+n 21=_________. 15、一列数：0,1,2,3,6,7,14,15,30．____,_____,____这串数是由小明按照一定规则写下来的,他第一次写下“0,1”,第二次按着写“2,3”,第三次接着写“6,7”第四次接着写“14,15”,就这样一直接着往下写,那么这串数的最后三个数应该是下面的A ．31,32,64B ．31,62,63C ．31,32,33D ．31,45,4616、计算91101415131412131-++-+-+- 17、观察下列计算211211-=⨯,3121321-=⨯,4131431-=⨯,5141541-=⨯…… 从计算结果中找规律,利用规律计算A CB ACD B A C DE B201320121541431321211⨯++⨯+⨯+⨯+⨯ 18．填在下面各正方形中的四个数之间都有相同的规律,根据此规律,m 的值是_________．1.已知一张桌子的价钱是一把椅子的10倍,又知一张桌子比一把椅子多288元,一张桌子和一把椅子各多少元解题思路：由已知条件可知,一张桌子比一把椅子多的288元,正好是一把椅子价钱的10-1倍,由此可求得一把椅子的价钱;再根据椅子的价钱,就可求得一张桌子的价钱;答题：解：一把椅子的价钱：288÷10-1=32元一张桌子的价钱：32×10=320元答：一张桌子320元,一把椅子32元;2. 3箱苹果重45千克;一箱梨比一箱苹果多5千克,3箱梨重多少千克 解题思路：可先求出3箱梨比3箱苹果多的重量,再加上3箱苹果的重量,就是3箱梨的重量;答题：解：45+5×3=45+15=60千克答：3箱梨重60千克;3. 甲乙二人从两地同时相对而行,经过4小时,在距离中点4千米处相遇;甲比乙速度快,甲每小时比乙快多少千米解题思路：根据在距离中点4千米处相遇和甲比乙速度快,可知甲比乙多走4×2千米,又知经过4小时相遇;即可求甲比乙每小时快多少千米;答题：解：4×2÷4=8÷4=2千米答：甲每小时比乙快2千米;4. 李军和张强付同样多的钱买了同一种铅笔,李军要了13支,张强要了7支,李军又给张强0.6元钱;每支铅笔多少钱解题思路：根据两人付同样多的钱买同一种铅笔和李军要了13支,张强要了7支,可知每人应该得13+7÷2支,而李军要了13支比应得的多了3支,因此又给张强0.6元钱,即可求每支铅笔的价钱;答题：解：0.6÷13-13+7÷2=0.6÷13—20÷2=0.6÷3=0.2元答：每支铅笔0.2元;5.甲乙两辆客车上午8时同时从两个车站出发,相向而行,经过一段时间,两车同时到达一条河的两岸;由于河上的桥正在维修,车辆禁止通行,两车需交换乘客,然后按原路返回各自出发的车站,到站时已是下午2点;甲车每小时行40千米,乙车每小时行45千米,两地相距多少千米交换乘客的时间略去不计解题思路：根据已知两车上午8时从两站出发,下午2点返回原车站,可求出两车所行驶的时间;根据两车的速度和行驶的时间可求两车行驶的总路程;答题：解：下午2点是14时;往返用的时间：14-8=6时两地间路程：40+45×6÷2=85×6÷2=255千米答：两地相距255千米;6. 学校组织两个课外兴趣小组去郊外活动;第一小组每小时走4.5千米,第二小组每小时行3.5千米;两组同时出发1小时后,第一小组停下来参观一个果园,用了1小时,再去追第二小组;多长时间能追上第二小组解题思路：第一小组停下来参观果园时间,第二小组多行了3.5-4.5-3.5 千米,也就是第一组要追赶的路程;又知第一组每小时比第二组快4.5-3.5千米,由此便可求出追赶的时间;答题：解：第一组追赶第二组的路程：3.5-4.5- 3.5=3.5-1=2.5千米第一组追赶第二组所用时间：2.5÷4.5-3.5=2.5÷1=2.5小时答：第一组2.5小时能追上第二小组;7. 有甲乙两个仓库,每个仓库平均储存粮食32.5吨;甲仓的存粮吨数比乙仓的4倍少5吨,甲、乙两仓各储存粮食多少吨解题思路：根据甲仓的存粮吨数比乙仓的4倍少5吨,可知甲仓的存粮如果增加5吨,它的存粮吨数就是乙仓的4倍,那样总存粮数也要增加5吨;若把乙仓存粮吨数看作1倍,总存粮吨数就是4+1倍,由此便可求出甲、乙两仓存粮吨数;答题：解：乙仓存粮：32.5×2+5÷4+1=65+5÷5=70÷5=14吨甲仓存粮：14×4-5=56-5=51吨答：甲仓存粮51吨,乙仓存粮14吨;8. 甲、乙两队共同修一条长400米的公路,甲队从东往西修4天,乙队从西往东修5天,正好修完,甲队比乙队每天多修10米;甲、乙两队每天共修多少米解题思路：根据甲队每天比乙队多修10米,可以这样考虑：如果把甲队修的4天看作和乙队4天修的同样多,那么总长度就减少4个10米,这时的长度相当于乙4+5天修的;由此可求出乙队每天修的米数,进而再求两队每天共修的米数;答题：解：乙每天修的米数：400-10×4÷4+5=400-40÷9=360÷9=40米甲乙两队每天共修的米数：40×2+10=80+10=90米答：两队每天修90米;9. 学校买来6张桌子和5把椅子共付455元,已知每张桌子比每把椅子贵30元,桌子和椅子的单价各是多少元解题思路：已知每张桌子比每把椅子贵30元,如果桌子的单价与椅子同样多,那么总价就应减少30×6元,这时的总价相当于6+5把椅子的价钱,由此可求每把椅子的单价,再求每张桌子的单价;答题：解：每把椅子的价钱：455-30×6÷6+5=455-180÷11=275÷11=25元每张桌子的价钱：25+30=55元答：每张桌子55元,每把椅子25元;10. 一列火车和一列慢车,同时分别从甲乙两地相对开出;快车每小时行75千米,慢车每小时行65千米,相遇时快车比慢车多行了40千米,甲乙两地相距多少千米解题思路：根据已知的两车的速度可求速度差,根据两车的速度差及快车比慢车多行的路程,可求出两车行驶的时间,进而求出甲乙两地的路程;答题：解：7+65×40÷75- 65=140×40÷10=140×4=560千米答：甲乙两地相距560千米;11. 某玻璃厂托运玻璃250箱,合同规定每箱运费20元,如果损坏一箱,不但不付运费还要赔偿100元;运后结算时,共付运费4400元;托运中损坏了多少箱玻璃解题思路：根据已知托运玻璃250箱,每箱运费20元,可求出应付运费总钱数;根据每损坏一箱,不但不付运费还要赔偿100元的条件可知,应付的钱数和实际付的钱数的差里有几个100+20元,就是损坏几箱;答题：解：20×250-4400÷10+20=600÷120=5箱答：损坏了5箱;12. 五年级一中队和二中队要到距学校20千米的地方去春游;第一中队步行每小时行4千米,第二中队骑自行车,每小时行12千米;第一中队先出发2小时后,第二中队再出发,第二中队出发后几小时才能追上一中队解题思路：因第一中队早出发2小时比第二中队先行4×2千米,而每小时第二中队比第一中队多行12-4千米,由此即可求第二中队追上第一中队的时间;答题：解：4×2÷12-4=4×2÷8 =1时答：第二中队1小时能追上第一中队;13. 某厂运来一堆煤,如果每天烧1500千克,比计划提前一天烧完,如果每天烧1000千克,将比计划多烧一天;这堆煤有多少千克解题思路：由已知条件可知道,前后烧煤总数量相差1500+1000千克,是由每天相差1500-1000千克造成的,由此可求出原计划烧的天数,进而再求出这堆煤的数量;答题：解：原计划烧煤天数：1500+1000÷1500-1000=2500÷500=5天这堆煤的重量：1500×5-1=1500×4=6000千克答：这堆煤有6000千克;14. 妈妈让小红去商店买5支铅笔和8个练习本,按价钱给小红3.8元钱;结果小红却买了8支铅笔和5本练习本,找回0.45元;求一支铅笔多少元解题思路：小红打算买的铅笔和本子总数与实际买的铅笔和本子总数量是相等的,找回0.45元,说明8-5支铅笔当作8-5本练习本计算,相差0.45元;由此可求练习本的单价比铅笔贵的钱数;从总钱数里去掉8个练习本比8支铅笔贵的钱数,剩余的则是5+8支铅笔的钱数;进而可求出每支铅笔的价钱;答题：解：每本练习本比每支铅笔贵的钱数：0.45÷8-5=0.45÷3=0.15元8个练习本比8支铅笔贵的钱数：0.15×8=1.2元每支铅笔的价钱：3.8-1.2÷5+8=2.6÷13=0.2元答：每支铅笔0.2元;15. 根据一辆客车比一辆卡车多载10人,可求6辆客车比6辆卡车多载的人数,即多用的8-6辆卡车所载的人数,进而可求每辆卡车载多少人和每辆大客车载多少人;解题思路：根据一辆客车比一辆卡车多载10人,可求6辆客车比6辆卡车多载的人数,即多用的8-6辆卡车所载的人数,进而可求每辆卡车载多少人和每辆大客车载多少人;答题：解：卡车的数量：360÷10×6÷8-6=360÷10×6÷2=360÷30=12辆客车的数量：360÷10×6÷8-6+10=360÷30+10=360÷40=9辆答：可用卡车12辆,客车9辆;16. 某筑路队承担了修一条公路的任务;原计划每天修720米,实际每天比原计划多修80米,这样实际修的差1200米就能提前3天完成;这条公路全长多少米解题思路：根据计划每天修720米,这样实际提前的长度是720×3-1200米;根据每天多修80米可求已修的天数,进而求公路的全长;答题：解：已修的天数：720×3-1200÷80=960÷80=12天公路全长：720+80×12+1200=800×12+1200=9600+1200=10800米答：这条公路全长10800米;17. 某鞋厂生产1800双鞋,把这些鞋分别装入12个纸箱和4个木箱;如果3个纸箱加2个木箱装的鞋同样多;每个纸箱和每个木箱各装鞋多少双解题思路：根据已知条件,可求12个纸箱转化成木箱的个数,先求出每个木箱装多少双,再求每个纸箱装多少双;答题：解：12个纸箱相当木箱的个数：2×12÷3=2×4＝8个一个木箱装鞋的双数：1800÷8+4=18000÷12=150双一个纸箱装鞋的双数：150×2÷3=100双答：每个纸箱可装鞋100双,每个木箱可装鞋150双18. 某工地运进一批沙子和水泥,运进沙子袋数是水泥的2倍;每天用去30袋水泥,40袋沙子,几天以后,水泥全部用完,而沙子还剩120袋,这批沙子和水泥各多少袋解题思路：由已知条件可知道,每天用去30袋水泥,同时用去30×2袋沙子,才能同时用完;但现在每天只用去40袋沙子,少用30×2-40袋,这样才累计出120袋沙子;因此看120袋里有多少个少用的沙子袋数,便可求出用的天数;进而可求出沙子和水泥的总袋数;答题：解：水泥用完的天数：120÷30×2-40=120÷20=6天水泥的总袋数：30×6=180袋沙子的总袋数：180×2=360袋答：运进水泥180袋,沙子360袋;19. 学校里买来了5个保温瓶和10个茶杯,共用了90元钱;每个保温瓶是每个茶杯价钱的4倍,每个保温瓶和每个茶杯各多少元解题思路：根据每个保温瓶的价钱是每个茶杯的4倍,可把5个保温瓶的价钱转化为20个茶杯的价钱;这样就可把5个保温瓶和10个茶杯共用的90元钱,看作30个茶杯共用的钱数;答题：解：每个茶杯的价钱：90÷4×5+10=3元每个保温瓶的价钱：3×4=12元答：每个保温瓶12元,每个茶杯3元;20. 两个数的和是572,其中一个加数个位上是0,去掉0后,就与第二个加数相同;这两个数分别是多少解题思路：已知一个加数个位上是0,去掉0,就与第二个加数相同,可知第一个加数是第二个加数的10倍,那么两个加数的和572,就是第二个加数的10＋1倍;答题：解：第一个加数：572÷10+1=52第二个加数：52×10=520答：这两个加数分别是52和520;21. 一桶油连桶重16千克,用去一半后,连桶重9千克,桶重多少千克解题思路：由已知条件可知,16千克和9千克的差正好是半桶油的重量;9千克是半桶油和桶的重量,去掉半桶油的重量就是桶的重量;答题：解：9-16-9=9-7=2千克答：桶重2千克;22. 一桶油连桶重10千克,倒出一半后,连桶还重5.5千克,原来有油多少千克解题思路：由已知条件可知,10千克与5.5千克的差正好是半桶油的重量,再乘以2就是原来油的重量;答题：解：10-5.5×2=9千克答：原来有油9千克;23. 用一只水桶装水,把水加到原来的2倍,连桶重10千克,如果把水加到原来的5倍,连桶重22千克;桶里原有水多少千克解题思路：由已知条件可知,桶里原有水的5-2倍正好是22-10千克,由此可求出桶里原有水的重量;答题：解：22-10÷5-2=12÷3=4千克答：桶里原有水4千克;24. 小红和小华共有故事书36本;如果小红给小华5本,两人故事书的本数就相等,原来小红和小华各有多少本解题思路：从“小红给小华5本,两人故事书的本数就相等”这一条件,可知小红比小华多5×2本书,用共有的36本去掉小红比小华多的本数,剩下的本数正好是小华本数的2倍;答题：解：小华有书的本数：36-5×2÷2=13本小红有书的本数：13+5×2=23本答：原来小红有23本,小华有13本;25. 有5桶油重量相等,如果从每只桶里取出15千克,则5只桶里所剩下油的重量正好等于原来2桶油的重量;原来每桶油重多少千克解题思路：由已知条件知,5桶油共取出15×5千克;由于剩下油的重量正好等于原来2桶油的重量,可以推出5-2桶油的重量是15×5千克;答题：解：15×5÷5-2=25千克答：原来每桶油重25千克;26. 把一根木料锯成3段需要9分钟,那么用同样的速度把这根木料锯成5段,需要多少分解题思路：把一根木料锯成3段,只锯出了3-1个锯口,这样就可以求出锯出每个锯口所需要的时间,进一步即可以求出锯成5段所需的时间;答题：解：9÷3-1×5-1=18分答：锯成5段需要18分钟;27. 一个车间,女工比男工少35人,男、女工各调出17人后,男工人数是女工人数的2倍;原有男工多少人女工多少人解题思路：女工比男工少35人,男、女工各调出17人后,女工仍比男工少35人;这时男工人数是女工人数的2倍,也就是说少的35人是女工人数的2-1倍;这样就可求出现在女工多少人,然后再分别求出男、女工原来各多少人;答题：解：35÷2-1=35人女工原有：35+17=52人男工原有：52+35=87人答：原有男工87人,女工52人;28. 李强骑自行车从甲地到乙地,每小时行12千米,5小时到达,从乙地返回甲地时因逆风多用1小时,返回时平均每小时行多少千米解题思路：由每小时行12千米,5小时到达可求出两地的路程,即返回时所行的路程;由去时5小时到达和返回时多用1小时,可求出返回时所用时间;答题：解：12×5÷5+1=10千米答：返回时平均每小时行10千米;29. 甲、乙二人同时从相距18千米的两地相对而行,甲每小时行走5千米,乙每小时走4千米;如果甲带了一只狗与甲同时出发,狗以每小时8千米的速度向乙跑去,遇到乙立即回头向甲跑去,遇到甲又回头向飞跑去,这样二人相遇时,狗跑了多少千米解题思路：由题意知,狗跑的时间正好是二人的相遇时间,又知狗的速度,这样就可求出狗跑了多少千米;答题：解：18÷5+4=2小时8×2=16千米答：狗跑了16千米;30. 有红、黄、白三种颜色的球,红球和黄球一共有21个,黄球和白球一共有20个,红球和白球一共有19个;三种球各有多少个解题思路：由条件知,21+20+19表示三种球总个数的2倍,由此可求出三种球的总个数,再根据题目中的条件就可以求出三种球各多少个;答题：解：总个数：21+20+19÷2=30个白球：30-21=9个红球：30-20=10个黄球：30-19=11个答：白球有9个,红球有10个,黄球有11个;31. 在一根粗钢管上接细钢管;如果接2根细钢管共长18米,如果接5根细钢管共长33米;一根粗钢管和一根细钢管各长多少米解题思路：根据题意,33米比18米长的米数正好是3根细钢管的长度,由此可求出一根细钢管的长度,然后求一根粗钢管的长度;答题：解：33-18÷5-2=5米18-5×2=8米答：一根粗钢管长8米,一根细钢管长5米;32. 水泥厂原计划12天完成一项任务,由于每天多生产水泥4.8吨,结果10天就完成了任务,原计划每天生产水泥多少吨解题思路：由题意知,实际10天比原计划10天多生产水泥4.8×10吨,而多生产的这些水泥按原计划还需用12-10天才能完成,也就是说原计划12-10天能生产水泥4.8×10吨;答题：解：4.8×10÷12-10=24吨答：原计划每天生产水泥24吨;33. 学校举办歌舞晚会,共有80人参加了表演;其中唱歌的有70人,跳舞的有30人,既唱歌又跳舞的有多少人解题思路：由题意知,实际10天比原计划10天多生产水泥4.8×10吨,而多生产的这些水泥按原计划还需用12-10天才能完成,也就是说原计划12-10天能生产水泥4.8×10吨;答题：解：4.8×10÷12-10=24吨答：原计划每天生产水泥24吨;34. 学校举办语文、数学双科竞赛,三年级一班有59人,参加语文竞赛的有36人,参加数学竞赛的有38人,一科也没参加的有5人;双科都参加的有多少人解题思路：参加语文竞赛的36人中有参加数学竞赛的,同样参加数学竞赛的38人中也有参加语文竞赛的,如果把两者加起来,那么既参加语文竞赛又参加数学竞赛的人数就统计了两次,所以将参加语文竞赛的人数加上参加数学竞赛的人数再加上一科也没参加的人数减去全班人数就是双科都参加的人数;答题：解：36+38+5-59=20人答：双科都参加的有20人;35. 学校买了4张桌子和6把椅子,共用640元;2张桌子和5把椅子的价钱相等,桌子和椅子的单价各是多少元解题思路：由“2张桌子和5把椅子的价钱相等”这一条件,可以推出4张桌子就相当于10把椅子的价钱,买4张桌子和6把椅子共用640元,也就相当于买16把椅子共用640元;答题：解：5×4÷2+6=16把640÷16=40元40×5÷2=10O元答：桌子和椅子的单价分别是100元、40元;36. 父亲今年45岁,5年前父亲的年龄是儿子的4倍,今年儿子多少岁解题思路：5年前父亲的年龄是45-5岁,儿子的年龄是45-5÷4岁,再加上5就是今年儿子的年龄;答题：解：45-5÷4+5 =10+5 =15岁答：今年儿子15岁;37. 有两桶油,甲桶油重是乙桶油重的4倍,如果从甲桶倒入乙桶18千克,两桶油就一样重,原来每桶各有多少千克油解题思路：“如果从甲桶倒入乙桶18千克,两桶油就一样重”可推出：甲桶油的重量比乙桶多18×2千克,又知“甲桶油重是乙桶油重的4倍”,可知18×2千克正好是乙桶油重量的4-1倍;答题：解：18×2÷4-1=12千克12×4=48千克答：原来甲桶有油48千克,乙桶有油12千克;38. 光明小学举办数学知识竞赛,一共20题;答对一题得5分,答错一题扣3分,不答得0分;小丽得了79分,她答对几道,答错几道,有几题没答解题思路：根据题意,20题全部答对得100分,答错一题将失去5+3分,而不答仅失去5分;小丽共失去100-79分;再根据100-79÷8=2题……5分,分析答对、答错和没答的题数;答题：解：5×20-75÷8=2题……5分20-2-1=17题答：答对17题,答错2题,有1题没答;39. 光明小学举办数学知识竞赛,一共20题;答对一题得5分,答错一题扣3分,不答得0分;小丽得了79分,她答对几道,答错几道,有几题没答解题思路：“从两车头相遇到两车尾相离”,两车所行的路程是两车身长之和,即240+264米,速度之和为20+16米;根据路程、速度和时间的关系,就可求得所需时间;答题：解：240+264÷20+16=504÷30 =14秒答：从两车头相遇到两车尾相离,需要14秒;40. 一列火车长600米,通过一条长1150米的隧道,已知火车的速度是每分700米,问火车通过隧道需要几分解题思路：火车通过隧道是指从车头进入隧道到车尾离开隧道,所行的路程正好是车身与隧道长度之和;答题：解：600+1150÷700 =1750÷700 =2.5分答：火车通过隧道需2.5分;41.小明从家里到学校,如果每分走50米,则正好到上课时间；如果每分走60米,则离上课时间还有2分;问小明从家里到学校有多远解题思路：在每分走50米的到校时间内按两种速度走,相差的路程是60×2米,又知每秒相差60-50米,这就可求出小明按每分50米的到校时间;答题：解：60×2÷60-50=12分50×12=600米答：小明从家里到学校是600米;42.有一周长600米的环形跑道,甲、乙二人同时、同地、同向而行,甲每分钟跑300米,乙每分钟跑400米,经过几分钟二人第一次相遇解题思路：由已知条件可知,二人第一次相遇时,乙比甲多跑一周,即600米,又知乙每分钟比甲多跑400-300米,即可求第一次相遇时经过的时间;答题：解：600÷400-300=600÷100 =6分答：经过6分钟两人第一次相遇43.有一个长方形纸板,如果只把长增加2厘米,面积就增加8平方米；如果只把宽增加2厘米,面积就增加12平方厘米;这个长方形纸板原来的面积是多少解题思路：由“只把宽增加2厘米,面积就增加12平方厘米”,可求出原来的长是：12÷2厘米,同理原来的宽就是8÷2厘米,求出长和宽,就能求出原来的面积;答题：解：12÷2×8÷2=24平方厘米答：这个长方形纸板原来的面积是24平方厘米;44.妈妈买苹果和梨各3千克,付出20元找回7.4元;每千克苹果2.4元,每千克梨多少元解题思路：用去的钱数除以3就是1千克苹果和1千克梨的总钱数;从这个总钱数里去掉1千克苹果的钱数,就是每千克梨的钱数;答题：解：20-7.4÷3-2.4 =12.6÷3-2.4 =4.2-2.4 =1.8元答：每千克梨1.8元;45.甲乙两人同时从相距135千米的两地相对而行,经过3小时相遇;甲的速度是乙的2倍,甲乙两人每小时各行多少千米解题思路：由题意知,甲乙速度和是135÷3千米,这个速度和是乙的速度的2+1倍;答题：解：135÷3÷2+1=15千米15×2=30千米答：甲乙每小时分别行30千米、15千米;46.盒子里有同样数目的黑球和白球;每次取出8个黑球和5个白球,取出几次以后,黑球没有了,白球还剩12个;一共取了几次盒子里共有多少个球解题思路：两种球的数目相等,黑球取完时,白球还剩12个,说明黑球多取了12个,而每次多取8-5个,可求出一共取了几次;答题：解：12÷8-5=4次8×4+5×4+12=64个或8×4×2=64个答：一共取了4次,盒子里共有64个球;47.上午6时从汽车站同时发出1路和2路公共汽车,1路车每隔12分钟发一次,2路车每隔18分钟发一次,求下次同时发车时间;解题思路：1路和2路下次同时发车时,所经过的时间必须既是12分的倍数,又是18分的倍数;也就是它们的最小公倍数;答题：解：12和18的最小公倍数是36。

小学六年级数学找规律练习题小学六年级数学找规律练习题11、一座拱形桥的两根望柱间隔1米，每侧各有15根望柱，这座拱形桥长几米?2、四年级一班有60人，排成两队，每两个同学相隔1米，队伍前后长几米?3、公园圆形草坪四周有10个小喷水池，每两个喷水池中间有2把休息椅。

你明白一共有几把休息椅吗?4、张强家住在6楼，从1楼到3楼需要走34级台阶。

假如各层楼台阶数相同，张强到家需要走多少级台阶?5、在一条路的两边装路灯，每隔15米装一盏。

假如路的两端都要装，一共需要装162盏。

这条路全长多少米?6、在一条公路的两侧栽树，每隔5米栽一棵，公路的两端都有树，公路长400米，公路每侧要植几棵树?两侧一共要植几棵树?7、张老师要沿200米圆形跑道每隔5米插一面彩旗，一共需要几面彩旗?8、在一张边长为3米的方桌周围摆水果，每个角上都要摆一盘。

假如每隔1米摆一盘，这张方桌上能摆几盘水果?每条边上有几盘?9、学校林荫路长54米，路的一边从一端到另一端一共栽了19棵树，每两棵树之间相距几米?10、为美化环境，园林公司在草坪的一侧每隔2米摆了一盆花，两端都摆共摆了56盆花，现在全部换成木桩做成护拦，这一侧共用了111根木桩，相邻两根木桩间相距几米?11、某人到高层建筑的10层去，他从1层到5层用了100秒，假如用同样的速度走到10层，还需要多少秒?12、科学家进行一项实验，每隔5小时做一次记录。

做第12次记录时，挂钟的时针正好指向9，问做第一次记录时，时针指向几?13、两棵树相隔115米，中间以相等距离增加22棵后，第16棵与第1棵之间相隔几米?14、有一条植着等距离树的路，哥哥和弟弟同时动身，从第一棵数到最后一棵树方向走去，哥哥每分钟走84米，弟弟每分钟走36米。

哥哥走到第22棵树时，弟弟走到第几棵树?15、一列火车共20节，每节长5米，每两节之间相距1米，这列火车以每分钟20米的速度通过81米长的隧道，需要几分钟?16、请你把9棵树平均栽成8行，每行栽3棵，你能否做到?假如能请画出栽树的示意图。

小学六年级找规律练习题小学六年级找规律练习题在小学数学学习中，找规律是一个重要的能力。

通过找规律，我们可以发现数列中的规律，进而解决一些数学问题。

下面，我将为大家提供一些小学六年级找规律的练习题，希望能够帮助大家提高这一能力。

1. 数字序列：2, 4, 6, 8, 10, ...规律：每个数字都比前一个数字大2。

下一个数字是多少？2. 数字序列：3, 6, 9, 12, 15, ...规律：每个数字都比前一个数字大3。

下一个数字是多少？3. 数字序列：1, 4, 9, 16, 25, ...规律：每个数字都是前一个数字的平方。

下一个数字是多少？4. 数字序列：1, 3, 6, 10, 15, ...规律：每个数字都比前一个数字多1、2、3、4、5...下一个数字是多少？5. 数字序列：1, 4, 9, 16, 25, ...规律：每个数字都是从1开始的连续奇数的平方。

下一个数字是多少？6. 数字序列：1, 3, 6, 10, 15, ...规律：每个数字都是从1开始的连续自然数的累加和。

下一个数字是多少？通过以上的练习题，我们可以看到找规律的方法有很多种。

在解决这些题目时，我们可以通过观察数字之间的差异，或者是数字之间的倍数关系来找到规律。

除了以上的练习题，我们还可以通过一些游戏来锻炼找规律的能力。

例如，我们可以给出一组数字，要求孩子们找出其中的规律，并继续往下延伸。

这样的游戏不仅能够提高孩子们的观察力和逻辑思维能力，还能够培养他们的耐心和坚持不懈的品质。

找规律不仅仅是数学学习中的一种技能，它还贯穿于我们日常生活的方方面面。

例如，我们可以通过找规律来解决一些生活中的问题，比如整理书桌时，我们可以找到一种规律来摆放书籍，使得整个书桌看起来更加整洁有序。

通过找规律的练习，我们可以培养孩子们的观察力、逻辑思维能力和解决问题的能力。

这些能力不仅在数学学习中有用，还能够在其他学科和生活中发挥作用。

因此，我们应该多给孩子们提供找规律的机会，让他们在实践中不断提高。

六年级找规律数学题一、数字规律1. 按规律填数：1，3，6，10，15，（），28。

- 解析：观察这组数字，1到3增加了2，3到6增加了3，6到10增加了4，10到15增加了5。

可以发现相邻两个数的差值在依次递增1。

那么15后面的数应该比15大6，即15 + 6 = 21。

验证一下，21到28增加了7，符合规律。

所以括号里应填21。

2. 数列：2，4，8，16，32，（）。

- 解析：这组数列中，2×2 = 4，4×2 = 8，8×2 = 16，16×2 = 32。

可以得出规律是后一个数是前一个数的2倍。

所以括号里的数应该是32×2 = 64。

二、图形规律1. 用小棒按照如下方式摆三角形：摆1个三角形需要3根小棒；摆2个三角形需要5根小棒；摆3个三角形需要7根小棒……（1）摆10个三角形需要多少根小棒？- 解析：观察可得，摆1个三角形用3根小棒（3 = 2×1+1）；摆2个三角形用5根小棒（5 = 2×2 + 1）；摆3个三角形用7根小棒（7 = 2×3+1）。

可以总结出规律，摆n个三角形需要2n + 1根小棒。

当n = 10时，2×10+1 = 21根小棒。

（2）有21根小棒，可以摆多少个三角形？- 解析：根据前面总结的规律2n+1。

设可以摆n个三角形，则2n + 1 = 21，2n = 20，解得n = 10。

所以21根小棒可以摆10个三角形。

2. 下列图形是由同样大小的小圆圈按照一定规律所组成的，其中第1个图形中一共有6个小圆圈，第2个图形中一共有9个小圆圈，第3个图形中一共有12个小圆圈……（1）第5个图形中有多少个小圆圈？- 解析：观察图形，第1个图形有6 = 3×1+3个小圆圈；第2个图形有9 = 3×2 + 3个小圆圈；第3个图形有12 = 3×3+3个小圆圈。

可以得出规律，第n个图形有3n+3个小圆圈。

六年级数学上册综合算式练习题找规律综合算式题是数学学习中的重要部分，通过解答这类题目，可以帮助学生培养逻辑思维和问题解决能力。

在六年级数学上册的学习中，综合算式练习题也占有一定的比例。

本文将通过找规律的方法，给出一些六年级数学上册综合算式练习题的解答方法。

1. 一家餐厅一天的雇佣费用是1000元，每天雇佣3个厨师和5个服务员。

如果厨师的日薪是150元，服务员的日薪是100元，那么这家餐厅一天的雇佣费用是多少？解答：我们可以先计算出一天雇佣厨师和服务员的费用，然后求和。

厨师的费用为3个厨师 × 150元/人 × 1天 = 450元；服务员的费用为5个服务员 × 100元/人 × 1天 = 500元。

最后，将两者相加，即可得出答案：450元 + 500元 = 950元。

2. 某超市购进了一批商品，每件商品进货价为100元，每件商品标价为150元。

如果超市卖出了这批商品的60%，那么超市的总利润是多少？解答：首先，我们可以计算出每件商品的利润，即标价减去进货价，即150元 - 100元 = 50元。

然后，我们计算出这批商品的总利润，即每件商品利润乘以卖出数量的百分比，即50元 × 60% = 30元。

所以，超市的总利润为30元。

3. 某学校举行了一次运动会，共有600名学生参加比赛。

学校为参赛学生提供了午餐，每人的午餐费用为8元。

学校总共花费了2400元，请问参加比赛的学生有多少人？解答：我们可以通过除法来得到答案。

学校花费的总金额2400元除以每人的午餐费用8元，即2400元 ÷ 8元/人 = 300人。

所以，参加比赛的学生共有300人。

4. 小明和小红从同一地点同时出发，相同的速度向同一方向行走。

小明走了8千米后，小红才走了5千米。

如果小红走了18千米后，小明走了多少千米？解答：我们可以通过比例的方法来求解。

小明走了8千米，小红才走了5千米，可以得到比例为8:5。

一、选择题（每题2分，共10分）1. 下面哪组数列是按照一定规律排列的？A. 2, 4, 6, 8, 10, 12, ...B. 3, 6, 9, 12, 15, 18, ...C. 1, 3, 6, 10, 15, 21, ...D. 4, 8, 12, 16, 20, 24, ...2. 下列哪个数不是3的倍数？A. 12B. 15C. 18D. 213. 下列哪个图形不是按照一定规律排列的？A. 正方形、长方形、正方形、长方形、正方形、长方形B. 三角形、正方形、五边形、正方形、五边形、正方形C. 圆形、长方形、圆形、长方形、圆形、长方形D. 正方形、正方形、正方形、正方形、正方形、正方形4. 下面哪个数列是按照等差数列排列的？A. 2, 4, 6, 8, 10, 12, ...B. 1, 3, 5, 7, 9, 11, ...C. 2, 5, 8, 11, 14, 17, ...D. 3, 6, 9, 12, 15, 18, ...5. 下列哪个数列是按照等比数列排列的？A. 2, 4, 8, 16, 32, 64, ...B. 1, 2, 4, 8, 16, 32, ...C. 3, 6, 12, 24, 48, 96, ...D. 4, 8, 12, 16, 20, 24, ...二、填空题（每题2分，共10分）6. 数列：1, 3, 5, 7, ...，下一个数是______。

7. 数列：2, 6, 18, 54, ...，下一个数是______。

8. 数列：1, 4, 9, 16, ...，下一个数是______。

9. 数列：2, 5, 10, 17, ...，下一个数是______。

10. 数列：1, 2, 4, 8, 16, ...，下一个数是______。

三、解答题（每题10分，共30分）11. 小明从1楼开始，每次上2楼，请问第10次上楼时，小明在几楼？12. 小红有一堆苹果，她每次拿出其中的1/3，问她第3次拿出苹果后，还剩下多少苹果？13. 一个数列的前三项分别是1, 4, 7，请找出这个数列的规律，并写出第10项。