结构力学 第二章 几何组成分析(典型例题)

第二章 结构的几何组成分析（一）单项选择题1．三刚片组成无多余约束的几何不变体系，其连接方式是 【 B 】A ．以任意的三个铰相连B ．以不在一条线上的三个铰相连C ．以三对平行链杆相连D ．以三个无穷远处的虚铰相连2．从一个无多余约束几何不变体系上去除二元体得到的新体系为 【 A 】 A ．无多余约束的几何不变体系 B ．有多余约束的几何不变体系 C ．常变体系 D ．瞬变体系 3．静定结构的几何组成是【 C 】A ．瞬变体系B ．常变体系C ．无多余约束的几何不变体系D ．有多余约束的几何不变体系 4．图示体系属于【 D 】A ．无多余约束的几何不变体系B ．有多余约束的几何不变体系C ．瞬变体系D ．常变体系5．图示体系是【 B 】A ．瞬变体系B ．常变体系C ．无多余约束的几何不变体系D ．有多余约束的几何不变体系 （二）填空题6．连接4个刚片的复铰相当于 6 个约束。

7．不能起到减少自由度作用的约束称为 多余约束 。

8．将三刚片组成无多余约束的几何不变体系，必要的约束数目是 6 。

9．在一个几何不变体系上加二元体后的新体系为 几何不变体系 。

10．图示体系的几何组成是 无多与约束的几何不变体系 。

（三）分析题11～15．对图示体系进行几何组成分析（要写出分析过程）。

题4图题5图题10图解：11．撤除支座约束，剩余部分为刚片Ⅰ和Ⅱ用既不完全平行又不完全相交的三根链杆1、2、3相连，故原体系为无多余约束的几何不变体系12题解：．撤除支座约束，去除二元体C -A -D 、C -B -E ，剩余部分为刚片Ⅰ(CDE )和Ⅱ(FGH )用既不完全平行又不完全相交的三根链杆1、2、3相连，故原体系为无多余约束的几何不变体系。

AB C DEF GH题12图AB CDE FC D E F 答11图 ⅠⅡ 1 2 3 D E F GH答12图 12313题解；．撤除支座约束，去除二元体D -C -E ，剩余部分为两刚片（杆AF 和BF ）用两平行链杆相连，故原体系为有一个自由度的几何可变体系。

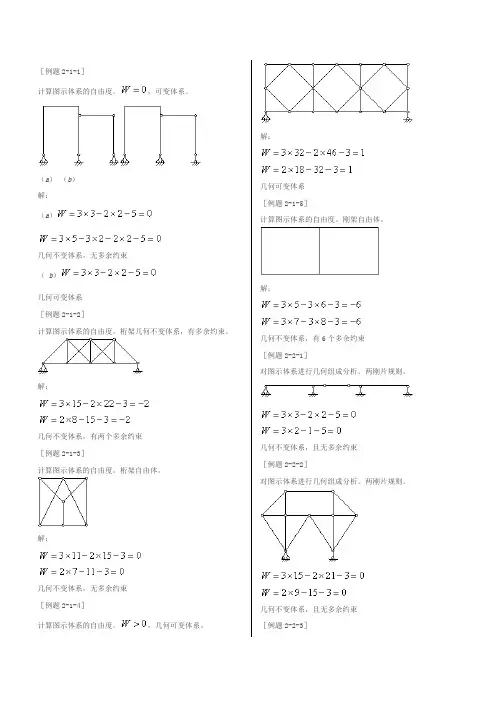
［例题2-1-1］计算图示体系的自由度。

，可变体系。

（a）（b）解：（a ）几何不变体系，无多余约束（b ）几何可变体系［例题2-1-2］计算图示体系的自由度。

桁架几何不变体系，有多余约束。

解：几何不变体系，有两个多余约束［例题2-1-3］计算图示体系的自由度。

桁架自由体。

解：几何不变体系，无多余约束［例题2-1-4］计算图示体系的自由度。

，几何可变体系。

解：几何可变体系［例题2-1-5］计算图示体系的自由度。

刚架自由体。

解：几何不变体系，有6个多余约束［例题2-2-1］对图示体系进行几何组成分析。

两刚片规则。

几何不变体系，且无多余约束［例题2-2-2］对图示体系进行几何组成分析。

两刚片规则。

几何不变体系，且无多余约束［例题2-2-3］对图示体系进行几何组成分析。

两刚片规则。

几何不变体系，且无多余约束 ［例题2-2-4］对图示体系进行几何组成分析。

两刚片规则。

几何不变体系，有一个多余约束 ［例题2-2-5］对图示体系进行几何组成分析。

二元体规则。

几何不变体系，且无多余约束 ［例题2-2-6］对图示体系进行几何组成分析。

两刚片规则，三刚片规则。

几何不变体系，且无多余约束 ［例题2-2-7］对图示体系进行几何组成分析。

三刚片规则。

几何不变体系，且无多余约束 ［例题2-2-8］对图示体系进行几何组成分析。

三刚片规则。

几何不变体系，且无多余约束 ［例题2-3-1］对图示体系进行几何组成分析。

两刚片规则。

几何瞬变体系 ［例题2-3-2］对图示体系进行几何组成分析。

两刚片规则。

几何瞬变体系 ［例题2-3-3］对图示体系进行几何组成分析。

三刚片规则。

几何瞬变体系 ［例题2-3-4］对图示体系进行几何组成分析。

三刚片规则。

几何不变体系，且无多余约束 ［例题2-3-5］对图示体系进行几何组成分析。

三刚片规则。

几何不变体系，且无多余约束 ［例题2-3-6］对图示体系进行几何组成分析。

二元体规则，三刚片规则。

几何瞬变体系 ［例题2-3-7］对图示体系进行几何组成分析。

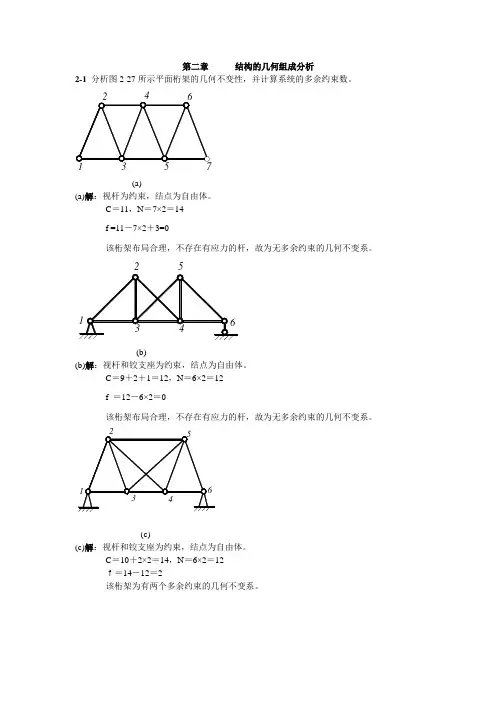
第二章 结构的几何组成分析2-1 分析图2-27所示平面桁架的几何不变性，并计算系统的多余约束数。

3571(a)(a)解：视杆为约束，结点为自由体。

C ＝11，N ＝7×2＝14f =11－7×2＋3=0该桁架布局合理，不存在有应力的杆，故为无多余约束的几何不变系。

(b)(b)解：视杆和铰支座为约束，结点为自由体。

C ＝9＋2＋1＝12，N ＝6×2＝12f ＝12－6×2＝0该桁架布局合理，不存在有应力的杆，故为无多余约束的几何不变系。

(c)(c)解：视杆和铰支座为约束，结点为自由体。

C ＝10＋2×2＝14，N ＝6×2＝12ｆ＝14－12＝2该桁架为有两个多余约束的几何不变系。

1217(d)(d)解：视杆和铰支座为约束，结点为自由体。

C ＝30＋3＝33，N ＝17×2＝34ｆ＝33－34＝-1故该桁架为几何可变系。

8(e)(e)解：视杆为约束，结点为自由体。

C ＝13，N ＝8×2＝16ｆ＝13－16＋3＝0将1-2-3-4、5-6-7-8看作两刚片，杆3-6、杆2-7、杆4-5相互平行，由两刚片原则知，为瞬时可变系统。

6(f)(f)解：视杆和固定铰支座为约束，结点为自由体。

C ＝22＋3×2＝28，N ＝14×2＝28ｆ＝28－28＝0将12-13-14、7-11-12、1-2-3-4-5-6-7-8-9-10看作三刚片，三刚片由铰7、铰12、铰14连结，三铰共线，故该桁架为瞬时可变系统。

(g)(g)解：视杆和固定铰支座为约束，结点为自由体。

C＝24＋4×2＝32，N＝16×2＝32ｆ＝32－32＝0由于杆15-14-3、杆12-11-4、杆9-5相交于一点，故该桁架为瞬时可变系。

(h)(h)解：视杆和固定铰支座为约束，结点为自由体。

C＝12＋2×2＝16，N＝8×2＝16ｆ＝16－16＝0该桁架布局合理，加减二元体之后，无有应力的杆，故该桁架为无多余约束的几何不变系。

第1章 绪论（无习题）第2章 平面体系的几何组成分析习题解答习题2.1 是非判断题(1) 若平面体系的实际自由度为零，则该体系一定为几何不变体系。

( )(2) 若平面体系的计算自由度W =0，则该体系一定为无多余约束的几何不变体系。

( ) (3) 若平面体系的计算自由度W ＜0，则该体系为有多余约束的几何不变体系。

( ) (4) 由三个铰两两相连的三刚片组成几何不变体系且无多余约束。

( )(5) 习题2.1(5) 图所示体系去掉二元体CEF 后，剩余部分为简支刚架，所以原体系为无多余约束的几何不变体系。

( )B DACEF习题 2.1(5)图(6) 习题2.1(6)(a)图所示体系去掉二元体ABC 后，成为习题2.1(6) (b)图，故原体系是几何可变体系。

( )(7) 习题2.1(6)(a)图所示体系去掉二元体EDF 后，成为习题2.1(6) (c)图，故原体系是几何可变体系。

()(a)(b)(c)AEBFCD习题 2.1(6)图【解】（1）正确。

（2）错误。

0W 是使体系成为几何不变的必要条件而非充分条件。

（3）错误。

（4）错误。

只有当三个铰不共线时，该题的结论才是正确的。

（5）错误。

CEF 不是二元体。

（6）错误。

ABC 不是二元体。

（7）错误。

EDF 不是二元体。

习题2.2 填空(1) 习题2.2(1)图所示体系为_________体系。

习题2.2(1)图(2) 习题2.2(2)图所示体系为__________体系。

习题2-2(2)图(3) 习题 2.2(3)图所示4个体系的多余约束数目分别为_______、________、__________、__________。

习题2.2(3)图(4) 习题2.2(4)图所示体系的多余约束个数为___________。

习题2.2(4)图(5) 习题2.2(5)图所示体系的多余约束个数为___________。

习题2.2(5)图(6) 习题2.2(6)图所示体系为_________体系，有_________个多余约束。

结构力学习题第2章平面体系的几何组成分析2-1～2-6 试确定图示体系的计算自由度。

题2-1图题2-2图题2-3图题2-4图题2-5图题2-6图2-7～2-15 试对图示体系进行几何组成分析。

若是具有多余约束的几何不变体系，则需指明多余约束的数目。

题2-7图题2-8图题2-9图题2-10图题2-11图题2-12图题2-13图题2-14图题2-15图题2-16图题2-17图题2-18图题2-19图题2-20图题2-21图2-1 1W=2-1 9-W=2-3 3-W=2-4 2-W=2-5 1-W=2-6 4-W=2-7、2-8、2-12、2-16、2-17无多余约束的几何不变体系2-9、2-10、2-15具有一个多余约束的几何不变体系2-11具有六个多余约束的几何不变体系2-13、2-14几何可变体系为2-18、2-19 瞬变体系2-20、2-21具有三个多余约束的几何不变体系第3章静定梁和静定平面刚架的内力分析3-1 试作图示静定梁的内力图。

（a）（b）(c) (d)习题3-1图3-2 试作图示多跨静定梁的内力图。

（a）（b）(c)习题3-2图3-3～3-9 试作图示静定刚架的内力图。

习题3-3图习题3-4图习题3-5图习题3-6图习题3-7图习题3-8图习题3-9图3-10 试判断图示静定结构的弯矩图是否正确。

(a)(b)(c)(d)部分习题答案3-1 （a ）m kN M B ⋅=80（上侧受拉），kN F RQB 60=，kN F L QB 60-=（b ）m kN M A ⋅=20（上侧受拉），m kN M B ⋅=40（上侧受拉），kN F RQA 5.32=，kN F L QA 20-=，kN F LQB 5.47-=，kN F R QB 20=(c) 4Fl M C =（下侧受拉），θcos 2F F L QC =3-2 (a) 0=E M ，m kN M F ⋅-=40（上侧受拉），m kN M B ⋅-=120（上侧受拉）（b ）m kN M RH ⋅-=15(上侧受拉)，m kN M E ⋅=25.11（下侧受拉）（c ）m kN M G ⋅=29(下侧受拉)，m kN M D ⋅-=5.8(上侧受拉)，m kN M H ⋅=15(下侧受拉) 3-3 m kN M CB ⋅=10（左侧受拉），m kN M DF ⋅=8（上侧受拉），m kN M DE ⋅=20（右侧受拉） 3-4 m kN M BA ⋅=120（左侧受拉）3-5 m kN M F ⋅=40（左侧受拉），m kN M DC ⋅=160（上侧受拉），m kN M EB ⋅=80(右侧受拉) 3-6 m kN M BA ⋅=60（右侧受拉），m kN M BD ⋅=45（上侧受拉），kN F QBD 46.28=3-7 m kN M C ⋅=70下（左侧受拉），m kN M DE ⋅=150（上侧受拉），m kN M EB ⋅=70(右侧受拉) 3-8 m kN M CB ⋅=36.0（上侧受拉），m kN M BA ⋅=36.0（右侧受拉） 3-9 m kN M AB ⋅=10（左侧受拉），m kN M BC ⋅=10（上侧受拉） 3-10 （a ）错误 （b ）错误 （c ）错误 （d ）正确第4章 静定平面桁架和组合结构的内力分析4-1 试判别习题4-1图所示桁架中的零杆。

第二章结构的几何组成分析2-1分析图2-27所示平面桁架的几何不变性，并计算系统的多余约束数。

(a)(a)解：视杆为约束，结点为自由体。

C＝11，N＝7×2＝14f =11－7×2＋3=0该桁架布局合理，不存在有应力的杆，故为无多余约束的几何不变系。

(b)(b)解：视杆和铰支座为约束，结点为自由体。

C＝9＋2＋1＝12，N＝6×2＝12f ＝12－6×2＝0该桁架布局合理，不存在有应力的杆，故为无多余约束的几何不变系。

(c)(c)解：视杆和铰支座为约束，结点为自由体。

C＝10＋2×2＝14，N＝6×2＝12ｆ＝14－12＝2该桁架为有两个多余约束的几何不变系。

1217(d)(d)解：视杆和铰支座为约束，结点为自由体。

C ＝30＋3＝33，N ＝17×2＝34ｆ＝33－34＝-1故该桁架为几何可变系。

(e)(e)解：视杆为约束，结点为自由体。

C ＝13，N ＝8×2＝16ｆ＝13－16＋3＝0将1-2-3-4、5-6-7-8看作两刚片，杆3-6、杆2-7、杆4-5相互平行，由两刚片原则知，为瞬时可变系统。

6 (f)(f)解：视杆和固定铰支座为约束，结点为自由体。

C ＝22＋3×2＝28，N ＝14×2＝28ｆ＝28－28＝0将12-13-14、7-11-12、1-2-3-4-5-6-7-8-9-10看作三刚片，三刚片由铰7、铰12、铰14连结，三铰共线，故该桁架为瞬时可变系统。

(g)(g)解：视杆和固定铰支座为约束，结点为自由体。

C＝24＋4×2＝32，N＝16×2＝32ｆ＝32－32＝0由于杆15-14-3、杆12-11-4、杆9-5相交于一点，故该桁架为瞬时可变系。

(h)(h)解：视杆和固定铰支座为约束，结点为自由体。

C＝12＋2×2＝16，N＝8×2＝16ｆ＝16－16＝0该桁架布局合理，加减二元体之后，无有应力的杆，故该桁架为无多余约束的几何不变系。